《一元二次含绝对值的不等式的解法》图文课件
- 格式:ppt
- 大小:409.50 KB
- 文档页数:11

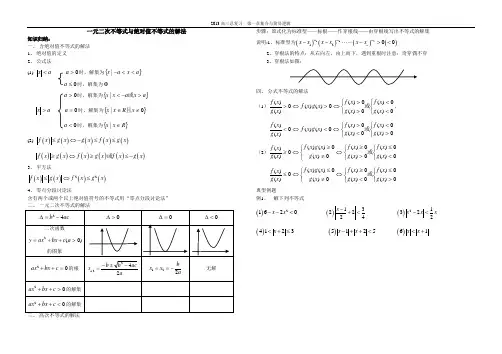
一元二次不等式与绝对值不等式的解法知识归纳: 一、 含绝对值不等式的解法 1、 绝对值的定义 2、 公式法(1) a x < 0>a 时,解集为{}axa x <<-|0≤a 时,解集为Φ0>a 时,解集为{}a x a x x >-<或|a x > 0=a 时,解集为{}0|≠∈x R x x 且0<a 时,解集为{}R x x ∈|(2) ()()()()()f x g x g x f x g x ≤⇔-≤≤ ()()()()()()fx g x f x g x f x gx≥⇔≥≤-或 3、 平方法()()()()22f x g x f x g x ≤⇔≤4、 零点分段讨论法含有两个或两个以上绝对值符号的不等式用“零点分段讨论法” 二、 一元二次不等式的解法三、 高次不等式的解法步骤:原式化为标准型——标根——作穿根线——由穿根线写出不等式的解集 说明:1、标准型为()()()()121200nm m m n x x x x x x --⋅⋅⋅⋅⋅⋅-><2、穿根法的特点:从右向左,由上而下,遇到重根时注意:奇穿偶不穿3、穿根法如图:四、 分式不等式的解法 (1)⎩⎨⎧<<⎩⎨⎧>>⇔>⇔>0)(0)(0)(0)(0)()(0)()(x g x f x g x f x g x f x g x f 或, ⎩⎨⎧><⎩⎨⎧<>⇔<⇔<0)(0)(0)(0)(0)()(0)()(x g x f x g x f x g x f x g x f 或 (2)⎩⎨⎧<≤⎩⎨⎧>≥⇔⎩⎨⎧≠≥⇔≥0)(0)(0)(0)(0)(0)()(0)()(x g x f x g x f x g x g x f x g x f 或 ⎩⎨⎧>≤⎩⎨⎧<≥⇔⎩⎨⎧≠≤⇔≤0)(0)(0)(0)(0)(0)()(0)()(x g x f x g x f x g x g x f x g x f 或 典型例题例1、 解下列不等式()21620x x --< ()132224x -+< ()21322x x x -< ()4123x <+≤ ()5125x x -++< ()61x x <+例2、 若不等式43x x a -+-<有解,则实数a 的取值范围是思维拓展:1、若不等式43x x a -+-<的解集是空集,则实数a 的取值范围是2、若不等式43x x a ---<的解集是空集,则实数a 的取值范围是例3、若12x <≤,不等式2210ax ax --<恒成立,求实数a 的取值范围例4、解下列关于x 的不等式()()212120ax a x -++< ()222150x x --≥ ()()()()225301x x x x --≥+⋅堂清练习 1、不等式130x x->的解集为( ) A. 110,,33⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭B. 11,0,33⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭C. 11,33⎛⎫- ⎪⎝⎭D. 1,3⎛⎫-∞- ⎪⎝⎭2、若不等式234x ->与不等式20x px q ++>的解集相同,则:p q 等于( )A. 12:7B. 7:12C. 12-:7D. 3-:4 3、若关于x 的不等式2122x x mx -+>的解集为{}|02x x <<,则实数m 的值为 4、不等式()()()2321103x x x x +-+≥-的解集是5、已知关于x 的不等式30ax b +>的解集为{}|1x x >,则不等式()()20a b x a b ++-<的解集为6、解不等式25123xx x -<---7、解关于x 的不等式()()22210x a x a a a R ++++>∈。



初高中衔接教材1、一元二次不等式解法二次函数y =x 2-x -6的对应值表与图象如下:x -3 -2 -1 0 1 2 3 4 y6-4-6-6-46由对应值表及函数图象(如图2.3-1)可知 一元二次方程x 2-x -6=0的解就是:同样,结合抛物线与x 轴的相关位置,可以得到 一元二次不等式x 2-x -6>0的解是一元二次不等式x 2-x -6<0的解是上例表明:由抛物线与x 轴的交点可以确定对应的一元二次方程的解和对应的一元二次不等式的解集.那么,怎样解一元二次不等式a x 2+bx +c >0(a ≠0)呢? 我们可以用类似于上面例子的方法,借助于二次函数y =ax 2+bx +c (a ≠0)的图象来解一元二次不等式ax2+bx +c >0(a ≠0). 为了方便起见,我们先来研究二次项系数a >0时的一元二次不等式的解.我们知道,对于一元二次方程ax 2+bx +c =0(a >0),设△=b 2-4ac ,它的解的情形按照△>0,△=0,△<0分别为下列三种情况——有两个不相等的实数解、有两个相等的实数解和没有实数解,相应地,抛物线y =ax 2+bx +c (a >0)与x 轴分别有两个公共点、一个公共点和没有公共点(如图2.3-2所示),因此,我们可以分下列三种情况讨论对应的一元二次不等式ax 2+bx +c >0(a >0)与ax 2+bx +c <0(a >0)的解. (1)当Δ>0时,抛物线y =ax 2+bx +c (a >0)与x 轴有两个公共点(x 1,0)和(x 2,0),xyO x 1 x 2xyO x 1= x 2yxO图2.3-2②③①方程ax2+bx +c =0有两个不相等的实数根x1和x 2(x 1<x 2),由图2.3-2①可知不等式ax 2+bx +c >0的解为:不等式ax 2+bx +c <0的解为:(2)当Δ=0时,抛物线y =ax 2+bx +c (a >0)与x 轴有且仅有一个公共点,方程ax2+bx +c =0有两个相等的实数根x 1=x 2=-b2a,由图2.3-2②可知不等式ax 2+bx +c >0的解为: 不等式ax 2+bx +c <0的解为: (3)如果△<0,抛物线y =ax 2+bx +c (a >0)与x 轴没有公共点,方程ax2+bx +c =0没有实数根,由图2.3-2③可知不等式ax 2+bx +c >0的解为: 不等式ax 2+bx +c <0的解为: 今后,我们在解一元二次不等式时,如果二次项系数大于零,可以利用上面的结论直接求解;如果二次项系数小于零,则可以先在不等式两边同乘以-1,将不等式变成二次项系数大于零的形式,再利用上面的结论去解不等式. 例1、 解不等式:(1)x 2+2x -3≤0; (2)x -x 2+6<0;(3)4x 2+4x +1≥0; (4)x 2-6x +9≤0;(5)-4+x -x 2<0.例2、 已知不等式20(0)ax bx c a ++<≠的解是求不2,3x x <>或等式20bx ax c ++>的解.例3、 解关于的一x 元二次不等式210(x ax a ++>为实数). 分析 对于一元二次不等式,按其一般解题步骤,首先应该将二次项系数变成正数,本题已满足这一要求,欲求一元二次不等式的解,要讨论根的判别式的符∆号,而这里的是∆关于未知系数的代数式, ∆的符号取决于未知系数的取值范围,因此,再根据解题的需要,对的符号进∆行分类讨论.例6 已知函数y=x2-2ax+1(a为常数)在-2≤x≤1上的最小值为n,试将n用a表示出来.分析:由该函数的图象可知,该函数的最小值与抛物线的对称轴的位置有关,于是需要对对称轴的位置进行分类讨论.练习1.解下列不等式:(1)3x2-x-4>0;(2)x2-x-12≤0;(3)x2+3x-4>0;(4)16-8x+x2≤0.2.解关于x的不等式x2+2x+1-a2≤0(a为常数).习题2A 组1.解下列不等式:(1)3x2-2x+1<0;(2)3x2-4<0;(3)2x-x2≥-1;(4)4-x2≤0.B 组 1.解关于x的不等式x2-(1+a)x+a<0(a为常数).C 组1.已知关于x不等式2x2+bx-c>0的解为x<-1,或x>3.试解关于x的不等式bx2+cx+4≥0.2.试求关于x 的函数y =-x 2+mx +2在0≤x ≤2上的最大值k .答案练 习2.(1)无解 (2)232333x -<<(3)1-2≤x ≤1+ 2 (4)x ≤-2,或x ≥2B 组1.不等式可变形为(x -1)(x -a )<0. ∴当a >1时,原不等式的解为1<x <a ; 当a =1时,原不等式的无实数解; 当a <1时,原不等式的解为a <x <1.C 组1.由题意,得 -1和3是方程2x 2+bx -c =0的两根,∴-1+3=-b 2 ,-1×3=-c2, 即b =-4,c =6.∴等式bx2+cx +4≥0就为-4 x 2+6x +4≥0,即2 x 2-3x -2≤0,∴-12≤x ≤2.2.∵y =-x 2+mx +2=-(x -m 2 )2+2+ m 24,∴当0≤m 2 ≤2,即0≤m ≤4时,k =2+ m 24 ;当m2 <0,即m <0时,k =2;当m2>2,即m >4时,k =2m -2.∴22,0,2,04,422,4.m mk m m m <⎧⎪⎪=+≤≤⎨⎪->⎪⎩2、含绝对值的不等式一【要点回顾】 1.绝对值[1]绝对值的代数意义: .即||a = .[2]绝对值的几何意义: 的距离. [3]两个数的差的绝对值的几何意义:a b -表示 的距离.二、讲解新课:1.)0(><a a x 与型的不等)0(>>a a x 式的解法先看含绝对值的方程|x|=2几何意义:数轴上表示数x 的点离开原点的距离等于2.∴x=±2提问:2<x 与的几何意2>x 义是什么?表示在数轴上应该是怎样的? 数轴上表示数x 的点离开原点的距离小(大)于2xO 2-2xO 2-2即 不等式 2<x 的解集是: 不等式 2>x 的解集是.:类似地,不等式)0(><a a x |与的几何意)0(>>a a x 义是什么?解集又是什么? 即 不等式的解)0(><a a x 集是: 不等式的解)0(>>a a x 集是:小结:①解法:利用绝对值几何意义 ②数形结合思想 2.c b ax <+,与型的不等)0(>>+c c b ax 式的解法把 b ax + 看作一个整体时,可化为与型)0(><a a x )0(>>a a x 的不等式来求解即 不等式的解)0(><+c c b ax 集为 : 不等式的解)0(>>+c c b ax 集为 : 三、讲解范例:例1、解不等式5500≤-x . 例2、解不等式752>+x .课内练习1.解不等式组⎩⎨⎧<->111x x 2.求使有意义4123-+-x x 的取值范围( )3.若则化简的313<-x 41291624922++++-x x x x 结果为例3解不等式 1≤ | 2x-1 | < 5. 练习:解下列不等式:7522≤-<x例2 解不等式:|4x-3|>2x+1.例3 解不等式:|x-3|-|x+1|<1. 练习:解不等式:| x+2 | + | x | >4.例4.解关于的不x 等式①)(R a a x ∈<,②)(R a a x ∈>例5.解关于的不x 等式)(132R a a x ∈<-+.练习: 1.解下列不等式:(1)7522≤-<x (2)1122+<-x x2.已知不等式a x ≤-2)0(>a 的解集为{}c x R x <<-∈1|,求c a 2+的值.3、 解下列不等式:(1)21x -< (2)13x x -+->4.(3)327x x ++-<。

含绝对值的不等式解法,一元二次不等式解法:|x|的几何意义是实数x在数轴上对应的点离开原点O的距离,所以|x|<a (a>0)的解集是{x|-a<x<a};不等式|x|>a (a>0)的解集是{x|x>a或x<-a}把不等式|x|<a与|x|>a (a>0)中的x替换成ax+b可以得到|ax+b|<c与|ax+b|>c (c>0)型的不等式的解法。
一元二次不等式ax2+bx+c>0(或<0)的解可以联系二次函数y=ax2+bx+c的图象(a≠0)图象在x轴上方部分对应的x值为不等式ax2+bx+c>0的解,图象在x轴下方部分对应的x值为不等式ax2+bx+c<0的解。
而方程ax2+bx+c=0的根表示图象与x轴交点的横坐标。
求解一元二次不等式的步骤,先把二次项系数化为正数,再解对应的一元二次方程,最后根据一元二次方程的根,结合不等号的方向,写出不等式的解集。
x2+3x-4<0 (x+4)(x-1)<0 或或-4<x<1或。
原不等式解集为{x|-4<x<1}。
x2+3x-4<0 (x+)2<|x+|<-<x+<-4<x<1原不等式解集为{x|-4<x<1}。
例1.解关于x的不等式|ax-2|<4,其中a∈R。
解:|ax-2|<4属于|x|<c(c>0)型。
∴-4<ax-2<4, 不等号各端加2,得-2<ax<6。
当a>0时,-<x<,当a<0时,->x>, 当a=0时不等式化为2<4,显然x∈故a>0时不等式解集是{x|-<x<},a<0时不等式解集是{x|<x<-},a=0时不等式解集是R。




