初二数学-特殊四边形中的动点问题(教师版)

四边形动点问题解题技巧引言四边形动点问题是数学中常见的一个问题，也称为四边形运动几何问题。

它涉及到一个四边形，其中三个顶点是固定不动的，而第四个顶点在运动当中。

本文将介绍四边形动点问题的基本概念和解题技巧，以帮助读者更好地理解和解决这类问题。

基本概念在开始讨论四边形动点问题之前，我们先来了解一些基本概念：1.四边形：四边形是由四个线段连接在一起形成的几何图形。

它有四个顶点和四条边。

2.动点：动点是指在一定时间内位置发生改变的点。

在四边形动点问题中，通常涉及到一个顶点作为动点，其位置会随着时间的变化而变化。

解题技巧解决四边形动点问题的关键是要能够分析和利用几何图形的性质。

以下是一些常用的解题技巧：折线法折线法是解决四边形动点问题的常用方法之一。

具体步骤如下：1.根据题目所给条件，确定四边形的固定顶点和动点。

2.假设动点在某一时刻位于四边形的某个位置，通过分析几何性质，确定其他顶点和边的位置。

3.根据动点随时间的变化，得出四边形其他顶点和边的变化规律。

4.利用求解几何图形的方法，求出动点的运动轨迹。

5.根据题目要求，确定动点的最终位置或特性。

共线关系在解决四边形动点问题时，有时可以利用共线关系来简化求解过程。

当四边形的三个固定顶点及其对应的边共线时，可以利用相似三角形的性质来求解动点的位置。

各种特殊情况的考虑在解决四边形动点问题时，有时需要考虑一些特殊情况，如四边形退化为三角形的情况、四边形退化为直线的情况等。

针对不同的特殊情况，需要采取相应的分析方法和解题技巧。

解题示例下面通过一个具体的例子来演示如何应用解题技巧解决四边形动点问题。

例题：一个矩形的两个对角线交于点O，其中一个顶点A固定不动，另一个顶点B在矩形的一侧边上以一定速度向下移动。

求矩形的另外两个顶点C和D的运动轨迹。

解答： 1. 设矩形的高为h，宽为w，动点B的初始位置为(0, h)。

2.假设动点B的坐标为(x, y)，根据矩形的性质，可以确定顶点C和D的坐标：–顶点C的坐标为(x+w, y)；–顶点D的坐标为(x+w, y-h)。

四边形之存在性问题（一）（讲义）一、知识点睛存在性问题处理框架： 1. 理解题意，整合信息． 2. 根据不变特征，确定分类标准．不变特征举例：（1）平行四边形存在性问题以定线段作边或对角线，确定分类．常借助对应边相等、坐标间关系及中点坐标公式建等式求解．（2）特殊平行四边形存在性问题①菱形存在性问题，转化为等腰三角形存在性问题； ②正方形存在性问题，转化为等腰直角三角形存在性问题． 3. 分析特殊状态的形成因素，画出符合题意的图形并求解． 4. 结果验证．二、精讲精练1.在坐标平面上的点D 处，则在坐标平面内是否存在点P，使得以A ，O ，D ，P 为顶点的四边形是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．2. 如图，在平面直角坐标系xOy 中，直线334y x =-+与x 轴、y 轴分别交于点A ，B ，点C 的坐标为(0，2-)．若点D 在直线AB 上运动，点E 在直线AC上运动，当以O ，A ，D ，E 为顶点的四边形是平行四边形时，求点D 的坐标．3. 如图，在平面直角坐标系xOy 中，四边形OABC 是直角梯形，BC ∥OA ，∠112y x =-+经过点A ，且与y 轴交于点D ．若M 是直线AD 上的一个动点，则在x 轴上是否存在点N ，使得以O ，B ，M ，N 为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．4. 如图，在平面直角坐标系xOy 中，四边形OABC 是矩形，顶点A ，C 分别在x 轴、y 轴上，顶点B 的坐标为(3，4)，点E 在OC 边上，点F 的坐标为(2，4)．将矩形OABC 沿直线EF 折叠，点C 落在AB 边上的点G 处，若点N 在x 轴上，则直线EF 上是否存在点M ，使得以M ，N ，F ，G 为顶点的四边形是平行四边形？若存在，求出点M 的坐标；若不存在，请说明理由．5. 如图，在平面直角坐标系xOy 中，直线1y x =+与24y x =-+交于点A ，两直线与x 轴分别交于点B 和点C ，D 是直线AC 上的一个动点．直线AB 上是否存在点E ，使得以E ，D ，O ，A 为顶点的四边形是平行四边形？若存在，求出点E 的坐标；若不存在，请说明理由．三、回顾与思考【参考答案】1．存在，点P的坐标为(-3)，(3)或(3-)．2．点D的坐标为(125，65)或(285，65-)．3．存在，点N的坐标为(3-，0)，(7，0)或(3，0)．4．存在，点M的坐标为(93-，(33-，或(33+，8)．5．存在，点E的坐标为(13-，23)或(73，103)．四边形之存在性问题（一）（随堂测试）1.如图，已知在平面直角坐标系xOy中，直线y=+与x轴、y轴分别交于点A，B，直线BC与x轴交于点C，且∠ABC=60°．若D为直线AB上一点，E为直线BC上一点，且以O，B，D，E为顶点的四边形是平行四边形，求点D的坐标．【参考答案】1．点D 的坐标为(2，2，四边形之存在性问题（一）（作业）2. 如图，在平面直角坐标系xOy中，直线23y x =+与x 轴、y 轴分别交于点A ，B ，点C 在y 轴正半轴上，且1OB =，直线CD ⊥AB 于点P ，交x 轴于点D3. 如图，在平面直角坐标系xOy 中，矩形OABC 的顶点A ，C 分别在x 轴、y 轴的正半轴上，点D 在OA 边上，点E 在OC 边上，将矩形OABC 沿直线DE 折43=．已知OC =8，BC =12，OD =10，请解答下列问题． （1）求直线DE 的解析式．（2）若M 为直线DF 上一点，则在直线DE 上是否存在点N ，使得以A ，D ，M ，N 为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．【参考答案】3)．四边形之存在性问题（二）（讲义）1.如图，在平面直角坐标系xOy中，□ABCD的顶点A，B的坐标分别为A(0，3)，B(，0)，顶点C在x轴正半轴上，顶点D在第一象限，且2.如图，在平面直角坐标系xOy中，直角梯形OABC的顶点A在y轴正半轴上，顶点C的坐标为(18-，0)，A B∥O C，∠OCB=45°，且BC=（1）求点B的坐标．（2）直线BE与线段OA交于点E，且OE=6．若P是直线BE上的一动点，则在坐标平面内是否存在点Q，使得以O，E，P，Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．3.如图，在平面直角坐标系中，已知点A，B，C的坐标分别为A(9-，0)，B(16，0)，C(0，12)，D是线段BC上的一动点（不与点B，C重合），过点D作直线DE⊥OB，垂足为点E．若M为坐标平面内一点，则在直线DE上是否存在点N，使得以C，B，M，N为顶点的四边形是正方形？若存在，求出点N的坐标；若不存在，请说明理由．4.如图，在平面直角坐标系xOy中，矩形OABC的顶点A，C分别在x轴、y轴的正半轴上，顶点B的坐标为(8，6)．若点D在第一象限内的直线l：=-上，点P在AB边上，AP=m，Q为坐标平面内一点，且以C，P，y x26D，Q为顶点的四边形是正方形，求m的值．三、回顾与思考【参考答案】1．存在，12(F F 2．（1）B (-6，12)；（2）存在，1234(66)((33)Q Q Q Q ---，或或或，3．存在，1234(1228)(416)(1414)(22)N N N N --，或，或，或， 4．存在，142633m m m ===，或四边形之存在性问题（二）（随堂测试）1. 如图，在平面直角坐标系中，直线l 1分别与x 轴、y 轴交于点A ，B ，直线l 2与直线l 1交于点C ，已知B (0，6)，C (4，2)，若P 为坐标平面内一点，则在直线l 1上是否存在一点Q ，使以O ，B ，P ，Q 为顶点的四边形是菱形？若存在，求出点Q 的坐标；若不存在，请说明理由.【参考答案】1．存在，1234(60)((33)Q Q Q Q --+，或或或，四边形之存在性问题（二）（作业）1. 如图，平面直角坐标系中，矩形OABC 的对角线AC =12，AO =6，把矩形沿直线DE 对折使点C 落在点A 处，DE 与AC 相交于点F ，若M 为坐标平面内一点，则在直线DE 上是否存在点N ，使以O ，F ，M ，N 为顶点的四边形是菱形？若存在，求出点N 的坐标；若不存在，请说明理由．2. 如图，在平面直角坐标系中，直线y 1=2x 与直线y 2=-6x +48交于点A ，另有一直线平行于x 轴，分别交线段OA ，AB 于M ，N 两点，点R 在x 轴上，在坐标平面内，是否存在这样的点Q ，使得以R ，M ，N ，Q 为顶点的四边形是正1．存在，123433(06)(3N N N N ---++，或，或 2．存在，12336129(0)(0)(6)552Q Q Q ，或，或，四边形之动点问题（讲义）一、知识点睛1.动点问题处理框架．①研究基本图形；②分析运动过程，分段，定范围；③分析几何特征、表达、设计方案求解．2.分析运动过程常借助运动状态分析图，需关注四要素．①起点、终点——确定时间范围；②速度（注意速度是否变化）；③状态转折点——确定分段，常见状态转折点有拐点、碰撞点等；④所求目标——明确方向．二、精讲精练1.如图，在Rt△ABC中，∠B=90°，BC=C=30°．点D从点C出发，沿CA方向以每秒2个单位长度的速度向点A匀速运动，点E从点A同时出发，沿AB方向以每秒1个单位长度的速度向点B匀速运动，当其中一点到达终点时，另一点也随之停止运动．设点D，E运动的时间为t秒（0t ），过点D作DF⊥BC于点F，连接DE，EF．（1）求证：AE=DF．（2）四边形AEFD能成为菱形吗？若能，求出相应的t值；若不能，请说明理由．（3）当t为何值时，△DEF为直角三角形？请说明理由．EACB2.如图，在梯形ABCD中，∠B=90°，AD∥BC，E是BC边的中点，且AB=AD=BE=2cm．动点P从点B出发，以1cm/s的速度沿B→A→D→E的方向匀速运动，动点Q从点B同时出发，以相同的速度沿B→E→C→E的方向匀速运动．过点P作PF⊥BC于点F，设△PFQ的面积为S，点P运动的时间为t（s）（06t<<）．（1）当点P在AB上运动时，直接判断△PFQ的形状．（2）在运动过程中，四边形PQCD能成为哪些特殊的四边形？请写出相应的t的取值范围．（直接回答，无需证明）（3）求S与t之间的函数关系式．3.已知，在矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线分别交AD，BC于点E，F，垂足为点O．（1）如图1，连接AF，CE，求证四边形AFCE是菱形，并求出AF的长．（2）如图2，动点P，Q分别从A，C两点同时出发，沿△AFB和△CDE的各边匀速运动一周．即点P沿A→F→B→A的方向运动，点Q沿C→D→E→C的方向运动．①若点P的速度为5cm/s，点Q的速度为4cm/s，运动时间为t s，当以A，C，P，Q为顶点的四边形是平行四边形时，求t的值．②若点P，Q运动的路程分别为a，b（单位：cm，0ab≠），当以A，C，P，Q为顶点的四边形是平行四边形时，求a与b之间的数量关系．O F E DCBAQ4.如图，在菱形ABCD中，AB=10，∠ABC=60°．点Q从点D出发，沿折线DC-CA-AB以每秒3个单位长度的速度匀速运动；点P从点B同时出发，沿BC以每秒1个单位长度的速度匀速运动，当点Q到达点B时，P，Q两点同时停止运动．过点P作射线PK⊥BC，交折线BA-AC于点E，交直线AD于点F，设运动的时间为t秒．（1）当t为何值时，BP=AF？（2）当t为何值时，QE⊥AB？（3）设直线PK扫过菱形ABCD的面积为S，试求S与t之间的函数关系式．D三、回顾与思考【参考答案】1.（1）（略）；（2）103t =；（3）542t t ==或2.（1）△PFQ 是等腰直角三角形（2）当0<t <2时，四边形PQCD 是梯形；当2≤t ≤4时，四边形PQCD 是平行四边形；当4<t <6时，四边形PQCD 是等腰梯形（3）221(02)22(24)1618(46)2tt S t t t t ⎧<⎪⎪=<⎨⎪⎪-+<<⎩≤≤3.（1）AF =5；（2）①43t =；②a +b =12 4.（1）52t =；（2）1532t t ==或；（3）2(05)(510)t S t =⎨⎪<⎪⎩≤≤≤四边形之动点问题（随堂测试）1． 如图，在直角梯形ABCD 中，AD ∥BC ，∠A =90°，BC =21，AD =16．动点P 从点B出发，沿线段BC 的方向以每秒2个单位长的速度向点C 运动，同时动点Q 从点A 出发，在线段AD 上以每秒1个单位长的速度向点D 运动，当其中一个动点到达终点时，另一个动点也随之停止运动．设运动的时间为t 秒． （1）当t 为何值时，以点P ，C ，D ，Q 为顶点的四边形是平行 四边形？（2）当t 为何值时，PD =PQ ？DCBAP QAB CD【参考答案】1. （1）5t =；（2）163t =四边形之动点问题（作业）1. 如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC =90°，AD =4，DC =6，BC =7，梯形的高为M 从B 点出发沿BC 以每秒1个单位长的速度向终点C 运动，动点N 从C 点出发沿C —D —A 以每秒2个单位长的速度向终点A 运动．若M ，N 两点同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t 秒（t >0）． （1）用t 表示△CMN 的面积S ；（2）当t 为何值时，四边形ABMN 为矩形？ （3）当t 为何值时，四边形CDNM 为平行四边形？BCDA2. 如图，在直角梯形ABCD 中，∠B =90°，AD ∥BC ，且AD =4 cm ，BC =9 cm ，DC =10 cm ．若动点P 从A 点出发，以每秒2 cm 的速度沿线段AD ，DC 向C 点运动；动点Q 从C 点出发以每秒1 cm 的速度沿CB 向B 点运动．当P 点到达C 点时，动点Q 同时停止运动．设点P ，Q 同时出发，运动时间为t 秒．（1）当t 为何值时，四边形PQCD是平行四边形？ （2）当t 为何值时，PQ ⊥DC ？3. 如图所示，在直角梯形ABCD 中，AD ∥BC ，∠A =90°， BC =21，AD =10．动点P 从点C 出发，沿线段CB 的方向以每秒2个单位长的速度向点B 运动，动点Q 同时从点A 出发，在线段AD 上以每秒1个单位长的速度向点D 运动，当其中一个动点到达终点时，另一个动点也随之停止运动．设运动的时间为t 秒．（1）当t 为何值时，四边形PCDQ 是平行四边形？ （2）当t 为何值时，PD =PQ ？DCB A【参考答案】1. （1）2(03)5)t S t ⎧+<⎪⎪=⎨⎪<⎪⎩≤≤ （2）103t =（3）133t =2.（1）43t =；（2）285t =3.（1）103t =；（2）325t =或t =10四边形综合训练（每日一题）1.（5月19日）如图，在平面直角坐标系中，直线1y x=+交于点=-+与3y xA，与x轴分别交于点B和点C，D是直线AC上一动点，则直线AB上是否存在一动点E，使得以O，D，A，E为顶点的四边形是平行四边形？若存在，请求出点E的坐标；若不存在，请说明理由．2.（5月20日）如图，在平面直角坐标系中，函数y=2x+12的图象分别交x轴、y轴于A，B两点．过点A的直线交y轴正半轴于点M，且点M为线段OB的中点．C是直线AB上一动点，则在直线AM上是否存在一点D，使以A，O，C，D为顶点的四边形是平行四边形？若存在，求出点C的坐标；若P从点A出发，沿AB以每秒2 cm的速度向点B运动，点Q从点C出发，沿CA以每秒1 cm的速度向点A运动．设点P，Q同时出发，运动时间为t秒（0<t<6）．（1）直接写出线段AP，AQ的长（用含t的代数式表示）：AP=_________，AQ=________；（2）连接PC，并把△PQC沿QC翻折，得到四边形PQP'C，那么是否存在某一时刻t，使四边形PQP'C为菱形？若存在，求出t的值；若不存在，说明理由．3. （5月22日）如图，在等腰梯形ABCD 中，AD ∥BC ，DE ⊥BC 于E ，且DE=AD =18，∠C =60°． （1）BC =_____；（2）若动点P 从点D 出发，速度为2个单位/秒，沿DA 向点A 运动，同时，动点Q 从点B 出发，速度为3个单位/秒，沿BC 向点C 运动，当一个动点到达终点时，另一个动点也随之停止运动，设运动的时间为t 秒． ①当t =_____秒时，四边形PQED 是矩形；②当t 为何值时，线段PQ 与梯形ABCD 的边构成平行四 边形？③是否存在t 值，使②中的平行四边形是菱形？若存在，请求出t 值；若不存在，请说明理由．Q PEDCBAAB CDE4. （5月23日）如图，在梯形ABCD 中，AD ∥BC ，AD =6，BC =16，E 是BC的中点．点P 以每秒1个单位长度的速度从点A 出发，沿AD 向点D 运动，同时点Q 以每秒2个单位长度的速度从点C 出发，沿CB 向点B 运动．点P 停止运动时，点Q 也随之停止运动．当t 为何值时，以点P ，Q ，E ，D 为顶点的四边形是平行四边形？【参考答案】1.121157()()2222E E -，或，2.12(012)(1212)C C --，或， 3.（1）AP =2t ，AQ =6-t ；（2）t =44.（1）26；（2）①225t =；②182655t t ==或；③不存在5.1423t t ==或。

四边形中的动点问题(带答案)四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是_____________2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H分别为边AD，AB，BC，CD 的中点．若AC＝8，BD＝6，则四边形EFGH 的面积为________3、如图，正方形ABCD的边长为4，点P在DC 边上，且DP＝1，点Q是AC上一动点，则DQ＋PQ 的最小值为____________4、如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E 运动的时间是t s(0 < t ≤15)．过点D作DF ⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t. （1）连接EF，当EF经过AC边的中点D时，（1）求证：△ADE≌△CDF；：（2）当t为______s时，四边形ACFE是菱形；6、在菱形ABCD中，∠B=60°，点E在射线BC 上运动，∠EAF=60°，点F在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点E在BC的延长线上时（如图2），线段EC、CF、AB有怎样的相等关系？写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN是平行四边形；（2）填空：①当AM的值为______时，四边形AMDN是矩形；②当AM的值为______时，四边形AMDN是菱形．8、如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D重合）分别向直线AB、AD作垂线，垂足分别为E、F．（1）BD的长是______；（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______10、如图，∠MON=90°，矩形ABCD的顶点A、B 分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为______．11、如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN 是菱形；（3）四边形PMEN有可能是矩形吗？若有可能，求出AP的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A 运动，其速度为0.5cm／s。

====Word 行业资料分享--可编辑版本--双击可删====人教版八年级特殊四边形中的动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 数形结合思想 转化思想1、如图，在四边形ABCD 中，E F G H 、、、分别是AB BC CD DA 、、、边上的中点，阅读下列材料，回答问题：⑴连结AC BD 、，由三角形中位线的性质定理可证四边形EFGH 是 . ⑵对角线AC BD 、满足条件 时，四边形EFGH 是矩形. ⑶对角线AC BD 、满足条件 时，四边形EFGH 是菱形. ⑷对角线AC BD 、满足条件 时，四边形EFGH 是正方形.N OHGFEABCD2、如图1，梯形ABCD 中，AD ∥BC ，90B ︒∠=，14,18,21AB cm AD cm BC cm ===，点P 从A 开始沿AD 边以1cm/秒的速度移动，点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动，如果,P Q 分别从,A C 同时出发，设移动时间为t t = 时，四边形是平行四边形；当t = 时，四边形是等腰梯形.3、如图2，正方形ABCD 的边长为4，点M 在边DC 上，且1DM =，N 为对角线AC 上任意一点，则DN MN +的最小值为4、在△ABC 中，90ACB ︒∠=，AC BC =，直线MN 经过点C ，且AD MN ⊥于D ，BE MN ⊥于E .CB A E D图1N M AB CD E M N 图2 A CB ED N M 图3(1)当直线MN 绕点C 旋转到图1的位置时，求证：DE AD BE =+； (2)当直线MN 绕点C 旋转到图2的位置时，求证：DE AD BE =-；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE AD BE 、、具有怎样的等量关系？请写出这个等量关系，并加以证明.5、如图，在梯形ABCD中，3545AD BC AD DC AB B ====︒∥，，，．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒． （1）求BC 的长．（2）当MN AB ∥时，求t 的值．（3）试探究：t 为何值时，MNC △为等腰三角形．6、在矩形ABCD 中，204AB cm BC cm ==，，点P 从A 开始沿折线A B C D →→→以4/cm s 的速度运动，点Q 从C 开始沿CD 边以1/cm s 的速度移动，如果点P Q 、分别从A C 、同时出发，当其中一点到达点D 时，另一点也随之停止运动，设运动时间为()t s ，t 为何值时，四边形APQD 也为矩形？C7、如图，梯形OABC 中, O 为直角坐标系的原点, A B C 、、的坐标分别为（14，0）、（14，3）、（4，3）点P Q 、同时从原点出发，分别作匀速运动，点P 沿OA 以每秒1个单位向终点A 运动，点Q 沿OC CB 、以每秒2个单位向终点B 运动。

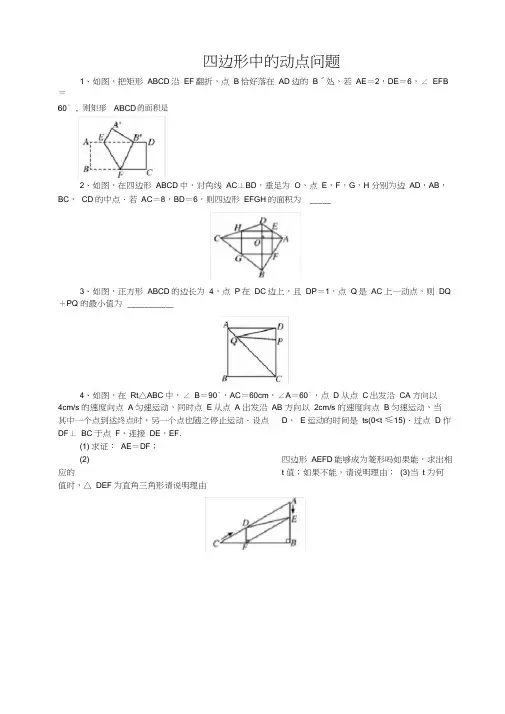
四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠ EFB ＝2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H 分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH的面积为 _____3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ ＋PQ 的最小值为___________4、如图，在Rt△ABC中，∠ B＝90°，AC＝60cm，∠A＝60°，点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动，同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts(0<t ≤15)．过点 D 作DF⊥ BC于点F，连接DE，EF.(1) 求证：AE＝DF；(2) 四边形AEFD能够成为菱形吗如果能，求出相应的t 值；如果不能，请说明理由；(3)当t 为何值时，△ DEF为直角三角形请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点 A 出发沿射线AG以1cm/s 的速度运动，同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动，设运动时间为t.（1）连接EF，当EF经过AC边的中点 D 时，（1）求证：△ ADE≌△ CDF；：（2）当t 为____ s 时，四边形ACFE是菱形；6、在菱形ABCD中，∠ B=60°，点E在射线BC上运动，∠ EAF=60°，点 F 在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点 E 在BC的延长线上时（如图2），线段EC、CF、AB 有怎样的相等关系写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠ DAB=60°，点E是AD边的中点．点M 是AB边上一动点不与点 A 重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN 是平行四边形；（2）填空：①当AM 的值为____ 时，四边形AMDN 是矩形；②当AM 的值为____ 时，四边形AMDN 是菱形．8、如图，△ ABC中，点O 是边AC上一个动点，过O 作直线MN ∥BC，设MN 交∠ BCA的平分线于点E，交∠ BCA 的外角平分线于点F．（1）探究：线段OE与OF 的数量关系并加以证明；（2）当点O 运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形（3）当点O 在边AC上运动时，四边形BCFE会是菱形吗若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD 作垂线，垂足分别为E、F．（1）BD的长是___ ；（2）连接PC，当PE+PF+PC取得最小值时，此时PB 的长是__10、如图，∠ MON=90°，矩形ABCD的顶点A、B分别在边OM，ON 上，当B在边ON 上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O 的最大距离为_____ ．11、如图，已知矩形ABCD，AD=4，CD=10，P 是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN 是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN 是菱形；（3）四边形PMEN有可能是矩形吗若有可能，求出AP 的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A 运动，其速度为／s。

专题5特殊平行四边形的动点问题类型一、一般动点问题【例1】如图，在Rt ABC ∆中，90,60B AC ∠=︒=cm,60A ∠=︒，点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以2cm/s 的速度向点B 匀速运动.当其中一个点到达终点时，另一个点也随之停止运动.设点,D E 运动的时间是t s (015)t <≤.过点D 作DF BC ⊥于点F ，连接,DE EF .（1）求证：AE=DF ；（2）四边形AEFD 能够成为菱形吗？如果能，求出相应的t 值，如果不能，说明理由；（3）当t 为何值时，△DEF 为直角三角形？请说明理由.【解答】（1）证明：根据题意可知CD=4t ，AE=2t ，∵∠B=90°，∠A=60°，∴∠C=30°，∴DF=21DC=2t.∵AE=2t ，DF=2t ，∴AE=DF.（2）能.理由如下：∵AB ⊥BC ，DF ⊥BC ，∴AE ∥DF.∵AE=DF ，AE ∥DF ，∴四边形AEFD 为平行四边形，∴要使平行四边形AEFD 为菱形，则需AE=AD ，即2t=60-4t ，解得t=10，∴当t=10时，四边形AEFD 为菱形.（3）根据题意可知需分∠EDF=90°或∠DEF=90°两种情况讨论.①当∠EDF=90°时，∵∠EDF=∠B=∠DFE=90°，∴四边形DEBF 是矩形，∴∠DEB=90°，∴∠AED=90°.∵∠AED=90°，∠A=60°，∴∠ADE=30°.∵∠AED=90°，∠ADE=30°，∴AD=2AE ，即60-4t=4t ，解得t=215.②当∠DEF=90°时，∵四边形AEFD 为平行四边形，∴EF ∥AD ，∴∠ADE=∠DEF=90°.∵∠ADE=90°，∠A=60°，∴AD=21AE ，即60-4t=21×2t ，解得t=12.综上所述，当t=215或12时，△DEF 为直角三角形.【例2】如图在平面直角坐标系中，A (16，0)、C (0，8)，四边形OABC 是矩形，D 、E 分别是OA 、BC 边上的点，沿DE 折叠矩形，点A 恰好落往y 轴上的点C 处，点B 落B '处。

八年级下册数学《第十八章 平行四边形》 专题 利用特殊四边形的性质巧解动点问题【例题1】（2021春•费县期中）如图所示，在四边形ABCD 中，AD ∥BC ，AD ＝27cm ，BC ＝36cm ，点P 从A 向点D 以1cm /s 的速度运动，到点D 即停止．点Q 从点C 向点B 以2cm /s 的速度运动，到点B 即停止．直线PQ 将四边形ABCD 截成两个四边形，分别为四边形ABQP 和四边形PQCD ，则当P ，Q 两点同时出发，几秒后所截得两个四边形中，其中一个四边形为平行四边形？【变式11】（2021春•阳谷县期末）如图，在四边形ABCD中，AD∥BC，且AD＜BC，BC=6cm,动点P，Q分别从点D，B同时出发，点P以1cm/s的速度向点A方向运动，点Q以2cm/s的速度向点C运动，几秒后四边形CDPQ是平行四边形（）A．1 B．2 C．3 D．4【变式12】（2021秋•抚州期末）如图，在▱ABCD中，对角线BD⊥AD，AB＝16，∠A＝60°，O为BD 的中点，E为边AB上一动点，以2cm/s的速度从A点向B点运动，运动时间为ts，连接EO并延长交CD 于点F，连接DE、BF，下列结论不成立的是（）A．四边形DEBF为平行四边形B．若t＝4，则四边形DEBF为菱形C．若t＝2，则四边形DEBF为矩形D．若t＝6，则四边形DEBF为正方形【变式13】如图，在四边形ABCD中，AD∥BC且AD＝9cm，BC＝6cm，点P、Q分别从点A、C同时出发，点P以1cm/s的速度由A向D运动，点Q以2cm/s的速度由C向B运动．问几秒后直线PQ将四边形ABCD截出一个平行四边形？【变式14】（2021春•闽侯县月考）如图，四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，点P 自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，则当P，Q同时出发，设运动时间为t（s）．（1）当t为何值时，四边形APQB为平行四边形？（2）当t为何值时，四边形PDCQ为平行四边形？【变式15】（2022春•滨湖区期末）如图，∠ABC＝45°，AB＝2，BC＝2√2，点P为BC上一动点，AQ ∥BC，CQ∥AP，AQ、CQ交于点Q，则四边形APCQ的形状是，连接PQ，当PQ取得最小值时，四边形APCQ的周长为．【变式16】如图，在△ABC中，∠BAC＝90°，∠B＝45°，BC＝10，过点A作AD∥BC，且点D在点A的右侧．点P从点A出发沿射线AD方向以每秒1个单位的速度运动，同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动，在线段QC上取点E，使得QE＝2，连接PE，设点P的运动时间为t秒．（1）若PE⊥BC，求BQ的长；（2）请问是否存在t的值，使以A，B，E，P为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由．【变式17】如图，等边△ABC的边长为10cm，动点M从点B出发，沿B→A→C→B的方向以4cm/s的速度运动，动点N从点C出发，沿C→A→B→C方向以3cm/s的速度运动．（1）若动点M、N同时出发，经过几秒钟两点第一次相遇？（2）若动点M、N同时出发，且其中一点到达终点时，另一点即停止运动．那么运动到第几秒钟时，点A、M、N以及△ABC的边上一点D恰能构成一个平行四边形？求出时间t并请指出此时点D的具体位置．【变式18】（2021春•惠来县期末）如图，在△ABC中，AB＝AC＝20cm，BD⊥AC于点D，且BD＝16cm．点M从点A出发，沿AC方向匀速运动，速度为4cm/s；同时点P由B点出发，沿BA方向匀速运动，速度为1cm/s，过点P的直线PQ∥AC，交BC于点Q，连接PM，设运动时间为t（s）（0＜t＜5），解答下列问题：（1）线段AD＝cm；（2）求证：PB＝PQ；（3）当t为何值时，以P、Q、D、M为顶点的四边形是平行四边形？【例题2】（2021秋•迁安市期末）如图，在长方形ABCD 中，AB ＝CD ＝8cm ，BC ＝12cm ，点P 从点B出发，以2cm /秒的速度沿BC 向点C 运动，同时，点Q 由点C 出发，以相同的速度沿CD 向点D 运动，设点P 的运动时间为t 秒，当△ABP ≌△PCQ 时，t 的值为（ ）A ．1或3B ．2C ．2或4D ．1或2【变式21】（2022春•玄武区校级期中）如图，在矩形ABCD 中，AB ＝4，BC ＝8，点E 在BC 边上，且BE ＝3，F 为AB 边上的一个动点，连接EF ，以EF 为边作正方形EFGH ，且点H 在矩形ABCD 内，连接CH ，则CH 的最小值为（ ）A ．3B ．4C ．√8D ．√10【变式22】（2022春•新洲区期中）如图，矩形ABCD 中，AB ＝8，AD ＝2，点E 从D 向C 以每秒1个单位的速度运动，以AE 为一边在AE 的左上方作正方形AEFG ，同时垂直于CD 的直线MN 也从C 向D 以每秒2个单位的速度运动，当点F 落在直线MN 上，设运动的时间为t ，则t 的值为（ ）A ．1B ．4C ．103D ．143【变式23】如图，矩形ACBE中，AC＝12，BC＝5，点M在边AB上，且AM＝6，动点D在矩形边上运动一周，能使△ADM是以∠AMD为顶角的等腰三角形共有（）A．3个B．4个C．5个D．6个【变式24】如图，在矩形ABCD中，AB＝3，AD＝4，点P，Q分别是边BC和CD上的两个动点（可以与线段的端点重合，但P，Q两点不重合），点E、F分别是P A和PQ的中点，在两个动点的移动过程中，线段EF的长度取值范围是．【变式25】如图，在长方形ABCD中，AB＝5cm，AD＝3cm．点E从点A出发，以每秒2cm的速度沿折线ABC方向运动，点F从点C出发，以每秒1cm的速度沿线段CD方向向点D运动．已知动点E、F 同时发，当点E运动到点C时，E、F停止运动，设运动时间为t．（1）当E运动到B点时，求出t的值；（2）在点E、点F的运动过程中，是否存在某一时刻，使得EF＝3cm？若存在，请求出t的值；若不存在，请说明理由．【变式26】如图，在长方形ABCD中，AB＝8cm，BC＝12cm，点P从点B出发，以2cm/秒的速度沿BC 向点C运动，设点P的运动时间为t秒．（1）如图1，S△DCP＝．（用t的代数式表示）（2）如图1，当t＝3时，试说明：△ABP≌△DCP．（3）如图2，当点P从点B开始运动的同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．【变式27】（2022春•黄州区校级期中）如图，在矩形ABCD中，AB＝3cm，BC＝4cm，E，F是对角线AC上的两个动点，分别从A，C同时出发相向而行，速度均为1cm/s，运动时间为ts（0≤t≤5）．（1）AE＝t，EF＝．（2）若G，H分别是AB，DC的中点，求证：四边形EGFH是平行四边形．（3）在（2）的条件下，当t为何值时，四边形EGFH为矩形？【变式28】（2021•合川区校级模拟）如图，在四边形ABCD中，∠A＝∠B＝∠BCD＝90°，AB＝DC ＝4，AD＝BC＝8．延长BC到E，使CE＝3，连接DE，由直角三角形的性质可知DE＝5．动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒．（t＞0）（1）当t＝3时，BP＝；（2）当t＝时，点P运动到∠B的角平分线上；（3）请用含t的代数式表示△ABP的面积S；（4）当0＜t＜6时，直接写出点P到四边形ABED相邻两边距离相等时t的值．【例题3】如图，在菱形ABCD中，∠A＝60°，E，F分别为AD，DC上的动点，∠EBF＝60°，点E 从点A向点D运动的过程中，AE+CF的长度（）A．逐渐增加B．保持不变且与EF的长度相等C．逐渐减小D．保持不变且与AB的长度相等【变式31】（2022春•西湖区期末）如图，在菱形ABCD 中，∠B ＝60°，点P 从点B 出发，沿折线B一C 一D 方向移动，移动到点D 停止，连结AP ，DP ．在△DAP 形状的变化过程中，出现的特殊三角形有：①等腰三角形；②等边三角形；③直角三角形，以下排序正确的是（ ）A ．①③②③B ．③②①③C ．①③②①D ．③②③①【变式32】（2022•槐荫区一模）如图，菱形ABCD 中对角线AC 与BD 相交于点F ，且AC ＝8，BD =8√3，若点P 是对角线BD 上一动点，连接AP ，将AP 绕点A 逆时针旋转使得∠P AE ＝∠BAD ，连接PE ，取AD 的中点O ，连接OE ，则在点P 的运动过程中，线段OE 的最小值为（ ）A ．2B ．4C ．4√3D ．4√2【变式33】（2021春•仙桃期末）如图，在菱形ABCD 中，AB ＝5cm ，∠ADC ＝120°，点E 、F 同时由A 、C 两点出发，分别沿AB 、CB 方向向点B 匀速移动（到点B 为止），点E 的速度为1cm /s ，点F 的速度为2cm /s ，经过t 秒△DEF 为等边三角形，则t 的值为（ ）A ．34B ．43C ．32D ．53【变式34】如图，在菱形ABCD中，对角线AC、BD相交于点O．AC＝8cm，BD＝6cm，点P为AC上一动点，点P以1cm/s的速度从点A出发沿AC向点C运动．设运动时间为ts，当t＝s时，△P AB为等腰三角形．【变式35】（2021•江西模拟）如图，在菱形ABCD中，AB＝6√3，∠ABC＝60°，AE⊥BC于点E，交BD于点F．若P是菱形ABCD边上的一动点，当△AFP的面积是9√3时，DP的长为．【变式36】如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．（1）求证：四边形PBQD是平行四边形；（2）若AD＝8cm，AB＝6cm，P从点A出发，以1cm/秒的速度向D运动（不与D重合），设点P运动时间为t秒．①请用t表示PD的长；②求t为何值时，四边形PBQD是菱形．【变式37】（2022春•桥西区校级期中）如图所示，在菱形ABCD 中，AB ＝8，∠BAD ＝120°，△AEF 为等边三角形，点E 、F 分别在菱形的边BC 、CD 上滑动，且E 、F 不与B 、C 、D 重合．（1）证明不论E 、F 在BC 、CD 上如何滑动，总有BE ＝CF ．（2）当点E 、F 在BC 、CD 上滑动时，分别探讨四边形AECF 和△CEF 的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．【变式38】如图，在菱形ABCD 中，AB ＝2cm ，∠ADC ＝120°．动点E 、F 分别从点B 、D 同时出发，都以0.5cm /s 的速度向点A 、C 运动，连接AF 、CE ，分别取AF 、CE 的中点G 、H ．设运动的时间为ts （0＜t ＜4）．（1）求证：AF ∥CE ；（2）当t 为何值时，△ADF 的面积为√32cm 2； （3）连接GE 、FH ．当t 为何值时，四边形EHFG 为菱形．【例题4】如图，点P 是正方形ABCD 的BC 边上一动点，PE ⊥BD 于E ，PF ⊥AC 于F ，若AC ＝12，则PE +PF 的值是（ ）A ．6B ．10C ．6√2 D ．12【变式41】正方形ABCD 的边AB 上有一动点E ，以EC 为边作矩形ECFG ，且边FG 过点D ．在点E 从点A 移动到点B 的过程中，矩形ECFG 的面积（ ）A ．先变大后变小B ．先变小后变大C ．一直变大D ．保持不变 【变式42】（2022•乐陵市模拟）如图，在正方形ABCD 中，已知边长AB ＝5，点E 是BC 边上一动点（点E 不与B 、C 重合），连接AE ，作点B 关于直线AE 的对称点F ，则线段CF 的最小值为（ ）A ．54B ．5√2−5C ．5√22D ．52【变式43】（2021春•金寨县期末）如图，在边长为2的正方形ABCD中，点M为对角线BD上一动点，ME⊥BC于点E，MF⊥CD于点F，连接EF，则EF的最小值为（）A．1B．2√2C．√3D．√2【变式44】（2021•东阿县三模）如图，正方形ABCD的边长为2，E为AB边的中点，点F在BC边上，点B关于直线EF的对称点记为B'，连接B'D，B'E，B'F．当点F在BC边上移动使得四边形BEB'F成为正方形时，B'D的长为（）A．√2B．√3C．2√2D．3【变式45】如图，在边长为8的正方形ABCD中，E、F分别是边AB、BC上的动点，且EF＝6，M为EF中点，P是边AD上的一个动点，则CP+PM的最小值是（）A．10B．8√5−3C．6√5+3D．3√3+5【变式46】（2021春•潼南区期末）如图，在正方形ABCD中，E、F分别为BC、CD上的点，且AE平分∠BAC，BE＝CF，P为线段AC上的动点，记PD+PF的最小值为m，若正方形边长为√2，则m2的值为（）A．6﹣4√2B．8﹣4√2C．8+4√2D．6+4√2【变式47】如图，点E是边长为12的正方形ABCD边BC上的一点，BE＝5，点F在该正方形的边上运动，当BF＝AE时，设线段AE与线段BF相交于点H，则BH的长等于．【变式48】如图，E是正方形ABCD一边CD上的中点，AB＝4，动点P从A→B→C→D在正方形的边上运动，当△P AE为等腰三角形时，则AP的长为．。