三角形的中线角平分线高
- 格式:doc
- 大小:86.00 KB
- 文档页数:2

§5.1.3三角形的高、中线与角平分线1、[教学目标]基于上述对教材地位与作用的分析,结合学生已有的认知水平的年龄特征,制定本节如下的教学目标:(1)知识与技能目标:通过观察、画、折等实践操作、想像、推理、交流等过程,认识三角形的高线、角平分线、中线;会画出任意三角形的高线、角平分线、中线,通过画图、折纸了解三角形的三条高线、三条角平分线、三条中线会交于一点.(2)过程与方法目标:经历画、折等实践操作活动过程,发展学生的空间观念,推理能力及创新精神.学会用数学知识解决实际问题能力,发展应用和自主探究意识,并培养学生的动手实践能力.(3)情感与态度目标:通过对问题的解决,使学生有成就感,培养学生的合作精神,树立学好数学的信心.2、教学重点:能够正确地画出三角形的“高”、“角平分线”和“中线”,并理解它们概念的含义、联系和区别.3、教学难点:在钝角三角形中作高,理解高所在直线交于一点.[教学过程]本节课按照“创设情境,引入新课”——“合作交流,探求新知”——“拓展创新,挑战自我”——“课堂小结,感悟反思”——“走出课堂,应用数学”的流程展开.(每一个同学准备一个锐角三角形的纸片)你能画出这个三角形的三条高吗?你能用折纸的方法得到它们吗?从这三条高中你发现了什么?(这三条高之间有(可以反过来画好高后,找哪条边上高)=如果一个三角形的三条高的交点恰是三角形的一个顶边上高的是().你能画出三角形的所有中线吗?观察你们所作的图形,你又有哪些发现?与同伴交流.(分组合作交流)CD= , AF=,按图所示的方法折叠,和∠2两部分.观察1.三角形角平分线定义:三角形的角平分线:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形(准备三个三角形)你能分别画出或折出这三个三角形的角平分线。


三角形的高,中线,角平分线听评课三角形是几何学中的一种基本图形,具有丰富的性质和特点。
在三角形的研究中,高、中线和角平分线是非常重要的概念和性质。
本文将分别介绍三角形的高、中线和角平分线,并探讨它们的几何性质和应用。
一、三角形的高在三角形ABC中,如果从顶点A向底边BC作一条垂线,垂足为D,则AD就是三角形ABC的高。
三角形的高具有以下几个重要性质:1. 高与底边的关系:高AD是底边BC的垂线段,所以AD⊥BC(垂直)。
这意味着高与底边之间的夹角为90度。
2. 高的长度比例:在直角三角形ABC中,高AD与斜边AC和AB的关系满足勾股定理,即AD² = AC² - CD²和AD² = AB² - BD²。
这意味着高的长度与斜边的长度有一定的比例关系。
3. 高的位置关系:三角形的高可以位于内部、外部或边上。
如果高在三角形内部,那么它与三角形的三条边都有交点;如果高在三角形外部,那么它与三角形的某条边延长线有交点;如果高在三角形的边上,那么它与另外两条边的延长线有交点。
二、三角形的中线在三角形ABC中,如果从顶点A向底边BC作一条中线,中点为E,则AE就是三角形ABC的中线。
三角形的中线具有以下几个重要性质:1. 中线与底边的关系:中线AE可以被等分为两部分,即AE = CE。
这意味着中线与底边的长度存在一定的比例关系。
2. 中线的交点:三角形的三条中线交于一点,称为三角形的重心G。
重心G是三角形内部的一个点,它到三角形的三个顶点的距离相等。
3. 中线的位置关系:三角形的中线可以位于内部、外部或边上。
如果中线在三角形内部,那么它与三角形的三条边都有交点;如果中线在三角形外部,那么它与三角形的某条边平行且距离相等;如果中线在三角形的边上,那么它与另外两条边平行且距离相等。
三、三角形的角平分线在三角形ABC中,如果从顶点A作一条线段AD,使得∠BAD = ∠CAD,则AD就是角BAC的角平分线。

《11.1.2三角形的高、中线、角平分线》一、学习目标1.认识并会画出三角形的高线,利用其解决相关问题;2.认识并会画出三角形的中线,利用其解决相关问题;3.认识并会画出三角形的角平分线,利用其解决相关问题;二、导学指导与检测导学导学检测及课堂展示自主探究1、三角形的高(1)如图1,过A点作BC边所在直线的垂线AD,垂足为D,则叫做三角形的高.注意:三角形的高是一条线段;说三角形的高时,一定要指明是哪条边上的高.像上面,线段AD是BC边上的高.(2)要会“数学语言”:如上图,已知AD是⊿ABC边BC上的高,则 = =90O(3)任一个三角形都有三条高,三角形三条高的位置会因三角形形状的不同而有所不同。
分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高,观察高与三角形的位置关系。
(注意:作三角形的某边的高需要过这边的对角顶点向这边所在直线作垂线,故作钝角三角形两短边的高时,就需要延长这两短边。
)巩固应用:下列各个图形中,哪一个图形中AD是△ABC的高( )三角形的中线2. 如图,按下列步骤画△ABC 的中线:(1)量出BC 的长度,找BC 的中点D ,使BD = =。
(2)连接AD ,则线段AD 就叫做△ABC 的边BC 上的中线。
(3)三角形都有三条中线。
分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的中线, 观察中线与三角形的位置关系。
巩固应用:如右图,D 、E 是边AC 的三等分点,图中有 个三角形,BD 是三角形 中 边上的中线,BE 是三角形 中边________ 上的中线。
三角形的角平分线如图,按下列步骤画△ABC 的角平分线:(1)量出∠BAC 的度数,过点A 作线段AE 使∠BAE=∠CAE=21∠BAC , 且与BC 相交于点E 。
(2)则线段AE 就叫做△ABC 的一条角平分线。
(3)三角形都有三条角平分线。
分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的角 平分线,观察角平分线与三角形的位置关系。
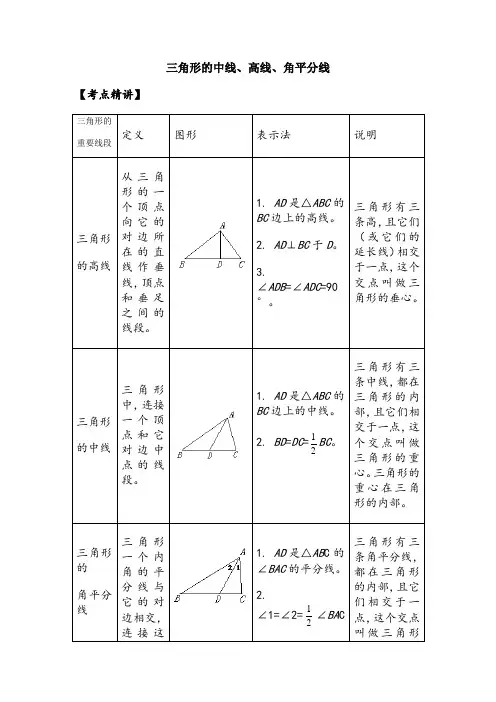
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段。
1. AD是△ABC的BC边上的高线。
2. AD⊥BC于D。
3.∠ADB=∠ADC=90°。
三角形有三条高,且它们(或它们的延长线)相交于一点,这个交点叫做三角形的垂心。
三角形的中线三角形中,连接一个顶点和它对边中点的线段。
1. AD是△ABC的BC边上的中线。
2. BD=DC=12BC。
三角形有三条中线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的重心。
三角形的重心在三角形的内部。
三角形的角平分线三角形一个内角的平分线与它的对边相交,连接这1. AD是△AB C的∠BAC的平分线。
2.∠1=∠2=12∠BA C三角形有三条角平分线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形个角的顶点与交点之间的线段。
的内心。
三角形的内心在三角形的内部。
【典例精析】例题1 如图,是甲、乙、丙、丁四位同学画的钝角△ABC 的高BE ,其中画对的是_______。
甲 乙 丙 丁思路导航:根据三角形的高是过一个顶点向对边引垂线,顶点与垂足之间的线段是该三角形的高,对各图形作出判断。
答案:丁点评:这是学生在画图时的一个易错点,通过本题理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边。
这道题是过B 点,垂直于AC 边。
例题 2 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是______。
思路导航:根据等腰三角形的性质和已知条件求出腰长和底边长,然后根据三边关系进行讨论,即可得出结论。
答案:设等腰三角形的腰长是x cm ,底边是y cm 。
根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+212122x y x x 或⎪⎪⎩⎪⎪⎨⎧=+=+122212x y x x , 解得:⎩⎨⎧==178y x 或⎩⎨⎧==514y x根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去。

三角形及其角平分线、中线和高线知识导引1、三角形的有关概念:定义:由不在通一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
外角:三角形一条边的延长线和另一条相邻的边组成的角。
三角形的中线:连结三角形的一个顶点与该顶点的对边中点的线段,叫做三角形的中线。
三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线。
三角形的角平分线:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
注意:三角形的中线、高线、角平分线都是线段。
2、三角形的边角关系:边与边的关系:三角形的任意一边大于另外两边之差,并小于另外两边之和。
角与角的关系:三角形的内角和等于180°,外角和等于360°;三角形的一个外角等于和它不相邻的两个内角的和,且大于任何一个和它不相邻的内角。
边与角的关系:在一个三角形中,等角对等边,等边对等角,大角对大边,大边对大角。
3三角形的分类:按角分:三角形可分为锐角三角形、直角三角形、钝角三角形。
按边分:三角形可分为不等边三角形、等腰三角形。
典例精析例1:现有2cm,4cm,5cm,8cm长的四根木棒,任意选取三根组成一个三角形,那么可以组成三角形的个数为()A、1个B、2个C、3个D、4个例2:如图,AD是△ABC的角平分线,AE是BC边上的高线,∠B=20°,∠C=40°,求∠DAE 的度数。
例3:如图所示,平面上的六个点A、B、C、D、E、F构成一个封闭的折线图形。
求∠A+∠B +∠C+∠D+∠E+∠F的值。
例3—1:求如图1所示图形中∠A+∠B+∠C+∠D+∠E 的大小。
例3—2:如图所示,(∠1+∠2-∠3)+(∠4+∠5-∠6)+(∠7+∠8-∠9)=例4:如图所示,在△ABC 中,∠ABC 的平分线与∠ACB 的外角平分线交于点D ,且∠D=30°,求∠A 的度数。


三角形的高、中线与角平分线三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 三角形的中线。
三角形中,连结一个顶点和它对边中点的线段。
三角形角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段。
D C B A D C B A 21D CB A∵AD 是△ABC 的BC 的高线.∵AE 是△ABC 的BC 的中线.∵AM 是△ABC 的∠BAC 的平分线. ∴AD⊥___ ∴BE=EC=12____. ∴∠1=∠2=12∠_____.∴∠ADB=∠AD C=____°.1.以下说法错误的是( )A .三角形的三条高一定在三角形内部交于一点B .三角形的三条中线一定在三角形内部交于一点C .三角形的三条角平分线一定在三角形内部交于一点D .三角形的三条高可能相交于外部一点2.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,•那么这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .不能确定3.如图1,BD=12BC ,则BC 边上的中线为______,△ABD 的面积=_____的面积.(1) (2) (3)4.如图2,△ABC 中,高CD 、BE 、AF 相交于点O ,则△BOC•的三条高分别为线段________.5.下列图形中具有稳定性的是( )A .梯形B .菱形C .三角形D .正方形6.如图3,AD 是△ABC 的边BC 上的中线,已知AB=5cm ,AC=3cm ,求△ABD•与△ACD 的周长之差. 7.如图,∠BAD=∠CAD ,AD ⊥BC ,垂足为点D ,且BD=CD .• 可知哪些线段是哪个三角形的角平分线、中线或高? 8.在等腰三角形ABC 中,AB=AC ,一腰上的中线BD 将这个等腰三角形的周长分为15和6两部分,求该等腰三角形的腰长及底边长. 9.有一块三角形优良品种试验基地, 如图所示,•由于引进四个优良品种 进行对比试验,需将这块土地分成面 积相等的四块,请你制定出两种以上 的划分方案供选择(画图说明). 10.如图,在△ABC 中,D 、E 分别是BC 、AD 的中点,S △ABC =4cm 2,求S △ABE . 1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。

教学过程(要求:思路清晰,层次分明,环环相扣,反馈及时,突出学生主题地位)通过画图我们可以发现三角形的三条高相交于一点(垂心)。
锐角三角形的垂心在三角形内直角三角形的垂心是三角形的直角顶点钝角三角形的垂心在三角形外部2、三角形的中线在三角形中,连接一个顶点与它对边中点的线段, 叫做这个三角形这边的中线.如图,连结△ABC的顶点A和它的对边BC的中点D,所得线段AD就是△ABC的边BC上的中线。
连接△ABC的顶点B和它的对边AC的中点E,所得线段BE就是△ABC 的边AC上的中线。
连接△ABC的顶点C和它的对边AB的中点F,所得线段CF就是△ABC 的边AB上的中线。
知道了三角形中线的概念,我们看上图:∵AD是△ABC的中线∴BD=CD=1/2BC或BC=2BD=2CD在图中你还能找出那些相等的线段?三角形的三条中线相交于一点。
三角形的三条中线的交点叫做三角形的重心。
如果三角形是直角三角形、钝角三角形,上面的结论还成立吗?请画图回答。
上面的结论还成立。
补充:如图,在△ABC中,AE,AD分别是BC边上中线和高,(1)说明△ABE的面积与△AEC的面积有何关系?(2)你有什么发现?同高等底的两个三角形的面积________.三角形的中线把三角形分成两个面积_______的三角形。
3、三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段就是三角形的一条角平分线。
画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD就是△ABC的一条角平分线。
画∠B的平分线BE,交∠B所对的边AC于点E,所得线段BE就是△ABC的一条角平分线画∠C的平分线CF,交∠C所对的边AB于点F,所得线段CF就是△ABC的一条角平分线∵AD是△ABC的角平分线∴∠1=∠2=1/2∠BAC∴∠BAC=2∠1=2∠2CDF EABAB DE CCDF EAB请你在图中画出另两个角的平分线,看看有什么发现?三角形三条角平分线相交于一点(内心)。


第2课时三角形的高、中线与角平分线一、教学目标1.知识目标:认识三角形的高.中线与角平分线.2.能力目标:会用工具准确画出三角形的高.中线与角平分线, 通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于一点.3.情感目标:采用自学与小组合作学习相结合的方法,培养自己主动参与.勇于探究的精神.二、教学重点、难点重点:1.了解三角形的高.中线与角平分线的概念, 会用工具准确画出三角形的高.中线与角平分线.2.了解三角形的三条高.三条中线与三条角平分线分别交于一点.难点:1.三角形平分线与角平分线的区别,三角形的高与垂线的区别.2.钝角三角形高的画法.3.不同的三角形三条高的位置关系.三、教学过程(一)激趣导入我们已经知道什么是三角形,也学过三角形的高.三角形的主要线段除高外,还有中线和角平分线值得我们研究.(二)预习定标迅速浏览教材P4——P5练习之前的内容,说说本节课我们学习的内容将会是什么?(三)合作达标活动一:画一画,想一想请你在图中画出△ABC 的一条高并说说你画法. D C B A从△ABC 的顶点A 向它所对的边BC 所在的直线画垂线,垂足为D ,所得线段AD 叫做△ABC 的边BC 上的高,表示为AD ⊥BC 于点D.注意:高与垂线不同,高是线段,垂线是直线.请你再画出这个三角形AB ,AC 边上的高,看看有什么发现?三角形的三条高相交于一点.如果△ABC 是直角三角形.钝角三角形,上面的结论还成立吗?现在我们来画钝角三角形三边上的高,如图.显然,上面的结论成立.请你画一个直角三角形,再画出它三边上的高.上面的结论还成立.活动二:读一读,说一说如图,我们把连结△ABC 的顶点A 和它的对边BC 的中点D ,所得线段AD 叫做△ABC 的边BC 上的中线,表示为BD=DC 或BD=DC =1/2BC 或2BD=2DC=BC.D C B AABCO D E F请你在图中画出△ABC 的另两条边上的中线,看看有什么发现?三角的三条中线相交于一点。
三角形的中线,角平分线,高线的定义
三角形的中线、角平分线和高线是三角形中的三条重要线段,它们各自具有独特的性质和定义。
以下是它们的定义:
1.中线:
o定义:中线是从一个角的顶点出发,平分对边(或其延长线)的线段。
o性质:中线将相对边分为两段相等的部分。
o定理:三角形的中线与相对边上的中点重合。
2.角平分线:
o定义:角平分线是从一个角的顶点出发,将相对边分为两段相等的线段。
o性质:角平分线将相对边分成两段相等的部分,并且与相对边的中线重合。
o定理:角平分线上的点到这个角的两边的距离相等。
3.高线:
o定义:高线是从一个角的顶点出发,垂直于对边(或其延长线)的线段。
o性质:高线将对应的底边分为两段相等的部分。
o定理:高线所在的直线与相对底边垂直。
三角形的高中线和角平分线的性质三角形是几何学中最基本且重要的图形之一,它有许多性质和定理。
在这篇文章中,我们将讨论三角形中高中线和角平分线的性质和特点。
1. 高中线的性质在任意三角形中,高是从一个顶点到对边的垂直线段。
三角形的任意两条高线都相交于同一点,该点被称为垂心。
这是三角形的一个重要性质。
2. 高中线的长度关系对于任意三角形ABC,设AD、BE和CF分别是三角形ABC的三条高线(D、E和F分别是三角形ABC对边上的高线足点)。
根据高的性质,D、E和F是共线的,且它们交于垂心H。
我们可以证明以下结论:(1)在任意三角形中,垂心到顶点的距离等于顶点到对边的距离,即DH=EH=FH。
(2)垂心将三角形的三条高线等分,即AH=DH=EH=FH。
3. 角平分线的性质角平分线是从一个角的顶点到对边上的点,将该角分成两个相等的角。
在三角形中,任意两条角平分线相交于同一点,该点被称为内心。
这也是三角形的一个重要性质。
4. 角平分线和边的关系对于任意三角形ABC,设AD、BE和CF分别是三角形ABC的三条角平分线(D、E和F分别是三角形ABC的顶点所在边上的点)。
根据角平分线的性质,D、E和F是共线的,且它们交于内心I。
我们可以证明以下结论:(1)三角形的内心到三条边的距离相等,即ID=IE=IF。
(2)内心到三边的距离和等于内心到三边所对应的角的角平分线长度之和,即ID+IE+IF=AD+BE+CF。
5. 高中线和角平分线的关系在某些三角形中,高线和角平分线有一些特殊的关系。
我们来看以下两个例子:(1)等腰三角形:对于等腰三角形ABC(AB=AC),由于两条边相等,所以角平分线也是高线,且垂心和内心重合。
(2)直角三角形:对于直角三角形ABC(∠ABC=90°),角平分线等于斜边的一半,且角平分线与斜边垂直。
综上所述,我们介绍了三角形中高中线和角平分线的性质和特点。
高中线通过三角形的一个顶点,垂直于对边,其长度有一定的关系;角平分线从一个角的顶点出发,分割该角成两个相等的角,且和其他角平分线相交于内心。
“目标引领 一•五••九”课堂教学学案
二、认定学习目标:
(一)、自主学习:
1.什么叫角平分线?如何画一个角的平分线?
2.已知A 、B 分别是直线l 上和直线l 外一点,分别过点A 、点B 画直线l 的垂线. l
3.三角形按角分类可分为哪几种?
(二)、合作探究
1.三角形的中线:三角形的一个顶点与它的对边中点的连线叫三角形的中线. 问:三角形有几条中线?若已知AD 是三角形的中线,你可得到什么结论?
2.三角形的角平分线:三角形内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线.
问:三角形有几条角平分线?三角形的角平分线和角平分线有什么不同?
3.三角形的高:过三角形顶点作对边的垂线,垂足与顶点间的线段叫三角形的高.
图8.2.5
(三)、评析精讲:
例1.如图△ABC,边BC上的高画得对吗?为什么?
4.做一做:让学生拿出昨天做的三个锐角三角形. (1)分别画出中线、角平分线、高.
(2)你能用折纸的办法得到这些线段吗?试一试.
(只要求折出一条中线、一条高,一条角平分线)
(3)把锐角三角形换成直角三角形、钝角三角形再试一试.
将你的结果与同伴进行交流.
三、强化学习目标:
(1)一个三角形中三条中线(高、角平分线)之间的位置关系怎样?
[三条中线交于一点,三条角平分线交于一点,三条高所在的直线交于一点]
(2)一个三角形的三条中线(角平分线)的交点与三角形有怎样的位置关系?
[三条中线(角平分线)相交于一点,这一点在三角形内部]
(3)直角三角形的三条高,它们有怎样的位置关系?钝角三角形呢?
[直角三角形有一条高在三角形内部,另外两条就是直角三角形的两条直角边,三条高的交点就是直角三角形的直角顶点,钝角三角形有一条高在形内,两条高在形外,三条高所在的直线的交点在形外.]
(4)你能折出钝角三角形的三条高吗?
四、感悟学习目标
1、本节课我学习的知识有:
2、节课我疑惑的知识点是:
3、本节课的学习我明白了哪些事理?要成为最好的自己,我还需在哪些方面努力?。