几何图形的折叠问题

七年级折叠问题解题技巧一、折叠问题中的基本性质与关系1. 折叠性质在折叠过程中，折叠前后的图形全等。

这意味着对应边相等，对应角相等。

例如，将一个三角形沿着某条直线折叠，折叠后的三角形与原三角形的对应边长度不变，对应角的大小也不变。

折痕是对应点连线的垂直平分线。

比如将矩形ABCD沿着EF折叠，使得点A与点C重合，那么EF就是AC的垂直平分线。

2. 常见的几何图形中的折叠三角形折叠例1：在△ABC中，∠C = 90°，将△ABC沿着直线DE折叠，使点A与点B 重合，若AC = 6，BC = 8，求折痕DE的长。

解析：因为点A与点B重合，所以DE是AB的垂直平分线。

先根据勾股定理求出AB=公式。

设AB中点为F，则AF=公式。

由于△ADE和△BDE全等，所以AD = BD。

设BD = x，则AD = x，CD = 8 x。

在Rt△ACD中，根据勾股定理公式，即公式，解得公式。

再根据相似三角形，△ADE∽△ABC，公式，即公式，解得DE=公式。

矩形折叠例2：矩形ABCD中，AB = 3，BC = 4，将矩形沿对角线AC折叠，求重叠部分（△AEC）的面积。

解析：因为矩形沿对角线AC折叠，所以△ADC≌△AEC。

设AE = x，则BE = 4 x。

在Rt△ABE中，根据勾股定理公式，即公式，解得公式。

所以公式。

二、解题步骤与技巧1. 步骤第一步：根据折叠性质确定相等的边和角。

这是解决折叠问题的基础，只有明确了这些关系，才能进一步进行计算。

第二步：设未知数。

通常根据所求的量或者与所求量相关的线段设未知数，然后利用勾股定理、相似三角形等知识建立方程。

第三步：求解方程。

通过解方程得到未知数的值，从而求出最终答案。

2. 技巧利用勾股定理在直角三角形中，折叠后常常会形成新的直角三角形，此时可以利用勾股定理建立方程求解。

如上述矩形折叠的例子中，在Rt△ABE中利用勾股定理求出AE的长度。

利用相似三角形当折叠后的图形与原图形存在相似关系时，利用相似三角形的对应边成比例来求解。

初中几何折叠问题的三种解法初中几何折叠问题的三种解法初中几何是数学中的一个重要分支，而折叠问题则是初中几何中常见的一种问题。

在这里，我们将介绍三种不同的方法来解决初中几何折叠问题。

方法一：手工模拟法手工模拟法是一种简单直观的方法。

它通过将纸张折叠成所需形状来解决问题。

步骤：1. 根据题目给出的图形，画出所需大小和比例的图形。

2. 将纸张按照比例剪成相应大小。

3. 按照题目要求，将纸张进行折叠，直到得到所需形状。

4. 计算所需参数并得出答案。

优点：手工模拟法操作简单易懂，适合初学者使用。

同时也能够帮助学生更好地理解折叠问题的本质。

缺点：手工模拟法需要较长时间完成，并且需要精确测量和折叠。

同时也容易出现误差和偏差。

方法二：平面几何法平面几何法是一种基于平面几何知识来解决问题的方法。

它通过利用图形相似性和对称性来计算所需参数。

步骤：1. 根据题目给出的图形，画出所需大小和比例的图形。

2. 根据平面几何知识，计算所需参数，如角度、长度等。

3. 得出答案。

优点：平面几何法具有计算速度快、精度高等特点。

同时也能够帮助学生更好地理解平面几何知识的应用。

缺点：平面几何法需要学生具备一定的数学基础，并且需要对图形相似性和对称性有深入理解。

同时也容易出现计算错误和漏算情况。

方法三：三维几何法三维几何法是一种基于立体几何知识来解决问题的方法。

它通过利用立体图形的投影和相似性来计算所需参数。

步骤：1. 根据题目给出的图形，画出所需大小和比例的图形。

2. 利用三维几何知识，将立体图形投影到二维平面上，并计算所需参数，如角度、长度等。

3. 得出答案。

优点：三维几何法具有计算速度快、精度高等特点。

同时也能够帮助学生更好地理解立体几何知识的应用。

缺点：三维几何法需要学生具备一定的数学基础，并且需要对立体图形的投影和相似性有深入理解。

同时也容易出现计算错误和漏算情况。

结论：初中几何折叠问题可以通过多种方法来解决，其中手工模拟法、平面几何法和三维几何法是常见的三种方法。

DE中考数学中的折叠问题为了考查学生的数、形结合的数学思想方法和空间想象能力，近几年来中考中常出现折叠问题。

几何图形的折叠问题，实际是轴对称问题。

处理这类问题的关键是根据轴对称图形的性质，搞清折叠前后哪些量变了，哪些量没变，折叠后有哪些条件可利用。

所以一定要注意折叠前后的两个图形是全等的。

即对应角相等，对应线段相等。

有时可能还会出现平分线段、平分角等条件。

这一类问题，把握住了关键点，并不难解决。

例1 （成都市中考题）把一张长方形的纸片按如图所示的方式折叠， EM 、FM 为折痕，折叠后的C 点落在'B M 或'B M 的延长线上，那么∠EMF 的度数是（ ）A 、85°B 、90°C 、95°D 、100°分析与解答：本题考查了有关折叠的知识。

由题意可知：∠BME=∠'EMC ，∠CMF=∠'FMC ，''180BMC CMC ∠+∠=°，又'C M 与'B M 重合，则∠EMF=∠'EMC +∠'FMC =''11()18022BMC CMC ∠+∠=⨯°= 90°，故选B 。

例2 （武汉市实验区中考题）将五边形ABCDE 纸片按如图的方式折叠，折痕为AF, 点E 、D 分别落在'E 、'D 。

已知∠AFC=76°，则'CFD ∠等于（ ）A 、31°B 、28°C 、24°D 、22°分析与解答：本题同样是考查了折叠的知识。

根据题意得：'AFD AFD ∠=∠=180°-76°=104°，则'CFD ∠=104°-76°=28°，故选B 。

例3（河南省实验区中考题）如图，把矩形纸片OABC 放入平面直角坐标系中，使OA 、OC 分别落在x 轴、y 轴上，连结OB ，将纸片OABC 沿OB 折叠，使点A 落在点'A 的位置，若1tan 2BOC ∠=，则点'A 的坐标为 。

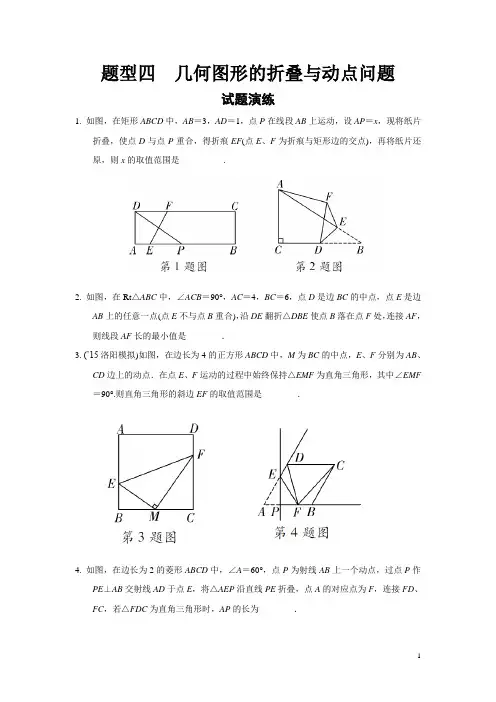
题型四几何图形的折叠与动点问题试题演练1. 如图，在矩形ABCD中，AB＝3，AD＝1，点P在线段AB上运动，设AP＝x，现将纸片折叠，使点D与点P重合，得折痕EF(点E、F为折痕与矩形边的交点)，再将纸片还原，则x的取值范围是__________.2. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点D是边BC的中点，点E是边AB上的任意一点(点E不与点B重合)，沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF长的最小值是________．3. (’15洛阳模拟)如图，在边长为4的正方形ABCD中，M为BC的中点，E、F分别为AB、CD边上的动点．在点E、F运动的过程中始终保持△EMF为直角三角形，其中∠EMF ＝90°.则直角三角形的斜边EF的取值范围是________．4. 如图，在边长为2的菱形ABCD中，∠A＝60°，点P为射线AB上一个动点，过点P作PE⊥AB交射线AD于点E，将△AEP沿直线PE折叠，点A的对应点为F，连接FD、FC，若△FDC为直角三角形时，AP的长为________．5. 如图，正方形ABCD的边长为2，∠DAC的平分线AE交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ＋PQ的最小值为________．6. 如图，在矩形ABCD中，AD＝3，AB＝4，点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D′落在矩形的对角线上时，DE的长为________．7. 如图，矩形纸片ABCD中，AB＝8，将纸片折叠，使顶点B落在边AD上，对应点为点E，若BG＝10，则折痕FG的长为________．8. 如图，在Rt△ABC中，∠ABC＝90°，AC＝10，BC＝8，AD是∠BAC的平分线，点E是斜边AC上的一点，且AE＝AB，沿△DEC的一个内角平分线折叠，使点C落在DE所在直线上，则折痕的长度为________．9. (’15商丘模拟)如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点E是AB边上一动点，过点E作DE⊥AB交AC边于点D，将∠A沿直线DE翻折，点A落在线段AB 上的点F处，当△BCF为等腰三角形时，AE的长为________．10. (’15郑州模拟)如图，在矩形ABCD中，AD＝6，CD＝4，AD的中点为E，点F是AB边上一点(不与A、B重合)，连接EF，把∠A沿EF折叠，使点A落在点G处，连接CG.则线段CG的取值范围是________．11. (’15江西)如图，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△P AB为直角三角形时，AP的长为________．12. 如图，在矩形ABCD中，AB＝12，BC＝8，点E是边BC上一动点，把△DCE沿DE折叠得△DFE，射线DF交直线CB于点P，当△AFD为等腰三角形时，DP的长为_____【答案】1. 1≤x≤3【解析】通过观察图形，可得当点E与点A重合时AP最小，则AP＝EP＝AD ＝1；当点P与点B重合时，AP最大，则AP＝3，∴1＜AP≤3，则x的取值范是1≤x≤3.2. 2【解析】由题意得：DF＝DB，∴点F在以D为圆心，BD为半径的圆上，作⊙D，连接AD交⊙D于点F，此时AF值最小；∵点D是边BC的中点，∴CD＝BD＝3；而AC＝4.由勾股定理得：AD2＝AC2＋CD2∴AD＝5，而FD＝3，∴F A＝5－3＝2，即线段AF长的最小值是2.3. 4≤EF≤5【解析】∵点M为BC的中点，正方形ABCD的边长为4，∴BM＝CM＝2，∵∠EMF＝90°，∴∠BME＋∠CMF＝90°，∵∠CFM＋∠CMF＝90°，∴∠BME＝∠CFM，又∵∠B＝∠C＝90°，∴△BME∽△CFM，∴BMCF＝BECM，∴BE·CF＝BM·CM＝2×2＝4，∵CF最大时为4，此时BE＝1，BE最大时为4，此时CF＝1，∴0≤|CF－BE|≤3，过点E 作EG⊥CD于点G，则EG＝BC＝4，在Rt△EFG中，EF2＝EG2＋FG2＝16＋(CF－BE)2，∴16≤EF2≤16＋9，∴4≤EF≤5.4. 12或32 【解析】根据题意可得△FDC 为直角三角形时分三种情况考虑：(1)如解图①，当∠FDC ＝90°时，DF ⊥AB ，在△AFD 中，∠A ＝60°，AD ＝2，∴AF ＝1，AP ＝12；(2)如解图②，当∠DCF ＝90°时，CF ⊥AB ，在△CFB 中，∠CBF ＝60°，BC ＝2，∴BF ＝1，AF ＝3，AP ＝32；(3)当∠DFC ＝90°，不存在．综上可知AP 的值为12或32.5. 2 【解析】如解图，作D 关于AE 的对称点D ′，则D ′落在对角线AC 上，过点D ′作 D ′P ′⊥AD 于点P ′，∴D ′P ′即为DQ ＋PQ 的最小值，∵DD ′⊥AE ，∴∠AFD ＝∠AFD ′，∵AF ＝AF ，∠DAF ＝∠D ′AF ，∴△DAF ≌△D ′AF ，∴AD ＝AD ′＝2，∵四边形ABCD 是正方形，∴∠DAD ′＝45°，∴AP ′＝P ′D ′，∴在Rt △AP ′D ′中，P ′D ′2＋AP ′2＝AD ′2， AD ′2＝4，∴P ′D ′＝2，即DQ ＋PQ 的最小值为 2.6. 32或94【解析】分两种情况进行讨论，设DE ＝x .ⅰ)D ′落在AC 上，如解图1，在Rt △ED ′C 中，EC ＝4－x ，D ′C ＝AC －AD ′＝5－3＝2，ED ′＝x ，根据ED ′2＋D ′C 2＝EC 2可得x 2＋22＝(4－x )2，解得x ＝32；ⅱ)D ′落 在BD 上，如解图2，设DD ′交AE 于F 根据轴对称性质可知AE 垂直平分DD ′.在Rt △DF A 中，sin ∠ADF ＝AF AD ，∵sin ∠ADF ＝sin ∠ADB ＝AB BD ＝45，∴AF AD ＝45，又∵AD ＝3，∴AF ＝125，∴DF ＝95，又∵∠DEF ＝∠ADF ，∴sin ∠DEF ＝sin ∠ADF ＝45，∴DF DE ＝45，即95DE ＝45，∴DE ＝95×54＝94.综上DE 的长为32或94.7. 55或45 【解析】分两种情况讨论：(1)如解图①，过点G 作GH ⊥AD 于点H ，则四边形ABGH 为矩形，∴GH ＝AB ＝8，由图形折叠可知△BFG ≌ △EFG ，∴EG ＝BG ＝10，∠B ＝∠FEG ＝90°，∴EH ＝6，AE ＝4，∠AEF ＋∠HEG ＝90°，∵∠AEF ＋∠AFE ＝90°，∴∠HEG ＝∠AFE ，又∵∠A ＝∠EHG ＝90°，∴△EAF ∽△GHE ，∴EF EG ＝AE GH，∴EF ＝5，∴FG ＝102＋52＝55；(2)如解图②，由图形的折叠可知四边形ABGF ≌四边形HEGF ，∴BG ＝EG ，AB ＝EH ，∠BGF ＝∠EGF ，∵EF ∥BG ，∴∠BGF ＝∠EFG ，∴∠EFG ＝∠EGF ，∴EF ＝EG ，∴BG ＝EF ，∴四边形BGEF 为平行四边形，∵EF ＝EG ，∴平行四边形BGEF 为菱形，连接BE ，∴BE 、FG 互相垂直平分．在Rt △EFH 中，EF ＝BG ＝10，EH ＝AB ＝8，由勾股定理可得FH ＝AF ＝6，∴AE ＝AF ＋EF ＝16，∴BE ＝AE 2＋AB 2＝85，∴BO ＝45，∴OG ＝BG 2－BO 2＝25，∵四边形BGEF 为菱形，∴FG ＝2OG ＝4 5.8. 1227或352【解析】在Rt △ABC 中，∠ABC ＝90°，AC ＝10，BC ＝8，∴AB ＝102－82＝6，则AE ＝6，EC ＝AC －AE ＝10－6＝4；∵AB ＝AE ，∠BAD ＝∠EAD ，AD ＝AD ，∴△ABD ≌△AED ，∴BD ＝DE ，∠B ＝∠AED ＝90°，设BD ＝x ，则DE ＝x ，CD ＝8－x ，∴x 2＋42＝(8－x )2，解得：x ＝3，∴CD ＝5，DE ＝3.(1)如解图①，若沿∠DEC 的角平分线EG 折叠，使点C 落在ED 延长线上F 点处，过G 分别作GM ⊥EC ，GN ⊥EF ，垂足分别为M 、N .∴GN＝GM ，∵S △DEC ＝12×3×4＝6，S △DEG ＝12×3·GN ＝32GN ，S △CEG ＝12×4·GM ＝2GM ，∴2GM ＋32GN ＝6，即2GN ＋32GN ＝6，解得：GN ＝127，故EG ＝1227；(2)如解图②，若沿∠EDC 的角平分线DG 折叠，使点C 落在DE 延长线上F 点处．∴CG ＝FG ，DC ＝DF ＝5，∵DE＝3，∴EF ＝2，设CG ＝y ，则FG ＝y ，EG ＝4－y ，∴(4－y )2＋22＝y 2，解得：y ＝52，∴EG＝4－52＝32，∵DE ＝3，∴DG ＝（32）2＋32＝94＋9＝352. 9. 1或54或710【解析】本题考查三角形的折叠，等腰三角形的性质求线段的长．在Rt △ABC 中，AC ＝4，BC ＝3，由勾股定理得AB ＝AC 2＋BC 2＝5.由折叠性质得AE ＝EF ，在△BCF 中，当BF ＝BC 时，有BF ＝AB －AF ＝AB －2AE ＝3，则AE ＝1; 当BF ＝CF 时，过BC 中点作AC 的平行线，交AB 于点F ，此时F 点满足题意，且AF ＝BF ＝52，则AE ＝54； 当CF ＝CB 时，如解图，过C 作CN ⊥AB 于点N .由等面积法得CN ＝AC ·BC AB ＝125.由△BCN ∽△BAC ，得BN BC ＝BC AB ，则BN ＝95.由等腰三角形三线合一性质得FN ＝BN ＝95，则AE ＝12AF ＝12(AB －BF )＝12×(5－185)＝710. 10. 2537＜CG ＜213 【解析】如解图所示，在Rt △ADC 中，AD ＝6，CD ＝4，∴AC ＝AD 2＋CD 2＝213，把∠A 沿EB 折叠，此时CG 最小，使点A 落在点G 处，连接AG ，DG ，∴∠EAG ＝∠EGA ，AE ＝EG ，∵AE ＝DE ，∴EG ＝ED ，∴∠ADG ＝∠EGD ，∴∠AGD ＝∠AGE ＋∠EGD ＝∠DAG ＋∠ADG ＝90°，∵AE ＝3，AB ＝4，∴BE ＝AE 2＋AB 2＝5，∵12AG ·BE ＝AE ·AB ，∴AG ＝245，在Rt △ADG 中，DG ＝AD 2－AG 2＝62－（245）2＝185，过G 点作MN ⊥AD ，∴∠AMG ＝∠AGD ＝90°，∵∠MAG ＝∠GAD ，∴△AMG ∽△AGD ，∴AM AG＝MG DG ＝AG AD ，即：AM 245＝MG 185＝2456，∴AM ＝9625，MG ＝7225，∵BN ＝AM ＝9625，MN ＝CD ＝4，∴CN ＝6－9625＝5425，GN ＝4－7225＝2825，在Rt △CNG 中，CG ＝CN 2＋GN 2＝2537.在Rt △ABC 中，AC ＝AB 2＋BC 2＝213，∴线段CG 的取值范围是2537＜CG ＜213.11. 2或23或27 【解析】由于点P 在射线CO 上运动，∴当△P AB 为直角三角形时，有三种情况：(1)当∠APB ＝90°时，①如解图①，当点P 在线段CO 上时，∵AB ＝BC ＝4，AO ＝BO ，∴AO ＝2，∴PO ＝AO ＝2，∵∠AOC ＝60°，∴△APO 是等边三角形，∴AP ＝AO ＝2；②如解图②所示，当点P 在CO 的延长线上时，∵AB ＝BC ＝4，AO ＝BO ，∠AOC ＝60°，∴OP ＝OA ＝OB ＝2，∵∠POB ＝∠AOC ＝60°，∴△POB 是等边三角形，即PB ＝OB ＝2，∴AP ＝AB 2－PB 2＝42－22＝23；(2)当∠ABP ＝90°时，如解图③所示，∵AB ＝BC ＝4，AO ＝BO ，∴AO ＝BO ＝2，又∵∠BOP ＝∠AOC ＝60°，∠ABP ＝90°，∴BP ＝23，在Rt △APB 中，AP ＝AB 2＋PB 2＝42＋（23）2＝27；∴AP 的长度为2或23或27.12. 92或4877【解析】∵四边形ABCD 是矩形，∴AD ＝BC ＝8，AB ＝DC ＝12，AD ∥BC ，∠C ＝90°.∵把△DCE 沿DE 折叠得△DFE ，∴DC ＝DF ＝12.∵AD ≠DF ，∴△AFD 为等腰三角形只有两种情况： (1)当AF ＝FD ＝12时，如解图①，过点F 作FM ⊥AD于点M ，∴AM ＝MD ＝4，在Rt △MDF 中，由勾股定理，得MF ＝122－42＝82，∵AD ∥BC ，∴∠MDF ＝∠DPC .∵∠DMF ＝∠C ＝90°，∴△MDF ∽△CPD ，∴MF CD ＝FD PD ，即：8212＝12PD，解得PD ＝92； (2)当AD ＝AF ＝8时，如解图②，DF 的延长线交CB 的延长线于点P ，过点A 作AN ⊥DF 于点N, ∴FN ＝ND ＝6，在Rt △AND 中，由勾股定理，得AN ＝82－62＝27，∵AD ∥BC ，∴∠ADN ＝∠DPC ，∵∠AND ＝∠C ＝90°， ∴△AND ∽△DCP ，∴AN CD ＝AD PD ，即：2712＝8PD ，解得PD ＝4877.综上所述，DP 的长为92或4877。

常见几何图形的折叠问题图形的折叠是图形变换的一种，折叠型问题的立意新颖，变化巧妙，是近几年中考中的热点问题，主要考察学生的探究能力，空间想象能力，抽象思维能力及逻辑推理能力。

体现的是教材中的轴对称问题，在解决这类问题中，运用的知识点比较多，综合性强，如轴对称性、全等思想、相似思想、勾股定理、代换思想等，是培养学生识图用图能力，灵活运用数学知识解决问题能力的一条非常有效的途径。

折叠操作就是将图形的一部分沿着一条直线翻折1800，使它与另一部分图形在这条直线的同旁与其重叠或不重叠，其中“折”是过程，“叠”是结果. 折叠问题的实质是图形的轴对称变换，折叠更突出了轴对称问题的应用. 所以在解决有关的折叠问题时可以充分运用轴对称的思想和轴对称的性质。

折纸中所蕴含着的丰富数学知识备受中考命题者的青睐，设计了许多别具创意的折叠问题，现采撷其中较有代表性的试题，予以例析．一、三角形中的折叠例1 如图1，直角三角形纸片ABC ，∠C=90º，AC=6，BC=8，折叠△ABC 的一角，使点B 与A 点重合，展开得折痕DE ，求BD 的长．功能分析：此题主要运用勾股定理解决折叠问题，往往融方程与几何图形于一体，具有较强的综合性。

解法研究: 由折叠可知，△ADE ≌△BDE ．所以AD=BD ．于是，在Rt △ACD 中，由勾股定理建立方程，求出AD 的长即可．设BD=x ，则AD=x ，CD=8－x ．在Rt △ACD 中，由勾股定理，得AC 2+CD 2= AD 2，所以62+(8－x)2= x 2，解得x=425．所以BD 的长为425． 二、特殊四边形中的折叠 1. 矩形中的折叠例2 如图2，将矩形ABCD 沿着直线BD 折叠，使点C 落在1C 处，B 1C 交AD 于E ，AD =8,AB =4,求△BED 的面积.功能分析：由折叠后的图形与原图形全等，从而可知△BCD ≌△B 1C D ,则易得BE =DE ..在Rt △ABE 中，用勾股定理先算出BE 的长，再在Rt △BEF 中，用勾股定理求出EF 的长，即可求出△BDE 的面积.折叠问题常结合全等三角形和等腰三角形来解决． 矩形的折叠常与直角三角形有关，选择一个直角三角形，运用勾股定理来解是常用的方法．解法研究：在矩形ABCD 中，AD ∥BC , ∴∠2=∠3.当矩形ABCD 沿着直线BD 折叠后，△B 1C D 与△BCD 关于直线BD 对称， ∴∠1=∠2, ∴∠3=∠1, ∴BE =ED .图2作EF ⊥BD 于F ,则BF =21BD ,BD =.544822=+ 设BE =x . ∵BE =ED , ∴AE =8- x .在Rt △ABE 中,,)(22284x x =-+ ∴x =5. 在Rt △BEF中,,)(,)(22222252552+=+=EF EF x∴EF =5,∴.1021=⋅=∆EF BD S BDE 例3 如图3（1），矩形纸片ABCD 的边长分别为()a b a b <，．将纸片任意翻折（如图3（2）），折痕为PQ ．（P 在BC 上），使顶点C 落在四边形APCD 内一点C '，PC '的延长线交直线AD 于M ，再将纸片的另一部分翻折，使A 落在直线PM 上一点A '，且A M '所在直线与PM 所在直线重合（如图3（4））折痕为MN ． 猜想两折痕PQ MN ，之间的位置关系，并加以证明．功能分析：解决本题的关键在于能否抓住互相重合部分的特点，这要求同学们掌握折痕是对称轴这一性质。

初中数学中的折叠问题折叠问题（对称问题）是近几年来中考出现频率较高的一类题型，学生往往由于对折叠的实质理解不够透彻，导致对这类中档问题失分严重。

本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析，从中抽象出基本图形的基本规律，找到解决这类问题的常规方法。

其实对于折叠问题，我们要明白：1、折叠问题（翻折变换）实质上就是轴对称变换．2、折叠是一种对称变换，它属于轴对称．对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、对于折叠较为复杂的问题可以实际操作图形的折叠，在画图时，画出折叠前后的图形，这样便于找到图形之间的数量关系和位置关系．4、在矩形（纸片）折叠问题中，重合部分一般会是一个以折痕为底边的等腰三角形5、利用折叠所得到的直角和相等的边或角，设要求的线段长为x，然后根据轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解．一、矩形中的折叠1．将一张长方形纸片按如图的方式折叠，其中BC，BD为折痕，折叠后BG和BH在同一条直线上，∠CBD= 度．BC、BD是折痕，所以有∠ABC = ∠GBC，∠EBD = ∠HBD则∠CBD = 90°折叠前后的对应角相等2．如图所示，一张矩形纸片沿BC折叠，顶点A落在点A′处，再过点A′折叠使折痕DE∥BC，若AB=4，AC=3，则△ADE的面积是．沿BC折叠，顶点落在点A’处，根据对称的性质得到BC垂直平分AA’，即AF = 12AA’，又DE∥BC，得到△ABC ∽△ADE，再根据相似三角形的面积比等于相似比的平方即可求出三角形ADE的面积= 24对称轴垂直平分对应点的连线3．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，得折痕DG ，求AG 的长．由勾股定理可得BD = 5，由对称的性质得△ADG ≌ △A ’DG ，由A ’D = AD = 3，AG ’ = AG ，则A ’B = 5 – 3 = 2，在Rt △A ’BG 中根据勾股定理，列方程可以求出AG 的值根据对称的性质得到相等的对应边和对应角，再在直角三角形中根据勾股定理列方程求解即可4．把矩形纸片ABCD 沿BE 折叠，使得BA 边与BC 重合，然后再沿着BF 折叠，使得折痕BE 也与BC 边重合，展开后如图所示，则∠DFB 等于（ ）根据对称的性质得到∠ABE=∠CBE ，∠EBF=∠CBF ，据此即可求出∠FBC 的度数，又知道∠C=90°，根据三角形外角的定义即可求出∠DFB = 112.5°注意折叠前后角的对应关系5．如图，沿矩形ABCD 的对角线BD 折叠，点C 落在点E 的位置，已知BC=8cm ，AB=6cm ，求折叠后重合部分的面积． ∵点C 与点E 关于直线BD 对称，∴∠1 = ∠2 ∵AD ∥BC ，∴∠1 = ∠3∴∠2 = ∠3 ∴FB = FD设FD = x ，则FB = x ，FA = 8 – x在Rt △BAF 中，BA 2 + AF 2 = BF 2∴62 + (8 - x)2 = x 2 解得x = 254所以，阴影部分的面积S △FBD = 12 FD ×AB = 12 ×254 ×6 = 754cm2重合部分是以折痕为底边的等腰三角形6．将一张矩形纸条ABCD 按如图所示折叠，若折叠角∠FEC=64°，则∠1= 度；△EFG 的形状 三角形．∵四边形CDFE 与四边形C ’D ’FE 关于直线EF 对称∴∠2 = ∠3 = 64°∴∠4 = 180° - 2 × 64° = 52° ∵AD ∥BC321F E D C B A54132G D‘FC‘DAGA'CA B D∴∠1 = ∠4 = 52°∠2 = ∠5又∵∠2 = ∠3∴∠3 = ∠5∴GE = GF∴△EFG是等腰三角形对折前后图形的位置变化，但形状、大小不变，注意一般情况下要画出对折前后的图形，便于寻找对折前后图形之间的关系，注意以折痕为底边的等腰△GEF7．如图，将矩形纸片ABCD按如下的顺序进行折叠：对折，展平，得折痕EF（如图①）；延CG折叠，使点B落在EF上的点B′处，（如图②）；展平，得折痕GC（如图③）；沿GH折叠，使点C落在DH上的点C′处，（如图④）；沿GC′折叠（如图⑤）；展平，得折痕GC′，GH（如图⑥）．（1）求图②中∠BCB′的大小；（2）图⑥中的△GCC′是正三角形吗？请说明理由．（1）由对称的性质可知：B’C=BC，然后在Rt△B′FC中，求得cos∠B’CF= 12，利用特殊角的三角函数值的知识即可求得∠BCB’= 60°；（2）首先根据题意得：GC平分∠BCB’，即可求得∠GCC’= 60°，然后由对称的性质知：GH是线段CC’的对称轴，可得GC’= GC，即可得△GCC’是正三角形．理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为四边形BCFE与四边形B′C′FE关于直线EF对称，则①②③④这四个三角形的周长之和等于正方形ABCD的周长折叠前后对应边相等9．如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，求四边形BCFE的面积设AE = x，则BE = GE = 4 - x，在Rt△AEG中，根据勾股定理有：AE2 + AG2 = GE2即：x2 + 4 = (4 - x)2解得x = 1.5，BE = EG = 4 – 1.5 = 2.5∵∠1 + ∠2 = 90°，∠2 + ∠3 = 90°∴∠1 = ∠3又∵∠A = ∠D = 90°∴△AEG ∽△DGP∴AEDG=EGGP，则1.52=2.5GP，解得GP =103PH = GH – GP = 4 - 103=23∵∠3 = ∠4，tan∠3 = tan∠1 = 3 4∴tan∠4 = 34，FHPH=34，FH =34×PH =34×23=12∴CF = FH = 1 2∴S梯形BCFE = 12(12+52)×4 = 6注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等10．如图，将一个边长为1的正方形纸片ABCD折叠，使点B落在边AD上不与A、D 重合．MN为折痕，折叠后B’C’与DN交于P．(1)连接BB’，那么BB’与MN的长度相等吗？为什么？(2)设BM=y，AB’=x，求y与x的函数关系式；(3)猜想当B点落在什么位置上时，折叠起来的梯形MNC’B’面积最小？并验证你的猜想．(1)BB’ = MN过点N作NH∥BC交AB于点H），证△ABB’≌△HNM(2)MB’ = MB = y，AM = 1 – y，AB’ = x在Rt△ABB’中BB’ = AB2 + AB'2= 1 + x2因为点B与点B’关于MN对称，所以BQ = B’Q，则BQ = 12 1 + x2由△BMQ∽△BB’A得BM×BA = BQ×BB’PC'NB CA DMB'QPHC'NB CA DMB'∴y = 12 1 + x2× 1 + x2=12(1 + x2)(3) 梯形MNC′B′的面积与梯形MNCB的面积相等由(1)可知，HM = AB’ = x，BH = BM – HM = y – x，则CN = y - x∴梯形MNCB的面积为：12(y – x + y) ×1 = 12(2y - x)= 12(2×12(1 + x2) – x)= 12(x -12)2 +38当x = 12时，即B点落在AD的中点时，梯形MNC’B’的面积有最小值，且最小值是38二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）∵∠α= ∠1，∠2 = ∠1∴∠α= ∠2∴2∠α+∠ABE=180°，即2∠α+30°=180°，解得∠α=75°．题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为作CD⊥AB，∵CE∥AB，∴∠1=∠2，根据翻折不变性，∠1=∠BCA，故∠2=∠BCA．∴AB=AC．又∵∠CAB=45°，∴在Rt△ADC中，AC = 2 2 ，AB = 2 2S△ＡＢＣ＝12AB×CD = 2 2a2130°BEFACD在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm 的长方形纸条成如图所示的形状，那么折痕PQ 的长是如图，作QH ⊥PA ，垂足为H ，则QH=2cm ， 由平行线的性质，得∠DPA=∠PAQ=60° 由折叠的性质，得∠DPA =∠PAQ ， ∴∠APQ=60°，又∵∠PAQ=∠APQ=60°， ∴△APQ 为等边三角形， 在Rt △PQH 中，sin ∠HPQ = HQPQ∴32 = 2PQ ，则PQ = 433注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ14．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（ ）图c 图b图aCDGFEC GDFEFBCAEBB∵AD ∥BC ，∴∠DEF=∠EFB=20°，在图b 中，GE = GF ，∠GFC=180°-2∠EFG=140°， 在图c 中∠CFE=∠GFC-∠EFG=120°，本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b ∠GFC=140°，图c 中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm 的长方形纸片ABCD ，沿对称轴EF 折叠成如图的形状，若折叠后，AB 与CD 间的距离为60cm ，则原纸片的宽AB 是（ ）设AB=xcm ．右图中，AF = CE = 35，EF = x根据轴对称图形的性质，得AE=CF=35-x （cm ）． 则有2（35-x ）+x=60， x=10．16．一根30cm 、宽3cm 的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P 的长度相等，则最初折叠时，求MA 的长将折叠这条展开如图，根据折叠的性质可知，两个梯形的上底等于纸条宽，即3cm ， 下底等于纸条宽的2倍，即6cm ， 两个三角形都为等腰直角三角形， 斜边为纸条宽的2倍，即6cm ，故超出点P 的长度为（30-15）÷2=7.5， AM=7.5+6=13.5GEFD AE FD B C A B C 60cm三、三角形中的折叠17．如图，把Rt △ABC （∠C=90°），使A ，B 两点重合，得到折痕ED ，再沿BE 折叠，C 点恰好与D 点重合，则CE ：AE=18．在△ABC 中，已知AB=2a ，∠A=30°，CD 是AB 边的中线，若将△ABC 沿CD 对折起来，折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14 ．（1）当中线CD 等于a 时，重叠部分的面积等于 ；（2）有如下结论（不在“CD 等于a ”的限制条件下）：①AC 边的长可以等于a ；②折叠前的△ABC 的面积可以等于32a 2；③折叠后，以A 、B 为端点的线段AB 与中线CD 平行且相等．其中， 结论正确（把你认为正确结论的代号都填上，若认为都不正确填“无”）． (1)∵CD = 12 AB∴∠ACB = 90°∵AB = 2a ，BC = a ，∴AC = 3a ∴S △ABC = 12 ×AC ×BC = 32a 2∴重叠部分的面积为：14×32a 2 = 38a 2(2)若AC = a ，如右图∵AD = a ，∴∠2 = 180°- 30°2 = 75°∠BDC = 180°- 75°= 105° ∴∠B'DC = 105°∴∠3 = 105°- 75°= 30° ∴∠1 = ∠3 ∴AC ∥B'D∴四边形AB'DC 是平行四边形∴重叠部分△CDE 的面积等于△ＡＢＣ的面积的14若折叠前△ABC 的面积等于32a 2 过点C 作CH ⊥AB 于点H ，则 12 ×AB ×CH = 32a 2 B'CDAB231EB'CDBACH =32a 又tan ∠1 =CH AH∴AH = 32a∴BH = 12a则tan ∠B =CHBH，得∠B = 60° ∴△CBD 是等边三角形 ∴∠2 = ∠4∴∠3 = ∠4，AD ∥CB 2又CB 2 = BC = BD = a ，∴CB 2 = AD ∴四边形ADCB 2是平行四边形则重叠部分△CDE 的面积是△ABC 面积的14(3)如右图，由对称的性质得，∠3 = ∠4，DA = DB 3 ∴∠1 = ∠2又∵∠3 + ∠4 = ∠1 +∠2 ∴∠4 = ∠1 ∴AB 3∥CD注意“角平分线+等腰三角形”的基本构图，折叠前后图形之间的对比，找出相等的对应角和对应边19．在△ABC 中，已知∠A=80°，∠C=30°，现把△CDE 沿DE 进行不同的折叠得△C ′DE ，对折叠后产生的夹角进行探究：（1）如图（1）把△CDE 沿DE 折叠在四边形ADEB 内，则求∠1+∠2的和； （2）如图（2）把△CDE 沿DE 折叠覆盖∠A ，则求∠1+∠2的和；（3）如图（3）把△CDE 沿DE 斜向上折叠，探求∠1、∠2、∠C 的关系．（1）根据折叠前后的图象全等可知，∠1=180°-2∠CDE ，∠2=180°-2∠CED ，再根据三角形内角和定理比可求出答案；（2）连接DG ，将∠ADG+∠AGD 作为一个整体，根据三角形内角和定理来求；3241EHB 2DABC3412B 3DA BC在第一次折叠中可得到∠EAD = ∠FAD在第二次折叠中可得到EF是AD的垂直平分线，则AD⊥EF∴∠AEF = ∠AFE∴△AEF是等腰三角形(1)由折叠可知∠AEB = ∠FEB，∠DEG = ∠BEG而∠BEG = 45°+ ∠α因为∠AEB + ∠BEG + ∠DEG = 180°所以 45°+ 2（45°+∠α）= 180°∠α = 22.5°由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

几何折叠问题解题技巧
1. 嘿，你知道吗？遇到几何折叠问题不要慌！比如把一张纸对折，这就是最常见的折叠呀！你得先找准折叠线，这就像是找到了解题的钥匙。

就像打开神秘宝盒一样，找到了关键就能轻松很多啦！
2. 喂，折叠后图形会有很多新产生的条件呢！比如说角度、边长啥的。

就好像变魔术一样，突然就多了好多线索。

像那个正方形纸一折叠，边长不就变了嘛，抓住这些变化很重要哦！
3. 哎呀呀，要善于利用对称关系呀！这可太关键了。

好比照镜子，镜子两边是对称的呀。

比如一个三角形折叠后，对称的边和角就能帮我们找到答案呢！
4. 嘿，注意观察折叠前后的不变量啊！这可是解题的法宝呢。

就如同你最爱的玩具一直都在那里一样，是不变的。

像那个长方形折叠，有些边的长度始终是那样哦。

5. 哇塞，遇到难题不要怕，要学会多角度思考呀！就像从不同方向看一个物体，会有不同的发现。

比如那个菱形折叠，从不同角度去分析，答案可能就出来啦！
6. 嘿，解题的时候要有耐心哦！不能着急忙慌的。

就好像搭积木，要一块一块慢慢来。

碰到复杂的折叠问题，沉住气慢慢找线索呀！
7. 哈哈，折叠问题里也藏着好多巧妙的地方呢！像隐藏的宝藏一样等你发现。

比如那个梯形的折叠，说不定藏着你想不到的惊喜哦！
8. 哟呵，要记住常用的解题方法呀！这可是你的秘密武器。

好比战士的宝剑。

像那种通过设未知数来解折叠问题，多好用呀！
9. 总之，几何折叠问题不难啦！只要掌握了这些技巧，就像掌握了魔法一样，什么难题都能轻松搞定！。

几何图形折叠问题【疑难点拨】1.折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2.折叠(翻折)意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图)，从而构造相似三角形，利用相似三角形求边或者角的度数．4.凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1..（2018•四川凉州•3分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（）AD=BC′B．∠EBD=∠EDB C．△ABE∽△CBD D．sin∠ABE=A．2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交于点D，点F是上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A．36π-108 B．108-32π C．2πD．π3. （2017浙江衢州）如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD 于点F，则DF的长等于（）A．B．C．D．4.（2018·山东青岛·3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=，则BC的长是（）A．B．32C．3 D．335.（2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4且∠AFG=60°，GE=2BG，则折痕EF的长为（）A．1 B．C．2 D．二、填空题：6.（2018·辽宁省盘锦市）如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC.AB 上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为．7.（2018·山东威海·8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C 与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=+1，则BC的长．8.（2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB= ．三、解答与计算题：9.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．10.（2018•山东枣庄•10分）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2，求BE的长．【能力篇】一、选择题：11.（2018·辽宁省阜新市）如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A1处，BC=8，那么线段AE的长度为( )．A．4 B．5 C．6 D．712.（2018·四川省攀枝花·3分）如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（）A．1 B．2 C．3 D．413.（2018·湖北省武汉·3分）如图，在⊙O中，点C在优弧上，将弧沿BC折叠后刚好经过AB的中点D．若⊙O的半径为，AB=4，则BC的长是（）A． B．C．D．二、填空题：14. (2018·辽宁省葫芦岛市) 如图，在矩形ABCD中，点E是CD的中点，将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部，将BF延长交AD于点G．若=，则= ．15.（2018·四川宜宾·3分）如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE 折叠，使点B落在矩形内点F处，下列结论正确的是（写出所有正确结论的序号）①当E为线段AB中点时，AF∥CE；②当E为线段AB中点时，AF=95；③当A、F、C三点共线时，AE=；④当A、F、C三点共线时，△CEF≌△AEF．三、解答与计算题：16.（2018·湖北省宜昌·11分）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B 的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；（2）如图2，①求证：BP=BF；②当AD=25，且AE＜DE时，求cos∠PCB的值；③当BP=9时，求BE•EF的值．17.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．18.（2018•江苏盐城•10分）如图，在以线段为直径的上取一点，连接、.将沿翻折后得到.（1）试说明点在上；（2）在线段的延长线上取一点，使.求证：为的切线；（3）在（2）的条件下，分别延长线段、相交于点，若，，求线段的长.【探究篇】19.（2018年江苏省泰州市•12分）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）（1）根据以上操作和发现，求的值；（2）将该矩形纸片展开．①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开．求证：∠HPC=90°；②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法．（不需说明理由）20.（2018年江苏省宿迁）如图，在边长为1的正方形ABCD中，动点E、F分别在边AB、CD上，将正方形ABCD 沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A、D重合），点C落在点N处，MN与CD交于点P，设BE=x，（1）当AM= 时，求x的值；（2）随着点M在边AD上位置的变化，△PDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；（3）设四边形BEFC的面积为S，求S与x之间的函数表达式，并求出S的最小值.几何图形折叠问题【疑难点拨】1.折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2.折叠(翻折)意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图)，从而构造相似三角形，利用相似三角形求边或者角的度数．4.凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1..（2018•四川凉州•3分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（）A．AD=BC′B．∠EBD=∠EDB C．△ABE∽△CBD D．sin∠ABE=【分析】主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案．【解答】解：A、BC=BC′，AD=BC，∴AD=BC′，所以正确．B、∠CBD=∠EDB，∠CBD=∠EBD，∴∠EBD=∠EDB正确．D、∵sin∠ABE=，∴∠EBD=∠EDB∴BE=DE∴sin∠ABE=．故选：C．【点评】本题主要用排除法，证明A，B，D都正确，所以不正确的就是C，排除法也是数学中一种常用的解题方法．2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交于点D，点F是上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A．36π-108 B．108-32π C．2πD．π【考点】MO：扇形面积的计算；P9：剪纸问题．【分析】先求出∠ODC=∠BOD=30°，作DE⊥OB可得DE=OD=3，先根据S弓形BD=S扇形BOD﹣S△BOD求得弓形的面积，再利用折叠的性质求得所有阴影部分面积．【解答】解：如图，∵CD⊥OA，∴∠DCO=∠AOB=90°，∵OA=OD=OB=6，OC=OA=OD，∴∠ODC=∠BOD=30°，作DE⊥OB于点E，则DE=OD=3，∴S弓形BD=S扇形BOD﹣S△BOD=﹣×6×3=3π﹣9，则剪下的纸片面积之和为12×（3π﹣9）=36π﹣108，故答案为：36π﹣108．故选A3. （2017浙江衢州）如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD 于点F，则DF的长等于（）A．B．C．D．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】根据折叠的性质得到AE=AB，∠E=∠B=90°，易证Rt△AEF≌Rt△CDF，即可得到结论EF=DF；易得FC=FA，设FA=x，则FC=x，FD=6﹣x，在Rt△CDF中利用勾股定理得到关于x的方程x2=42+（6﹣x）2，解方程求出x．【解答】解：∵矩形ABCD沿对角线AC对折，使△ABC落在△ACE的位置，∴AE=AB，∠E=∠B=90°，又∵四边形ABCD为矩形，∴AB=CD，∴AE=DC，而∠AFE=∠DFC，∵在△AEF与△CDF中，，∴△AEF≌△CDF（AAS），∴EF=DF；∵四边形ABCD为矩形，∴AD=BC=6，CD=AB=4，∵Rt△AEF≌Rt△CDF，∴FC=FA，设FA=x，则FC=x，FD=6﹣x，在Rt△CDF中，CF2=CD2+DF2，即x2=42+（6﹣x）2，解得x=，则FD=6﹣x=．故选：B．4.（2018·山东青岛·3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=，则BC的长是（）A．B．32C．3 D．33【分析】由折叠的性质可知∠B=∠EAF=45°，所以可求出∠AFB=90°，再直角三角形的性质可知EF=AB，所以AB=AC的长可求，再利用勾股定理即可求出BC的长．【解答】解：∵沿过点E的直线折叠，使点B与点A重合，∴∠B=∠EAF=45°，∴∠AFB=90°，∵点E为AB中点，∴EF=12AB，EF=32，∴AB=AC=3，∵∠BAC=90°，∴BC=2，故选：B．【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出∠AFB=90°是解题的关键．5.（2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4且∠AFG=60°，GE=2BG，则折痕EF的长为（）A．1 B．C．2 D．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】由折叠的性质可知，DF=GF、HE=CE、GH=DC、∠DFE=∠GFE，结合∠AFG=60°即可得出∠GFE=60°，进而可得出△GEF为等边三角形，在Rt△GHE中，通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC= EC，再由GE=2BG结合矩形面积为4，即可求出EC的长度，根据EF=GE=2EC即可求出结论．【解答】解：由折叠的性质可知，DF=GF，HE=CE，GH=DC，∠DFE=∠GFE．∵∠GFE+∠DFE=180°﹣∠AFG=120°，∴∠GFE=60°．∵AF∥GE，∠AFG=60°，∴∠FGE=∠AFG=60°，∴△GEF为等边三角形，∴EF=GE．∵∠FGE=60°，∠FGE+∠HGE=90°，∴∠HGE=30°．在Rt△GHE中，∠HGE=30°，∴GE=2HE=CE，∴GH==HE=CE．∵GE=2BG，∴BC=BG+GE+EC=4EC．∵矩形ABCD的面积为4，∴4EC•EC=4，∴EC=1，EF=GE=2．故选C．二、填空题：6.（2018·辽宁省盘锦市）如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC.AB 上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为．【解答】解：分两种情况：①如图，当∠CDM=90°时，△CDM是直角三角形，∵在Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，∴∠C=30°，AB=AC=，由折叠可得：∠MDN=∠A=60°，∴∠BDN=30°，∴BN=DN=AN，∴BN=AB=，∴AN=2BN=．∵∠DNB=60°，∴∠ANM=∠DNM=60°，∴∠AMN=60°，∴AN=MN=；②如图，当∠CMD=90°时，△CDM是直角三角形，由题可得：∠CDM=60°，∠A=∠MDN=60°，∴∠BDN=60°，∠BND=30°，∴BD=DN=AN，BN=BD\1AB=，∴AN=2，BN=，过N作NH⊥AM于H，则∠ANH=30°，∴AH=AN=1，HN=，由折叠可得：∠AMN=∠DMN=45°，∴△MNH是等腰直角三角形，∴HM=HN=，∴MN=．故答案为：或．7.（2018·山东威海·8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C 与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=+1，求BC的长．【分析】由题意知∠3=180°﹣2∠1=45°、∠4=180°﹣2∠2=30°、BE=KE、KF=FC，作KM⊥BC，设KM=x，知EM=x、MF=x，根据EF的长求得x=1，再进一步求解可得．【解答】解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K作KM⊥BC于点M，设KM=x，则EM=x、MF=x，∴x+x=+1，解得：x=1，∴EK=、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3++，∴BC的长为3++．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．8.（2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB= 75°．【分析】由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，从而可证明∠EBG=∠EGB．，然后再根据∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH，由平行线的性质可知∠AGB=∠GBC，从而易证∠AGB=∠BGH，据此可得答案．【解答】解：由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，∴∠EBG=∠EGB．∴∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH．又∵AD∥BC，∴∠AGB=∠GBC．∴∠AGB=∠BGH．∵∠DGH=30°，∴∠AGH=150°，∴∠AGB=∠AGH=75°，故答案为：75°．【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．三、解答与计算题：9.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE ≌△CED（SSS）；（2）根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出EF=DF，由此即可证出△DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ADE和△CED中，，∴△ADE≌△CED（SSS）．（2）由（1）得△ADE≌△CED，∴∠DEA=∠EDC，即∠DEF=∠EDF，∴EF=DF，∴△DEF是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出AD=CE、AE=CD；（2）利用全等三角形的性质找出∠DEF=∠EDF．10.（2018•山东枣庄•10分）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2，求BE的长．【分析】（1）先依据翻折的性质和平行线的性质证明∠DGF=∠DFG，从而得到GD=DF，接下来依据翻折的性质可证明DG=GE=DF=EF；（2）连接DE，交AF于点O．由菱形的性质可知GF⊥DE，OG=OF=GF，接下来，证明△DOF∽△ADF，由相似三角形的性质可证明DF2=FO•AF，于是可得到GE、AF、FG的数量关系；（3）过点G作GH⊥DC，垂足为H．利用（2）的结论可求得FG=4，然后再△ADF中依据勾股定理可求得AD的长，然后再证明△FGH∽△FAD，利用相似三角形的性质可求得GH的长，最后依据BE=AD﹣GH求解即可．【解答】解：（1）证明：∵GE∥DF，∴∠EGF=∠DFG．∵由翻折的性质可知：GD=GE，DF=EF，∠DGF=∠EGF，∴∠DGF=∠DFG．∴GD=DF．∴DG=GE=DF=EF．∴四边形EFDG为菱形．（2）EG2=GF•AF．理由：如图1所示：连接DE，交AF于点O．∵四边形EFDG为菱形，∴GF⊥DE，OG=OF=GF．∵∠DOF=∠ADF=90°，∠OFD=∠DFA，∴△DOF∽△ADF．∴，即DF2=FO•AF．∵FO=GF，DF=EG，∴EG2=GF•AF．（3）如图2所示：过点G作GH⊥DC，垂足为H．∵EG2=GF•AF，AG=6，EG=2，∴20=FG（FG+6），整理得：FG2+6FG﹣40=0．解得：FG=4，FG=﹣10（舍去）．∵DF=GE=2，AF=10，∴AD==4．∵GH⊥DC，AD⊥DC，∴GH∥AD．∴△FGH∽△FAD．∴，即=．∴GH=．∴BE=AD﹣GH=4﹣=．【点评】本题主要考查的是四边形与三角形的综合应用，解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用，利用相似三角形的性质得到DF2=FO•AF是解题答问题（2）的关键，依据相似三角形的性质求得GH的长是解答问题（3）的关键．【能力篇】一、选择题：11.（2018·辽宁省阜新市）如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A1处，BC=8，那么线段AE的长度为( )．A．4 B．5 C．6 D．7【解答】解：由折叠的性质可得AE=A1E．∵△ABC为等腰直角三角形，BC=8，∴AB=8．∵A1为BC的中点，∴A1B=4，设AE=A1E=x，则BE=8﹣x．在Rt△A1BE中，由勾股定理可得42+（8﹣x）2=x2，解得x=5．故答案为：5．故选B12.（2018·四川省攀枝花·3分）如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（）A．1 B．2 C．3 D．4解：①如图，EC，BP交于点G；∵点P是点B关于直线EC的对称点，∴EC垂直平分BP，∴EP=EB，∴∠EBP=∠EPB．∵点E为AB中点，∴AE=EB，∴AE=EP，∴∠PAB=∠PBA．∵∠PAB+∠PBA+∠APB=180°，即∠PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，∴∠PAB+∠PBA=90°，∴AP⊥BP，∴AF∥EC；∵AE∥CF，∴四边形AECF是平行四边形，故①正确；②∵∠APB=90°，∴∠APQ+∠BPC=90°，由折叠得：BC=PC，∴∠BPC=∠PBC．∵四边形ABCD是正方形，∴∠ABC=∠ABP+∠PBC=90°，∴∠ABP=∠APQ，故②正确；③∵AF∥EC，∴∠FPC=∠PCE=∠BCE．∵∠PFC是钝角，当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，如右图，△PCF不一定是等腰三角形，故③不正确；④∵AF=EC，AD=BC=PC，∠ADF=∠EPC=90°，∴Rt△EPC≌△FDA（HL）．∵∠ADF=∠APB=90°，∠FAD=∠ABP，当BP=AD或△BPC是等边三角形时，△APB≌△FDA，∴△APB≌△EPC，故④不正确；其中正确结论有①②，2个．故选B．13. （2018·湖北省武汉·3分）如图，在⊙O 中，点C 在优弧上，将弧沿BC 折叠后刚好经过AB 的中点D ．若⊙O 的半径为，AB=4，则BC 的长是（ ）A ．B ．C ．D ．【分析】连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图，利用垂径定理得到OD ⊥AB ，则AD=BD=AB=2，于是根据勾股定理可计算出OD=1，再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆，则根据圆周角定理得到=，所以AC=DC ，利用等腰三角形的性质得AE=DE=1，接着证明四边形ODEF 为正方形得到OF=EF=1，然后计算出CF 后得到CE=BE=3，于是得到BC=3 2．【解答】解：连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图， ∵D 为AB 的中点， ∴OD ⊥AB ， ∴AD=BD=AB=2，在Rt △OBD 中，OD=22(5)2 =1， ∵将弧沿BC 折叠后刚好经过AB 的中点D ．∴弧AC 和弧CD 所在的圆为等圆， ∴=，∴AC=DC ， ∴AE=DE=1，易得四边形ODEF 为正方形， ∴OF=EF=1，在Rt △OCF 中，CF=22(5)1 ， ∴CE=CF+EF=2+1=3， 而BE=BD+DE=2+1=3， ∴BC=3．故选：B ．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理和垂径定理． 二、填空题：14. (2018·辽宁省葫芦岛市) 如图，在矩形ABCD 中，点E 是CD 的中点，将△BCE 沿BE 折叠后得到△BEF 、且点F 在矩形ABCD 的内部，将BF 延长交AD 于点G ．若=，则= ．【解答】解：连接GE ．∵点E 是CD 的中点，∴EC=DE ．∵将△BCE 沿BE 折叠后得到△BEF 、且点F 在矩形ABCD 的内部，∴EF=DE ，∠BFE=90°．在Rt △EDG 和Rt △EFG 中，∴Rt △EDG ≌Rt △EFG （HL ），∴FG=DG ．∵=，∴设DG=FG=a，则AG=7a，故AD=BC=8a，则BG=BF+FG=9a，∴AB==4a，故==．故答案为：．15.（2018·四川宜宾·3分）如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE 折叠，使点B落在矩形内点F处，下列结论正确的是①②③（写出所有正确结论的序号）①当E为线段AB中点时，AF∥CE；②当E为线段AB中点时，AF=95；③当A、F、C三点共线时，AE=；④当A、F、C三点共线时，△CEF≌△AEF．【考点】PB：翻折变换（折叠问题）；KB：全等三角形的判定；LB：矩形的性质．【分析】分两种情形分别求解即可解决问题；【解答】解：如图1中，当AE=EB时，∵AE=EB=EF，∴∠EAF=∠EFA，∵∠CEF=∠CEB，∠BEF=∠EAF+∠EFA，∴∠BEC=∠EAF，∴AF∥EC，故①正确，作EM⊥AF，则AM=FM，在Rt△ECB中，EC==，，∵∠AME=∠B=90°，∠EAM=∠CEB，∴△CEB∽△EAM，∴=，∴=，∴AM=，∴AF=2AM=95，故②正确，如图2中，当A、F、C共线时，设AE=x．则EB=EF=3﹣x，AF=13﹣2，在Rt△AEF中，∵AE2=AF2+EF2，∴x2=（﹣2）2+（3﹣x）2，∴x=，，∴AE=，故③正确，如果，△CEF≌△AEF，则∠EAF=∠ECF=∠ECB=30°，显然不符合题意，故④错误，故答案为①②③．【点评】本题考查翻折变换、全等三角形的性质、勾股定理、矩形的性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考填空题中的压轴题．三、解答与计算题：16.（2018·湖北省宜昌·11分）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B 的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；（2）如图2，①求证：BP=BF；②当AD=25，且AE＜DE时，求cos∠PCB的值；③当BP=9时，求BE•EF的值．【分析】（1）先判断出∠A=∠D=90°，AB=DC再判断出AE=DE，即可得出结论；（2）①利用折叠的性质，得出∠PGC=∠PBC=90°，∠BPC=∠GPC，进而判断出∠GPF=∠PFB即可得出结论；②判断出△ABE∽△DEC，得出比例式建立方程求解即可得出AE=9，DE=16，再判断出△ECF∽△GCP，进而求出PC，即可得出结论；③判断出△GEF∽△EAB，即可得出结论．【解答】解：（1）在矩形ABCD中，∠A=∠D=90°，AB=DC，∵E是AD中点，∴AE=DE，在△ABE和△DCE中，，∴△ABE≌△DCE（SAS）；（2）①在矩形ABCD，∠ABC=90°，∵△BPC沿PC折叠得到△GPC，∴∠PGC=∠PBC=90°，∠BPC=∠GPC，∵BE⊥CG，∴BE∥PG，∴∠GPF=∠PFB，∴∠BPF=∠BFP，∴BP=BF；②当AD=25时，∵∠BEC=90°，∴∠AEB+∠CED=90°，∵∠AEB+∠ABE=90°，∴∠CED=∠ABE，∵∠A=∠D=90°，∴△ABE∽△DEC，∴，设AE=x，∴DE=25﹣x，∴，∴x=9或x=16，∵AE＜DE，∴AE=9，DE=16，∴CE=20，BE=15，由折叠得，BP=PG，∴BP=BF=PG，∵BE∥PG，∴△ECF∽△GCP，∴，设BP=BF=PG=y，∴，∴y=，∴BP=，在Rt△PBC中，PC=，cos∠PCB==；③如图，连接FG，∵∠GEF=∠BAE=90°，∵BF∥PG，BF=PG，∴▱BPGF是菱形，∴BP∥GF，∴∠GFE=∠ABE，∴△GEF∽△EAB，∴，∴BE•EF=AB•GF=12×9=108．【点评】此题是四边形综合题，主要考查了矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，折叠的性质，利用方程的思想解决问题是解本题的关键．17.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE ≌△CED（SSS）；（2）根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出EF=DF，由此即可证出△DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ADE和△CED中，，∴△ADE≌△CED（SSS）．（2）由（1）得△ADE≌△CED，∴∠DEA=∠EDC，即∠DEF=∠EDF，∴EF=DF，∴△DEF是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出AD=CE、AE=CD；（2）利用全等三角形的性质找出∠DEF=∠EDF．18.（2018•江苏盐城•10分）如图，在以线段为直径的上取一点，连接、.将沿翻折后得到.（1）试说明点在上；（2）在线段的延长线上取一点，使.求证：为的切线；（3）在（2）的条件下，分别延长线段、相交于点，若，，求线段的长. 【答案】（1）解：连接OC，OD，由翻折可得OD=OC，∵OC是⊙O的半径，∴点D在⊙O上。

1 / 2几何图形折叠问题解法浅析贵州省兴仁县巴铃中学 张志明折叠型问题是近年中考的热点问题，通常是把某个图形按照给定的条件折叠，通过折叠前后图形变换的相互关系来命题。

折叠型问题立意新颖，变幻巧妙，对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。

下面我们一起来探究这种题型的解法。

折叠的规律是:折叠部分的图形，折叠前后，关于折痕成轴对称，两图形全等。

1. 如图，长方形ABCD 沿AE 折叠，使D 落在边BC 上的F 点处，如果∠BAF=60°，则 ∠DAE=___。

答案：A ，15°分析 根据折叠的规律：可证△ADE ≌△AFE,从而∠DAE=∠FAE=(90°-60°)÷2=150A.15°B.30°C.45°D.60°2. 如图，折叠矩形纸片ABCD ，先折出折痕（对角线）BD ，再折叠，使AD 落在对角线BD 上，得折痕DG ，若AB = 2，BC = 1，求AG. 答案：AG =215- 分析 折叠后的图形（如图一），设A 点落在BD 上的位置为A 1，则 A 点关于直线 DG 的对称点为点 A 1， 连结 A 1G ，（如图二）可知△ADG ≌ △A 1DG ，AG = A 1G ， AD = A 1D 。

∵矩形ABCD ，AB = 2，BC = 1，∴BD =2212+=5，BA 1 =5–1，∵∠ BA 1G = ∠ A = 90°。

设AG = A 1G= X ，在Rt △BA 1G 中，利用勾股定理列出方程：x 2 +(5–1)2 = ( 2 – x )2,∴ x =215-，即：AG =215-. 3. 如图，在Rt △ABC 中，∠ACB=90°∠A<∠B ，CM 是斜边AB 的中线，将△ACM 沿直线CM折叠，点A 落在D 处，如果CD 恰好与AB 垂直，那么∠A 等于_____.答案：30°解析：根据折叠规律：可知△CMA ≌ △CMD ，∴ ∠ 1 = ∠ 2，∵CM 为斜边AB 的中线，∴ CM = AM ，∴ ∠ A= ∠ 1。

空间几何中的折叠问题例题和知识点总结在空间几何的学习中，折叠问题是一个重要且具有一定难度的考点。

通过折叠，可以将平面图形转化为空间图形，从而增加了问题的复杂性和抽象性。

下面，我们将通过一些例题来深入探讨空间几何中的折叠问题，并对相关知识点进行总结。

一、折叠问题的基本概念折叠问题通常是指将一个平面图形沿着某条直线或折线进行折叠，使其成为一个空间几何体。

在这个过程中，图形的某些元素（如线段的长度、角度的大小等）保持不变，而有些元素则会发生变化。

例如，将一个矩形沿着其中一条边折叠，可以得到一个三棱柱；将一个直角三角形沿着斜边折叠，可以得到一个三棱锥。

二、折叠问题的关键知识点1、不变量在折叠过程中，有些量是不变的。

例如，折叠前后对应线段的长度不变，对应角度的大小不变。

2、垂直关系折叠前后，原来垂直的线段和平面在折叠后仍然垂直。

3、距离和角度的变化折叠后，某些线段之间的距离和角度会发生变化，需要根据折叠的方式和几何关系进行重新计算。

三、例题分析例 1：已知矩形 ABCD 中，AB ＝ 3，BC ＝ 4。

现将矩形沿着对角线 AC 折叠，求折叠后点 B 到平面 ACD 的距离。

解：首先，通过勾股定理求出 AC 的长度：AC ＝√（AB²＋ BC²) ＝ 5设点 B 折叠后对应的点为 B'，由于折叠前后三角形 ABC 的面积不变。

三角形 ABC 的面积＝ 1/2 × AB × BC ＝ 1/2 × AC × h （h 为点 B 到平面 ACD 的距离）所以 h ＝（AB × BC) ／ AC ＝（3 × 4) ／ 5 ＝ 12 ／ 5例 2：如图，在直角三角形 ABC 中，∠ACB ＝ 90°，AC ＝ 2，BC ＝ 1，将三角形 ABC 沿斜边 AB 折叠，得到三棱锥 C ABD。

求证：平面 CAD ⊥平面 BAD。

初中数学几何图形中的折叠问题解题思路折叠问题中的背景图形通常有，三角形、正方形、矩形、梯形等，解决这类问题的关键是一定要灵活运用轴对称和背景图形的性质。

轴对称性质：折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。

典型例题：例题1、如图，在 Rt△ABC 中，∠ACB=90°，AB=10，AC=8，E、F 分别为 AB、BC 上的点，沿线段 EF 将∠B 折叠，使点 B 恰好落在AC 上的点 D 处，试问当△ADE 恰好为直角三角形时，此时 BE 的长度为多少?解题思路：△ADE 为直角三角形分两种情况：①∠ADE = 90°，②∠AED = 90°，此题需要分类讨论，结合三角形的相似、折叠的性质，来求折叠中线段的长度，关键是能画出折叠后的图形。

解答过程：当∠ADE = 90°时，如下图所示：证明：先来证明四边形 DEBF 为棱形：∵在 Rt△ABC 中，∠ACB=90°，∠ADE = 90°，∴ DE∥BC ，∴∠DEF = ∠EFB ，又∵沿线段 EF 将∠B 折叠，∴ DE = BE ,DF = BF ，∠DFE = ∠BFE ，∴∠DEF = ∠DFE ，DE = DF = BF ，∴四边形 DEBF 为棱形。

(一组对边平行且相等的四边形是平行四边形，邻边相等的平行四边形是棱形)。

再来证明Rt△ADE ∽Rt△ACB (相似三角形判断图形中的“A”字型)∵在三角形 ACB 中，DE∥BC ，∴ Rt△ADE ∽ Rt△ACB ，设棱形 DEBF 的边长为 x , 则有 DE = x , AE = 10 - x ,在 Rt△ACB 中，AB = 10 , AC = 8 ,由勾股定理得：BC = 6 。

∴ DE : BC = AE : AB , 即 x : 6 = (10-x) : 10 ,解得 x = 15/4 ,∴ BE = 15/4 ;当∠AED = 90°时，如下图所示：易证 Rt△AED ∽ Rt△ACB ，由折叠的性质可得 DE = BE ，设 DE = BE = x ，则 AE = 10 - x ，由相似三角形的性质可得：DE : BC = AE : AC , 即 x : 6 = ( 10 -x ) : 8 ,解得 x = 30/7，∴ BE = 30/7 。

初中数学折叠问题模型折叠问题一直是初中数学中的热门话题，它既考验了学生的几何思维，又锻炼了他们的逻辑分析能力。

本文将从以下几个方面对初中数学折叠问题进行深入探讨，以期帮助同学们掌握这一问题的解决方法。

一、折叠问题的基本概念折叠问题是指在平面几何中，将一个平面图形沿着某一条线段折叠，使其两部分重合或变成一个整体的过程。

在初中数学阶段，折叠问题主要涉及到几何图形的折叠、计算和分析。

二、初中数学中常见的折叠问题类型1.图形折叠：将一个几何图形如正方形、长方形、三角形等沿着某一条线段折叠，求解折叠后的图形面积、周长等。

2.角度计算：在折叠过程中，涉及到角度的计算与证明。

如折叠前后的两个角度相等、互补或互余等。

3.线段长度计算：折叠前后的线段长度关系，如折叠后的线段长度是折叠前的一半、两倍等。

4.几何图形的组合与分解：通过折叠将几个简单的几何图形组合成一个复杂的图形，或反之，将一个复杂的图形分解成几个简单的几何图形。

三、解决折叠问题的方法与技巧1.熟练掌握几何图形的性质，如角度、边长、面积等关系。

2.画图辅助，直观地展示折叠过程，帮助分析问题。

3.运用方程、比例等数学方法求解未知量。

4.熟练运用折叠过程中的不变量，如折叠前后的角度和、周长等。

四、实际应用案例分析以一个正方形为例，将其沿对角线折叠，可以得到两个直角三角形。

根据折叠后的三角形，我们可以求解原正方形的边长、面积等参数。

五、总结与建议初中数学折叠问题不仅有助于提高同学们的空间想象能力，还能锻炼他们的逻辑思维。

要想解决这类问题，关键在于掌握几何图形的性质，灵活运用数学方法，以及画图辅助分析。

建议同学们多做练习，积累经验，逐步提高自己的解题能力。

第15讲 立体几何折叠问题1．如图，矩形ABCD 中，24AD AB ==，E 为BC 的中点，现将BAE ∆与DCE ∆折起，使得平面BAE 及平面DEC 都与平面ADE 垂直．（1）求证：//BC 平面ADE ； （2）求二面角A BE C --的余弦值．【解答】解：（1）证明：分别取AE ，DE 的中点M ，N ，连结BM ，CN ，MN ， 则BM AE ⊥，CN DE ⊥，平面BAE 与平面DEC 都与平面ADE 垂直， BM ∴⊥平面ADE ，CN ⊥平面ADE ，由线面垂直的性质定理得//BM CN ，BM CN =，∴四边形BCNM 是平行四边形，//BC MN ∴， BC ⊂/平面ADE ，//BC ∴平面ADE ．（2）解：如图，以E 为原点，ED ，EA 为x ，y 正半轴，过E 作平面ADE 的垂线为z 轴，建立空间直角坐标系，则B ，C ，平面ABE 的法向量(1n =，0，0)， 设平面CBE 的法向量(m x =，y ，)z ，则2020EB m y EC m x ⎧=+=⎪⎨==⎪⎩，取1x =，得(1m =，1，1)-， 设二面角A BE C --的平面角为θ，由图知θ为钝角，||1cos ||||3m n m n θ∴=-=-=∴二面角A BE C --的余弦值为．2．如图，在直角梯形ABCD 中，//AD BC ，AB BC ⊥，且24BC AD ==，E ，F 分别为线段AB ，DC 的中点，沿EF 把AEFD 折起，使AE CF ⊥，得到如下的立体图形． （1）证明：平面AEFD ⊥平面EBCF ；（2）若BD EC ⊥，求二面角F BD C --的余弦值．【解答】（1）证明：在直角梯形ABCD 中，//AD BC ，AB BC ⊥， E ，F 分别为线段AB ，DC 的中点， //EF AD ∴，AE EF ∴⊥，又AE CF ⊥，且EF CF F =，AE ∴⊥平面EBCF ， AE ⊂平面AEFD ，∴平面AEFD ⊥平面EBCF ．（2）解：由（1）可得EA ，EB ，EF 两两垂直， 故以E 为原点建立空间直角坐标系，（如图）设AE m =，则(0E ，0，0)，(0A ，0，)m ，(B m ，0，0)， (0F ，3，0)，(C m ，4，0)，(0D ，2，)m ，∴(BD m =-，2，)m ，(,4,0)EC m =，DB EC ⊥，280m ∴-+=，22m ∴=∴(22BD =-，2，2)，(22,3,0)FB =-，(0,4,0)CB =-，设面DBF 的法向量为(,,)m x y z =，则00m BD m FB ⎧⋅=⎪⎨⋅=⎪⎩，即2222202230x y z x y ⎧-++=⎪⎨-=⎪⎩，令4y =可得：(32m =，42)， 同理可得平面CDB 的法向量为(1,0,1)n =， 422cos ,||||362m n m n m n ⋅∴<>===⨯．由图形可知二面角F BD C --为锐角，∴二面角F BD C --的余弦值为23．3．如图1，在平行四边形11ABB A 中，160ABB ∠=︒，4AB =，12AA =，C 、1C 分别为AB 、11A B 的中点，现把平行四边形111ABB A 沿1CC 折起如图2所示，连接1B C 、1B A 、11B A ． （1）求证：11AB CC ⊥；（2）若16AB =11C AB A --的正弦值．【解答】证明：（1）取1CC 的中点O ，连接OA ，1OB ，1AC ，在平行四边形11ABB A 中，160ABB ∠=︒，4AB =，12AA =，C 、1C 分别为AB 、11A B 的中点， 1ACC ∴∆，1BCC ∆为正三角形，则1AO CC ⊥，11OB CC ⊥，又1AOOB O =，1CC ∴⊥平面1OAB ，1AB ⊂平面1OAB 11AB CC ∴⊥；4⋯分（2）160ABB ∠=︒，4AB =，12AA =，C 、1C 分别为AB 、11A B 的中点，2AC ∴=，13OA OB ==16AB =22211OA OB AB +=，则三角形1AOB 为直角三角形，则1AO OB ⊥，6⋯分以O 为原点，以OC ，1OB ，OA 为x ，y ，z 轴建立空间直角坐标系， 则(1C ，0，0)，1(0B ，30)，1(1C -，0，0)，(0A ，0，3)，则1(2,0,0)CC =- 则11(2,0,0)AA CC ==-，1(0AB =33)-，(1AC =，0，3)-， 设平面1AB C 的法向量为(,,)n x y z =，则133030n AB y z n AC x z ⎧==⎪⎨==⎪⎩，令1z =，则1y =，3x =(3,1,1)n =， 设平面11A B A 的法向量为(,,)m x y z =，则1120330m AA x m AB y z ⎧=-=⎪⎨==⎪⎩，令1z =，则0x =，1y =，即(0,1,1)m =，8⋯分则10cos ,105m n <>=分 ∴二面角11C AB A --15．12⋯分．4．如图1所示，在等腰梯形ABCD 中，,3,15,33BE AD BC AD BE ⊥===把ABE ∆沿BE 折起，使得62AC =得到四棱锥A BCDE -．如图2所示． （1）求证：面ACE ⊥面ABD ；（2）求平面ABE 与平面ACD 所成锐二面角的余弦值． 【解答】证明：（1）在等腰梯形ABCD 中3BC =，15AD =，BE AD ⊥，可知6AE =，9DE =．因为3,33,BC BE BE AD ==⊥，可得6CE =．又因为6,62AE AC ==，即222AC CE AE =+，则AE EC ⊥．又BE AE ⊥，BEEC E =，可得AE ⊥面BCDE ，故AE BD ⊥．又因为tan 333DE DBE BE ∠===， 则60DBE ∠=︒，3tan 33BC BEC BE ∠===，则30BEC ∠=︒， 所以CE BD ⊥，又AE EC E =，所以BD ⊥面ACE ，又BD ⊂面ABD ，所以面ABD ⊥面ACE ；解：（2）设ECBD O =，过点O 作//OF AE 交AC 于点F ，以点O 为原点，以OB ，OC ，OF 所在直线分别为x ，y ，z 轴，建立如图所示的空间直角坐标系O BCF -． 在BCE ∆中，30BEO ∠=︒，BO EO ⊥，∴9333,,22EO CO BO ===2339((0,,0),(0,,0)22B C E -，1//,,62FO AE FO AE AE ==，3FO ∴=，则9(0,0,3),(0,,6)2F A -，//DE BC ，9DE =，∴3ED BC =，∴93(D ，∴339933(,,0),(0,0,6),(0,6,6),(,0)2222BE AE CA CD ===-=--，设平面ABE 的法向量为1111(,,)n x y z =，由1111160339022n AE z n BE y ⎧==⎪⎨=+=⎪⎩，取13x =ABE 的法向量为1(3,1,0)n =-， 设平面ACD 的一个法向量为2222(,,)n x y z =，由222222660933022n CA y z n CD y ⎧=-+=⎪⎨=--=⎪⎩， 取21x =，可得平面ABE 的一个法向量为2(1n =，33-，33)-．设平面ABE 与平面ACD所成锐二面角为θ，则1212||432165cos ||||255n n n n θ===，所以平面ABE 与平面ACD 所成锐二面角的余弦值为21655．如图1，菱形ABCD 的边长为12，60BAD ∠=︒，AC 与BD 交于O 点．将菱形ABCD 沿对角线AC 折起，得到三棱锥B ACD -，点M 是棱BC 的中点，62DM = （Ⅰ）求证：平面ODM ⊥平面ABC ； （Ⅱ）求二面角M AD C --的余弦值．【解答】（本小题满分12分） 证明：（Ⅰ）ABCD 是菱形， AD DC ∴=，OD AC ⊥，ADC ∆中，12AD DC ==，120ADC ∠=︒， 6OD ∴=，又M 是BC 中点，∴16,622OM AB MD === 222OD OM MD +=，DO OM ∴⊥，OM ，AC ⊂面ABC ，OM AC O =，OD ∴⊥面ABC ，又OD ⊂平面ODM ，∴平面ODM ⊥平面ABC ．⋯（6分） 解：（Ⅱ）由题意，OD OC ⊥，OB OC ⊥，又由（Ⅰ）知OB OD ⊥，建立如图所示空间直角坐标系，由条件知：(6,0,0),(0,63,0),(0,33,3)D A M - 故(0,93,3),(6,63,0)AM AD ==， 设平面MAD 的法向量(,,)m x y z =，则00m AM m AD ⎧=⎪⎨=⎪⎩，即93306630y z x ⎧+=⎪⎨+=⎪⎩，令3y =-3x =，9z = ∴(3,3,9)m =-由条件知OB ⊥平面ACD ，故取平面ACD 的法向量为(0,0,1)n = 所以，393cos ,||||31m n m n m n 〈〉==由图知二面角M AD C --为锐二面角， 故二面角M AD C --393（12分）6．如图1，已知在菱形ABCD 中，120B ∠=︒，E 为AB 的中点，现将四边形EBCD 沿DE 折起至EBHD ，如图2．（1）求证：DE ⊥面ABE ；（2）若二面角A DE H --的大小为23π，求平面ABH 与平面ADE 所成锐二面角的余弦值． 【解答】（1）证明：四边形ABCD 为菱形，且120B ∠=︒， ABD ∴∆为正三角形， E 为AB 的中点，DE AE ∴⊥，DE BE ⊥， DE ∴⊥面ABE ；（2）解：以点E 为坐标原点，分别以线段ED ，EA 所在直线为x ，y 轴，再以过点E 且垂直于平面ADE 且向上的直线为z 轴，建立空间直角坐标系如图所示．DE ⊥面ABE ，AEB ∴∠为二面角A DE H --的一个平面角，则23AEB π∠=， 设1AE =，则(0E ，0，0)，(0A ，1，0)，(0B ，12-3)，(3D 0，0)，由2DH EB =，得(3,3)H -，∴33(0,2AB =-，(3,3)AH =-， 设平面ABH 的法向量为(,,)n x y z =，则33023230n AB y n AH x y z ⎧=-+=⎪⎨⎪=-=⎩，令3y =，得(1,3,3)n =-．而平面ADE 的一个法向量为(0,0,1)m =，设平面ABH 与平面ADE 所成锐二面角的大小为θ，则313313cos |||||||13n m n m θ===． ∴平面ABH 与平面ADE 313．7．如图1，四边形ABCD 中AC BD ⊥，2222CE AE BE DE ====，将四边形ABCD 沿着BD 折叠，得到图2所示的三棱锥A BCD -，其中AB CD ⊥． （Ⅰ）证明：平面ACD ⊥平面BAD ；（Ⅱ）若F 为CD 中点，求二面角C AB F --的余弦值．【解答】证明：（Ⅰ）AE BD ⊥，且BE DE =，ABD ∴∆是等腰直角三角形，AB AD ∴⊥，又AB CD ⊥，且AD ，CD ⊂平面ACD ，ADCD D =，AB ∴⊥平面ACD ，又AB ⊂平面BAD ，∴平面ACD ⊥平面BAD ． 解：（Ⅱ）以E 为原点，EC 为x 轴，ED 为y 轴，过E 作平面BDC 的垂直为z 轴，建立空间直角坐标系，过A 作平面BCD 的垂线，垂足为G ，根据对称性，G 点在x 轴上，设AG h =，由题设知： (0E ，0，0)，(2C ，0，0)，(0B ，1-，0)，(0D ，1，0)， 2(1A h -0，)h ，(1F ，12，0)，2(1BA h =-1，)h ，(2DC =，1-，0)，AB CD ⊥，∴22110BA DC h =-=，解得3h =，13(2A ∴． 13(2BA =，(1BF =，32，0)，设平面ABF 的法向量(a μ=，b ，)c ，则1302302BA a b BF a b μμ⎧=+=⎪⎪⎨⎪=+=⎪⎩， 令9a =，得(9μ=，6-，3)，AD AB ⊥，AD AC ⊥，2(1DA ∴=，2-3)是平面ABC 的一个法向量，cos μ∴<，(2)91231525|||2|1208DA DA DA μμ++>===，二面角C AB F --是锐角，∴二面角C AB F --的余弦15．8．如图1，在直角梯形ABCD 中，//AD BC ，AB BC ⊥，BD DC ⊥，点E 是BC 边的中点，将ABD ∆沿BD 折起，使平面ABD ⊥平面BCD ，连接AE ，AC ，DE ，得到如图2所示的几何体． （Ⅰ）求证：AB ⊥平面ADC ；（Ⅱ）若1AD =，二面角C AB D --6，求二面角B AD E --的余弦值．【解答】解：（Ⅰ）因为平面ABD ⊥平面BCD ，平面ABD ⋂平面BCD BD =，又BD DC ⊥，所以DC ⊥平面ABD ．⋯（1分）因为AB ⊂平面ABD ，所以DC AB ⊥．⋯（2分） 又因为折叠前后均有AD AB ⊥，DCAD D =，⋯（3分）所以AB ⊥平面ADC ．⋯（4分）（Ⅱ）由（Ⅰ）知AB ⊥平面ADC ，所以二面角C AB D --的平面角为CAD ∠．⋯（5分） 又DC ⊥平面ABD ，AD ⊂平面ABD ，所以DC AD ⊥．依题意tan 6CDCAD AD∠==．⋯（6分） 因为1AD =，所以6CD =(0)AB x x =>，则21BD x =+ 依题意~ABD BDC ∆∆，所以AB CDAD BD=，即2611x x =+⋯（7分）解得2x ，故222,3,3AB BD BC BD CD ===+．⋯（8分）如图所示，建立空间直角坐标系D xyz -，则(0D ，0，0)，(3,0,0)B ，6,0)C ，36(E ，36(A ，所以36(2DE =，36(3DA =．由（Ⅰ）知平面BAD 的法向量(0,1,0)n =．⋯（9分）设平面ADE 的法向量(,,)m x y z =由0,0m DE m DA ⋅=⋅=得360360.y == 令6x =，得3,3y z =-=，所以(6,3,3)m =-．⋯（10分）所以1cos ,||||2n m n m n m ⋅<>==-⋅．⋯（11分）由图可知二面角B AD E --的平面角为锐角，所以二面角B AD E --的余弦值为12．⋯（12分） 9．如图所示，在平行四边形ABCD 中，4AB =，BC =45ABC ∠=︒，点E 是CD 边的中点，将DAE ∆沿AEE 折起，使点D 到达点P 的位置，且PB =（1）求证：平面PAE ⊥平面ABCE ；（2）若平面PAE 和平面PBC 的交线为l ，求二面角B lE --的余弦值．【解答】（1）证明：连接BE ，在平行四边形ABCD 中，2DE =，AD =45ADC ∠=︒，2AE∴=AE DE ∴⊥，即AE PE ⊥，且AE BA ⊥．在Rt BEA ∆中，得BE ==．又2PE =，PB =222PE BE PB ∴+=，即PE BE ⊥．又AE ⊂平面ABCE ，BE ⊂平面ABCE ，且AE BE E =，PE ∴⊥平面ABCE ．又PE ⊂平面PAE ，∴平面PAE ⊥平面ABCE ； （2）解：由（1）得PE ，AE ，CE 两两垂直，故以E 为原点，EC ，EA ，EP 所在直线分别为x ，y ，z 轴建立空间直角坐标系． 则(0A ，2-，0)，(2C ，0，0)，(0P ，0，2)，(4B ，2-，0)．∴(2,0,2)PC =-，(2,2,0)BC =-可知1(1,0,0)n =是平面PAE 的一个法向量，设平面PBC 的一个法向量为2(,,)n x y z =．由22220220n PC x z n BC x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩，取1z =，得2(1,1,1)n =．1212123cos,3||||n n n n n n ⋅∴<>==⋅．10．已知长方形ABCD 中，1AB =，2AD ，现将长方形沿对角线BD 折起，使AC a =，得到一个四面体A BCD -，如图所示．（1）试问：在折叠的过程中，异面直线AB 与CD ，AD 与BC 能否垂直？若能垂直，求出相应的a 值；若不垂直，请说明理由．（2）当四面体A BCD -体积最大时，求二面角A CD B --的余弦值．【解答】解：（1）若AB CD ⊥，由AB AD ⊥，ADCD D =，得AB ⊥面ACD ，AB AC ∴⊥，222AB a BC ∴+=，即212a +=，解得1a =， 若AD BC ⊥，由AB AD ⊥，ABBC B =，得AD ⊥平面ABC ，AD AC ∴⊥，222AD a CD ∴+=，即221a +=，解得21a =-，不成立，AD BC ∴⊥不成立．（2）四面体A BCD -体积最大，BCD ∆2，∴只需三棱锥A BCD -的高最大即可，此时面ABD ⊥面BCD ，以A 为原点，在平面ACD 中过O 作BD 的垂线为x 轴，OD 为y 轴，OA 为z 轴，建立空间直角坐标系，则(0A ，06)，63(,C ，0)，(0D 23，0)， 面BCD 的法向量为(0OA =，06， 面ACD 的法向量(n x =，y ，)z ，63(3CD =-，236(0,)DA =，则630323603n CD x y n DA y ⎧=-=⎪⎪⎨⎪=-+=⎪⎩，取2y =，得(1,2,2)n =， 设二面角A CD B --的平面角为θ，则26||273cos |cos ,|||||673n OA n OA n OA θ=<>===， ∴二面角A CD B --2711．如图，在长方形ABCD 中，AB π=，2AD =，E 、F 为线段AB 的三等分点，G 、H 为线段DC 的三等分点．将长方形ABCD 卷成以AD 为母线的圆柱W 的半个侧面，AB 、CD 分别为圆柱W 上、下底面的直径．（1）证明：平面ADHF ⊥平面BCHF ；（2）求二面角A BH D --的余弦值．【解答】（本小题满分12分）证明：（1）因为H 在下底面圆周上，且CD 为下底面半圆的直径， 所以DH HC ⊥，又因为DH FH ⊥，且CH FH H =，所以DH ⊥平面BCHF ， 又因为DH ⊂平面ADHF ，所以平面ADHF ⊥平面BCHF ． 解：（2）以H 为坐标原点，分别以HD 、HC 、HF 为x ，y ，z 轴建立空间直角坐标系O xyz -， 设下底面半径为r ，由题r ππ=，所以1r =，2CD =因为G 、H 为DC 的三等分点所以30HDC ∠=︒， 所以在Rt DHC ∆中，3,1HD HC ==所以(3,0,2)A ，(0B ，1，2)，(3,0,0)D ， 设平面ABH 的法向量(,,)n x y z=，因为(,,)(3,0,2)0n HA x y z ==， (,,)(0,1,2)0n HB x y z ==，所以2020z y z +=+=⎪⎩，所以平面ABH 的法向量(2,n =--， 设平面BHD 的法向量(,,)m x y z =， 因为(,,)(3,0,0)0m HD x y z ==，(,,)(0,1,2)0m HB x y z ==所以020x y z =⎧⎨+=⎩，所以平面BHD 的法向量(0,2,1)m =-． 所以二面角A BH D --的余弦值为285cos ||||||19m n m n θ==． 12．在菱形ABCD 中，2AB =且60ABC ∠=︒，点M ，N 分别是棱CD ，AD 的中点，将四边形ANMC 沿着AC 转动，使得EF 与MN 重合，形成如图所示多面体，分别取BF ，DE 的中点P ，Q ．（1）求证：//PQ 平面ABCD ；（2）若平面AFEC ⊥平面ABCD ，求多面体ABCDFE 的体积．【解答】解：（1）证明：取BE 中点R ，连接PR ，QR ，BD ，由P ，Q 分别是BF ，DE 的中点， //PR EF ∴，//QR BD ，又//EF AC ，//PR ∴平面ABCD ，//QR 平面ABCD ，又PRQR R =， ∴平面//PQR 平面ABCD ，又PQ ⊂平面PQR ， //PQ ∴平面ABCD ．（2）解：连接AC ，设AC ，BD 交于点O ，BD AC ∴⊥，又平面AFEC ⊥平面ABCD ，平面AFEC ⋂平面ABCD AC =， BD ∴⊥平面AFEC ．∴多面体ABCDFE 可以分解为四棱锥B ACEF -和四棱锥D ACEF -，菱形ABCD 中，2AB =且60ABC ∠=︒知：2AC =，BD =12AC EF ==， 设梯形EFAC 的面积为133()244EFAC BD S EF AC =+=， ∴多面体ABCDFE 的体积为1332ABCDFE EFAC V S BD ==．13．已知等腰直角△S AB '，4S A AB '==，S A AB '⊥，C ，D 分别为S B '，S A '的中点，将△S CD '沿CD 折到SCD ∆的位置，22SA =，取线段SB 的中点为E ．()I 求证：//CE 平面SAD ； （Ⅱ）求二面角A EC B --的余弦值．【解答】（Ⅰ）证明：取SA 中点F ，连接DF ，EF ，SE EB =，SF FA =，//EF AB ∴，12EF AB =， 又//CD AB ，12CD AB =， CD EF ∴=，//CD EF ，∴四边形CDEF 为平行四边形，则//CE FD ．CE ⊂/平面SAD ，FD ⊂平面SAD ，//CE ∴平面SAD ；（Ⅱ）解：面SCD ⊥面ABCD ，面SCD ⋂面ABCD CD =，SD CD ⊥，SD ⊂面SCD ，SD ∴⊥面ABCD ， AD ，CD ⊂面ABCD ，SD AD ∴⊥，SD CD ⊥．又AD DC ⊥，DA ∴，DC ，DS 两两互相垂直，如图所示，分别以DA ，DC ，DS 为x ，y ，z 轴建立空间直角坐标系D xyz -． 则(2A ，0，0)，(0C ，2，0)，(0S ，0，2)，(2B ，4，0)，(1E ，2，1)， (1,0,1)CE =，(2,2,0)CA =-，(2,2,0)CB =， 设平面ECA ，平面ECB 的法向量分别为111(,,)m x y z =，222(,,)n x y z =， 则11110220m CE x z m CA x y ⎧=+=⎪⎨=-=⎪⎩，取11y =，可得(1,1,1)m =-； 22220220n CE x y n CB x y ⎧=+=⎪⎨=+=⎪⎩，取21y =-，得(1,1,1)n =--． 111cos ,||||33m n m n m n -+∴<>===⨯． ∴二面角A EC B --的平面角的余弦值为13-．。