内插法的计算原理(图解)
- 格式:doc
- 大小:104.00 KB
- 文档页数:3

内插法计算方法内插法是一种常用的数值计算方法,它常用于求解函数在给定区间内的根。
内插法的基本思想是通过已知函数值构造一个插值多项式,然后利用这个多项式来近似求解函数的根。
在实际应用中,内插法通常以线性插值、拉格朗日插值和牛顿插值等形式出现。
首先,我们来介绍一下线性插值法。
线性插值法是内插法中最简单的一种,它假设函数在给定区间内是线性变化的。
设有函数f(x),在区间[a, b]上已知两个点的函数值f(a)和f(b),则可以通过线性插值的方式来近似求解函数f(x)在[a, b]上的根。
具体的计算方法是利用已知点(a, f(a))和(b, f(b))构造出一条直线,然后求出这条直线与x轴的交点,即可得到函数f(x)在区间[a, b]上的根的近似值。
接下来,我们介绍一种更为常用的插值方法——拉格朗日插值法。
拉格朗日插值法是一种基于拉格朗日插值多项式的内插法,它可以通过已知函数值构造出一个高次多项式来近似求解函数的根。
设有函数f(x),在区间[a, b]上已知n+1个点的函数值f(x0),f(x1), ..., f(xn),且这n+1个点两两不相等,那么可以构造出一个n次的拉格朗日插值多项式L(x),它满足在这n+1个点上的函数值与f(x)相等。
然后,可以通过求解这个插值多项式的根来近似求解函数f(x)在区间[a, b]上的根。
最后,我们介绍一种更为通用的插值方法——牛顿插值法。
牛顿插值法是一种基于牛顿插值多项式的内插法,它可以通过已知函数值构造出一个高次多项式来近似求解函数的根。
设有函数f(x),在区间[a, b]上已知n+1个点的函数值f(x0), f(x1), ..., f(xn),且这n+1个点两两不相等,那么可以构造出一个n次的牛顿插值多项式N(x),它满足在这n+1个点上的函数值与f(x)相等。
然后,可以通过求解这个插值多项式的根来近似求解函数f(x)在区间[a, b]上的根。
综上所述,内插法是一种常用的数值计算方法,它可以通过已知函数值构造出一个插值多项式来近似求解函数的根。
内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。

内插法的计算公式在数学和金融等领域,内插法是一种常用的计算方法,它能够帮助我们在已知的数据点之间估算未知的值。
内插法的应用范围广泛,从科学研究到金融分析,都能看到它的身影。
那什么是内插法呢?简单来说,就是在已知的两个点之间,根据一定的规律和假设,推测出中间未知点的值。
为了实现这个目的,我们需要用到内插法的计算公式。
内插法的基本原理基于线性关系。
假设我们有两个已知点(x₁, y₁) 和(x₂, y₂),现在要估算一个位于 x₁和 x₂之间的 x 所对应的 y 值。
内插法的计算公式为:y = y₁+(y₂ y₁) /(x₂ x₁) ×(xx₁)我们来逐步拆解这个公式,以便更好地理解。
首先,(y₂ y₁) /(x₂ x₁) 这个部分表示的是两个已知点之间的斜率。
斜率反映了数据的变化趋势。
然后,(x x₁) 表示我们要估算的点与已知点x₁之间的水平距离。
最后,将这两个部分相乘,就得到了在这个斜率下,水平距离所对应的垂直变化量。
再加上 y₁,就得到了估算的 y 值。
为了更直观地理解内插法的计算公式,我们来看一个实际的例子。
假设某商品的价格与销售量之间存在一定的关系。
已知当价格为 10 元时,销售量为 500 件;当价格为 15 元时,销售量为 300 件。
现在我们想知道当价格为 12 元时,销售量大概是多少。
首先,x₁= 10,y₁= 500,x₂= 15,y₂= 300。
斜率=(300 500) /(15 10) =-40然后,x = 12,x₁= 10垂直变化量=-40 ×(12 10) =-80最后,y = 500 +(-80) = 420所以,当价格为 12 元时,估计销售量为 420 件。
内插法不仅在简单的线性关系中有用,在一些稍微复杂的情况中,比如曲线关系,也可以通过分段线性化等方法来应用内插法。
再比如,在金融领域,计算债券的到期收益率时,可能会用到内插法。
已知两个不同利率下债券的价格,要估算某个特定价格对应的利率,就可以借助内插法。
内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P 在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。

内插法目录介绍概念原理介绍又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
按特定函数的性质分,有线性内插、非线性内插等;按引数(自变量)个数分,有单内插、双内插和三内插等。
我国古代早就发明了内插法,当时称为招差术,如公元前1世纪左右的《九章算术》中的“盈不足术”即相当于一次差内插(线性内插);隋朝作《皇极历》的刘焯发明了二次差内插(抛物线内插);唐朝作《太衍历》的僧一行又发明了不等间距的二次差内插法;元朝作《授时历》的郭守敬进一步发明了三次差内插法。
在刘焯1000年后,郭守敬400年后,英国牛顿才提出内插法的一般公式。
概念内插法,一般是指数学上的直线内插,利用等比关系,是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种求未知函数其它值的近似计算方法,是一种未知函数,数值内插法逼近求法,天文学上和农历计算中经常用的是白塞尔内插法,可参考《中国天文年历》的附录。
另外还有其他非线性内插法:如二次抛物线法和三次抛物线法。
因为是用别的线代替原线,所以存在误差。
可以根据计算结果比较误差值,如果误差在可以接受的范围内,才可以用相应的曲线代替。
一般查表法用直线内插法计算。
原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
什么是内插法?答:内插法是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种求未知函数其它值的近似计算方法,是一种未知函数,数值逼近求法,天文学上和农历计算中经常用的是白塞尔内插法,可参考《中国天文年历》的附录。

在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
[编辑]数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B 之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
[编辑]求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:[编辑]内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。

评标内插法计算公式举例评标内插法是一种常用的价格评估方法,常用于建设工程招标评标中。
该方法的基本原理是:通过拟合一条直线,根据相关公式计算出工程的造价。
下面举例说明评标内插法的计算公式:
假设有一个建设工程,要计算的单位工程量为Q,根据工程规模,可以确定相关的工程费用,即:
当Q=100时,工程费用为10000元;
当Q=200时,工程费用为20000元;
当Q=300时,工程费用为30000元。
根据以上信息,我们可以绘制出一条折线图,如下所示:[图片]
接下来,我们就可以使用内插法计算出Q=150时的工程费用。
根据内插法的计算公式,我们需要计算出Q=150时的折现值和Q=150时的内插值。
折现值的计算公式为:
Y=Y1+K*(X-X1)
其中,Y1表示已知的工程费用,X1表示已知的单位工程量,K表示折现系数,X表示待计算的单位工程量,Y表示折现值。
内插值的计算公式为:
Y=Y1+K*(X-X1)+ΔY
其中,ΔY表示内插值。
根据上述公式,我们可以计算出Q=150时的折现值和内插值。
假设当Q=150时,折现值为15000元,内插值为2000元。
那么,Q=150时的工程费用就是折现值加上内插值,即15000+2000=17000元。
以上就是评标内插法的计算公式举例。
通过使用该方法,我们可以快速、准确地计算出建设工程的造价。

内插法内插法,一般是指数学上的直线内插,利用等比关系,是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种未知函数其它值的近似计算方法,是一种求未知函数,数值逼近求法,天文学上和农历计算中经常用的是白塞尔内插法,可参考《中国天文年历》的附录。
另外还有其他非线性内插法:如二次抛物线法和三次抛物线法。
因为是用别的线代替原线,所以存在误差。
可以根据计算结果比较误差值,如果误差在可以接受的范围内,才可以用相应的曲线代替。
一般查表法用直线内插法计算。
数学内插法即"直线插入法"。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i 在i1,i2之间,从而P在点A、B之间,故称"直线内插法"。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面结合实例来讲讲内插法在财务管理中的应用。
折叠在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
一般情况下,内含报酬率的计算都会涉及到内插法的计算。
不过一般要分成这样两种情况: 1.如果某一个投资项目是在投资起点一次投入,经营期内各年现金流量相等,而且是后付年金的情况下,可以先按照年金法确定出内含报酬率的估计值范围,再利用内插法确定内含报酬率2.如果上述条件不能同时满足,就不能按照上述方法直接求出,而是要通过多次试误求出内含报酬率的估值范围,再采用内插法确定内含报酬率。

内插法”的原理及举例相关原理如下:“内插法”的原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据,例如:假设与A1对应的数据是B1 , A2对应的数据是B2 , 现在已知与A对应的数据是B , A介于A1和A2之间,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2) 计算得出A 的数值,其中A1 、A2、B1 、B2、B 都是已知数据。
根本不必记忆教材中的公式,也没有任何规定必须 B 12验证如下:根据: (A1-A)/(A1-A2)=(B1-B)/(B1-B2) 可知:(A1-A) = (B1 -B)/(B1- B2) X(A1-A2 )A = A1 - (B1-B)/(B1- B2) X(A1 -A2 )=A1 + (B1 -B)/(B1- B2) X(A2-A1 )【例题】假设2007年12月1日,M公司与N公司签订了一份租赁合同。
合同主要条款如下:( 1 )租赁标的物:塑钢机。
( 2 )起租日:2008 年1 月1 日。
(3 )租赁期:2008年1月1日〜2010年12月31日,共36 个月。
( 4 )租金支付:自租赁开始日每隔6 个月于月末支付租金150000 元。
(5 )该机器的保险、维护等费用均由M 公司负担,估计每年约10000 元。
(履约成本)(6 )机器在2008 年1 月1 日的公允价值为700000 元。
(7)租赁合同规定的利率为7%(6 个月利率)。
(8 )该机器的估计使用寿命为5 年,期满无残值。
承租人采用年限平均法计提折旧。
(9 )租赁期届满时,M 公司享有优惠购买该机器的选择权,购买价为100 元,估计该日租赁资产的公允价值为80000 元。
(10)2009年和2010年两年,M公司每年按该机器所生产的产品的年销售收入的5%向N 公司支付经营分享收入。
(或有租金)此外,假设该项租赁资产不需安装。
要求:(1 )判断M 公司的租赁类型。

直线内插法计算公式-直线内差法计算直线内插法计算公式直线内差法计算在数学和统计学领域,直线内插法(也称为直线内差法)是一种常用的数值计算方法。
它主要用于根据已知的两个数据点来估算位于这两个点之间的未知数据点的值。
直线内插法的基本原理是基于线性关系假设,即认为两个已知数据点之间的数值变化是呈直线趋势的。
让我们先来看一个简单的例子,以便更好地理解直线内插法的概念。
假设我们知道在温度为 10 摄氏度时,某种物质的电阻为 20 欧姆;在温度为 20 摄氏度时,电阻为 30 欧姆。
现在我们想知道当温度为 15 摄氏度时,该物质的电阻是多少。
在这个例子中,我们可以将温度看作自变量(x),电阻看作因变量(y)。
已知的两个数据点分别是(10, 20)和(20, 30)。
直线内插法的计算公式可以表示为:\y = y_1 +\frac{(y_2 y_1)}{(x_2 x_1)}\times (x x_1)\其中,\(y\)是我们要求的未知值,\(y_1\)和\(y_2\)分别是已知的两个因变量的值,\(x_1\)和\(x_2\)分别是对应的自变量的值,\(x\)是我们要估算的自变量的未知值。
回到刚才的电阻例子,\(x_1 = 10\),\(y_1 = 20\),\(x_2 = 20\),\(y_2 = 30\),\(x = 15\)。
首先计算斜率:\(\frac{(y_2 y_1)}{(x_2 x_1)}=\frac{(30 20)}{(20 10)}= 1\)然后代入公式计算:\y = 20 + 1 \times (15 10) = 20 + 5 = 25\所以,当温度为 15 摄氏度时,该物质的电阻估计为 25 欧姆。
直线内插法在实际应用中非常广泛。
比如在实验数据处理中,如果我们只测量了有限的几个数据点,但需要了解中间未测量点的值,就可以使用直线内插法进行估算。
在金融领域,预测股票价格的走势、计算债券的收益率等也可能会用到直线内插法。

内插法的定义及计算公式内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
内插法-原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法-具体方法(图)内插法内插法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:(图)内插法A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:(图)内插法(图)内插法内插法-计算(图)内插法内插法内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
一般情况下,内含报酬率的计算都会涉及到内插法的计算。
不过一般要分成这样两种情况:1.如果某一个投资项目是在投资起点一次投入,经营期内各年现金流量相等,而且是后付年金的情况下,可以先按照年金法确定出内含报酬率的估计值范围,再利用内插法确定内含报酬率2.如果上述条件不能同时满足,就不能按照上述方法直接求出,而是要通过多次试误求出内含报酬率的估值范围,再采用内插法确定内含报酬率。
内插法简单计算公式
内插法是一种常用的数值计算方法,它可以通过已知数据点的函数值来估计未知数据点的函数值。
内插法的基本思想是在已知数据点之间插入一个函数,然后利用这个函数来计算未知数据点的函数值。
内插法的计算公式比较简单,下面我们来详细介绍一下。
内插法的计算公式可以表示为:
f(x) = f(x0) + (x - x0) * [f(x1) - f(x0)] / (x1 - x0)
其中,f(x) 表示要计算的未知数据点的函数值,x0 和x1 分别表示已知数据点的横坐标,f(x0) 和f(x1) 分别表示已知数据点的纵坐标。
这个公式的意思是,我们可以通过已知数据点的函数值来估计未知数据点的函数值,具体的计算方法是将未知数据点的横坐标代入公式中,然后计算出对应的纵坐标。
内插法的计算公式比较简单,但是要注意一些细节问题。
首先,我们需要保证已知数据点的横坐标是有序的,也就是说x0 < x1。
其次,我们需要保证未知数据点的横坐标在已知数据点的横坐标范围内,否则计算结果可能不准确。
最后,我们需要注意计算精度的问题,尤其是在计算斜率的时候,需要避免除以零的情况。
内插法是一种非常实用的数值计算方法,它可以用来估计未知数据点的函数值,从而帮助我们更好地理解和分析数据。
在实际应用中,
内插法常常被用来处理实验数据、建立数学模型、预测未来趋势等。
因此,掌握内插法的计算公式和使用方法对于我们的学习和工作都非常重要。
附件1:
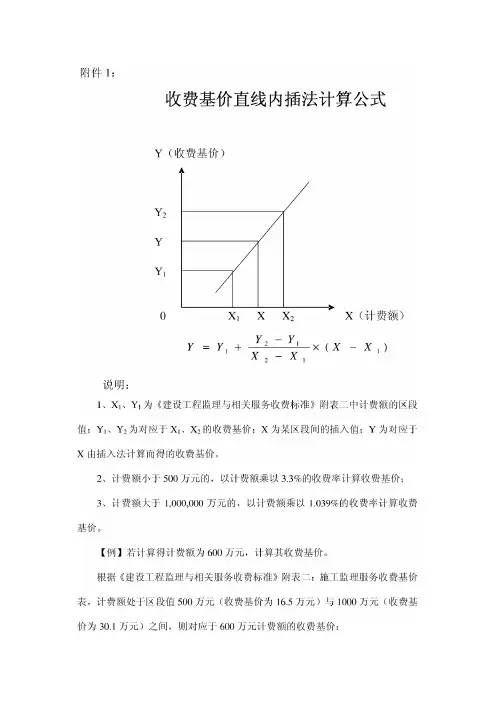
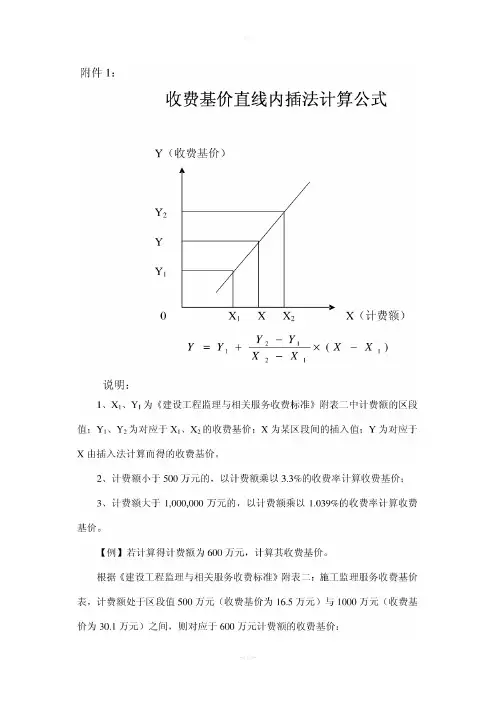
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明: 1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y 1、Y 2为对应于X 1、X 2的收费基价;X 为某区段间的插入值;Y 为对应于X 由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以3.3%的收费率计算收费基价;
3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为16.5万元)与1000万元(收费基价为30.1万元)之间,则对应于600万元计费额的收费基价:
Y (收费基价) Y 2 Y Y 1 0
12 X (计费额)
万元)(22.19)500600(500
10005.161.305.16=-⨯--+=Y。
内插法计算公式及例题1. 什么是内插法?内插法是一种数值计算方法,用于在已知数据点的基础上,通过插值来推算在数据点外部的值。
它广泛应用于物理、工程、地理、金融等领域中。
常见的内插法有拉格朗日内插法、牛顿内插法等。
2. 拉格朗日内插法计算公式假设已有 n+1 个数据点(x0,y0), (x1,y1), …… (xn,yn),那么拉格朗日插值多项式的形式为L(x)= y0L0(x) + y1L1(x) + …… + ynLn(x)其中,Ln(x)=∏i≠n(xi-x)/(xn-xi)L0(x), L1(x), ……, Ln(x)都是x的一次多项式。
例如,已知以下数据点:x | 1 | 3 | 6 | 9 | 12----------------------------------y | 3 | 5 | 2 | 7 | 1那么可以得到拉格朗日插值多项式为:L(x) = 3(-1/4)x^4 + 2x^3 + 9/4x^2 - 15/4x + 3用这个多项式可以估算出在 x=4 或 x=7.5 时的 y 值。
3. 牛顿内插法计算公式牛顿内插法也是一种常见的内插法,它的插值多项式为:f(x) = f(x0) + f[x0,x1](x-x0) + f[x0,x1,x2](x-x0)(x-x1) + …… +f[x0,x1,…,xn](x-x0)(x-x1)……(x-xn-1)其中,f[x0,x1], f[x0,x1,x2], ……, f[x0,x1,…,xn]是用递推算法求出的差商,它们可以表示为:f[xi] = fif[xi,xi+1] = (fi+1 - fi) / (xi+1 - xi)f[xi,…,xi+k] = (f[xi+1,… xi+k] - f[xi,…,xi+k-1]) / (xk - x0)例如,已知以下数据点:x | 4 | 10 | 15 | 20 | 22------------------------------------y | 2 | 5 | 10 | 15 | 20那么可以得到牛顿插值多项式为:f(x) = 2 + 0.25(x-4) + 0.088(x-4)(x-10) + 0.038(x-4)(x-10)(x-15) + 0.025(x-4)(x-10)(x-15)(x-20)用这个多项式可以估算出在 x=12 或 x=18 时的 y 值。
装配式比例内插法
(1)“内插法”的原理是根据等比关系建立一个方程,然后解
方程计算得出所要求的数据。
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,A
介于A1和A2之间,已知与A对应的数据是B,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值。
(2)仔细观察一下这个方程会看出一个特点,即相对应的数据
在等式两方的位置相同。
例如:A1位于等式左方表达式的分子和分
母的左侧,与其对应的数字B1位于等式右方的表达式的分子和分母
的左侧。
(3)还需要注意的一个问题是:如果对A1和A2的数值进行交换,则必须同时对B1和B2的数值也交换,否则,计算得出的结果一定不正确。
内插法的计算式子可以有很多样子,只有保持等式两边对应即可。
500小时处在480小时和540小时两个数字之间,而480对应的修理费为493,540对应的为544,那么根据内插法,500小时对应的数字为x。
就可以列方程为:(500-480)/(540-480)=(x-493)/(544-493),解这个方程,即可得出500小时对应的修理费。
将上面的式子变形,得出X=493+(500-480)/(540-480)*(544-493)。