内插法计算公式(自动计算)

计算设计费内插法计算公式在设计行业中，设计费的计算是一个非常重要的环节。

设计费的计算不仅涉及到设计师的工作量和设计成果的价值，还需要考虑到市场行情和客户的预算。

内插法是一种常用的计算方法，通过内插法可以更准确地计算出设计费，满足设计师和客户双方的需求。

内插法是一种数学计算方法，通过已知数据点之间的关系，推导出未知数据点的数值。

在设计费的计算中，内插法可以用来根据已知的设计项目的费用和规模，推导出新项目的设计费用。

内插法的计算公式如下：设已知数据点为(x1, y1)和(x2, y2)，要求解x对应的y值，则内插法的计算公式为：y = y1 + (x x1) (y2 y1) / (x2 x1)。

其中，x为待求解的设计项目规模，y为对应的设计费用，x1和x2分别为已知设计项目的规模，y1和y2分别为已知设计项目的费用。

内插法的计算步骤如下：1. 确定已知数据点，首先需要确定已知的设计项目的规模和费用，这些数据点将作为内插法计算的基础。

2. 计算斜率，根据已知数据点，计算出斜率，即(y2 y1) / (x2 x1)的值。

3. 计算设计费用，根据内插法的计算公式，将待求解的设计项目规模代入公式中，计算出对应的设计费用。

内插法的优点是可以根据已知数据点的规模和费用，推导出新项目的设计费用，能够更准确地反映设计项目的实际情况。

在实际应用中，设计师和客户可以根据内插法计算出的设计费用进行商议和协商，以达成双方都满意的设计费用。

在使用内插法计算设计费用时，需要注意以下几点：1. 数据点的选择，已知的设计项目规模和费用需要具有代表性和可比性，以确保内插法计算的准确性。

2. 斜率的计算，斜率的计算需要准确无误，是内插法计算的关键步骤。

3. 实际情况的考虑，设计费用的计算不仅仅是数学计算，还需要考虑到实际的市场行情和客户的预算，设计师需要在内插法计算的基础上进行合理的调整。

总之，内插法是一种常用的设计费用计算方法，通过内插法可以更准确地计算出设计项目的费用，满足设计师和客户双方的需求。

收费基价直线内插法计算公式y=y1+ （x-x1）注：1）x1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；y1、y2为对应于x 1、x 2的收费基价；x为某区段间的插入值；y为对应于x由插入法计算而得的收费基价。

「例」若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万（收费基价为16.5万）与1000万（收费基价为30.1万）之间，则对应于600万计费额的收费基价y=16.5+ ×（600-500）＝19.22（万）电力设计一般不打折国家20XX年出了设计收费标准1亿元投资设计300万送变电增加难度系数1.2倍投资小比例高投资大比例小如果只是一个变电所投资额的 4.5％是可能的而且一般由供电部门指定设计某一建筑工程项目总概算为17000万元，其中建筑安装工程费、设备与工器具购置费及联合试运转费之和为9600万元，设计费的计算步骤如下：（1）第一步：计算“基本设计收费”。

基本设计收费是指在工程设计中对所编制的初步设计文件和施工图设计文件收取的费用，并提供相应的设计技术交底、解决施工中的设计技术问题、参加试车考核和竣工验收等服务。

计算公式为：J= Y×t1×t2×t3式中：J——基本设计收费；Y——工程设计收费基价；t1——专业调整系数；t2——工程复杂程度调整系数；t3——附加调整系数。

该建筑工程项目专业调整系数t1＝1.0，工程复杂程度为复杂（III级），工程复杂调整系数t2＝1.15，附加调整系数t3＝1.0。

其中：式中：Y——工程设计收费基价；Y2——Y所在区间上限；Y1——Y所在区间下限；X——工程设计收费计费额；X2——X所在区间上限；X1——X所在区间上限。

工程设计收费计费额为经过批准的建设项目初步设计概算中的建筑安装工程费、设备与工器具购置费及联合试运转费之和。

１
附件二
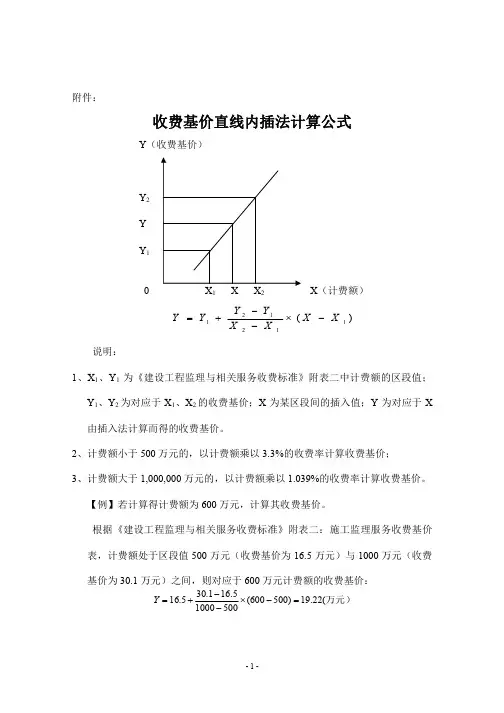
收费基价直线内插法计算公式
y=y 1+ (x-x 1)
注：
1）x 1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；y 1、y 2为对应于x 1、x 2的收费基价；x 为某区段间的插入值；y 为对应于x 由插入法计算而得的收费基价。

2）计费额小于500万元的，以计费额乘以3.3％的收费率计算收费基价； 3）计费额大于1，000，000万元的，以计费额乘以1.039％的收费率计算收费基价。

【例】若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万（收费基价为16.5万）与1000万（收费基价为30.1万）之间，则对应于600万计费额的收费基价
y=16.5+ ×(600-500)＝19.22（万）
（计费额）
（收费基价）
y 2-y 1
x 2-x 1
30.1-16.5
1000-500
附件三
2
建设工程监理与相关服务价格违法违规行为处罚标准和处罚依据
3。

收费基价直线内插法计算公式y=y1+ （x-x1）注：1）x1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；y1、y2为对应于x 1、x 2的收费基价；x为某区段间的插入值；y为对应于x由插入法计算而得的收费基价。

「例」若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万（收费基价为16.5万）与1000万（收费基价为30.1万）之间，则对应于600万计费额的收费基价y=16.5+ ×（600-500）＝19.22（万）电力设计一般不打折国家20XX年出了设计收费标准1亿元投资设计300万送变电增加难度系数1.2倍投资小比例高投资大比例小如果只是一个变电所投资额的 4.5％是可能的而且一般由供电部门指定设计某一建筑工程项目总概算为17000万元，其中建筑安装工程费、设备与工器具购置费及联合试运转费之和为9600万元，设计费的计算步骤如下：（1）第一步：计算“基本设计收费”。

基本设计收费是指在工程设计中对所编制的初步设计文件和施工图设计文件收取的费用，并提供相应的设计技术交底、解决施工中的设计技术问题、参加试车考核和竣工验收等服务。

计算公式为：J= Y×t1×t2×t3式中：J——基本设计收费；Y——工程设计收费基价；t1——专业调整系数；t2——工程复杂程度调整系数；t3——附加调整系数。

该建筑工程项目专业调整系数t1＝1.0，工程复杂程度为复杂（III级），工程复杂调整系数t2＝1.15，附加调整系数t3＝1.0。

其中：式中：Y——工程设计收费基价；Y2——Y所在区间上限；Y1——Y所在区间下限；X——工程设计收费计费额；X2——X所在区间上限；X1——X所在区间上限。

工程设计收费计费额为经过批准的建设项目初步设计概算中的建筑安装工程费、设备与工器具购置费及联合试运转费之和。

内插法的计算公式在数学和金融等领域，内插法是一种常用的计算方法。

它能够帮助我们在已知的数据点之间估算出未知的值，具有广泛的应用场景。

接下来，让我们一起深入了解内插法的计算公式及其原理。

内插法，简单来说，就是在一系列已知的数据点之间，通过一定的数学方法，推测出中间未知的数据点的值。

这种方法基于数据的连续性和趋势性假设。

我们先来看一个简单的线性内插法的例子。

假设有两个已知点，点A 的坐标为（x1, y1)，点B 的坐标为（x2, y2)，现在要在 x1 和 x2 之间的某个 x 值处求出对应的 y 值。

线性内插法的计算公式为：＼y ＝ y1 ＋＼frac{（x x1)（y2 y1)｝｛（x2 x1)｝＼这个公式的含义是，首先计算出两个已知点之间的斜率，即＼（（y2 y1) ／（x2 x1)＼），然后根据所求点与已知点 x 坐标的差值，乘以斜率，再加上起始点的 y 值，就得到了所求点的 y 值。

为了更好地理解这个公式，我们通过一个具体的例子来演示。

假设点 A 的坐标为（1, 3)，点 B 的坐标为（5, 9)，现在要求出 x ＝ 3 时对应的 y 值。

首先，计算斜率：＼（（9 3) ／（5 1) ＝ 15\）然后，代入公式：＼y ＝ 3 ＋＼frac{（3 1)×（9 3)｝｛（5 1)｝＝ 3 ＋＼frac{2×6}｛4} ＝ 3 ＋ 3 ＝ 6\所以，当 x ＝ 3 时，y 的值为 6 。

除了线性内插法，还有更复杂的非线性内插法，比如二次内插法、三次内插法等。

二次内插法适用于数据呈现出抛物线形状的情况。

假设我们有三个已知点 A(x1, y1)、B(x2, y2)、C(x3, y3)，通过构建一个二次函数来进行内插。

二次内插法的一般公式为：＼y ＝ a(x x2)（x x3) ＋ b(x x1)（x x3) ＋ c(x x1)（x x2)＼其中，a、b、c 是通过已知点的坐标计算得出的系数。

１
作者：空青山
作品编号：89964445889663Gd53022257782215002 时间：2020.12.13
附件二
收费基价直线内插法计算公式
y=y 1+ (x-x 1)
注：
1）x 1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；y 1、y 2为对应于x 1、x 2的收费基价；x 为某区段间的插入值；y 为对应于x 由插入法计算而得的收费基价。

2）计费额小于500万元的，以计费额乘以3.3％的收费率计算收费基价； 3）计费额大于1，000，000万元的，以计费额乘以1.039％的收费率计算收费基价。

【例】若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万（收费基价为16.5万）与
（计费额）
（收费基价）
y 2-y 1
x 2-x 1
30.1-16.5
1000-500
1000万（收费基价为30.1万）之间，则对应于600万计费额的收费基价
y=16.5+ ×(600-500)＝19.22（万）
２
附件三
3
建设工程监理与相关服务价格违法违规行为处罚标准和处罚依据
作者：空青山
作品编号：89964445889663Gd53022257782215002
时间：2020.12.13
4。

内插法的计算公式在数学和金融等领域，内插法是一种常用的计算方法，它能够帮助我们在已知数据点之间估算未知的值。

内插法的应用场景广泛，比如在金融领域用于计算债券的收益率，在工程领域用于估算不同条件下的测量值等。

接下来，让我们详细了解一下内插法的计算公式及其原理。

内插法，简单来说，就是在一组已知的数据点之间，通过建立某种数学关系，来推测出位于这些数据点之间的未知数据。

其核心思想是假设数据之间存在某种线性或非线性的关系，并基于这种假设进行计算。

我们先从线性内插法说起。

线性内插法是内插法中最简单也最常用的一种形式。

假设我们有两个已知数据点（x1, y1) 和（x2, y2)，现在要估算位于 x1 和 x2 之间的某个 x 值所对应的 y 值。

线性内插法的计算公式为：y ＝ y1 ＋（（x x1) （y2 y1) ／（x2 x1)）为了更好地理解这个公式，我们通过一个具体的例子来说明。

假设某商品的价格在 1 月份为 100 元，2 月份为 120 元。

现在我们想知道在1 月 15 日时该商品的价格。

在这里，x1 ＝ 1（代表 1 月份），y1 ＝ 100；x2 ＝ 2（代表 2 月份），y2 ＝ 120；x ＝ 15（代表 1 月 15 日）。

将这些值代入公式：y ＝ 100 ＋（（15 1) （120 100) ／（2 1)）＝ 100 ＋（05 20) ＝ 110 元。

所以，通过线性内插法，我们估算出 1 月 15 日该商品的价格约为110 元。

除了线性内插法，还有非线性内插法，比如二次内插法和三次内插法等。

二次内插法假设数据之间的关系是二次函数形式。

其计算公式相对复杂，需要先根据三个已知数据点确定二次函数的系数，然后再代入要估算的 x 值计算出对应的 y 值。

三次内插法则假设数据之间的关系是三次函数形式，计算过程更为繁琐。

在实际应用中，选择哪种内插法取决于数据的特点和精度要求。

如果数据呈现出明显的线性趋势，那么线性内插法通常就能够满足需求。

内插法计算公式内插法计算公式1、X1、Y1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y1、Y2为对应于X1、X2的收费基价;X为某区段间的插入值道;Y为对应于X由插入法计算而得的收费基价。

2、计费额小于500万元的,以计费额乘以3.3%的收费专率计算收费基价;3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。

【例】若计算得计费额为600万元,计算其收费基价属。

根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元（收费基价为16.5万元）与1000万元（收费基价为30.1万元）之间,则对应于600万元计费额的收费基价:内插法（Interpolation Method）什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。

内插法原理数学内插法即“直线插入法”。

其原理是,若A(i1,b1),B(i2,b2)为两点,则点P（i,b)在上述两点确定的直线上。

而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。

数学内插法说明点P反映的变量遵循直线AB反映的线性关系。

上述公式易得。

A、B、P三点共线,则(b-b1)/(i-i1)＝（b2-b1)/(i2-i1)=直线斜率,变换即得所求。

内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。

以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。

直线内插法计算公式
y=y1+(x-x1)*(y2-y1)/(x2-x1)
其中，(x1,y1)和(x2,y2)为已知数据点的坐标，(x,y)为要估算的未知数据点的坐标。

y表示y轴上的值，x表示x轴上的值。

下面以一个简单的例子来说明直线内插法的计算过程。

假设我们已知以下两个数据点：(1,10)和(5,20)。

我们想要估算在x=3时的y值。

根据直线内插法的计算公式：
y=10+(3-1)*(20-10)/(5-1)
=10+2*10/4
=10+20/4
=10+5
=15
因此，在x=3时，y的估算值为15
直线内插法的计算思路很简单，只需要根据已知数据点的坐标和要估算的未知数据点的x值，利用计算公式进行计算即可。

这种方法在实际问题中应用广泛，特别是在数据不连续或不均匀的情况下，可以用来填补数据间的空缺或预测未知数据。

其优点是计算简单、直观易懂，但缺点是在数据变化非常快或非线性的情况下，可能会导致估算结果不准确。

当然，如果已知数据点更多，也可以使用更复杂的插值方法，如多项式插值、样条插值等，以提高估算的精确度。

这些方法的计算公式相对来说更复杂一些，但在实际应用中也有其优势和适用范围。

总之，直线内插法是一种简单而常用的数值计算方法，通过线性插值来估算未知数据点的值。

在实际问题中，可以根据需要选择不同的插值方法来获得更准确的估算结果。

附件二 收费基价直线内插法计算公式
y=y 1+ (x-x 1)
注：
1）x 1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；
y 1、y 2为对应于x 1、x 2的收费基价；x 为某区段间的插入值；y 为对应于x 由插入
法计算而得的收费基价。

2）计费额小于500万元的，以计费额乘以3.3％的收费率计算收费基价； 3）计费额大于1，000，000万元的，以计费额乘以1.039％的收费率计算收费
基价。

【例】若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务
收费基价表，计费额处于区段值500万（收费基价为16.5万）与1000
万（收费基价为30.1万）之间，则对应于600万计费额的收费基价
y=16.5+ ×(600-500)＝19.22（万）
（计费额）
（收费基价） y 2-y 1 x 2-x 1 30.1-16.5
1000-500
附件三
建设工程监理与相关服务价格违法违规行为处罚标准和处罚依据。