ZEMAX软件的优化函数构成以及优化函数算法的心得
- 格式:pdf
- 大小:111.35 KB
- 文档页数:12

优化函数1、像差SPHA(球差):surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的球差贡献值,以波长表示。
如果表面编号值为零,则为整个系统的总和COMA(彗差) :surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级彗差,对非近轴系统无效.ASTI(像散):指定表面产生像散的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效FCUR(场曲):指定表面产生的场曲贡献值,以波长表示。
如果表面编号值为0,则是计算整个系统的场曲。
这是由塞得系数计算出的第三级场曲,对非近轴系统无效.DIST(畸变):指定表面产生的畸变贡献值,以波长表示。
如果表面编号值为0,则使用整个系统。
同样,如果表面编号值为0,则畸变以百分数形式给出。
这是由塞得系数计算出的第三级畸变,对与非近轴系统无效.DIMX(最大畸变值):它与DIST 相似,只不过它仅规定了畸变的绝对值的上限。
视场的整数编号可以是0,这说明使用最大的视场坐标,也可以是任何有效的视场编号。
注意,最大的畸变不一定总是在最大视场处产生。
得到的值总是以百分数为单位,以系统作为一个整体。
这个操作数对于非旋转对称系统可能无效。
AXCL(轴向色差):以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效.LACL(垂轴色差):这是定义的两种极端波长的主光线截点的y方向的距离。
对于非近轴系统无效TRAR(垂轴像差):在像面半径方向测定的相对于主光线的垂轴像差.TRAX(x方向垂轴像差):在像面x方向测定的相对于主光线的垂轴像差TRAY(Y方向垂轴像差):在像面Y方向测定的相对于主光线的垂轴像差TRAI(垂轴像差):在指定表面半口径方向测定的相对于主光线的垂轴像差.类似于TRAR,只不过是针对一个表面,而不是指定的像面.OPDC(光程差):指定波长的主光线的光程差.PETZ(匹兹伐曲率半径):以镜头长度单位表示,对非近轴系统无效PETC(匹兹伐曲率):以镜头长度单位的倒数表示,对非近轴系统无效RSCH:相对于主光线的RMS 斑点尺寸(光线像差)。

ZEMAX优化函数结构浅探ZEMAX是一种光学设计和仿真软件,可以用于光学系统的快速设计和分析。
它的优化功能可以自动光学系统参数的最佳解,以满足设计需求。
ZEMAX中的优化函数结构是一种用于定义优化问题的方式,可以控制算法的行为以及优化过程中参数的变化方式。
在本文中,我们将对ZEMAX优化函数结构进行详细介绍。
优化函数结构包括两个主要部分:自变量和目标函数。
自变量是指需要被优化的系统参数,如曲率半径、物体和像点位置等。
目标函数是用来评估系统性能的指标,如像差、套筒直径等。
通过不断优化自变量,使目标函数达到最小值或最大值,就可以得到最佳的系统参数。
在ZEMAX中,自变量可以分为两类:设计变量和全局变量。
设计变量是指会随着优化过程而改变的参数,如透镜的曲率半径。
全局变量是指不会改变的参数,如透镜的材料和厚度。
ZEMAX提供了多种目标函数类型,可以根据不同的设计需求选择合适的目标函数。
常用的目标函数类型包括像差、光通量、曲率等。
用户可以根据具体的优化目标选择适合的目标函数类型,并根据需要进行自定义。
目标函数可以是一个或多个输出变量的组合,也可以是一些复杂的计算公式。
在ZEMAX中,优化过程是通过算法来实现的。
ZEMAX提供了多种算法,包括遗传算法、模拟退火算法和单纯形法等。
用户可以根据问题的复杂程度和计算资源的限制选择合适的算法。
ZEMAX还提供了一些优化算法参数的设置,如初始解、迭代次数和收敛准则等,可以帮助用户更好地控制优化过程。
在实际应用中,ZEMAX优化函数结构的设计需要考虑以下几个方面。
首先,需要明确系统的设计需求和优化目标,以确定自变量和目标函数的选择。
其次,需要根据具体问题的要求来选择适当的算法,并进行相关参数的设置。
此外,还需要进行多次的优化试验和结果分析,以便找到最佳的系统参数。
总的来说,ZEMAX优化函数结构是一种能够自动最佳解的设计工具,可以在光学系统设计过程中提供快速准确的优化结果。


ZEMAX优化操作数汇总
Zemax有完整的设计、模拟和优化工具组合,这样,您可以使用这些
工具来完成任何光学设计、制造、维护和测试任务。
它的优化功能有助于
加快设计的完成, Zemax优化可以进行整体结构图和衍射正(DPR)优化,可以实现准确、稳定和可控的优化过程,根据实际应用需求来配置最佳优
化策略。
一、基本概念
Zemax优化任务是基于极小化指标、优化变量和优化约束,它可以自
动确定最佳参数来满足用户设定的最小优化指标。
1.优化指标:优化指标是指需要极小化的目标,比如最小化光斑不均
匀度,最大化衍射正反差等。
2.优化变量:优化变量是指需要最佳化的光学系统元素,比如焦距、
衍射正的外径和光学厚度等。
3.优化约束:优化约束是指需要限制的变量的范围,比如限制设计的
光学元件不能超出所选材料的范围、设置变量不能超出最小和最大值等。
二、优化算法
1.基于随机的算法:基于随机的算法是指基于随机策略来可能优化参
数的算法,可以用来最优解,但是需要很多的次数。
2.基于梯度的算法:基于梯度的算法是指基于梯度来实现优化算法,
它可以更充分和快速地最优解。


优化函数1、像差SPHA(球差):surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的球差贡献值,以波长表示。
如果表面编号值为零,则为整个系统的总和COMA(彗差) :surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级彗差,对非近轴系统无效.ASTI(像散):指定表面产生像散的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效FCUR(场曲):指定表面产生的场曲贡献值,以波长表示。
如果表面编号值为0,则是计算整个系统的场曲。
这是由塞得系数计算出的第三级场曲,对非近轴系统无效.DIST(畸变):指定表面产生的畸变贡献值,以波长表示。
如果表面编号值为0,则使用整个系统。
同样,如果表面编号值为0,则畸变以百分数形式给出。
这是由塞得系数计算出的第三级畸变,对与非近轴系统无效.DIMX(最大畸变值):它与DIST 相似,只不过它仅规定了畸变的绝对值的上限。
视场的整数编号可以是0,这说明使用最大的视场坐标,也可以是任何有效的视场编号。
注意,最大的畸变不一定总是在最大视场处产生。
得到的值总是以百分数为单位,以系统作为一个整体。
这个操作数对于非旋转对称系统可能无效。
AXCL(轴向色差):以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效.LACL(垂轴色差):这是定义的两种极端波长的主光线截点的y方向的距离。
对于非近轴系统无效TRAR(垂轴像差):在像面半径方向测定的相对于主光线的垂轴像差.TRAX(x方向垂轴像差):在像面x方向测定的相对于主光线的垂轴像差TRAY(Y方向垂轴像差):在像面Y方向测定的相对于主光线的垂轴像差TRAI(垂轴像差):在指定表面半口径方向测定的相对于主光线的垂轴像差.类似于TRAR,只不过是针对一个表面,而不是指定的像面.OPDC(光程差):指定波长的主光线的光程差.PETZ(匹兹伐曲率半径):以镜头长度单位表示,对非近轴系统无效PETC(匹兹伐曲率):以镜头长度单位的倒数表示,对非近轴系统无效RSCH:相对于主光线的RMS 斑点尺寸(光线像差)。

ZEMAX优化操作数汇总1.各种变量优化:ZEMAX可以对各种变量进行优化,包括系统参数、元件参数和材料参数。
例如,可以对透镜曲面的半径、厚度和折射率进行优化,以获得最佳的成像性能。
2.像差优化:ZEMAX可以优化像差,以最小化系统的像差。
它可以优化球差、彗差、色差、畸变等各种像差,并生成最佳的光学系统。
3.波前优化:ZEMAX可以优化波前,以获得最佳的波前形状。
它可以用于修正各种波前畸变,例如球差、彗差和色差。
4.光斑优化:ZEMAX可以优化光斑,以获得最佳的光斑形状和尺寸。
它可以用于优化点光源的光斑,或者控制光源的光斑形状和尺寸。
5.聚焦优化:ZEMAX可以优化聚焦距离,以获得最佳的聚焦性能。
它可以用于优化透镜或镜片的形状和位置,以实现最佳的聚焦效果。
6.薄透镜优化:ZEMAX可以优化薄透镜的参数,以获得最佳的成像性能。
它可以优化透镜的半径、厚度和折射率,以实现最小的像差。
7.波导优化:ZEMAX可以优化波导的参数,以获得最佳的传输特性。
例如,它可以优化波导的宽度和高度,以实现最小的传输损耗。
8.激光优化:ZEMAX可以优化激光光束的参数,以获得最佳的激光束质量。
例如,它可以优化激光光束的直径和发散角,以实现最小的发散和最高的光束质量。
9.过滤器优化:ZEMAX可以优化过滤器的参数,以获得最佳的滤波特性。
它可以优化过滤器的传输曲线、中心波长和带宽,以实现最佳的滤波效果。
10.微透镜阵列优化:ZEMAX可以优化微透镜阵列的参数,以获得最佳的光学性能。
例如,它可以优化微透镜阵列的尺寸、间距和折射率,以实现最佳的成像和聚焦效果。
总之,ZEMAX提供了许多优化操作数,可以用于不同类型的光学系统的设计和分析。
这些优化操作数可以帮助用户获得最佳的成像性能、波前形状、光斑形状和尺寸、聚焦性能等。

zemax优化函数使用方法Zemax是一款常用于光学系统设计和优化的软件工具。
其中的优化函数是Zemax的一个重要功能,可以帮助用户通过自动搜索和调整系统参数,找到最优的设计方案。
本文将介绍Zemax优化函数的使用方法。
一、什么是优化函数在光学系统设计中,我们通常需要通过调整系统的各种参数来实现特定的设计要求。
而优化函数就是帮助我们在众多参数中找到最优解的工具。
其原理是通过数值计算和模拟,自动化地搜索参数空间,以寻找最佳的设计方案。
二、Zemax中的优化函数Zemax中的优化函数可以分为两大类:单变量优化和多变量优化。
单变量优化是指只有一个参数需要进行调整,而多变量优化则是同时调整多个参数。
下面将分别介绍这两种优化函数的使用方法。
1. 单变量优化函数单变量优化函数可以通过调整一个参数,来寻找最优解。
在Zemax 中,我们可以选择需要调整的参数,并设置其变化的范围和步长。
然后,通过运行优化函数,Zemax会自动搜索参数空间,并给出最优的结果。
2. 多变量优化函数多变量优化函数可以同时调整多个参数,以找到最优解。
在Zemax 中,我们可以选择多个参数,并设置它们的变化范围。
然后,通过运行优化函数,Zemax会自动搜索多个参数的组合,并给出最佳的设计方案。
三、使用优化函数的步骤使用Zemax的优化函数,一般需要按照以下步骤进行操作:1. 定义优化目标:首先,我们需要明确设计的目标和要求,例如最小化像差、最大化光学传输等。
这样才能设置正确的优化函数和参数。
2. 设置参数范围:根据设计要求,我们需要选择需要调整的参数,并设置它们的变化范围。
例如,镜片的曲率半径、透镜的厚度等。
3. 运行优化函数:在Zemax中,我们可以选择不同的优化函数进行计算。
例如,全局优化、局部优化等。
根据设计要求和参数设置,选择适合的优化函数,并运行它。
4. 分析结果:运行完优化函数后,Zemax会给出最优的设计方案。
我们可以通过分析结果,评估设计的优劣,并进行进一步的优化和改进。
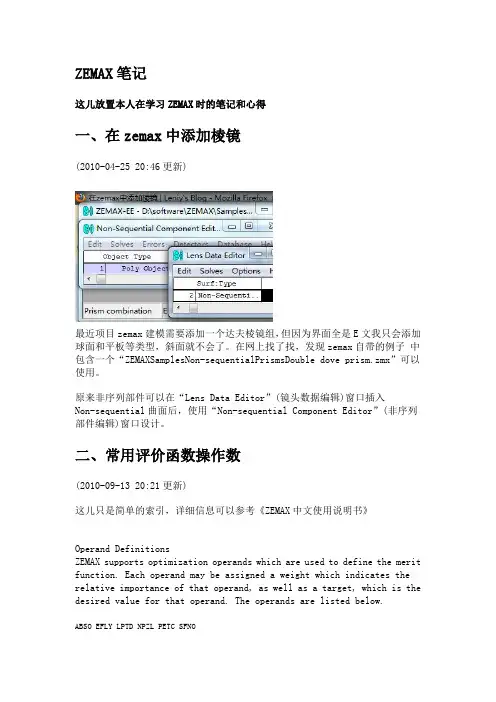
ZEMAX笔记这儿放置本人在学习ZEMAX时的笔记和心得一、在zemax中添加棱镜(2010-04-25 20:46更新)最近项目zemax建模需要添加一个达夫棱镜组,但因为界面全是E文我只会添加球面和平板等类型,斜面就不会了。
在网上找了找,发现zemax自带的例子中包含一个“ZEMA XSamplesNon-sequentialPrismsDouble dove prism.zmx”可以使用。
原来非序列部件可以在“Lens Data Editor”(镜头数据编辑)窗口插入Non-sequential曲面后,使用“Non-sequential Component Editor”(非序列部件编辑)窗口设计。
二、常用评价函数操作数(2010-09-13 20:21更新)这儿只是简单的索引,详细信息可以参考《ZEMAX中文使用说明书》Operand DefinitionsZEMAX supports optimization operands which are used to define the merit function. Each operand may be assigned a weight which indicates the relative importance of that operand, as well as a target, which is the desired value for that operand. The operands are listed below.ABSO EFLY LPTD NPZL PETC SFNOACOS ENDX MAXX NPZV PETZ SINEAMAG ENPP MCOG NSDD PIMH SKINANAR EPDI MCOL NSTR PLEN SKISASIN EQUA MCOV NTXG PMAG SPHAASTI ETGT MINN NTXL POWR SQRTATAN ETLT MNAB NTXV PRIM SUMMAXCL ETVA MNCA NTYG PROD SVIGBLNK EXPP MNCG NTYL QSUM TANGBSER FCGS MNCT NTYV RAGX TFNOCOGT FCGT MNCV NTZG RAGY TMASCOLT FCUR MNDT NTZL RAGZ TOTRCOMA FICL MNEA NTZV RAGA TRACCONF FOUC MNEG NPGT RAGB TRADCONS GBW0 MNET NPLT RAGC TRAECOSI GBWA MNIN NPVA RAED TRAICOVA GBWD MNPD OBSN RAEN TRARCTGT GBWZ MNSD OFF RAID TRAXCTLT GBWR MSWA OPDC RAIN TRAYCTVA GCOS MSWS OPDM RANG TRCXCVGT GENC MSWT OPDX REAA TRCYCVLT GLCA MTFA OPGT REAB TTGTCVOL GLCB MTFS OPLT REAC TTHICVVA GLCC MTFT OPTH REAR TTLTDENC GLCX MXAB OSUM REAX TTVADENF GLCY MXCA PnGT REAY UDOPDIFF GLCZ MXCG PnLT REAZ USYMDIMX GMTA MXCT PnVA RENA VOLUDISC GMTS MXCV PMGT RENB WFNODISG GMTT MXDT PMLT RENC XDGTDIST GPIM MXEA PMVA RETX XDLTDIVI GRMN MXEG PANA RETY XDVADLTN GRMX MXET PANB RGLA XENCDMFS GTCE MXIN PANC RSCE XNEADMGT HHCN MXPD PARA RSCH XNEGDMLT IMAE MXSD PARB RSRE XNETDMVA INDX NPXG PARC RSRH XXEADXDX InGT NPXL PARR RWCE XXEGDXDY InLT NPXV PARX RWCH XXETDYDX InVA NPYG PARY RWRE YNIPDYDY ISFN NPYL PARZ RWRH ZERNEFFL LACL NPYV PATX SAGX ZPLMEFLX LINV NPZG PATY SAGY ZTHI三、默认评价函数优化类型默认优化类型默认优化数据类型默认的优化参考点四、本次光学镜头课程设计所用评价函数五、毕业设计在ZEMAX中模拟薄膜透过率曲线(2011-04-14 23:48更新)最近稍微完善了一下Cauchy和Drude色散模型部分的程序,想要验证一下优化函数的效果。

zemax主要优化函数zemax主要优化函数表2008年07月28日星期一 00:53优化函数1、像差SPHA(球差):surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的球差贡献值,以波长表示。
如果表面编号值为零,则为整个系统的总和COMA(彗差) :surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的贡献值,以波长表示。
如果表面编号值为 0,则是针对整个系统。
这是由塞得和数计算得到的第三级彗差,对非近轴系统无效.ASTI(像散):指定表面产生像散的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效 FCUR(场曲):指定表面产生的场曲贡献值,以波长表示。
如果表面编号值为0,则是计算整个系统的场曲。
这是由塞得系数计算出的第三级场曲,对非近轴系统无效.DIST(畸变):指定表面产生的畸变贡献值,以波长表示。
如果表面编号值为0,则使用整个系统。
同样,如果表面编号值为 0,则畸变以百分数形式给出。
这是由塞得系数计算出的第三级畸变,对与非近轴系统无效.DIMX(最大畸变值):它与 DIST 相似,只不过它仅规定了畸变的绝对值的上限。
视场的整数编号可以是 0,这说明使用最大的视场坐标,也可以是任何有效的视场编号。
注意,最大的畸变不一定总是在最大视场处产生。
得到的值总是以百分数为单位,以系统作为一个整体。
这个操作数对于非旋转对称系统可能无效。
AXCL(轴向色差):以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效. LACL(垂轴色差):这是定义的两种极端波长的主光线截点的y方向的距离。
对于非近轴系统无效TRAR(垂轴像差):在像面半径方向测定的相对于主光线的垂轴像差. TRAX(x方向垂轴像差):在像面x方向测定的相对于主光线的垂轴像差 TRAY(Y方向垂轴像差):在像面Y方向测定的相对于主光线的垂轴像差 TRAI(垂轴像差):在指定表面半口径方向测定的相对于主光线的垂轴像差.类似于 TRAR,只不过是针对一个表面,而不是指定的像面.OPDC(光程差):指定波长的主光线的光程差.PETZ(匹兹伐曲率半径):以镜头长度单位表示,对非近轴系统无效 PETC(匹兹伐曲率):以镜头长度单位的倒数表示,对非近轴系统无效 RSCH:相对于主光线的RMS 斑点尺寸(光线像差)。
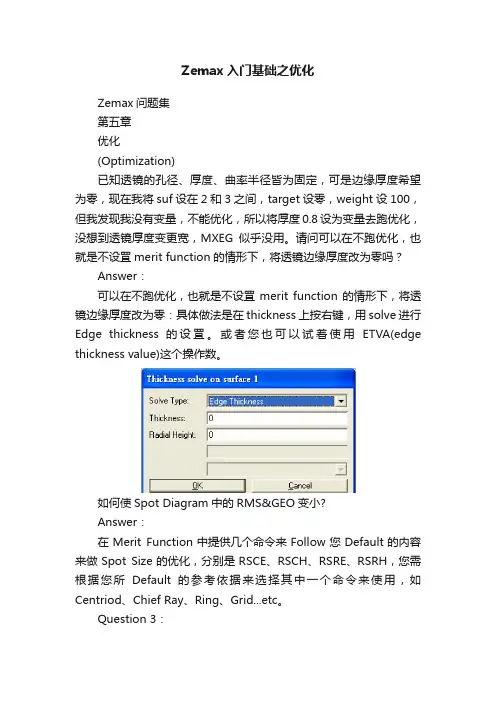
Zemax入门基础之优化Zemax问题集第五章优化(Optimization)已知透镜的孔径、厚度、曲率半径皆为固定,可是边缘厚度希望为零,现在我将suf设在2和3之间,target设零,weight设100,但我发现我没有变量,不能优化,所以将厚度0.8设为变量去跑优化,没想到透镜厚度变更宽,MXEG似乎没用。
请问可以在不跑优化,也就是不设罝merit function的情形下,将透镜边缘厚度改为零吗?Answer:可以在不跑优化,也就是不设罝merit function的情形下,将透镜边缘厚度改为零:具体做法是在thickness上按右键,用solve进行Edge thickness 的设罝。
或者您也可以试着使用ETVA(edge thickness value)这个操作数。
如何使Spot Diagram中的RMS&GEO变小?Answer:在Merit Function中提供几个命令来Follow您Default的内容来做Spot Size的优化,分别是RSCE、RSCH、RSRE、RSRH,您需根据您所Default的参考依据来选择其中一个命令来使用,如Centriod、Chief Ray、Ring、Grid...etc。
Question 3:在优化过程中,如何定义在不同Pupil的地方,其Longitudinal Aberration曲线可以依照自己的意思跑吗?Answer:当在使用AXCL和LACL等命令时,无法使用Hx、Hy、Px、Py 来控制实际光线所走的路径,此时会是一类型似默认的方法来达到优化,通常在Pupil的0.8处有交点,但若当您使用REAY等命令时,您可在Py的地方给定0~1的值,即代表您希望在Pupil上的某个点所出射的光线其Longitudinal Aberration会最小,即可在不同的Pupil处依您的意思去做优化。
如何使用ZEMAX的功能来分析镜头的TV Distortion?Answer:关于TV Distortion的分析同样可使用ZEMAX的分析功能,分析功能在Anaylsis->Miscellaneous->Field Curv/Dist和Grid Distortion。
Zemax-光学系统设计经验(1)---优化函数的使用使用Zemax设计光学系统,基本上就是根据设计要求,给出初始设计,然后优化系统。
初始设计需要对光学有系统的学习,需要长期的经验,不同的领域有不同的要求,初始设计会大不相同,zemax不会给你太多的帮助。
Zemax的精髓是能计算出光路图,然后使用operand(优化函数)优化各项光学参数。
1. default merit function,当属最有用的优化函数,配合EFFL (有效焦距)使用,基本可以设计大部分光学系统。
可以使用RMS spot radius and rms wavefront error。
另外设置好变量。
Zemax会自动生成优化系数(weight). 函数行的量取决于波长数,场(field)数,也决定了计算的快慢。
2. 自己设计优化函数。
第一步,需要知道你的优化目标:焦距,abberation,耦合效率。
设置好constraints.设计的constraints:Lens size, cost; edge and center thickeness; minimum number of lens; simple design; cheap举例来讲,耦合效率。
有两个最有用的函数:FICL, POPD. 前者快,后者慢,但后者对大多数系统要准确一些。
读一下manual,你会知道你要设置什么参数。
优化目标是1,weight 是1. 要知道在哪个surface上,还有在什么wavelength, field, 最重要的是什么优化数据,可以是耦合效率,也可以是beam size。
如果都要考虑,可以设置新的POPD函数,设置好优化系数(weight). 有例子,改一下merit function就可以了。
有些有用的优化函数:加减乘除:SUMM, DIFF, PROD,DIVI镜头数据:MXCG, MNCG, CTGT, MNCT,变量的设置也很有讲究,越多越靠近理想目标,但是降低速度和提高坏设计的几率.几点经验:1. 尽可能 use solve, instead of 变量2. 尽可能 use default merit function3. 理解constraints4. 理解和使用symmetry5. 去掉无用的变量.6. 知道怎么去改变设计。
优化函数1、像差SPHA(球差):surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的球差贡献值,以波长表示。
如果表面编号值为零,则为整个系统的总和COMA(彗差) :surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级彗差,对非近轴系统无效.ASTI(像散):指定表面产生像散的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效FCUR(场曲):指定表面产生的场曲贡献值,以波长表示。
如果表面编号值为0,则是计算整个系统的场曲。
这是由塞得系数计算出的第三级场曲,对非近轴系统无效.DIST(畸变):指定表面产生的畸变贡献值,以波长表示。
如果表面编号值为0,则使用整个系统。
同样,如果表面编号值为0,则畸变以百分数形式给出。
这是由塞得系数计算出的第三级畸变,对与非近轴系统无效.DIMX(最大畸变值):它与DIST 相似,只不过它仅规定了畸变的绝对值的上限。
视场的整数编号可以是0,这说明使用最大的视场坐标,也可以是任何有效的视场编号。
注意,最大的畸变不一定总是在最大视场处产生。
得到的值总是以百分数为单位,以系统作为一个整体。
这个操作数对于非旋转对称系统可能无效。
AXCL(轴向色差):以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效.LACL(垂轴色差):这是定义的两种极端波长的主光线截点的y方向的距离。
对于非近轴系统无效TRAR(垂轴像差):在像面半径方向测定的相对于主光线的垂轴像差.TRAX(x方向垂轴像差):在像面x方向测定的相对于主光线的垂轴像差TRAY(Y方向垂轴像差):在像面Y方向测定的相对于主光线的垂轴像差TRAI(垂轴像差):在指定表面半口径方向测定的相对于主光线的垂轴像差.类似于TRAR,只不过是针对一个表面,而不是指定的像面.OPDC(光程差):指定波长的主光线的光程差.PETZ(匹兹伐曲率半径):以镜头长度单位表示,对非近轴系统无效PETC(匹兹伐曲率):以镜头长度单位的倒数表示,对非近轴系统无效RSCH:相对于主光线的RMS 斑点尺寸(光线像差)。
使用 ZEMAX®于设计、优化、公差和分析 摘要 光学设计软件 ZEMAX®的功能讨论可藉由使用 ZEMAX 去设计和分析一个投影系统 来讨论,包括使用透镜数组 (lenslet arrays) 来建构聚光镜 (condenser)。
简介 ZEMAX 以非序列性 (non-sequential) 分析工具来结合序列性 (sequential) 描光程序的传统功能, 且为一套能够研究所有表面的光学设计和分析的整合性软 件包,并具有研究成像和非成像系统中的杂散光 (stray light) 和鬼影 (ghosting) 的能力,从简单的绘图 (Layout)一直到优化和公差分析皆可达成。
根据过去的经验,对于光学系统的端对端 (end to end)分析往往是需要两 种不同的设计和分析工具。
一套序列性描光软件, 可用于设计、 优化和公差分析, 而一套非序列性或未受限制的 (unconstrained) 描光软件, 可用来分析杂散光、 鬼影和一般的非成像系统分析,包括照明系统。
序列性描光程序这个名词是与定义一个光学系统为一连串表面的工具有关。
所有的光线打到光学系统之后,会依序的从一个表面到另一个表面穿过这个系 统。
在定义的顺序上,所有的光线一定会交到所有的表面,否则光路将终止。
光 线不会跳过任何中间的表面;光线只能打在每一个已定义的表面一次。
若实际光 线路径交到一个表面上超过一次,如使用在二次描光 (double pass) 中的组件, 然后在序列性列表中,必须再定义超过一次的表面参数。
大部份成像光学系统,如照相机镜头、望远镜和显微镜,可在序列性模式中 完整定义。
对于这些系统,序列性描光具有许多优点:非常快、非常弹性和非常 普遍。
几乎任何形状的光学表面和材质特性皆可建构。
在成像系统中,序列性描 光最重要的优点为使用简单且高精确的方法来做优化和分析。
序列性描光的缺 点, 包括无法追迹所有可能的光路径 (即鬼影反射) 和许多无法以序列性方式来 描述的光学系统或组件。
【精品】ZEMAX评价函数1ZEMAX评价函数是指在ZEMAX光学设计软件中,用于计算光学系统性能参数的函数集合。
通过调用不同的函数,可以分析光学系统的成像、光损耗、像差以及色差等性能参数,从而优化设计。
1. 高效快速的性能参数计算在ZEMAX评价函数中,已经预先设置好了各种光学性能参数的计算公式,用户只需调用相应的函数,输入数据即可得到计算结果,无需自行编写性能参数计算公式,省去了大量时间和精力。
2. 可靠的结果验证ZEMAX评价函数的公式来源于国际通用的光学计算方法和经典的光学理论,因此计算结果具有高度准确性和可靠性。
3. 灵活的功能扩展ZEMAX评价函数可以根据用户需要进行功能扩展。
在ZEMAX软件中,用户可以自定义函数或修改已有函数的内容,实现更灵活的分析需求。
1. RMS (root mean square)RMS函数用于计算光学系统的像差根均方误差,是评价光学系统成像质量的重要指标。
它可以分别计算X、Y方向上的像差根均方值,也可以计算总像差根均方值。
计算结果越小,光学系统成像质量越好。
2. MTF (modulation transfer function)MTF函数用于计算光学系统的成像能力,它表示物体细节的成像程度。
MTF曲线的两个参数—— MTF50和MTF10 ——是表征光学系统成像能力的重要指标。
MTF50表示当空间频率为50lp/mm时MTF值下降到0.5时,对应的空间频率值为系统的分辨率。
MTF10表示当空间频率为10lp/mm时MTF值下降到0.1时,对应的空间频率值为系统的能够解析的小细节尺寸。
3. ENC (encircled energy)ENC函数用于计算光学系统的能量传输效率,它表示光束在光路中传输过程中,光强度随着传输距离而发生的变化。
ENC计算结果为一个函数,表示光束在不同位置上的能量分布情况。
4. Spot DiagramSpot Diagram函数用于生成光学系统的光斑图,它可以直观地反映光学系统的成像质量。
zemax主要优化函数表zemax主要优化函数表2009-11-17 15:05优化函数1、像差SPHA(球差):surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的球差贡献值,以波长表示。
如果表面编号值为零,则为整个系统的总和COMA(彗差) :surf表面编号/wave波长/target设定目标值/weight权重指定表面产生的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级彗差,对非近轴系统无效. ASTI(像散):指定表面产生像散的贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效FCUR(场曲):指定表面产生的场曲贡献值,以波长表示。
如果表面编号值为0,则是计算整个系统的场曲。
这是由塞得系数计算出的第三级场曲,对非近轴系统无效.DIST(畸变):指定表面产生的畸变贡献值,以波长表示。
如果表面编号值为0,则使用整个系统。
同样,如果表面编号值为0,则畸变以百分数形式给出。
这是由塞得系数计算出的第三级畸变,对与非近轴系统无效.DIMX(最大畸变值):它与DIST 相似,只不过它仅规定了畸变的绝对值的上限。
视场的整数编号可以是0,这说明使用最大的视场坐标,也可以是任何有效的视场编号。
注意,最大的畸变不一定总是在最大视场处产生。
得到的值总是以百分数为单位,以系统作为一个整体。
这个操作数对于非旋转对称系统可能无效。
AXCL(轴向色差):以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效.LACL(垂轴色差):这是定义的两种极端波长的主光线截点的y方向的距离。
对于非近轴系统无效TRAR(垂轴像差):在像面半径方向测定的相对于主光线的垂轴像差.TRAX(x方向垂轴像差):在像面x方向测定的相对于主光线的垂轴像差TRAY(Y方向垂轴像差):在像面Y方向测定的相对于主光线的垂轴像差TRAI(垂轴像差):在指定表面半口径方向测定的相对于主光线的垂轴像差.类似于TRAR,只不过是针对一个表面,而不是指定的像面.OPDC(光程差):指定波长的主光线的光程差.PETZ(匹兹伐曲率半径):以镜头长度单位表示,对非近轴系统无效PETC(匹兹伐曲率):以镜头长度单位的倒数表示,对非近轴系统无效RSCH:相对于主光线的RMS 斑点尺寸(光线像差)。
zemax_优化函数说明书优化操作数和数据域的用法名称说明Int1 Int2 Hxy,PxyABSO 绝对值操作数编号——ACOS 指定编号的操作数的值的反余弦值。
如果标记是0,则其单位为弧度,否则为度操作数编号标记—AMAG 角放大率。
这是像空间和物空间之间的近轴主光线角度的比值。
对于非近轴系统无效—波长—ANAR 在像面上测量的相对于主波长中主光线的角度差半径。
这个数定义成1-cosθ,这里θ是被追迹的光线与主光线之间的角度。
参见TRAR—波长—ASIN 指定编号的操作数的值的反正弦值。
如果标记为0,则其单位为弧度,否则为度操作数编号标记—ASTI 指定表面产生的像散贡献值,以波长表示。
如果表面编号值为0,则是针对整个系统。
这是由塞得和数计算得到的第三级色散,对非近轴系统无效表面波长—ATAN 指定编号的操作数的值的反正切值。
如果标记为0,则其单位为弧度,否则为度操作数标记—编号AXCL 以镜头长度单位为单位的轴向色差。
这是两种定义的最边缘的波长的理想焦面的间隔。
这个距离是沿着Z 轴测量的。
对非近轴系统无效———BLNK 不做任何事情。
用来将操作数列表的各个部分分隔开。
在操作数名称右边的空白处将随意地输入一注释行;这个注释行将在编辑界面和评价函数列表中同样显示———BSER 瞄准误差。
瞄准误差定义成被追迹的轴上视场的主光线的半坐标除以有效焦距。
这个定义将产生像的角度偏差的测量—波长—CMFV 结构评价函数值。
这个操作数调用了在两个用来定义一个光学虚拟全息系统的结构系统的任一个中定义的评价函数。
结构编号的值是1 或2,分别代表第一或第二结构系统。
操作数编号可以是0,这将从这个结构系统中获得整个评价函数的值,也可以是整数,这说明了从中记录数据值的操作数行号。
例如,假定结构编号是2,操作数编号是7,CMFV 将获得第2 个结构文件的评价函数中第7 个操作数的值。
如果在这个被优化的可逆系统中有一个以上的光学虚拟全息表面,结构编号可以加上2 来指代使用的第二个表面的参数,或者加上4 来指代使用的第三个表面的光学结构,等等。
各种光学自动软件最终都归结到优化函数结构和优化过程算法的问题。
最近,本人在使用ZEMAX过程中,仔细分析了一下构成ZEMAX软件的优化函数构成以及优化过程算法,有些心得,留给入门的朋友们共享。
一、 优化函数结构凡使用过SOD88软件(北京理工大学光电工程系开发)或者ZEMAX、CODEV的设计人员都知道,优化的参数包括以下几个种类:光学特性参数,例如焦距、入瞳距离、成像尺寸或者物高、物距,镜片间空气间距、镜片厚度等等;像质参数,例如畸变、场曲、彗差等等。
ZEMAX将所有这些要求达到的目标都作为一个优化元附加一定的权重系数组成一个优化函数,并且通过改变结构参数使得这个优化函数趋向最小。
数学表达式为:,其中 为各个优化元的权重系数, 为系统结构参数光学追迹出来的各个优化元,例如焦距、畸变、彗差等等, 为该优化元的目标值。
优化过程有局部优化和全局优化两种。
局部优化是指,通过改变系统结构参数的数值(半径、厚度、光学玻璃材料)计算出各个优化元的数值,然后构成整个优化函数的值的计算过程。
该过程的思路是解决当前状态已经处于“U”型中的某个位置,迫使其落到“U”中间的最小位置。
全局优化和局部优化不同的是,优化过程类似于一个搜索过程,这个搜索过程在结构参数限定的某个区域内进行优化,优化函数可能经历若干过波峰和波谷(多个极值之间)进行。
由于采用的方法不同,构成了多种全局优化算法。
全局优化能够避开某个局部极值寻找到更加优良的结构形式,使得光学设计距离完全自动化更进了一步。
当然,目前的各种算法都还有一定局限性,例如搜索能力强度、计算复杂程度,由此影响计算速度、计算资源需求量以及误差累计造成的准确度等等问题。
但是不管怎么样,现有的几种光学设计软件基于现有的高度发达计算机水平、光学设计发展水平和数学优化算法等,已经能够很好的满足具有一定光学设计经验知识的设计者们。
二、 ZEMAX的缺省优化函数结构入门的光学设计者通常知道在进行结构优化时选用default 缺省的优化函数,然后加入少量的优化目标例如焦距来进行优化分析,但是对于这个缺省结构怎么构成的常常缺乏深入分析,这在一定程度上限制了我们进一步充分利用软件优化能力的水平发挥。
实际上,缺省函数的构成结构并不复杂,它和ZEMAX提供给设计人员的“Default Merit Function(缺省优化函数)”紧密相关。
如下图所示。
第一行中的“Optimization Function and Reference (优化函数和参数方式)”。
他的主要思想是:从某个视场代表物点发出若干条光线,在像面上有一个分布形式,按照各个象差的定义进行象差数值计算。
第一个框中有“RMS(方均根)”和“PTV(峰谷差)”,第二个框中有差值计算的各种依据:WaveFront(波前)、Spot Radius(像点尺寸)、Spot X(X方向度量尺寸)、Spot Y(Y方向度量尺寸)、Spot X+Y(X和Y方向平均度量尺寸)。
第三个框中有“Cetriod(重 心点)”、“Chief Ray(主光线)”、“Mean(平均值)”。
举例说明各自配合的含义,缺省状况一般是:峰谷值+波前+质心点,优化的目标是:通过重心的光线到达像面时的相位和其他光线该相位状态时所在的位置有一个位置差别,将这些位置差别减小到最少,即认为各种像差都可能趋近于零。
从定义而言,这个组合适合于象差不是很大的场合,对于小象差系统其优化能力非常明显。
对于较大象差系统,采用“RMS + Spot Radius + Chief Ray”效果更为明显,后者以到达像面上的各条光线与主光线的差别来进行度量。
当然,这两种方法对于畸变的校正能力是有限的,因此对于畸变要求较高的系统需要加入畸变这个优化目标元进行优化校正。
那么,优化所使用的光线如何获得呢?其实这些光线的分布形式也是从缺省函数中定义的,如左图:软件提供了两种分布形式,一种是“高斯积分”形式:将轴对称的入瞳面分为数个环和扇面,每一个扇面中选择中心光线作为代表进行计算,每一个视场的所选用的光线数目都是两者的乘积;后一种模式是“矩阵模式”,它对于轴对称的入瞳按照正方形进行各种密度的抽样,一般而言,矩阵模式因为具有去渐晕的能力,在实际的设计中可能更为贴近实际效果。
不过由于设计人员的习惯性,一般采用传统的按照孔径直径进行选择的前种方法。
通常,光线的数量越多,抽样越密,计算得精确度越高,这主要取决于设计人员的实际系统和计算机资源。
以上的设置就构成了每一个视场对应点的优化结构,这些光线的具体分布与视场大小或者物面尺寸、入瞳直径或者相对孔径有关。
显然,每一条光线的优化目标都是和所选择的参考光线的差别为零,因此在优化函数列表中可以看到“target 值”都为零。
这样构成的结构在优化函数列表中占据了空间的绝大部分。
总数目 = 视场数目 * 光谱数目 * 每点抽样光线数目(例如Rings * Arms)。
除此之外,通常实际的设计过程中由于工程实践需要对镜片的厚度以及边缘厚度、空气间距进行设置,这也作为一个优化元进入了优化函数。
这就是MNCG、MNEA、MNEG、MXCG、MXCA等,他们限制了镜片和空气的厚度。
在设计人员没有进行自定义设置前,都可以在表格的空格处看到:缺省函数以及优化方式的说明。
三、 究竟哪些优化元需要自定义从上面的分析中已经知道,缺省的优化函数大体上解决了两个问题:第一个是光线的集中性,即通过各种优化模式使得物点发出的各条光线集中到像点上;第二个是工程问题,为了工程实现而限定镜片的厚度、空气厚度以及边缘厚度等,便于保证像质情况下留有固定镜片位置的余量。
由此可见光学性能参数大部分是没有作为优化目标元的。
例如:焦距、入瞳或出瞳距离、渐晕系数等等。
对于像质的目标,由于缺省情况下度量的角度不一样,设计者对某种象差严格有要求的具体设计系统,仍然需要自行设置。
因为缺省的光线评价计算出来的是一个总量,这个总量中各个像差的具体分布可能有很大的差别,例如场曲和彗差。
另外,对于畸变有严格要求的系统也需要进行限制。
当然,有一个问题就会出现,相互有关联的两个象差作为目标元自行设置之后,会出现一定的冲突,也就是说不一定优化效果很明显甚至于设计结构恶化。
这种情况下,需要设计人员干预进行。
常见的问题,例如目镜设计中对于彗差和畸变的校正,就容易出现反复的情况。
解决这个问题,不能单靠软件功能,而需要经验和一定的理论基础。
ZEMAX优化函数结构浅探许正光各种光学自动软件最终都归结到优化函数结构和优化过程算法的问题。
最近,本人在使用ZEMAX过程中,仔细分析了一下构成ZEMAX软件的优化函数构成以及优化过程算法,有些心得,留给入门的朋友们共享。
一、 优化函数结构凡使用过SOD88软件(北京理工大学光电工程系开发)或者ZEMAX、CODEV的设计人员都知道,优化的参数包括以下几个种类:光学特性参数,例如焦距、入瞳距离、成像尺寸或者物高、物距,镜片间空气间距、镜片厚度等等;像质参数,例如畸变、场曲、彗差等等。
ZEMAX将所有这些要求达到的目标都作为一个优化元附加一定的权重系数组成一个优化函数,并且通过改变结构参数使得这个优化函数趋向最小。
数学表达式为:,其中 为各个优化元的权重系数, 为系统结构参数光学追迹出来的各个优化元,例如焦距、畸变、彗差等等, 为该优化元的目标值。
优化过程有局部优化和全局优化两种。
局部优化是指,通过改变系统结构参数的数值(半径、厚度、光学玻璃材料)计算出各个优化元的数值,然后构成整个优化函数的值的计算过程。
该过程的思路是解决当前状态已经处于“U”型中的某个位置,迫使其落到“U”中间的最小位置。
全局优化和局部优化不同的是,优化过程类似于一个搜索过程,这个搜索过程在结构参数限定的某个区域内进行优化,优化函数可能经历若干过波峰和波谷(多个极值之间)进行。
由于采用的方法不同,构成了多种全局优化算法。
全局优化能够避开某个局部极值寻找到更加优良的结构形式,使得光学设计距离完全自动化更进了一步。
当然,目前的各种算法都还有一定局限性,例如搜索能力强度、计算复杂程度,由此影响计算速度、计算资源需求量以及误差累计造成的准确度等等问题。
但是不管怎么样,现有的几种光学设计软件基于现有的高度发达计算机水平、光学设计发展水平和数学优化算法等,已经能够很好的满足具有一定光学设计经验知识的设计者们。
二、 ZEMAX的缺省优化函数结构入门的光学设计者通常知道在进行结构优化时选用default缺省的优化函数,然后加入少量的优化目标例如焦距来进行优化分析,但是对于这个缺省结构怎么构成的常常缺乏深入分析,这在一定程度上限制了我们进一步充分利用软件优化能力的水平发挥。
实际上,缺省函数的构成结构并不复杂,它和ZEMAX提供给设计人员的“Default Merit Function(缺省优化函数)”紧密相关。
如下图所示。
第一行中的“Optimization Function and Reference (优化函数和参数方式)”。
他的主要思想是:从某个视场代表物点发出若干条光线,在像面上有一个分布形式,按照各个象差的定义进行象差数值计算。
第一个框中有“RMS(方均根)”和“PTV(峰谷差)”,第二个框中有差值计算的各种依据:WaveFront(波前)、Spot Radius(像点尺寸)、Spot X(X方向度量尺寸)、Spot Y(Y方向度量尺寸)、Spot X+Y(X 和Y方向平均度量尺寸)。
第三个框中有“Cetriod(重 心点)”、“Chief Ray(主光线)”、“Mean(平均值)”。
举例说明各自配合的含义,缺省状况一般是:峰谷值+波前+质心点,优化的目标是:通过重心的光线到达像面时的相位和其他光线该相位状态时所在的位置有一个位置差别,将这些位置差别减小到最少,即认为各种像差都可能趋近于零。
从定义而言,这个组合适合于象差不是很大的场合,对于小象差系统其优化能力非常明显。
对于较大象差系统,采用“RMS + Spot Radius + Chief Ray”效果更为明显,后者以到达像面上的各条光线与主光线的差别来进行度量。
当然,这两种方法对于畸变的校正能力是有限的,因此对于畸变要求较高的系统需要加入畸变这个优化目标元进行优化校正。
那么,优化所使用的光线如何获得呢?其实这些光线的分布形式也是从缺省函数中定义的,如左图:软件提供了两种分布形式,一种是“高斯积分”形式:将轴对称的入瞳面分为数个环和扇面,每一个扇面中选择中心光线作为代表进行计算,每一个视场的所选用的光线数目都是两者的乘积;后一种模式是“矩阵模式”,它对于轴对称的入瞳按照正方形进行各种密度的抽样,一般而言,矩阵模式因为具有去渐晕的能力,在实际的设计中可能更为贴近实际效果。