matlab第八章

例5.29 利用曲线对象绘制 y1 sin 和 y2 cos 并 利用文字对象完成标注。 theta=-pi:.1:pi; y1=sin(theta); y2=cos(theta); h=line(theta,y1,'LineStyle',':','Color','g'); line(theta,y2,'LineStyle','--','Color','b'); xlabel('-\pi \leq \theta \leq \pi') ylabel('sin(\theta)') title('Plot of sin(\theta)') text(-pi/4,sin(-pi/4),'\leftarrow sin(-\pi\div4)','FontSize',12) set(h,'Color','r','LineWidth',2) %改变曲线1的颜色和线宽
例5.30 利用曲面对象绘制三维曲面z=sin(y)cos(x)。
程序如下： x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x); axes('view',[-37.5,30]); hs=surface(x,y,z,'FaceColor','w','EdgeColor','flat'); grid on; xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis'); title('mesh-surf'); pause; set(hs,'FaceColor','flat');

WindowButtonDownFcn：当用户在图 形窗口内无控件的地方按下鼠标键时，调 用回调函数。 WindowButtonMotionFcn ： 当 用 户 在 图形窗口中移动鼠标时，调用回调函数。 WindowButtonUpFcn ： 当 用 户 在 图 形 窗口中释放鼠标键时，调用回调函数。
在模板设计界面中，可以选择创建新 的GUI或者打开原有的GUI。 在创建新的GUI时MATLAB提供以下4 种模板： 空白模板；
带有控制按钮模板；
带有坐标轴和菜单模板；
问答式对话框模板。
其中的空白模板如下图所示。
8.1.3 GUIDE提供的控件
在空白模板中，GUIDE提供界面控件 以及设计工具集来实现界面设计，其中， 控件分布在界面设计编辑器的左侧，如下 图所示。
3．对象浏览器
对象浏览器可以显示图形窗口中所有 对象的继承关系。
4．菜单编辑器
GUIDE能够创建菜单栏和上下文菜单。
当 选 择 【Tools】 菜 单 下 的 【Menu Editor】选项时即可打开下图所示的菜单 编辑器。
（1）菜单栏菜单 使用【New Menu】工具栏创建一个菜 单； 指定其隶属关系； 指定其属性。 下图显示一个设计的菜单，当激活图 形窗口时即可看到结果。
使用模态图形窗口使用户只能与当前执行 的GUI进行交互。
8.3 图形用户界面设计实例
编写函数，这些函数都包含在随图形 用户界面设计时产生的M文件中。 1．图形用户界面打开时自动运行的函数 simple_gui_OpeningFcn()，其具体代码 序列如下：
2．3个按钮的回调函数（Callback），其具 体代码序列如下：
询问用户并阻止MATLAB运行直至用户作 出回答，此时图形窗口仅可以被观察。 警告用户其指定的操作将会破坏文件的对 话框，该对话框能够执行用户所需的操作 前强迫用户作出回答。

第六章 matlab句柄绘图
——matlab语言的句柄绘图可以对 图形各基本对象进行更为细腻的 修饰，可以产生更为复杂的图形， 而且为动态图形的制作奠定了基 础。
整理课件
高层绘图与底层绘图的区别
高层绘图函数——是对整个图形进行操 作的，图形每一部分的属性都是按缺省 方式设置的，充分体现了matlab语言的 实用性。
整理课件
设置线条和窗口的颜色
set(h1,‘color’,[1 0 0])
RGB配色方案
set(h1,'color',[1 0.5 0])
10
10
9
9
8
8
7
7
6
6
5
整理课件
5
set(gcf,'color',[0.5 0.5 0.5]) set(gcf,'color',[0.5 0.6 0.8])
底层绘图函数——可以定制图形，对图 形的每一部分进行控制，用户可以用来 开发用户界面以及各专业的专用图形。 充分体现了matlab语言的开发性
整理课件
பைடு நூலகம்
例： t=0:pi/100:2*pi; y=sin(t); plot(t,y) %—— 自动出现一个窗口
整理课件
一、什么是句柄图形
句柄图形：利用底层绘图函数，通 过对对象属性的设置（Handle Graphics）与操作实现绘图。
整理课件
二、图形对象属性的获得与设置
句柄属性的设置与修改 get: 获得句柄图形对象的属性和返回某些
对象的句柄值 set: 改变图形对象的属性
整理课件
专用函数： gcf：当前窗口对象的句柄 Get Current

第8章MATLAB高级应用8.1 MATLAB应用接口MATLAB是一个看似封闭的系统，但具有多种接口功能，有外部数据接口和应用程序接口，用户可以十分方便地与其它应用程序交换数据和信息。

比如，MATLAB可以与C和FORTRAN程序相互调用，从而充分发挥MATLAB数值计算的长处，而避开其运行速度慢的短处。

8.1.1 MEX文件MEX就是MATLAB Executable的缩写，即MATLAB可执行程序。

MEX文件是由C 或FORTRAN程序编译生成的，也可以由M文件经由C源代码生成。

MEX文件在Windows 系统是扩展名为DLL的动态链接库，类似于MATLAB的内部函数，在M文件中可以直接调用。

MEX文件具有以下几个方面的应用：(1) 对于已存在的C或FORTRAN子程序，可以通过MEX文件在MATLAB环境中直接调用，而不必重新编写M文件。

(2) 由于MATLAB是解释性语言，运行如for等循环体时，会出现速度十分缓慢的现象，为了能提高速度，往往要使用MEX程序。

(3) 对于A/D、D/A卡，或其它PC硬件，可以直接用MEX文件进行访问。

(4) 利用MEX文件，可以使用如Windows用户图形界面等资源。

由于MATLAB是用C语言编写的，有很多科学计算子程序又来自FORTRAN程序库，因此在MATLAB中，通过调用用户自己开发的C或FORTRAN程序，由编译器编译成动态链接函数，执行速度和C或FORTRAN程序相同，就可以达到提高计算效率的目的。

在MATLAB中，如果有同名的文件则调用的顺序是先执行MEX文件，其次是DLL文件，最后才是M文件，而help命令则会只处理.m文件。

1. MEX文件系统设置MEX文件的编写与编译需要两个条件：已经安装的MATLAB应用程序组件及相应的工具和合适的C或Fortran语言编译器。

MATLAB本身包含了C语言编译器Lcc，但不包含Fortran编译器。

>> get(s1) num: {[0 0 3 4 5]} den: {[1 3 5 0 9]} Variable: 's' Ts: 0 ioDelay: 0 InputDelay: 0 OutputDelay: 0 InputName: {''} OutputName: {''} InputGroup: [1x1 struct] OutputGroup: [1x1 struct] Notes: {} UserData: []
>> s3=ss(s1) a= x1 x2 x3 x4 x1 -3 -1.25 0 -1.125 x2 4 0 0 0 x3 0 2 0 0 x4 0 0 1 0 b= u1 x1 1 x2 0 x3 0 x4 0 c= x1 x2 x3 x4 y1 0 0.75 0.5 0.625 d= u1 y1 0 Continuous-time model.
>> s4=ss(s2) a= x1 x2 x3 x4 x1 -1.891 1.737 -0.745 0 x2 -1.737 -1.891 -0.05194 0 x3 0 0 0.3913 2.201 x4 0 0 -0.5503 0.3913 b= u1 x1 0 x2 0 x3 0 x4 1.651 c= x1 x2 x3 x4 y1 2.714 0 0.8255 0 d= u1 y1 0 Continuous-time model.
使用时，只要输入环节的名称，不必输入其参 数矩阵。
控制系统工具箱LTI对象运算优先等级为 “状态空间>零极增益>传递函数”
实现的算法：以并联为例 算法：
f ( s) f A ( s) g B ( s) f B ( s) g A ( s) W ( s) g ( s) g A ( s) g B ( s)

X
[x,f,h]=fsolve(f,x0)返回一元或者多元函 数f在x0附近的一个零点，其中x0为迭代 初值，f返回f在x0的函数值，应该接近0； h返回值如果大于0，说明计算结果可靠， 否则计算结果不可靠。
例 求函数 y x sin(x2 x 1)在（-2，-0.1）内的零点
>>fun=inline(‘x*sin(x^2-x-1)’,’x’) >>fplot(fun,[-2,-0.1]);grid on >>x1=fzero(fun,[-1,-1.2]),x2=fzero(fun,[-1.2,-0.1]) 或x1=fzero(fun,-1.6),x2=fzero(fun,-0.6) 或[x1,f1,h1]=fsolve(fun,-1.6), [x2,f2,h2]=fsolve(fun,-0.6)
例：>> fzero('sin(x)',10)
>> fzero(@sin,10) >> fzero('x^3-3*x+1',1) >> fzero('x^3-3*x+1',[1,2]) >> fzero('x^3-3*x+1',[-2,0]) >> f=inline('x^3-3*x+1'); >> fzero(f,[-2,0]) >> fzero('x^3-3*x+1=0',1)
非线性方程的根
fzero 的另外一种调用方式
fzero(f,[a,b])
求方程 f=0 在 [a,b] 区间内的根。 方程在 [a,b] 内可能有多个根，但 fzero 只给出一个

【 例 8.1-1】 电 阻 电 路 如 图 8-1 所 示 ， 已 知 R1=R2=R3=1Ω ， R4=R5=R6=2Ω，uS1=4V，uS2=-2V，求I3。
电阻电路可用回路电流法、支路电流法、节 点电压法等方法求解，本例给出回路电流法。
【解】 解法一：回路电流法。回路电流法以回路电 流为变量，根据基尔霍夫电压定律（KVL）， 列写电路的独立回路组的KVL方程。如图81，将3个网孔作为选取的独立回路组，则回 路电流法的KVL方程组为



程序还调用 MATALB 信号处理工具箱中的周期 矩形脉冲的产生函数square。其调用格式为： square(T)；产生一个周期为2π的矩形脉冲函数。 其最大值为 1 ，最小值为 -1. 函数自变量取值为 相量T的各元素的值。 square (T, duty)；产生一个占空比duty、周期为 2π的矩形脉冲函数。 square(w*T, duty)；产生一个占空比duty、周期 为2π/w的矩形脉冲函数。 由以上说明可知，square(w*t, 50)产生一个周 期为 2π/w 、占空比为 50% 、幅值为± 1 的周期 性矩形脉冲。
������ ������������ ������������ //������������ Z 1
电流表的读数即为电流������的模值。
clear clc w=1000; ZR=20; Us=160; ZL=j*w*0.04 ZC=-j*(1/(w*20*1e-6)); Z1=(ZL*ZC)/(ZL+ZC); Z=ZR+Z1; U=Us*(Z1/Z); I=U/ZL; Iy=abs(I) 程序运行结果为 Iy = 3.9801
(R1+ R6+ R2) I1- R6 I3- R2 I2=- uS1 (R2+ R4 + R5) I2- R2 I1- R5 I3=- uS2 (R3+ R5+ R6) I3- R6 I1- R5 I2= uS2

基本图形的绘制 （3/3）
图形的其他操作
1. 图形保持 2. 图形子窗口 3. 坐标轴控制
2021年8月23日
第10页
MATLAB R2018b 基础教程
特殊图形的绘制（1/6）
条形图和面积图(Bar and Area Graphs)
MATLAB中主要有4个函数用于绘制条形图。 1. bar和barh 2. bar3，bar3h
图形的颜色是图形的一个重要因素，丰富的颜色 变化可以使图形更具有表现力。MATLAB中图形 的颜色控制主要由函数colormap完成。 MATLAB是采用颜色映射表来处理图形颜色的， 即RGB色系。
在二维等值线中添加高度值 绘制指定数据的二维等值线 绘制指定数据的三维等值线 绘制二维等值线，并用颜色填充各等值线之间的区域 用于计算等值线矩阵，通常由其他函数调用 绘制二维等值线对应的网格图 绘制二维等值线对应的表面图
2021年8月23日
第16页
MATLAB R2018b 基础教程
图形注释（1/2）
2021年8月23日
第11页
MATLAB R2018b 基础教程
特殊图形的绘制（2/6）
饼状图(Pie Charts) 饼状图是一种统计图形，用于显示每个元 素占总体的百分比，最常见的如磁盘容量 统计图。在MATLAB中，函数pie和pie3分 别用于绘制二维和三维饼状图。
2021年8月23日
第12页
添加基本注释
基本注释包括线头、箭头、文本框和用矩形或椭 圆圈画出重要区域。这些注释的添加可以通过图 形注释工具栏直接完成。
2021年8月23日
第17页
MATLAB R2018b 基础教程
图形注释（2/2）
添加其他注释

第8章MATLAB方程数值求解例8-1用直接解法求解下列线性方程组。

程序如下：A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b例8-2用LU分解求解例8-1中的线性方程组。

程序如下：A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';[L,U]=lu(A);x=U\(L\b)例8-3 用QR分解求解例8-1中的线性方程组。

程序如下：A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';[Q,R]=qr(A);x=R\(Q\b)例8-4 用Cholesky分解求解例8-1中的线性方程组。

命令如下：>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >> b=[13,-9,6,0]';>> R=chol(A)Jacobi迭代法的MA TLAB函数文件jacobi.m如下：function [y,n]=jacobi(A,b,x0,ep)if nargin==3ep=1.0e-6;elseif nargin<3errorreturnendD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B=D\(L+U);f=D\b;y=B*x0+f;n=1; %迭代次数while norm(y-x0)>=epx0=y;y=B*x0+f;n=n+1;end例8-5 用Jacobi迭代法求解下列线性方程组。

设迭代初值为0，迭代精度为10-6。

在程序中调用函数文件jacobi.m，程序如下：A=[10,-1,0;-1,10,-2;0,-2,10];b=[9,7,6]';[x,n]=jacobi(A,b,[0,0,0]',1.0e-6)Gauss-Serdel迭代法的MA TLAB函数文件gauseidel.m如下：function [y,n]=gauseidel(A,b,x0,ep)if nargin==3ep=1.0e-6;elseif nargin<3errorreturnendD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1; %迭代次数while norm(y-x0)>=epx0=y;y=G*x0+f;n=n+1;end例8-6 用Gauss-Serdel迭代法求解例8-5中的线性方程组。

end
ห้องสมุดไป่ตู้end
第8章 MATLAB综合实训
subplot(122)
imshow(uint8(D))
%uint8(D)强制转
换D的数据格式
title('置乱后的图像')
imwrite(uint8(D),'d:\image.bmp','bmp') %
保存置乱后的图像
fid=fopen('d:\test.bin','wb')
C=zeros(65536,1);
for i=1:65536 C(i)=A(B(i));
%置乱，用密钥重新排列 图像矩阵
end
第8章 MATLAB综合实训
D=zeros(256);
k=1;
for i=1:256
%将单列矩阵转换成与原
图像同样尺寸的矩阵
for j=1:256
D(j,i)=C(k);
k=k+1;
讲解演示，评估项目的完成情况，评价内容如 下： 1）图像的视觉效果； 2）处理图像与原始图像之间的偏离程度； 3）图形用户界面是否友好。
第8章 MATLAB综合实训
8.2 数字图像增强
图像增强就是对图像进行加工，以得到对 具体应用来说视觉效果更“好”，更“有用” 的图像。 一、 项目说明
1．项目要求 （1）图像测试 （2）图像添加噪声
%读入密钥
RB=fread(fid,65536,'double');
fclose(fid)
第8章 MATLAB综合实训
RC=RD(:); RA=zeros(65536,1); for i=1:65536

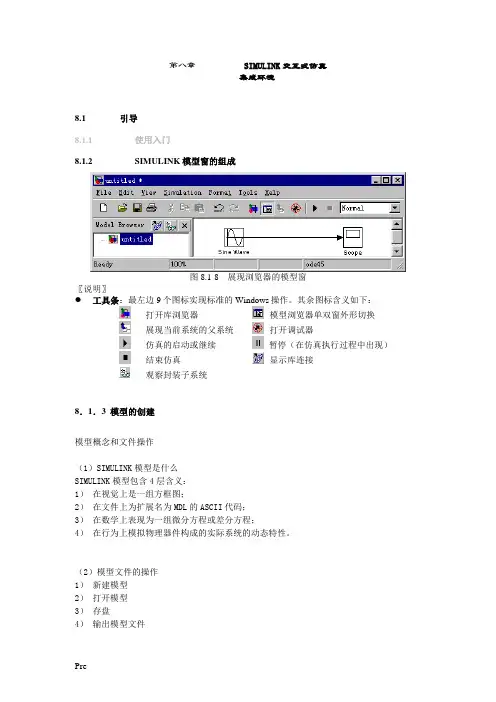
第八章SIMULINK交互式仿真集成环境8.1引导8.1.1使用入门8.1.2SIMULINK模型窗的组成图8.1-8 展现浏览器的模型窗〖说明〗工具条：最左边9个图标实现标准的Windows操作。

其余图标含义如下：打开库浏览器模型浏览器单双窗外形切换展现当前系统的父系统打开调试器仿真的启动或继续暂停（在仿真执行过程中出现）结束仿真显示库连接观察封装子系统8．1．3 模型的创建模型概念和文件操作（1）SIMULINK模型是什么SIMULINK模型包含4层含义：1）在视觉上是一组方框图；2）在文件上为扩展名为MDL的ASCII代码；3）在数学上表现为一组微分方程或差分方程；4）在行为上模拟物理器件构成的实际系统的动态特性。

（2）模型文件的操作1）新建模型2）打开模型3）存盘4）输出模型文件（3）模块操作（4）信号线操作（5）产生连线（6）信号线的分支和折曲（7）插入模块（8）信号线标识（label ）（9）对模型的注释8．2 常用的Sourse 库信号源【例8.2-1】如何调用MATLAB 工作空间中的信号矩阵作为模型输入。

本例所需的输入为⎪⎩⎪⎨⎧<≤<≤-=elseT t T T t t T t t u 200)2()(22。

（1）编写一个产生信号矩阵的M 函数文件function TU=source82_1(T0,N0,K) t=linspace(0,K*T0,K*N0+1);% t=linespace(a,b,n) 等于 t=a:( b-a)/( n-1): b N=length(t);u1=t(1:(N0+1)).^2;u2=(t((N0+2):(2*N0+1))-2*T0).^2; u3(1:(N-(2*N0+2)+1))=0; u=[u1,u2,u3]; TU=[t',u'];（2）构造简单的接收信号用的实验模型图8.2-8 接收信号用的实验模型（3）模块的参数设置（4）在指令窗中，运行以下指令，在MATLAB 工作空间中产生TU 信号矩阵。

虽然句柄变量可以取任意名字，但为了提高可读性， 句柄对象的变量取名一般以大写的H开头，跟之以一个辨 识对象类型的字母，然后是一个下划线，最后是一个或几 个描述符。例如，Hf_fig是一个图形窗口的句柄，Ha_ax1 是坐标轴对象的句柄，而Ht_title是一个文本对象的句柄。 当对象类型不知道时，用字母x，如Hx_obj。 图形函数都为所建立的每个对象返回一个句柄（或句 柄的列向量）。包括plot，mesh，surf等。有一些图形由 一个以上对象组成。一个网格图由一个曲面组成，它只有 一个句柄；而waterfall图形由许多线条对象组成，每个 线条对象都有各自的句柄。 例如，» Hl_wfall=waterfall(peaks(20)) 对线条返 回一个包含着20个句柄的列向量
每次创建一个对象时，就为它建立一个唯一的句柄。计 算机屏幕作为根对象常常是0。 » Hf_fig=figure命令建立一个新的图形窗口，变量 Hf_fig中返回它的句柄值。图形窗口的句柄为整数，通常 显示在图形窗口标题条中。其它对象句柄是MATLAB双精度 的浮点值。 可以获得图形、坐标轴和其它对象的句柄。 例如，» Hf_fig=gcf返回当前图形窗口的句柄值，而 Ha_ax=gca返回当前图形窗口内当前坐标轴的句柄值。
函数set改变句柄图形对象属性，使用语法为： set(handle,‘PropertyName’,value) 例如： » set(Hf_1,‘Position’,p_vect) %将具有句柄 Hf_1的图形位臵设为向量p_vect所指定的值 » set(Hl_a,‘color’,‘r’) %将具有句柄 Hl_a的对象的颜色设臵成红色 一般情况下，函数set可以有任意数目的 (‘PropertyName’,PropertyValue)对。 例如： » set(Hl_a,‘Color’,‘r’,‘Linewidth’,2,‘LinStyle’,‘ --’ ） %将具有句柄Hl_a的线条变成红色，线宽为 2点，线型为破折号

MATLAB教程第8章MATLAB数值积分与微分1.数值积分数值积分是计算函数的定积分值的近似方法。

在MATLAB中，有几个函数可以帮助我们进行数值积分。

(1) quad函数quad函数是MATLAB中用于计算一维定积分的常用函数。

它的语法如下：I = quad(fun, a, b)其中，fun是被积函数的句柄，a和b分别是积分区间的下界和上界，I是近似的积分值。

例如，我们可以计算函数y=x^2在区间[0,1]内的积分值：a=0;b=1;I = quad(fun, a, b);disp(I);(2) integral函数integral函数是在MATLAB R2024a版本引入的新函数，它提供了比quad函数更稳定和准确的积分计算。

integral函数的语法如下：I = integral(fun, a, b)其中fun、a和b的含义与quad函数相同。

例如，我们可以使用integral函数计算函数y = x^2在区间[0, 1]内的积分值：a=0;b=1;I = integral(fun, a, b);disp(I);2.数值微分数值微分是计算函数导数的近似方法。

在MATLAB中，可以使用diff 函数计算函数的导数。

(1) diff函数diff函数用于计算函数的导数。

它的语法如下：derivative = diff(fun, x)其中，fun是需要计算导数的函数，x是自变量。

例如，我们可以计算函数y=x^2的导数：syms x;fun = x^2;derivative = diff(fun, x);disp(derivative);(2) gradient函数gradient函数可以计算多变量函数的梯度。

它的语法如下：[g1, g2, ..., gn] = gradient(fun, x1, x2, ..., xn)其中fun是需要计算梯度的函数，x1, x2, ..., xn是自变量。

例如，我们可以计算函数f=x^2+y^2的梯度：syms x y;fun = x^2 + y^2;[gx, gy] = gradient(fun, x, y);disp(gx);disp(gy);以上是MATLAB中进行数值积分和微分的基本方法和函数。

>>A(:,[1,3]) %按照顺序访问矩阵A的第一列和第三列 ans = 1 1 3 3 7 9 >>A(:,[3,1]) %按照顺序访问矩阵A的第三列和第一列 ans = 1 1 3 3 9 7
(2)、在原矩阵的基础上增加或删除一行或一列
例如，>>A=[1 2 1 5;3 3 3 6;7 8 9 10] A=1 2 1 5 3 3 3 6 7 8 9 10 >>A=[A;[1 2 3 4]] %在A中加入第四行（注意分号的用法） A=1 2 1 5 3 3 3 6 7 8 9 10 1 2 3 4 >>A=[A,[2 3 4 1]’] %在A中加入第五列（注意逗号的用法） A =1 2 1 5 2 3 3 3 6 3 7 8 9 10 4 1 2 3 4 1
第8章 MATLAB基本操作知识
一、 基础知识
二、 矩阵运算
三、求解线形方程组
四、 多项式运算
二、矩阵运算
1、矩阵的创建
（1）矩阵的创建 通常矩阵与数组的意义相同，都是指含有m行n列数字的矩 形结构。要用MATLAB来做矩阵运算，首先要将矩阵输入到 MATLAB中。下面就将介绍矩阵的输入方法。 例如，矩阵
>>A(:,2)=[ ] %删除矩阵Ａ的第二列 A= 1 1 5 2 3 3 6 3 7 9 10 4 1 3 4 1 >>A(2,:)=[ ] %删除矩阵Ａ的第二行 A= 1 1 5 2 7 9 10 4 1 3 4 1 >>A([2:3],[1,3:4]) %访问矩阵Ａ的第2，3行和第1，3，4列 A= 7 10 4 1 4 1
（3）特殊矩阵 zeros(m,n) ones(m,n) eye(n) magic(n) diag(x) hilb(n) vander(x)

数学软件
河北理工大学理学院 阎少宏
1 shaohong@
第一章
1
第八章
SIMULINK交互式仿真集成环境 交互式仿真集成环境
SIMULINK是MATLAB最重要的组件之一，它提供了实现动态 是 最重要的组件之一， 最重要的组件之一 系统建模、 仿真的—个集成环境 它的存在使MATLAB的功能得 个集成环境。 系统建模 、 仿真的 个集成环境 。 它的存在使 的功能得 到进一步扩展。在该环境中，无须书写大量的程序． 到进一步扩展。在该环境中，无须书写大量的程序．而只要通过简 单直观的鼠标操作，就可构造出复杂的仿真模型。 单直观的鼠标操作，就可构造出复杂的仿真模型。
SIMULINK模型的三种组件： 模型的三种组件： 模型的三种组件 信源 系统 信宿
视觉上： 视觉上：方框图 文件上：扩展名为 文件上：扩展名为MDL的ASCⅡ代码 的 Ⅱ 数学上： 数学上：一组微分方程或差分方程 行为上： 行为上：实际系统的动态性状
第一章
7
二 模型文件的操作 主要操作：新建、打开、存盘、 主要操作：新建、打开、存盘、打印
第一章
4
图标或命令方式） 一、启动SIMULINK模块库窗口 （图标或命令方式） 启动 模块库窗口 二、打开source子库 打开 子库
三、打开空白模型窗口 四、在空白窗口中添加所需source模块（如：正弦波模块 模块（ 在空白窗口中添加所需 模块 Sine Wave） ） 模块（ 示波器Scope） 五、添加信宿库Sinks模块（如：示波器 添加信宿库 模块 ） 六、连接信号线 至此一简单模型已经建成
第一章
18
●磁滞回环模块(Backlash)，和其在控制系统中的定义一致。 磁滞回环模块 ，和其在控制系统中的定义一致。 在此模块组中定义了很多分段线性的静态非线性模块， 在此模块组中定义了很多分段线性的静态非线性模块，如死区非 线性(Dead zone)、 饱和非线性 线性 、 饱和非线性(Saturation)、量化模块 、 (Quantizer)、继电模块 、继电模块(Relay)、变化率限幅模块 (Rate Limiter) 、 其实其中很多模块可以由一维查表模块实现。 等，其实其中很多模块可以由一维查表模块实现。

end end TU=[t',u']; % t,u必须转换成列向量形式
▪ 构造一个简单的显示信号的实验模型
▪ 设置模块参数，双击模块From Workspace， 弹出参数设置对话框，在“Data”栏中填写 TU，按下“OK”键，保存参数设置 。
▪ 运行M文件
▪ 启动模型仿真 ，双击示波器Scope模块 ； 观察仿真结果
功能
说明
Integrator
积分环节
该模块将输入端信号经过数值积分，在输出端直接输出积 分后的信号
Derivative
微分环节
该模块将输入端信号经过一阶数值微分，在输出端直接输 出微分后的信号
Zero-Pole State-Space
零极点模型 状态方程
该模块采用零－极点形式定义传递函数 该模块采用状态方程的形式对线性系统进行时域描述
MATLAB 2013
第8章 Simulink 仿真设计
2014.1.12
内 容：
➢ Simulink操作入门 ➢ Simulink模型的创建 ➢ Simulink模块库简介 ➢ 子系统及其封装技术 ➢ S函数模块应用 ➢ 综合应用
8.1 Simulink入门
认识仿真：
以一个简单的实例为大家演示 Simulink的建模及仿真过程
跟我练：
方法一、采用MATLAB函数模块构建 建立一个函数式M文件，保存为f808.m
function y=f808(t) y=7*t*t+12;
▪ 启动Simulink打开一个名为untitled的模型编辑窗 口，将所需模块添加到模型中。从Sources模块库 中拖入Clock（时钟）模块，从User-Defined Function（用户自定义函数）模块库中拖入 MATLAB Fcn模块，从Sinks模块库中拖入To Workspace、Scope等模块，并进行连接。