当前位置：文档之家 › matlab习题第八章

matlab习题第八章

  • 格式：doc
  • 大小：52.00 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

第8章MATLAB图形用户界面设计

第8章MATLAB图形用户界面设计

例5.29 利用曲线对象绘制 y1 sin 和 y2 cos 并 利用文字对象完成标注。 theta=-pi:.1:pi; y1=sin(theta); y2=cos(theta); h=line(theta,y1,'LineStyle',':','Color','g'); line(theta,y2,'LineStyle','--','Color','b'); xlabel('-\pi \leq \theta \leq \pi') ylabel('sin(\theta)') title('Plot of sin(\theta)') text(-pi/4,sin(-pi/4),'\leftarrow sin(-\pi\div4)','FontSize',12) set(h,'Color','r','LineWidth',2) %改变曲线1的颜色和线宽
例5.30 利用曲面对象绘制三维曲面z=sin(y)cos(x)。
程序如下： x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x); axes('view',[-37.5,30]); hs=surface(x,y,z,'FaceColor','w','EdgeColor','flat'); grid on; xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis'); title('mesh-surf'); pause; set(hs,'FaceColor','flat');

第八章 基于MATLAB的科学计算—常微分方程数值解法

第八章 基于MATLAB的科学计算—常微分方程数值解法

科学计算—理论、方法及其基于MATLAB 的程序实现与分析微分方程（组）数值解法§1 常微分方程初值问题的数值解法微分方程（组）是科学研究和工程应用中最常用的数学模型之一。

如揭示质点运动规律的Newton 第二定律：()()()⎪⎩⎪⎨⎧'='==000022x t x x t x t F dt xd m （１） 和刻画回路电流或电压变化规律的基尔霍夫回路定律等，但是，只有一些简单的和特殊的常微分方程及常微分方程组，可以求得用公式给出的所谓“解析解”或“公式解”，如一阶线性微分方程的初值问题：()()00y y t f ay dtdy=+= （２） 的解为：()()()τττd f e y e t y tt a at ⎰-+=00 （３）但是，绝大多数在实际中遇到的常微分方程和常微分方程组得不到“解析解”，因此，基于如下的事实：１、绝大多数的常微分方程和常微分方程组得不到（有限形式的）解析解；２、实际应用中往往只需要知道常微分方程（组）的解在（人们所关心的）某些点处的函数值（可以是满足一定精度要求的近似值）；如果只需要常微分方程（组）的解在某些点处的函数值，则没有必要非得通过求得公式解，然后再计算出函数值不可，事实上，我们可以采用下面将介绍的常微分方程（组）的初值问题的数值解法，就可以达到这一目的。

一般的一阶常微分方程（组）的初值问题是指如下的一阶常微分方程（组）的定解问题：()()000,y t y t t t y t F dtdyf=≤≤= （７）其中()()()()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=t y t y t y t y n 21 （８）()()()()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=y t f y t f y t f y t F n ,,,,21 （９）常微分方程（组）的初值问题通常是对一动态过程（动态系统、动力系统）演化规律的描述，求解常微分方程（组）的初值问题就是要了解和掌握动态过程演化规律。

数字信号处理及MATLAB实现第八章习题答案

数字信号处理及MATLAB实现第八章习题答案

1. 数字信号处理器有哪些结构特点？答：1. DSP内部采用的是程序空间和数据空间分开的哈佛结构；2. 多总线结构；3. 流水线结构：在DSP中，执行一条指令，需要通过取指、译码、取操作数和执行四个阶段。

在程序运行过程中，这四个阶段不是依次进行的，而是重叠的进行的；4. 多处理单元：DSP内部通常包括有算术逻辑运算单元(ALU)、辅助寄存器运算单元(ARAU)、累加器(ACC)以及硬件乘法器(MUL)等多个处理单元。

它们可以在一个指令周期内同时进行运算；5. 硬件配置强：新一代DSP的接口功能愈来愈强，如：TMS320C5000系列芯片片内具有串行口、主机接口(HPl)、DMA控制器、软件控制的等待状态产生器、锁相环时钟产生器以及实现在片仿真符合IEEEll49．1．标准的测试访问口，更易于完成系统设计。

许多DSP芯片都可以工作在省电方式，使系统功耗降低。

2. TMS320C54x系列DSP片内有多少条总线，具体说明有哪些？答：TMS320C54x系列DSP是TI公司于1996年推出的新一代定点数字信号处理器。

其采用先进的修正哈佛结构，片内有8条总线，分别为1条程序存储器总线，3条数据存储器总线和4条地址总线。

3. TMS320VC5402的在片外围电路有哪些？答：1. 软件可编程等待状态发生器；2. 可编程分区转换逻辑电路；3.带有内部振荡器或用外部时钟源的片内锁相环(PLL)时钟发生器；4. 时分多路(TDM)串行口；5. 缓冲串行口(BSP)；6. 2个16位定时器；7. 8位并行主机接口(HPl)；8. 外部总线关断控制，以断开外部的数据总线、地址总线和控制信号。

4. TMS320VC5402有哪些片内资源？答：TMS320VC5402的片内资源按功能包括运算单元、寄存器、片内RAM 和ROM、片外存储器接口、DMA控制器、主机接口、串口、定时器、时钟产生器和中断控制器。

5. CCS有几种工作模式？具体说明。

matalb第八章课后习题

matalb第八章课后习题

Matlab第八章部分习题1. 以下是100 次刀具故障记录，即故障出现时该刀具完成的零件数。

分析这批数据是否服从正态分布，并求其均值和均方差。

注意，由于纪录失误，其中可能有些数据是错误的,要对此进行适当处理。

459, 362, 624, 542, 509, 584, 433, 748, 815, 505, 612, 452, 434, 982,640782, 742, 565, 706, 593, 680, 926, 653, 164, 487, 734, 608, 428, 1153, 593, 844, 527, 552, 513, 781, 474, 388, 824, 538, 862, 659, 775, 859, 755, 649, 697, 515, 628, 954, 771, 609, 2, 960, 885, 610, 292, 837, 473, 677, 358, 638, 699, 634, 555, 570, 84, 416, 606, 1062, 484, 120, 447, 654, 564, 339, 280, 246, 687, 539, 790, 581, 621, 724, 531, 512, 577, 496, 468, 499, 544, 645, 764, 558, 378, 765, 666, 763, 217, 715, 310, 851x1=[459 362 624 542 509 584 433 748 815 505 ]x2=[612 452 434 982 640 742 565 706 593 680 ]x3=[926 653 164 487 734 608 428 1153 593 844 ]x4=[527 552 513 781 474 388 824 538 862 659 ]x5=[775 859 755 649 697 515 628 954 771 609 ]x6=[402 960 885 610 292 837 473 677 358 638 ]x7=[699 634 555 570 84 416 606 1062 484 120 ]x8=[447 654 564 339 280 246 687 539 790 581 ]x9=[621 724 531 512 577 496 468 499 544 645 ]x10=[764 558 378 765 666 763 217 715 310 851 ]x=[x1 x2 x3 x4 x5 x6 x7 x8 x9 x10]; [mean(x),var(x)]ans =1.0e+004 *0.0600 3.86632. 表8.4给出了1930年各国人均年消耗的烟去数以及1950年男子死于肺癌的死亡率。

MATLAB基础及应用(第4版)8

MATLAB基础及应用(第4版)8
（1）图像测试 先将教师提供的图像读入工作空间，记下图像尺寸和 数据类型，利用hist函数绘制概率分布图，注意横坐标 的数值范围和步长；使用统计函数mean计算图像均值。
（2）图像添加噪声 噪声信号可以由随机矩阵函数实现，直接与图像相加 即可，注意相加后的值不要超过图像的数据范围，也 不要小于0；如果加噪的效果不明显，可增大随机矩阵 的元素数值，例如乘以一个大于1的系数。
1）图像的视觉效果； 2）处理图像与原始图像之间的偏离程度； 3）图形用户界面是否友好。
8.2 数字图像增强
图像增强就是对图像进行加工，以得到对具体 应用来说视觉效果更“好”，更“有用”的图 像。 一、 项目说明 1．项目要求 （1）图像测试 （2）图像添加噪声
（3）图像的对比度调整 （4）图像求反 （5）图像平滑 （6）拓展要求
实现图像增强操作的图形用户界面设计，包括 “图像测试”、“添加噪声”、“对比度调整”、 “图像求反”和“图像平滑”等基本功能。
2．实施步骤 1）讨论、研究项目要求，明确项目内容； 2）学习项目设计提示，分析算法； 3）仿真算法，完成项目； 4）项目演示、讲解设计方案，完成项目评价
二、项目设计提示
二、项目设计提示
函数功能 装入图像 读入图像 图像显示 图像剪裁
图像大小调 整
图像旋转
图像插值
函数格式
说明
load 文件名
将以mat为扩展名的图像文件直接装入工作空间，赋值给变量 X，数据类型为double
A=imread（‘文件名’，‘图像格式’) A=imread（‘文件名.扩展名’)
从图像文件中读入图像数据到变量A 中。图像格式包括bmp、 tif、jpg、png等
变量名=imresize（图像变量名，调整系数， 比例调整。调整系数为“放大”或“缩小”的倍数；参数表

matlab1-8章课后作业

matlab1-8章课后作业

MATLAB基础教程 1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件，是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境，已被广泛应用于不同领域。

Matlab的基本功能包括：数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink 建模仿真功能、自动代码生成功能。

Matlab第二章1．创建double的变量，并进行计算。

(1) a=87，b=190，计算 a+b、a-b、a*b。

(2)创建 uint8 类型的变量，数值与(1)中相同，进行相同的计算。

>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2，v=3，计算：(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u)ans =15.4189>> sqrt(u-3*v)/(u*v)ans =0 + 0.4410i4.计算如下表达式：(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。

第8章 MATLAB方程数值求解_习题答案

第8章 MATLAB方程数值求解习题8一、选择题1．下列方法中与线性方程组求解无关的是（）。

CA．左除B．矩阵求逆C．矩阵转置D．矩阵分解2．对于系数矩阵A的阶数很大，且零元素较多的大型稀疏矩阵线性方程组，非常适合采用（）求解。

BA．直接法B．迭代法C．矩阵求逆D．左除3．已知函数文件fx.m：function f=fx(x)f=2*x.^2+5*x-1;则求f(x)=2x2+5x-1=0在x0=-2附近根的命令是（）。

DA．z=fzero(fx,0.5) B．z=fzero(@fx,0.5)C．z=fzero(fx,-2); D．z=fzero(@fx,-2);4．已知：fx=@(x) 2*x.^2+5*x-1;则求f(x)=2x2+5x-1=0在x0=-2附近根的命令是（）。

CA．z=fzero(fx,0.5) B．z=fzero(@fx,0.5)C．z=fzero(fx,-2); D．z=fzero(@fx,-2);5．下列选项中不能用于求常微分方程数值解的函数是（）。

AA．ode10 B．ode23 C．ode45 D．ode113二、填空题1．线性方程组的求解方法可以分为两类，一类是，另一类是。

前者是在没有舍入误差的情况下，通过有限步的初等运算来求得方程组的解；后者是先给定一个解的，然后按照一定的算法不断用变量的旧值递推出新的值。

直接法，迭代法，初始值2．MA TLAB用函数来求单变量非线性方程的根。

对于非线性方程组，则用函数求其数值解。

fzero，fsolve3．用数值方法求解常微分方程的初值问题，一般都是用系列函数，包括ode23、ode45等函数，各有不同的适用场合。

ode4．ode23、ode45等函数是针对一阶常微分方程组的，对于高阶常微分方程，需先将它转化为一阶常微分方程组，即。

状态方程三、应用题21．分别用矩阵除法以及矩阵分解求线性方程组的解。

⎪⎩⎪⎨⎧=+-=++=++57347310532)1(z y x z y x z y x 123134124345132(2)53241x x x x x x x x x x x +-=⎧⎪+-=⎪⎨--+=⎪⎪+=-⎩(1): 矩阵除法:A=[2,3,5;3,7,4;1,-7,1]; B=[10,3,5];%B 是行向量 x=A\B'%将B 变成列向量 矩阵分解:A=[2,3,5;3,7,4;1,-7,1]; B=[10,3,5];%B 是行向量 [L,U]=lu(A); x=U\(L\B') (2):和上面的程序一样。

第8章 积分的MATLAB求解


无穷限的反常积分

对于无穷区间上的反常积分通常有两种解决方法，下面分别介绍： 无穷区间逼近 为叙述方便，仅考虑积分 的求解，由于
因此，取
且
，有
上式中的每个积分都是正常积分，利用前面介绍的方法求解。当
时停止计算。

变量替换
在某些情况下，可以通过变量替换将无穷区间的积分变成有限区间的积分。例如，用 变量替换
1.不定积分的定义
如果在区间 上，可导函数
称为被积函数，
称为被积表达式， 称为积分变量，也
。
2.不定积分的几何意义
函数 的一个原函数 的图像称为 的一条积分曲线。对于任意常数 ， 表示的是一族曲线，我们称这个曲线族为 的积分曲线族。因此， 在几何上表示的是 的积分曲线族，而 正是积分曲线的斜率。积分曲线族中的每一条曲线在对应于同一横 坐标 处的切线都有相同的斜率 ，所以在这些点处，它们的切线相互平行，并且任意 两条积分曲线的纵坐标之间相差一个常数。因此，积分曲线族中的每一条曲线都可以由曲线 沿 轴上下移动而得到，如图所示。
1.无穷限的反常积分
这时也称反常积分 收敛；如果上述极限不存在，则函数 就没有意义，习惯上称为反常积分 发散，这时记号 类似地，设函数 在无穷区间 在区间 上连续，取 上的反常积分，记作 ，如果极限 ，即
在区间 上的反常积分 不再表示数值。 存在，则称此极限为函
数
这时也称反常积分 设函数 在区间
收敛；如果上述极限不存在，则称反常积分 发散。 上连续，如果反常积分 和 都收敛，则称上述两反常积分之和为函数 在无穷区间 上的反常积分，记作
这时也称反常积分 类似地，设函数 存在，则定义
收敛，如果上述极限不存在，则称反常积分 发散。 在 上连续，点 为函数 的瑕点，取 ，如果极限

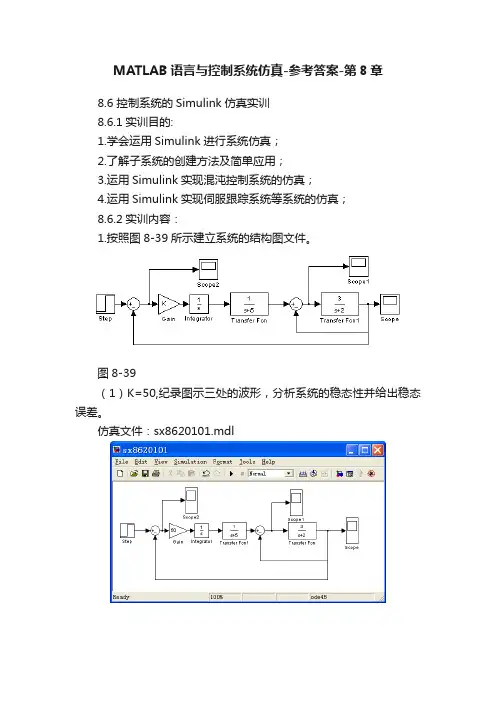
MATLAB语言与控制系统仿真-参考答案-第8章

MATLAB语言与控制系统仿真-参考答案-第8章8.6 控制系统的Simulink仿真实训8.6.1实训目的:1.学会运用Simulink进行系统仿真；2.了解子系统的创建方法及简单应用；3.运用Simulink实现混沌控制系统的仿真；4.运用Simulink实现伺服跟踪系统等系统的仿真；8.6.2实训内容：1.按照图8-39所示建立系统的结构图文件。

图8-39（1）K=50,纪录图示三处的波形，分析系统的稳态性并给出稳态误差。

仿真文件：sx8620101.mdl系统稳定，稳态误差为0；（2）K=200,纪录图示三处的波形，根据曲线分析系统的稳定性。

仿真文件：sx8620102.mdl由输出曲线可以看出闭环系统不稳定；（3）编写程序求取K=200时的闭环传递函数，求出系统的闭环极点（特征根），说明系统的稳定性，分析与（2）得出的结论是否一致。

%实训8620103.mn1=3;d1=[1,2];[n2,d2]=cloop(n1,d1);sysa=tf(n2,d2);sysb=tf([200],[1,0])*tf([1],[1,5]);sysc=sysa*sysb/(1+sysa*sysb);[nc,dc]=tfdata(sysc,'v');roots(dc)>> ans =-12.0549 1.0275 + 6.9797i 1.0275 - 6.9797i -5.0000 + 0.0000i -5.0000 - 0.0000i有两个特征根在右半平面，闭环系统不稳定；与（2）得出的稳定性结论一致。

2. 子系统创建实验（1）建立如下系统。

（2）选定范围,创建子系统并定义变量a 。

图8-40(3)利用创建的子系统,分别记录10,8,6,4,2 a 时所示系统的输出波形。

a=2a=4a=6a=8a=103.已知四维混沌系统的运动方程如下，试用Simulink 进行仿真。

+-=+-=-+=+-=321444213343121243212110)(10)(35x x x x xx x x x x x x x x x xx x x x x x （1）四个积分器的初始值自定，建议在（0.01，3.0）范围内随机给出。

MATLAB第1-8章答案

第1章一、思考题4. （1） B=A(2:5,1:2:5)（2）A(7)=[]（3） A=A+30（4）size(A)（5） t(find(t==0))=eps（6）t=reshape(x,3,4)（7）abs('matlab')（8）char(93)5. A=[97,67,34,10;-78,75,65,5;32,5,-23,-59;0,-12,54,7](1) B=A(1:3,:)C=A(:,1:2)D=A(2:4,3:4)E=B*C(2)A(find(A>=50 & A<=100))二、实验题1.x=-74/180*pi;y=-27/180*pi;sin(x*x+y*y)/sqrt(tan(abs(x+y)))+pi2.a=-3.0:0.1:3.0;exp(-0.3*a).*sin(a+0.3)3.x=[2,4;-0.45,5];log(x+sqrt(1+x.*x))/24. A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0]; （1）A*Bans =129 432 41977 -407 -1052402 591 12489A.*Bans =3 -108 13468 -360 518783 270 0（2） A^3ans =-28917 240246 -4368137883 -259101 27669171333 252504 38673A.^3ans =27 157464 839304 -91125 343658503 729000 3375（3）A/Bans =-5.8845 5.3549 -0.20286.3554 -5.6596 4.3293-6.6325 6.2078 9.0241B/Aans =30.2855 19.2643 -8.561433.4394 21.1547 -9.3974-0.7443 -0.3938 0.2830（4）[A,B]ans =3 54 2 1 -2 6734 -45 7 2 8 7487 90 15 9 3 0[A([1,3],:);B^2]ans =3 54 287 90 15600 183 -81684 282 72615 6 8255.a=1+2i;b=3+4i;c=exp(pi*i/6)c =0.8660 + 0.5000ic+a*b/(a+b)ans =1.6353 + 1.8462i第2章一、思考题3.s=0;for n=0:63s=s+2^n;enddisp(s)n=0:63;s=sum(2.^n)二、实验题1.x=input('输入一个四位整数：');y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,10)] z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)2.gh=input('输入工号');h=input('输入工时');dj=84;if h>120gz=dj*120+1.15*dj*(h-120);elseif h<60gz=dj*h-700;elsegz=dj*h;endformat bank;display([gh,gz])3.循环结构n=input('input n:');s=0;for k=1:ns=s+1/k^2;enddisplay(sqrt(s*6))向量运算n=input('input n:');k=1:n;display(sqrt(sum(1./k.^2)*6))4.y=0;k=0;while y<3k=k+1;y=y+1/(2*k-1);enddisplay([k-1,y-1/(2*k-1)])5.x0=0;x=1;k=0;a=input('a=');b=input('b=');while abs(x-x0)>=1e-5 && k<500x0=x;x=a/(b+x0);k=k+1;enddisplay([k,x]);display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);6.y=fun(40)/(fun(30)+fun(20))（1）函数文件fun.mfunction f=fun(n)f=n+log(n^2+5);（2）函数文件fun.mfunction f=fun(n)a=1:n;f=sum(a.*(a+1));第3章一、思考题4.t=0:0.01:1.5;y=sqrt(3)/2*exp(-4*t).*sin(4*sqrt(3)*t+pi/3);5.x=-10:0.01:10;y=linspace(-6,6,size(x,2))z=x.^3+3*x.*y.^2;plot3(x,y,z)6.x=100:100:400;y=100:100:400;z=[636,697,624,478;698,712,630,478;680,674,598,412;662,626,552,334]; [X,Y]=meshgrid(x,y);mesh(X,Y,z)二、实验题1.（1）x=-10:0.01:10;plot(x,x-x.^3/3/2)（2）plot(x,exp(-x.*x/2)/2/pi)（3）x=-8:0.01:8;plot(x,sqrt((64-x.*x)/2))（4）t=0:pi/100:6*pi;plot(t.*sin(t),t.*cos(t))2. （1）x1=linspace(0,1,100);y1=2*x1-0.5;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);plot(x1,y1,'r-',x,y,'b:');text(0.4,1,'y=2x-0.5');text(-0.4,0.5,'x=sin(3t)cos(t)');text(-0.4,0.3,'y=sin(3t)sin(t)');（2）subplot(1,2,1);scatter(x1,y1,10)title('y=2x-0.5');subplot(1,2,2);scatter(x,y,10)3.subplot(1,21);x=1:1:100; y=sin(1./x);plot(x,y)subplot(1,2,2);fplot('sin(1/x)',[1,100])4.subplot(2,2,1);bar(t,y);subplot(2,2,2);stairs(t,y);subplot(2,2,3);stem(t,y)subplot(2,2,4);semilogy(t,y);5.theta=linspace(-pi,pi,100);ro=5.*cos(theta)+4;polar(theta,ro);fi=linspace(0,2*pi,100);a=1r=a.*(1+cos(fi));polar(fi,r);6.t=0:pi/20:2*pi;x=exp(-t./20).*cos(t);y=exp(-t./20).*sin(t);z=t; plot3(x,y,z);t=0:0.01:1;x=t;y=t.^2;z=t.^3;plot3(x,y,z);7.x=-30:0.1:0;y=0:0.1:30;[x,y]=meshgrid(x,y);z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2); meshc(x,y,z);8.x=linspace(-3,3,100);y=linspace(-3,3,100);[x y]=meshgrid(x,y);fxy=-5./(1+x.^2+y.^2);i=find(abs(x)<=0.8 & abs(y)<=0.5);fxy(i)=NaN;surf(x,y,fxy)9.u=linspace(1,10,100);v=linspace(-pi,pi,100);[u,v]=meshgrid(u,v);x=3.*u.*sin(v);y=2.*u.*cos(v);z=4*u.^2;x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.^2;surf(x,y,z);shading interp;light('position',[1,0,1]);10.t=0:pi/100:2*pi;y=sin(t);comet(t,y)第4章一、思考题5.（1）A=eye(3);（2）C=100+(200-100)*rand(5,6);（3）D=1+sqrt(0.2)*randn(1,500);（4）E=ones(size(A));（5）A=A+30*eye(size(A));（6）B=diag(diag(A))二、实验题1.P=pascal(5);H=hilb(5);Dp=det(P);Dh=det(H);Kp=cond(P);Kh=cond(H);P矩阵的性能更好，因为Kp较小2.A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3]B=[3,pi/2,45;32,-76,sqrt(37);5,72,4.5e-4;exp(2),0,97]A1=diag(A);B1=diag(B);A2=triu(A);B2=triu(B);A3=tril(A);B3=tril(B);rA=rank(A);rB=rank(B);nA=norm(A);nb=norm(B);cA=cond(A);cB=cond(B);3.A=[31,1,0;-4,-1,0;4,-8,-2]；[V,D]=eig(A);4.A=diag([-1,-1,-1,-1],-1)+diag([-1,-1,-1,-1],1)+diag([2,2,2,2,2]) b=[1,0,0,0,0]';x1=inv(A)*b;x2=A\b;[L,U]=lu(A);x3=U\(L\b);[Q,R]=qr(a);[Q,R]=qr(A);x4=R\(Q\b)R=chol(A);x5=R\(R'\b)5.B=sparse(A);x1=inv(B)*b;x2=B\b;[L,U]=lu(B);x3=U\(L\b);第5章一、思考题3.A=randn(10,5);mean(A)std(A)max(max(A))min(min(A))sum(A,2)sum(sum(A))sort(A,1)sort(A,2,'descend')二、实验题1.A=rand(1,30000);mean(A)std(A)max(A)min(A)size(find(A>0.5))/size(A)2.h=[466,715,950,1422,1635];w=[7.04,4.28,3.40,2.52,2.13];hh=[500,900,1500];ww=interp1(h,w,hh,'spline')3.x=linspace(1,10,50);y=log(x);f=polyfit(x,y,5);yy=polyval(f,x);plot(x,y,'r-',x,yy,'g.')4.N=64; % 采样点数T=5; % 采样时间终点t=linspace(0,T,N); % 给出N个采样时间ti(I=1:N) x=3*exp(-t); % 求各采样点样本值xdt=t(2)-t(1); % 采样周期f=1/dt; % 采样频率(Hz)X=fft(x); % 计算x的快速傅立叶变换XF=X(1:N/2+1); % F(k)=X(k)(k=1:N/2+1) f=f*(0:N/2)/N; % 使频率轴f从零开始plot(f,abs(F),'-*') % 绘制振幅-频率图xlabel('Frequency');ylabel('|F(k)|')5.（1）p1=[1 2 0 0 7];p2=[1 -2];p3=[1 0 0 5 1];p12=conv(p1,p2);p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3];roots(p)（2）A=[-1,4,3;2,1,5;0,5,6];Px=polyval(p,A)Pxm=polyvalm(p,A)6.（1）z=fzero('3*x-sin(x)+1',0)（2）建立函数文件myfun.mfunction F=myfun(X)x=X(1);y=X(2);F(1)=x*x+y*y-9;F(2)=x+y-1;在命令窗口中输入以下命令：x=fsolve(@myfun,[3,0]',optimset('Display','off')) 第6章一、思考题2.fx=inline('1./(1+x.^2)');[I,n]=quad(fx,-100000,100000,1e-3);[I,n]=quadl(fx,-100000,100000,1e-3);x=-100000:0.01:100000;y=1./(1+x.*x);trapz(x,y);3.(1)fx=inline('-2*y+2*x*x+2*x');[t,y]=ode23(fx,[0,0.5],1)(2)fx=inline('y-exp(x)*cos(x)');[t,y]=ode23(fx,[0,3],1)二、实验题1.for x=1:3fx=[x,x^2,x^3;1,2*x,3*x;0,2,6*x];diff(fx)end2.（1）x=0:0.01:1;y=x.^10+10.^x+1./log10(x);dy=diff(y)/0.01;（2）x=0:0.01:1;y=log(1+x);dy=diff(y,2)/0.01;plot(x(1:99),dy)3.（1）fx=inline('x.^2.*sqrt(2*x.*x+3)');quad(fx,1,5)（2）fx=inline('x./sin(x).^2');quad(fx,pi/4,pi/3)（3）fx=inline('abs(cos(x+y))');dblquad(fx,0,pi,0,pi)（4）syms x y ;fx=x*y;int(int(fx,y^2,y+2),-1,2)x 的积分区间为【0，2】时fx=inline('x.*y');dblquad(fx,0,2,-1,2)4.x=0.3:0.2:1.5;y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325]; trapz(x,y)5.（1）yp=inline('-(1.2+sin(10*x))*y');[t,y]=ode23(yp,[0,5],1);（2）令''3,,21y x y x y x ='==，则可写出原方程的状态方程形式：123233221sin 31)1(2cos 5cos x tx x t t t x x x x x +--++='='='⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'''t x x x t t t x x x cos 00)1(2cos 51sin 311000103212321 建立函数文件ztfun.mfunction y=ztfun(t,x)b=[0;0;cos(t)];y=[0,1,0;0,0,1;-1/(3+sin(t)),-1,5*cos(2*t)/(t+1)^2]*x+b; 解微分方程组[t,y]=ode23(@ztfun,[0,5],[1;0;2]);6.建立函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2)*y(3);-y(1)*y(3);-0.51*y(1)*y(2)];解微分方程组[t,y]=ode23(@ztfun,[0,5],[0;1;1])第7章一、思考题3.（1）数值积分fx=inline('exp(x).*(1+exp(x)).^2');quad(fx,0,log(2))符号积分f=sym('exp(x)*(1+exp(x))^2');v=int(f,0,log(2));eval(v)（2）略二、实验题1.A=sym('[1,2,3;x,y,z;3,2,1]')rank(A)inv(A)det(A)2.(1) y=sym('sqrt(x+sqrt(x+sqrt(x)))');y1=diff(y)y2=diff(y,'x',2)(2) syms x y;fxy=sin(x^2*y)*exp(-x^2-y);diff(diff(fxy,x),y)3.(1) syms xint(1/(1+x^4))(2) syms x tint((-2*x*x+1)/(2*x*x-3*x+1)^2,x,cos(t),exp(2*t)) 4.syms n xsymsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,inf)symsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,5)5.(1) syms xtaylor((exp(x)+exp(-x))/2,5,0)(2) syms a xtaylor(exp(-5*x)*sin(3*x+pi/3),5,a)6.(1)x=solve(sym('x^3+a*x+1=0'))(2) [x y]=solve(sym('sqrt(x^2+y^2)-100=0,3*x+5*y-8=0'))7. 方程转化为： π21'11't y y y y -=+=⎩⎨⎧符号解[y1,y11]=dsolve('Dy=y1,Dy1+y=1-t^2/pi','y(-2)=5,y1(-2)=5','t') 数值解编写函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2);1-t^2/pi-y(1)];在命令窗口输入以下命令[t,y]=ode45(@ztfun,[-2,7],[-5;5]);t=linspace(-2,7,49)y2=y8.[x,y]=dsolve('Dx=3*x+4*y,Dy=-4*x+3*y','x(0)=0,y(0)=1')。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第八章实验指导1、>> syms x y;>> A=x^4-y^4;>> factor(A)ans =(x - y)*(x + y)*(x^2 + y^2)>> a=5135;>> factor(a)ans =5 13 79 2、(1)>> syms x>> f=(x-2)/(x^2-4);>> limit(f,x,2)ans =1/4（2）>> syms xf=(sqrt(pi)-sqrt(acos(x)))/sqrt(x+1); limit(f,x,-1,'right')ans =-Inf3、（1）>> syms x y>> f=sin(1/x);>> diff(f)ans =-cos(1/x)/x^2>> diff(f,x,2)ans =(2*cos(1/x))/x^3 - sin(1/x)/x^4>> f=(1-cos(2x))/x;(2)>> f=(1-cos(2*x))/xf =-(cos(2*x) - 1)/x>> diff(f)ans =(2*sin(2*x))/x + (cos(2*x) - 1)/x^2 >> diff(f,x,2)ans =(4*cos(2*x))/x - (4*sin(2*x))/x^2 - (2*(cos(2*x) - 1))/x^3 4、(1)、>> x=sym('x');>> f=sqrt(exp(x)+1);>> int(f)ans =atan((exp(x) + 1)^(1/2)*i)*2*i + 2*(exp(x) + 1)^(1/2) (2)>> x=sym('x');y=sym('y');f=x/(x+y);>> int(f,y)ans =x*log(x + y)(3)>> syms x;>> f=exp(x)*(exp(x)+1)^2;>> int(f,0,log10(2))ans =(exp(5422874305198591/18014398509481984)*(3*exp(5422874305198 591/18014398509481984) + exp(5422874305198591/9007199254740992) + 3))/3 - 7/3(4)>> sym('x');f=x*log10(x);int(f,1,exp(1))ans =(18733482797859000068490812234738*log(3060513257434037/112589 9906842624) -8099090798701270632748702911993)/(50706024009129176059868128 21504*log(10))5、(1)>> s=symsum((-1)^(n+1)*1/n,1,inf)s =log(2)(2)>> syms n>> s=symsum(x^(2*n-1)/(2*n-1),1,inf)s =piecewise([real(n) < 0, zeta(1 - 2*n)/(2*n - 1)]) 6、(1)>> syms x;>> f=(exp(x)+exp(-1*x))/2;>> taylor(f,x,5,0)ans =x^4/24 + x^2/2 + 1(2)>> syms x;>> f=sqrt(x^3-2*x+1);>> taylor(f,x,6,0)ans =- x^5/8 - x^4/8 - x^2/2 - x + 17、(1)>> syms x a;x=solve('x^3+a*x+1','x')x =((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3) - a/(3*((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3))(3^(1/2)*(a/(3*((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3)) + ((a^3/27 + 1/4)^(1/2) -1/2)^(1/3))*i)/2 + a/(6*((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3)) - ((a^3/27 +1/4)^(1/2) - 1/2)^(1/3)/2a/(6*((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3)) - (3^(1/2)*(a/(3*((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3)) + ((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3))*i)/2 - ((a^3/27 + 1/4)^(1/2) - 1/2)^(1/3)/2(2)>> syms x>> x=solve('sin(x)+2*cos(x)-sqrt(x)=0','x')x =- 227.29614717392215108027554049443 + 2.607041909691930054078218073756*i （3）>> syms x y;>> [x y]=solve('log10(x/y)=9','exp(x+y)=3','x','y') x =(1000000000*log(3))/1000000001y =log(3)/10000000018、思考练习1、(1)数值计算>> 1/2+2/3ans =1.1667符号运算>> p1=sym('1/2'); >> a=sym('2/3'); >> p1+aans =7/6(2)数值计算>> pi+sqrt(5)ans =5.3777 >> a=sym('36'); >> y=36;>> (1+sqrt(a))/2ans =7/2>> c=sym('pi'); >> d=sym('sqrt(5)'); >> c+dans =pi + 5^(1/2)(3)数值计算>> (1+sqrt(36))/2ans =3.5000符号计算>> a=sym('36'); >> y=36;>> (1+sqrt(a))/2ans =2、>> syms x B1 B2 a bs1=2*((cos(x))^2)-(sin(x))^2;s2=sin(B1)*cos(B2)-cos(B1)*sin(B2);s3=sqrt((a+sqrt(a^2-b))/2)+sqrt((a-sqrt(a^2-b))/2); s4=(4*x^2+8*x+3)/(2*x+1);h1=simplify(s1)h2=simplify(s2)h3=simplify(s3)h4=simplify(s4)h1 =3*cos(x)^2 - 1h2 =sin(B1 - B2)(2^(1/2)*((a + (a^2 - b)^(1/2))^(1/2) + (a - (a^2 - b)^(1/2))^(1/2)))/2 h4 =2*x + 33、>> syms x a;f=abs(x)/x;limit(f,x,0,'left')ans =-1(2)>> f=(x+a/x)^x;limit(f,x,inf)ans =4、(1)>> syms x y mf=sqrt(x+sqrt(x+sqrt(x)));m=diff(f,'x')diff(m,'x')m =((1/(2*x^(1/2)) + 1)/(2*(x + x^(1/2))^(1/2)) + 1)/(2*(x + (x +x^(1/2))^(1/2))^(1/2))ans =- ((1/(2*x^(1/2)) + 1)/(2*(x + x^(1/2))^(1/2)) + 1)^2/(4*(x + (x +x^(1/2))^(1/2))^(3/2)) - (1/(8*x^(3/2)*(x + x^(1/2))^(1/2)) + (1/(2*x^(1/2)) +1)^2/(4*(x + x^(1/2))^(3/2)))/(2*(x + (x + x^(1/2))^(1/2))^(1/2))(2)>> syms x y;f=x+y-sqrt(x^2+y^2);z1=diff(f,x)z2=diff(f,y)z1 =1 - x/(x^2 + y^2)^(1/2)z2 =1 - y/(x^2 + y^2)^(1/2)5、>> syms x;>> f=1/sin(x);>> int(f)ans =log(tan(x/2))(2)>> sym x;f=1/(asin(x)^2*(1-x^2)^(1/2)); int(f)ans =-1/asin(x)5、(1)>> syms x>> f=1/(1+sqrt(x));>> int(f,0,4)ans =4 - log(9)(2) sym x;f=x^3*sin(x)^2/(x^6+2*x^4+1);int(f,-1,1)Warning: Explicit integral could not be found. ans =int((x^3*sin(x)^2)/(x^6 + 2*x^4 + 1), x == -1..1) 7、(1)>> syms ns=symsum(1/4^n,1,inf)s =1/3(2)、>> sym n;s=symsum(((n+1)/n)^(1/2),1,inf) eval(y)s =sum(((n + 1)/n)^(1/2), n == 1..Inf) ans =y8、（1）>> syms xf=tan(x);taylor(f,x,3,0)x(2)、>> syms xf=sin(x)^2;taylor(f,x,5,0)ans =- x^4/3 + x^29、(1)>> syms xx=solve('log(1+x)-5/(1+sin(x))=2','x')x =521.67926389905839979437366649258(2)syms x y z>> [x yz]=solve('4*x^2/(4*x^2+1)=y','4*y^2/(4*y^2+1)=z','4*z^2/(4*z^2+1)=x','x' ,'y','z')1/2- 20.0*z^5 - 21.617977528089887640449438202247*z^4 - 1.2359550561797752808988764044944*z^3 +3.6741573033707865168539325842697*z^2 -0.058988764044943820224719101123596*z -0.011235955056179775280898876404494y =1/2156.0*z^5 + 110.82022471910112359550561797753*z^4 + 10.404494382022471910112359550562*z^3 +2.5337078651685393258426966292135*z^2 +0.30056179775280898876404494382022*z +0.097612359550561797752808988764045z =1/2Z10、>> [x ,y]=dsolve('Dx=3*x+4*y','Dy=5*x-7*y','x(0)=0','y(0)=1','t')x =-(exp(-t*(3*5^(1/2) + 2))*((3*5^(1/2))/2 - (5^(1/2)*(3*5^(1/2) + 5))/6 +5*exp(t*(3*5^(1/2) - 2))*exp(t*(3*5^(1/2) + 2))*(5^(1/2)/6 - 1/2) +3*5^(1/2)*exp(t*(3*5^(1/2) - 2))*exp(t*(3*5^(1/2) + 2))*(5^(1/2)/6 - 1/2) + 5/2))/5y =exp(-t*(3*5^(1/2) + 2))*((5^(1/2)*(3*5^(1/2) + 5))/30 - exp(t*(3*5^(1/2) - 2))*exp(t*(3*5^(1/2) + 2))*(5^(1/2)/6 - 1/2))。