matlab课后答案完整版

MATLAB）课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值，然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。

(1) 0122sin851z e =+(2) 221ln(1)2z x x =++，其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ?≤=-≤，其中t =0:0.5:2.5 解： M ⽂件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5]; z2=1/2*log(x+sqrt(1+x^2)) a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建⽴⼀个字符串向量，删除其中的⼤写字母。

解：(1) 结果：m=100:999;n=find(mod(m,21)==0);length(n)ans =43(2). 建⽴⼀个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch =实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵，试通过数值计算验证22E R RS A O S +??=。

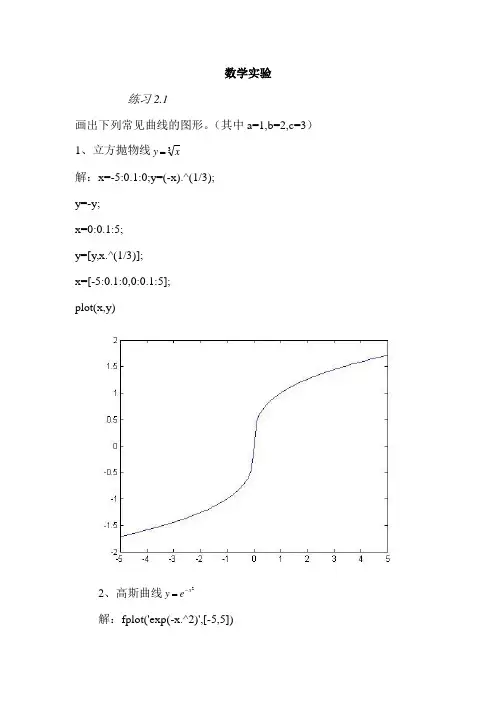
数学实验练习2.1画出下列常见曲线的图形。

（其中a=1,b=2,c=3）1、立方抛物线3xy=解：x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解：fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解：ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解：ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解：t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解：t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解：t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解：x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解：x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解：x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解：x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解：x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。

matlab习题及答案Matlab习题及答案Matlab是一种强大的数学计算软件，被广泛应用于科学计算、数据分析和工程设计等领域。

在学习和使用Matlab的过程中，习题是一种非常有效的学习方式。

本文将给出一些常见的Matlab习题及其答案，帮助读者更好地掌握Matlab的使用技巧。

一、基础习题1. 计算1到100之间所有奇数的和。

解答：```matlabsum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```2. 编写一个函数，计算任意两个数的最大公约数。

解答：```matlabfunction gcd = computeGCD(a, b)while b ~= 0temp = b;a = temp;endgcd = a;end```3. 编写一个程序，生成一个5×5的随机矩阵，并计算矩阵的行和列的平均值。

解答：```matlabmatrix = rand(5);row_average = mean(matrix, 2);col_average = mean(matrix);disp(row_average);disp(col_average);```二、进阶习题1. 编写一个程序，实现插入排序算法。

解答：```matlabfunction sorted_array = insertionSort(array)n = length(array);for i = 2:nj = i - 1;while j > 0 && array(j) > keyarray(j+1) = array(j);j = j - 1;endarray(j+1) = key;endsorted_array = array;end```2. 编写一个程序，实现矩阵的转置。

解答：```matlabfunction transposed_matrix = transposeMatrix(matrix) [m, n] = size(matrix);transposed_matrix = zeros(n, m);for i = 1:mfor j = 1:ntransposed_matrix(j, i) = matrix(i, j);endendend```3. 编写一个程序，实现二分查找算法。

习题二之阳早格格创做1.怎么样明白“矩阵是MATLAB最基础的数据对于象”？问：果为背量不妨瞅成是仅有一止或者一列的矩阵，单个数据（标量）不妨瞅成是仅含一个元素的矩阵，故背量战单个数据皆不妨动做矩阵的惯例去处理.果此，矩阵是MATLAB最基础、最要害的数据对于象.2.设A战B是二个共维共大小的矩阵，问：(1)A*B战A.*B的值是可相等？问：没有相等.(2)A./B战B.\A的值是可相等？问：相等.(3)A/B战B\A的值是可相等？问：没有相等.(4)A/B战B\A所代表的数教含意是什么？问：A/B等效于B的顺左乘A矩阵，即A*inv(B)，而B\A等效于B矩阵的顺左乘A矩阵，即inv(B)*A.3.写出完毕下列支配的下令.(1)将矩阵A第2~5止中第1, 3, 5列元素赋给矩阵B.问：B=A(2:5,1:2:5); 或者B=A(2:5,[1 3 5])(2)简略矩阵A的第7号元素.问：A(7)=[](3)将矩阵A的每个元素值加30.问：A=A+30;(4)供矩阵A的大小战维数.问：size(A);ndims(A);(5)将背量t的0元素用呆板整去代替.问：t(find(t==0))=eps;(6)将含有12个元素的背量x变换成34 矩阵.问：reshape(x,3,4);(7)供一个字符串的ASCII码.问：abs(‘123’); 或者double(‘123’);(8)供一个ASCII码所对于应的字符.问：char(49);4.下列下令真止后，L1、L2、L3、L4的值分别是几？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);问：L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知完毕下列支配：(1)与出A的前3止形成矩阵B，前二列形成矩阵C，左下角32⨯子矩阵形成矩阵D，B与C的乘积形成矩阵E.问：B=A(1:3,:);C=A(:,1:2);D=A(2:4,3:4);E=B*C;(2)分别供E<D、E&D、E|D、~E|~D战find(A>=10&A<25).问：E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E|D=111111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，~E|~D=001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦find(A>=10&A<25)=[1; 5].6.当A=[34, NaN, Inf, -Inf, -pi, eps, 0]时，分解下列函数的真止截止：all(A)，any(A)，isnan(A)，isinf(A)，isfinite(A).问：all(A)的值为0any(A)的值为1isnan(A)的值为[0, 1, 0, 0, 0, 0, 0]isinf(A)的值为[0, 0, 1, 1, 0, 0, 0]isfinite(A)的值为[1, 0, 0,0, 1, 1, 1]7.用结构体矩阵去保存5名教死的基础情况数据，每名教死的数据包罗教号、姓名、博业战6门课程的结果.问：student(1).id='0001';student(1).name='Tom';student(1).major='computer';student(1).grade=[89,78,67,90,86,85];8.修坐单元矩阵B并回问有闭问题.B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)战ndims(B)的值分别是几？问：size(B)的值为2,2.ndims(B)的值为2.(2)B(2)战B(4)的值分别是几？问：B(2)=147258369⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，B(4)=[12][34][2][54][21][3][4][23][67]⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(3)B(3)=[]战B{3}=[]真止后，B的值分别是几？问：当真止B(3)=[]后，B={1, [1, 4, 7; 2, 5, 8; 3, 6, 9], {12, 34, 2; 54, 21, 3; 4, 23, 67}}当真止B{3}=[]后，B={1,[]; [1, 4, 7; 2, 5, 8; 3, 6, 9],{12, 34, 2; 54, 21, 3; 4, 23, 67}}习题三1.写出完毕下列支配的下令.(1)修坐3阶单位矩阵A.问：A=eye(3);(2)修坐5×6随机矩阵A，其元素为[100,200]范畴内的随机整数.问：round(100+(200-100)*rand(5,6));(3)爆收均值为1，圆好为0.2的500个正态分散的随机数.问：1+sqrt(0.2)*randn(5,100);(4)爆收战A共样大小的幺矩阵.问：ones(size(A));(5)将矩阵A对于角线的元素加30.问：A+eye(size(A))*30;(6)从矩阵A提与主对于角线元素，并以那些元素形成对于角阵B.问：B=diag(diag(A));2.使用函数，真止圆阵左旋90o或者左旋90o的功能.比圆，本矩阵为A，A左旋后得到B，左旋后得到C.问：B=rot90(A);C=rot90(A,-1);3.修坐一个圆阵A，供A的顺矩阵战A的止列式的值，并考证A与A-1是互顺的.问：A=rand(3)*10;B=inv(A);C=det(A);先估计B*A，再估计A*B，由估计可知B*A=A*B，即A·A-1=A-1·A是互顺.4.供底下线性圆程组的解.问：A=[4,2,-1;3,-1,2;12,3,0];b=[2;10;8];x=inv(A)*b圆程组的解为x=6.000026.666727.3333 -⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦5.供下列矩阵的主对于角线元素、上三角阵、下三角阵、秩、范数、条件数战迹.(1)112351423052111509A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦(2)0.434328.9421B⎡⎤=⎢⎥-⎣⎦问：(1)与主对于角线元素：diag(A);上三角阵：triu(A)；下三角阵：tril(A);秩：rank(A);范数：norm(A,1); 或者 norm(A);或者 norm(A,inf);条件数：cond(A,1); 或者 cond(A,2); 或者 cond(A,inf)迹：trace(A);(2)【请参照(1)】.6.供矩阵A的特性值战相映的特性背量.问：[V,D]=eig(A);习题四1.从键盘输进一个4位整数，按如下准则加稀后输出.加稀准则：每位数字皆加上7，而后用战除以10的余数与代该数字；再把第一位与第三位接换，第二位与第四位接换.问：a=input('请输进4位整数：');A=[a/1000,a/100,a/10,a];A=fix(rem(A,10));A=rem(A+7,10);b=A(3)*1000+A(4)*100+A(1)*10+A(2);disp(['加稀后的值为：',num2str(b)]);2.分别用if语句战switch语句真止以下估计，其中a、b、c 的值从键盘输进.问：(1) 用if语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');y=a*x^2+b*x+c;endy=a*((sin(b))^c)+x;endy=log(abs(b+c/x));enddisp(['y=',num2str(y)]);(2) 用switch语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');switch fix(x/0.5)case {1,2}y=a*x^2+b*x+c;case num2cell(3:6)y=a*((sin(b))^c)+x;case num2cell(7:10)y=log(abs(b+c/x));enddisp(['y=',num2str(y)]);3.爆收20个二位随机整数，输出其中小于仄衡值的奇数.问：A=fix(10+89*rand(1,20));sum=0;for i=1:20sum=sum+A(i);endB=A(find(A<(sum/20)));C=B(find(rem(B,2)==0));disp(C);4. 输进20个数，供其中最大数战最小数.央供分别用循环结媾战调用MATLAB 的max 函数、min 函数去真止. 问：(1) 用循环结构真止：v_max=0;v_min=0;for i=1:20x=input(['请输进第', num2str(i), '数：']);if x>v_maxv_max=x;end;if x<v_minv_min=x;end;enddisp(['最大数为：', num2str(v_max)]);disp(['最小数为：', num2str(v_min)]);(2) 用max 函数、min 函数真止：for i=1:5A(i)=input(['请输进第', num2str(i), '数：']);enddisp(['最大数为：', num2str(max(A))]);disp(['最小数为：', num2str(min(A))]);5. 已知：236312222s =+++++，分别用循环结媾战调用MATLAB 的sum 函数供s 的值.问：(1) 用循环结构真止：s=0;for i=0:63s=s+2^i;ends(2) 调用sum函数真止：s=0:63;s=2.^s;sum(s)6.当n分别与100、1000、10000时，供下列各式的值.(1)111111(1)(ln2) 234nn+-+-++-+=(2)1111() 3574π-+-+=(3) 11111() 4166443n+++++=(4)224466(2)(2)133557(21)(21)2n nn nπ⎛⎫⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎛⎫=⎪⎪⎪⎪ ⎪⨯⨯⨯-⨯+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭央供分别用循环结媾战背量运算（使用sum或者prod函数）去真止.问：(1) 用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/k;endsum使用sum函数：x=[];for k=1:10000x=[x, (-1)^(k+1)/k];endsum(x)(2)用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/(2*k-1);endsum使用sum函数：x=[];for k=1:100x=[x, (-1)^(k+1)/(2*k-1)];endsum(x)(3)用循环结构真止：sum=0;for k=1:100sum=sum+1/(4^k);endsum使用sum函数真止：x=[];for k=1:100x=[x, 1/(4^k)];endsum(x)(4)用循环结构真止：t=1;for k=1:100t=t*(((2*k)*(2*k))/((2*k-1)*(2*k+1)));endt使用prod函数真止：x=[];for k=1:100x=[x, ((2*k)*(2*k))/((2*k-1)*(2*k+1))];endprod(x)7. 编写一个函数文献，供小于任性自然数n的斐波那契（Fibnacci）数列各项.斐波那契数列定义如下：问：function x=fibnacci(n)for i=1:nif i<=2x(i)=1;elsex(i)=x(i-1)+x(i-2);endend8.编写一个函数文献，用于供二个矩阵的乘积战面乘，而后正在下令文献中调用该函数.问：函数文献myfnc.m：function [x, y]=myfnc(A, B)tryx=A*B;catchx=[];endy=A.*B;下令文献myexe.m：A=input('请输进矩阵A：');B=input('请输进矩阵B：');[x, y]=myfnc(A, B);if length(x)==0display('二矩阵的维数没有匹配，无法举止乘积运算！');disp('矩阵A 战矩阵B 的乘积为：'); xenddisp('矩阵A 战矩阵B 的面乘为：'); y9. 先用函数的递归调用定义一个函数文献供1n m i i =∑，而后调用该函数文献供100501021111k k k k k k ===++∑∑∑. 问：函数文献myfnc.m ：function sum=myfnc(n, m)if n<=1sum=1;elsesum= myfnc (n-1, m)+n^m;end正在下令窗心中调用myfnc.m 文献，估计100501021111k k k k k k ===++∑∑∑： sum=myfnc(100, 1)+myfnc(50, 2)+myfnc(10,-1) 10.写出下列步调的输出截止.① s=0;a=[12,13,14;15,16,17;18,19,20;21,22,23]; for k=afor j=1:4if rem(k(j),2)~=0s=s+k(j);endendends问：真止截止为②下令文献exe.m真止后的截止为：x =41220y=2 4 6。

实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MA TLAB 工作空间的使用情况并保存全部变量。

(1) 0122sin 851z e=+(2) 21ln(2z x =+，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦(3) 0.30.330.3sin(0.3)ln,3.0, 2.9,,2.9,3.022aaee a z a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.52. 已知：1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：(1) A+6*B 和A-B+I （其中I 为单位矩阵） (2) A*B 和A.*B(3) A^3和A.^3(4) A/B及B\A(5) [A,B]和[A([1,3],:);B^2]3. 设有矩阵A 和B1234530166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。

(2) 将矩阵C 的右下角3×2子矩阵赋给D 。

(3) 查看MA TLAB 工作空间的使用情况。

4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

(2). 建立一个字符串向量 例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R R S A OS +⎡⎤=⎢⎥⎣⎦。

Matlab课后实验题答案实验一 MATLAB运算基础1. 先求下列表达式的值，然后显示MATLAB工作空间的使用情况并保存全部变量。

(1)0 122sin851ze =+(2)21ln( 2z x=+，其中2120.455i x+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--L(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t=0:0.5:2.52. 已知：1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：(1) A+6*B 和A-B+I （其中I 为单位矩阵） (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2] 解：3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。

(2) 将矩阵C 的右下角3×2子矩阵赋给D 。

(3) 查看MATLAB 工作空间的使用情况。

4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：(2). 建立一个字符串向量 例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。

matlab习题及答案《Matlab习题及答案：提升编程技能，解决实际问题》Matlab是一种强大的数值计算和数据分析工具，它被广泛应用于工程、科学和其他领域的计算和模拟。

为了帮助大家提升编程技能，解决实际问题，我们为大家准备了一些Matlab习题及答案，希望能够帮助大家更好地掌握Matlab的使用。

1. 习题一：编写一个Matlab程序，计算斐波那契数列的前20个数字，并将结果打印出来。

答案：下面是一个简单的Matlab程序，用于计算斐波那契数列的前20个数字。

```matlaba = 0;b = 1;fib = zeros(1, 20);fib(1) = a;fib(2) = b;for i = 3:20fib(i) = fib(i-1) + fib(i-2);enddisp(fib);```2. 习题二：编写一个Matlab程序，求解一个二次方程ax^2 + bx + c = 0的根。

答案：下面是一个简单的Matlab程序，用于求解二次方程的根。

```matlaba = 1;b = -3;c = 2;delta = b^2 - 4*a*c;if delta > 0x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);disp(['The roots are ', num2str(x1), ' and ', num2str(x2)]);elseif delta == 0x = -b/(2*a);disp(['The root is ', num2str(x)]);elsedisp('The equation has no real roots');end```通过以上两个习题及答案的示例，我们可以看到Matlab的强大功能和灵活性。

通过练习这些习题，我们可以更好地掌握Matlab的基本语法和常用函数，从而在实际问题中更快更准确地解决数值计算和数据分析的挑战。

第2章符号运算习题2及解答1 说出以下四条指令产生的结果各属于哪种数据类型，是“双精度”对象，还是“符号”符号对象？3/7+0.1; sym(3/7+0.1); sym('3/7+0.1'); vpa(sym(3/7+0.1))〖目的〗●不能从显示形式判断数据类型，而必须依靠class指令。

〖解答〗c1=3/7+0.1c2=sym(3/7+0.1)c3=sym('3/7+0.1')c4=vpa(sym(3/7+0.1))Cs1=class(c1)Cs2=class(c2)Cs3=class(c3)Cs4=class(c4)c1 =0.5286c2 =37/70c3 =c4 =Cs1 =doubleCs2 =symCs3 =symCs4 =sym2 在不加专门指定的情况下，以下符号表达式中的哪一个变量被认为是自由符号变量.sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)')〖目的〗●理解自由符号变量的确认规则。

〖解答〗symvar(sym('sin(w*t)'),1)ans =wsymvar(sym('a*exp(-X)'),1)ans =asymvar(sym('z*exp(j*th)'),1) ans = z5求符号矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A 的行列式值和逆，所得结果应采用“子表达式置换”简洁化。

〖目的〗● 理解subexpr 指令。

〖解答〗A=sym('[a11 a12 a13;a21 a22 a23;a31 a32 a33]')DA=det(A) IA=inv(A);[IAs,d]=subexpr(IA,d) A =[ a11, a12, a13] [ a21, a22, a23] [ a31, a32, a33] DA =a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31 IAs = [ d*(a22*a33 - a23*a32), -d*(a12*a33 - a13*a32), d*(a12*a23 - a13*a22)] [ -d*(a21*a33 - a23*a31), d*(a11*a33 - a13*a31), -d*(a11*a23 - a13*a21)] [ d*(a21*a32 - a22*a31), -d*(a11*a32 - a12*a31), d*(a11*a22 - a12*a21)] d =1/(a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31)8（1）通过符号计算求t t y sin )(=的导数dtdy。

第二章%分段函数的写法syms y xz=int(x*y,x,0,1);g = evalin(symengine,[' piecewise([y > 1/2,' char(z) '], [y <= 1/2, 1])']) G=int(g,y)g =piecewise([1/2 < y, y/2], [y <= 1/2, 1])G =piecewise([1/2 < y, y^2/4], [y <= 1/2, y])%习题2-1class(vpa(sym(3/7+0.1),4))%习题2-2findsym(sym('sin(w*t)'),1)findsym(sym('a*exp(-X)'),1)findsym(sym('z*exp(j*th)'),1)%习题2-3syms x a positivex_1=solve('x^3-44.5')syms x unrealx_2=solve('x^2-a*x+a^2')syms a unrealx_2=solve('x^2-a*x+a^2')x_3=solve('x^2-a*x-a^2')syms x realevalin(symengine,'anames(Properties)')evalin(symengine,'getprop(x)')%习题2-47/3, pi/3 , pi*3^(1/3)a = pi*3^(1/3) ,b = sym( pi*3^(1/3) ),c = sym( pi*3^(1/3),'d'),d = sym( 'pi*3^(1/3) ' )vpa(abs(a-d)) , vpa(abs(b-d)) , vpa(abs(c-d))%习题2-5syms a11 a12 a13 a21 a22 a23 a31 a32 a33A = [a11 a12 a13;a21 a22 a23;a31 a32 a33]a=det(A)B=inv(A)C=subexpr(B)[RS,w]=subexpr(B,'w')%习题2-6syms ksyms a positive% fk =a^k * heaviside(k)fk =a^ks=symsum(fk,k,0,inf)%习题2-7clear allsyms ksyms x positivefk =2/(2*k+1)*(((x-1)/(x+1))^(2*k+1))s=symsum(fk,k,0,inf)s1=simple(s)%习题2-8clear all, syms ty=abs(sin(t))df=diff(y),class(df)df1=limit(df,t,0,'left')df2=subs(df,'t',sym(pi/2))%习题2-9clear all, syms x;f=exp(-abs(x)).*abs(sin(x));fint=int(f,x,-5*pi,1.7*pi), digits(64), vpa(fint)class(fint)%习题2-10clear all,syms x y,f=x.^2+y.^2,fint=(int(int(f,y,1,x.^2),x,1,2)), double(fint)%习题2-11clear all, syms t x; f=sin(t)/t, yx=int(f,t,0,x), ezplot(yx,[0 2*pi])fint=subs(yx,x,4.5),%或yxd=int(f,t,0,4.5),fint=double(yxd)hold on, plot(4.5,fint,'*r')%习题2-12% clear all, syms x n; f=(sin(x))^n; yn=int(f,'x',0,pi/2), class(yn)clear all, syms x n; syms n positive ; f=(sin(x))^n; yn=int(f,'x',0,pi/2), class(yn) % y(1/3)=?yn1=subs(yn,'n',sym(1/3)),vpa(yn1)%或yn=limit(yn,n,1/3),vpa(yn)%或yy=int(sin(x).^(1/3),x,0,pi/2) ,vpa(yy)%习题2-23clear, syms x y SS = dsolve('Dy*y/5+x/4=0','x')ezplot(subs(S(1),'C3',1),[-2,2 -2,2],1), hold onezplot(subs(S(2),'C3',1),[-2,2 -2,2],1)%解为S =% 2^(1/2)*(C3 - (5*x^2)/8)^(1/2)% -2^(1/2)*(C3 - (5*x^2)/8)^(1/2)ezplot(subs(S(1),'C3',1),[-2,2 -2,2],1), hold onezplot(subs(S(2),'C3',1),[-2,2 -2,2],1) % 用此两条指令绘圆，在y=0处有间隙ezplot(subs(y^2-(S(1))^2, 'C3', 1),[-2,2 -2,2],2) %用椭圆方程绘图不产生间隙colormap([0 0 1]) %用ezplot(fun)绘图时，如果fun中只有一个参数，绘图的颜色是蓝色；如果fun中有两个参数，绘图的颜色是绿色，此指令设置图形颜色为蓝。

1、利用基本矩阵产生3*3和15*8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机阵（[-1,1]之间）、正态分布随机阵（均值为1，方差为4）。

解：A1=eye(3); A2=ones(3); A3=zeros(3); A4=2*rand(3)-1; A5=2*randn(3)+1;B1=eye(15,8); B2=ones(15,8); B3=zeros(15,8); B4=2*rand(15,8)-1; B5=2*randn(15,8)+1; 结果：由于数据是随机产生的，所以在没有给出运行结果。

2、利用diag等函数产生下列矩阵：a=[0 0 8;0 -7 5;2 3 0] b=[2 0 4;0 5 0;7 0 8]然后利用reshape函数将它们变换成行向量。

解：产生a的程序：b=diag([8 -7 2]);c=b+diag([5 3],-1);a=fliplr(c)产生b的程序：s=[2 2 8];t=[4 3 7];v=diag(s);p=diag(t)+fliplr(v);b=fliplr(p)运行结果：a =0 0 80 -7 52 3 0b =2 0 40 5 07 0 8利用reshape函数将它们变换成行向量：reshape(a,1,9)ans =0 0 2 0 -7 3 8 5 03、产生一均匀分布在（-5,5）之间的随机阵（50*2），要求精确到小数点后一位。

解：A=5-round(100*rand(50,2))/10部分数据结果：A =2.4000 4.2000-0.1000 2.7000-4.6000 -3.3000-0.5000 -0.40003.50004.20004、编程实现当t∈[-π,π],间隔为1°时求解正弦和余弦值。

解：t=(-1*pi:1/180:pi);y1=sin(t)y2=cos(t)部分数据结果：Columns 10 through 18（y1）-0.0500 -0.0555 -0.0611 -0.0666 -0.0722 -0.0777 -0.0832 -0.0888 -0.09435、利用rand函数产生（0,1）间的均匀分布的10*10随机矩阵A，然后统计A中大于等于0.6的元素的个数。

数学实验MATLAB参考答案（重要部分）P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值，b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明：编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明：编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1，但数据类型分别为数值，字符，逻辑，注意a 与c相等，但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6579 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3423 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数，保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2])(2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20);[theta,fai]=meshgrid(theta,fai); x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\ page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000 -1.00002.0000 1.0000 -0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b]) ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0 Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例，说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]'; >> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.0100 0.1200 0.0400 0.0900 >> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500 -0.0900 0.8000 -0.0100 -0.1200 -0.0400 0.9100 >> D=[17 17 17]';x=A\D x =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一（三个for）n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二（一个for）n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三（不用for）n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关，可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关，不可对角化>> [v,d]=jordan(a)v =1 0 11 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的，所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组3>> b=a([1 2 4],:)';c=a([3 5],:)'; >> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467%Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3))fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013%Exercise 1(1)roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi; x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置，然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小，x(2)(4)(6)是局部极大，从最后一句知道x(1)全局最小， x(2)最大。

matlab课后习题答案刘
《MATLAB课后习题答案刘》
MATLAB是一种强大的数学软件，广泛应用于工程、科学和数学领域。

在学习MATLAB的过程中，课后习题是巩固知识、提高能力的重要途径。

为了帮助学生更好地掌握MATLAB知识，我们特为大家整理了一份MATLAB课后习题答案刘，希望对大家有所帮助。

1. 问题一：编写一个MATLAB程序，计算1到100之间所有偶数的和。

解答：可以使用for循环结合if语句来实现这个问题。

具体代码如下：
```matlab
sum = 0;
for i = 1:100
if mod(i, 2) == 0
sum = sum + i;
end
end
disp(sum);
```
2. 问题二：编写一个MATLAB程序，计算给定数组的平均值。

解答：可以使用mean函数来计算数组的平均值。

具体代码如下：
```matlab
A = [1, 2, 3, 4, 5];
avg = mean(A);
disp(avg);
```
3. 问题三：编写一个MATLAB程序，绘制正弦函数的图像。

解答：可以使用plot函数来绘制正弦函数的图像。

具体代码如下：
```matlab
x = 0:0.01:2*pi;
y = sin(x);
plot(x, y);
```
通过以上几个例子，我们可以看到MATLAB的强大之处。

希望大家在学习MATLAB的过程中能够多加练习，不断提高自己的编程能力。

如果还有其他问题，欢迎随时向我们咨询。

祝大家学习进步！。

5. 下面是一个线性方程组：
1112340.95x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥
实验三 选择结构程序设计
1. 求分段函数的值。

222603560523
1x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩
且且及其他用if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

解：M 文件如下：
2. 输入一个百分制成绩，要求输出成绩等级A、B、C、D、E。

其中90分~100分为A，80分~89分为B，79分~79分为C，60分~69分为D，60分以下为E。

要求：
(1) 分别用if语句和switch语句实现。

(2) 输入百分制成绩后要判断该成绩的合理性，对不合理的成绩应输出出错信息。

解：M文件如下
3. 硅谷公司员工的工资计算方法如下：
(1) 工作时数超过120小时者，超过部分加发15%。

(2) 工作时数低于60小时者，扣发700元。

(3) 其余按每小时84元计发。

试编程按输入的工号和该号员工的工时数，计算应发工资。

解：M文件下
运算结果如下；
5. 若两个连续自然数的乘积减1是素数，则称这两个边疆自然数是亲密数对，该素数是亲密素数。

例如，2×3-1=5，由于5是素数，所以2和3是亲密数，5是亲密素数。

求[2,50]区间内：
(1) 亲密数对的对数。

(2) 与上述亲密数对对应的所有亲密素数之和。

解：
M文件：。

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”？答：因为向量可以看成是仅有一行或一列的矩阵，单个数据（标量）可以看成是仅含一个元素的矩阵，故向量和单个数据都可以作为矩阵的特例来处理。

因此，矩阵是MATLAB最基本、最重要的数据对象。

2.设A和B是两个同维同大小的矩阵，问：(1)A*B和A.*B的值是否相等？答：不相等。

(2)A./B和B.\A的值是否相等？答：相等。

(3)A/B和B\A的值是否相等？答：不相等。

(4)A/B和B\A所代表的数学含义是什么？答：A/B等效于B的逆右乘A矩阵，即A*inv(B)，而B\A等效于B矩阵的逆左乘A矩阵，即inv(B)*A。

3.写出完成下列操作的命令。

(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。

答：B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。

答：A(7)=[](3)将矩阵A的每个元素值加30。

答：A=A+30;(4)求矩阵A的大小和维数。

答：size(A);ndims(A);(5)将向量t的0元素用机器零来代替。

答：t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34矩阵。

答：reshape(x,3,4);(7)求一个字符串的ASCII码。

答：abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符。

答：char(49);4.下列命令执行后，L1、L2、L3、L4的值分别是多少？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答：L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知完成下列操作：(1)取出A的前3行构成矩阵B，前两列构成矩阵C，右下角32⨯子矩阵构成矩阵D，B 与C的乘积构成矩阵E。

MATLAB仿真课后习题答案第一章1.要求在闭区间[0，2Π]上产生具有10个等间距采样点的一维数组。

试用两种不同的指令实现。

解答：方法1：a=0:2*pi/9:2*pi方法2：a1=linspace(0,2*pi,10)4.任意建立矩阵A，然后找出在[10,20]区间的元素的位置。

解答：A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式：命令文件和函数文件。

命令文件没有输入输出参数，执行时只需在命令窗口中键入文件名回车即可；而函数文件是一条以function语句作为引导。

即文件的第一行为function[返回参数1，返回参数2，…]=函数名(输入参数1，输入参数2，…)。

这一行的有无是区分命令文件与函数文件的重要标志。

函数文件可以接受输入变量，还可以返回输出变量，执行时需在命令窗口中以固定格式调用函数方可。

习题22-1.编写程序，建立向量N=[1,2,3,4,5]，然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答：>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^22-2从键盘输入一个3位数的整数，将它反向输出。

如输入639，输出936。

输入一个百分制成绩，要求输出成绩等级A、B、C、D、E。

其中90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下为E。

要求：(1)分别用if语句和switch语句实现。

(2)输入百分制成绩后要判断该成绩的合理性，对不合理的成绩应输出出错信息。

第一章习题1. 序列满足递推关系，取及试分别计算，从而说明递推公式对于计算是不稳定的。

n1 1 0.01 0.00012 0.01 0.0001 0.0000013 0.0001 0.000001 0.000000014 0.000001 0.0000000110-105 0.00000001 10-10n1 1.000001 0.01 0.0000992 0.01 0.000099 -0.000099013 0.000099 -0.00009901-0.010000994 -0.00009901 -0.01000099-1.00015 -0.01000099-1.0001初始相差不大，而却相差那么远，计算是不稳定的。

2. 取y0=28，按递推公式，去计算y100，若取（五位有效数字），试问计算y100将有多大误差？y100中尚留有几位有效数字？解：每递推一次有误差因此，尚留有二位有效数字。

3．函数，求f(30)的值。

若开方用六位函数表，问求对数时误差有多大？若改用另一等价公式计算，求对数时误差有多大？设z=ln(30-y)，，y*， |E(y)| 10-4z*=ln(30-y*)=ln(0.0167)=-4.09235若改用等价公式设z=-ln(30+y)，，y*， |E(y)|⨯10-4z*=-ln(30+y*)=-ln(59.9833)=-4.094074．下列各数都按有效数字给出，试估计f的绝对误差限和相对误差限。

1)f=sin[(3.14)(2.685)]设f=sin xyx*=3.14, E(x)⨯10-2, y*=2.685, E(y)⨯10-3,sin(x*y*)=0.838147484, cos(x*y*)=-0.545443667⨯(-0.5454) ⨯⨯10-2+3.14(-0.5454) ⨯⨯10-3|⨯10-2⨯10-2|E r(f)| ⨯10-2⨯10-2<10-22)f=(1.56)设f = x y ,x*=1.56, E(x)⨯10-2, y*=3.414, E(y)⨯10-3,⨯⨯⨯10-2⨯⨯⨯10-3|⨯⨯⨯10-2⨯⨯⨯10-3|=0.051|E r(f)| =0.01125．计算，利用下列等式计算，哪一个得到的结果最好，为什么？6．下列各式怎样计算才能减少误差？7. 求方程x2-56x+1=0的二个根，问要使它们具有四位有效数字，至少要取几位有效数字？如果利用伟达定理， 又该取几位有效数字呢？解一:若要取到四位有效数字,如果利用伟达定理,解二:由定理二,欲使x1,x2有四位有效数字,必须使由定理一知，∆至少要取7位有效数字。