变压器外特性与效率特性
- 格式:doc
- 大小:86.50 KB
- 文档页数:4




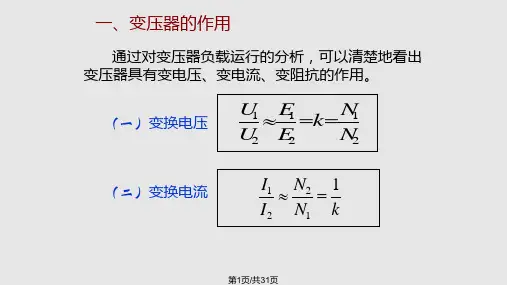


一、变压器的运行特征变压器的运行特征主要有外特征与效率特性,而表征变压器运行性能的主要指标则有电压变化率和效率。
1、电压变化率1)外特性变压器一次侧接上额定电压,二次侧开路时,二次侧空载电压就等于二次侧额定电压,外特性是指一次侧加额定电压,负载功率因数cosφ2一定时,二次侧端电压随负载电流变化的关系,即U2=f (I2)。
变压器在纯电阻和感性负载时,外特性是下降的,而客性负载时可能是上翘的。
2)电压变化率负载电流变化,变压器副边端电压将随着发生变化。
电压调整率是变压器负载时副边端电压变化程度的一种程度。
假定变压器原边接电源电压,副边开路时的端电压为额定值,当副边接入负载后,即使原来电压保持不变,副边端电压不再是额定值,原边电压保持为额定值,负载功率因数为常数,空载和负载的副边端电压之差与副边额定电压的比值,即电压变化的标么值称为电压变化率,用⊿U*表示即⊿U*=(U20-U2)/U2N式中U20—副边空载电压U2—时的副边端电压由于副边空载端电压U20等于副边额定电压U2N,经过折算后,公式1可写成⊿U*=(U20-U2)/U2N=(U'2N-U'2)/U'2N=(U10-U'2)/U1N电压变化率是变压器的主要性能指标之一,负载电流变化时,副边端电压变化的原因,是变压器内部存在电阻和漏抗而引起内部电压降。
副边电压的变化程度,即⊿U*的大小,不仅同变压器本身的阻抗有关,而且与负载的大小和性能有关。
综合上述,负载为感性时,φ2角为正值,故电压变化率为正值,即负载时的副边电压恒比空载电压低;负载为容性,φ2角为负值,故电压变化率有可能为负值,亦即负载时的副边电压可能高于空载电压。
为了保证供电电压的质量,尽可能保持副边电压的稳定,这就需要进行调压。
在电力系统中调压的方法很多,例如调节发电机出口电压,用同步调相机,在负载端并联电容器等。
但采用最多、最普遍的还是变压器调压。

第8章变压器重点变压器的基本结构、工作原理、功能与外特性和一些特殊变压器。
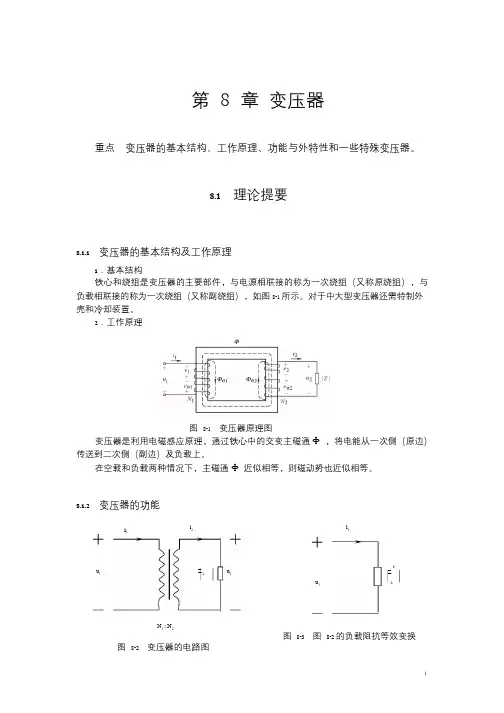
8.1 理论提要8.1.1 变压器的基本结构及工作原理1.基本结构铁心和绕组是变压器的主要部件,与电源相联接的称为一次绕组(又称原绕组),与负载相联接的称为一次绕组(又称副绕组),如图8-1 所示。
对于中大型变压器还需特制外壳和冷却装置。
2.工作原理图8-1 变压器原理图变压器是利用电磁感应原理,通过铁心中的交变主磁通Φ,将电能从一次侧(原边)传送到二次侧(副边)及负载上。
在空载和负载两种情况下,主磁通Φ近似相等,则磁动势也近似相等。
8.1.2 变压器的功能i1i2i1u 1 Z L u2Z′u1 LN1 : N2图8-3 图8-2 的负载阻抗等效变换图8-2 变压器的电路图11.电压变换U=N=1 1U N2 2K即:变压器一次、二次绕组的感应电动势与其匝数成正比,电路如图8-2 所示。
当变压器的变比K>1 时,变压器功能为降压变压器;当K<1 时,变压器功能为升压变压器。
2.电流变换I N 11 =2 =I N K2 1即:变压器一次、二次绕组的电流之比近似等于它们的匝数比的倒数,电路如图8-2 所示。
3.阻抗变换Z′=K2 ZL L其等效变换电路如图8-3 所示。
利用阻抗变换关系式,可使负载从电源上获取最大功率,即使其等效阻抗与电源内阻抗相等,又称为阻抗匹配。
4.变压器的损耗与效率η=P 2 P 1式中,P为变压器的输出功率,2 P为输入功率,η为效率。
1P、1 P与损耗的关系2P=P+P+P1 2 cu Fe其中:铁损耗P Fe 是不变损耗,在U1 和f一定时,不随负载大小的变化而变化;铜损耗P Cu 是可变损耗,其大小正比于电流的平方。
变压器的功率损耗小,效率高,通常为95%以上。
5.额定容量单相变压器S N =U I≈U I2N 2N 1N 1N当变压器额定运行时,二次(副边)电流为额定电流,二次电压U<U。


变压器外特性和电压变化率 1. 变压器的外特性变压器的外特性是指一次侧电压为额定值U 1N ,负载功率因数cos φ2一定时,二次侧端电压U 2随负载电流I 2变化的关系曲线,即U 2=f (I 2),如图1所示。
在负载运行时,由于变压器内部存在阻抗和漏抗,当负载电流流过时,变压器内部将产生阻抗压降,使二次端电压随负载的变化而变化。
图1-2-6所示为不同负载性质时变压器的外特性曲线。
由图可知,当负载容性时,外特性是上翘的;而负载感性时,外特性是下降的。
也就是说容性电流有助磁作用,使U 2上升;而感性电流有去磁作用,使U 2下降。
变压器二次电压的大小不仅与负载电流的大小有关,还与负载的功率因数有关。
图1 变压器的外特性曲线图因此,在变压器输入电压U 1不变时,影响外特性的因素是Zs l 、Zs 2及cos 2ϕ。
为了使各种不同容量和电压的变压器的外特性可以进行比较,在图1-2-6中坐标都用相对值U 2/U 2N 、I 2/I 2N 表示,这种值也称为标么值。
2. 电压变化率(电压调整率)变压器二次侧输出电压随负载而变化的程度用电压变化率ΔU%示。
所谓电压变化率,是指变压器一次绕组加额定电压,负载的功率因数一定,空载与额定负载时二次侧端电压之差(U 2N -U 2)与额定电压U 2N 的比值,,通常可以表示为:100%222⨯-=∆N N U U U U %=1002⨯∆NU U % 式中 U 2N ——变压器二次侧输出额定电压(即二次侧空载电压U 02)U 2——变压器二次侧额定电流时的输出电压。
电压变化率△U%是表征变压器运行性能的重要指标之一,它的大小与负载大小、性质及变压器的本身参数有关,反映了供电电压的稳定性。
一般电力变压器,当cos 2ϕ≈1时,%U ∆≈2%~3%,当cos 2ϕ≈0.8时,%U ∆≈4%~6%,可见提高二次侧负载功率因数cos 2ϕ,还能提高二次侧电压的稳定性。
一般情况下照明电源电压波动不超过±5%,动力电源电压波动不超过+10%~—5%。
湖南省技工学校
理论教学教案
教师姓名:
注:教案首页,教案用纸由学校另行准备湖南省劳动厅编制
益阳高级技工学校
图1.12 变压器的外特性
电容性负载:U 2随I 2的增大而增大(容性负载减小了无功电流分量);电阻和电感性负载:U 2随I 2的增大而减小。
变化程度用电压变化率来表示。
定义:100%100%22
22220N
N N U U U U U U U -=-=
∆
益阳高级技工学校
益阳高级技工学校
图1.13 变压器的效率特性 二、变压器的阻抗变换
变压器一次侧接交流电源,对电源来说是一个负载。
抗可用输入电压、输入电流来计算,即变压器的输入阻抗为11
I U ,而变压器的二次侧输出又接了负载,电压、在Z2=
2
2
I U =Z fz 关系。
可以看出经过变压器把要变压器直接把Z 2接到电源上,两者是完全不一样的,这里变压器起到改变阻抗的作用,把Z 2变成Z 1可以在 变换公式
这说明负载Z 2经过变压器以后阻抗扩大了抗Z 2的大小,要把它变成另一个一定大小的阻抗变压器,该变压器的变比K=21/Z Z
在电子线路中,这种阻抗变换很常用,如扩音设备中扬声器的.阻抗很小(4~16),直接接到功放的输出,则扬声器得到的功率很小,
益阳高级技工学校。
变压器的主要参数有哪些?分别代表什么含义
变压器的主要参数有电压比、频率特性、额定功率和效率等。
(一)电压比n变压器的电压比n与一次、二次绕组的匝数和电压之间的关系如下:n=V1/V2=N1/N2
式中N1为变压器一次(初级)绕组,N2为二次(次级)绕组,V1为一次绕组两端的电压,V2是二次绕组两端的电压。
升压变压器的电压比n小于1,降压变压器的电压比n大于1,隔离变压器的电压比等于1。
(二)额定功率P此参数一般用于电源变压器。
它是指电源变压器在规定的工作频率和电压下,能长期工作而不超过限定温度时的输出功率。
变压器的额定功率与铁心截面积、漆包线直径等有关。
变压器的铁心截面积大、漆包线直径粗,其输出功率也大。
(三)频率特性频率特性是指变压器有一定有工作频率范围,不同工作频率范围的变压器,一般不能互换使用。
因为变压器有其频率范围以外工作时,会出现工作时温度升高或不能正常工作等现象。
(四)效率效率是指在额定负载时,变压器输出功率与输入功率的比值。
该值与变压器的输出功率成正比,即变压器的输出功率越大,效率也越高;变压器的输出功率越小,效率也越低。
变压器的效率值一般在60%~100%之间。
工厂供配电知识点变压器的外特性及电压调节变压器是工厂供配电系统中重要的设备之一,主要用于电能的传输和变换。
在工厂供配电的过程中,变压器的外特性及电压调节是需要了解和掌握的知识点。
下面将详细介绍变压器的外特性和电压调节。
一、变压器的外特性1.开路特性:变压器的开路特性是指在载流量为零时,变压器二次侧开路电压与一次侧电压的关系。
开路特性可通过实验方法测得,通常以开路试验来确定。
2.短路特性:变压器的短路特性是指当变压器的一次侧短路,二次侧接负载时,变压器的电压与电流之间的关系。
短路特性可通过实验方法测得,通常以短路试验来确定。
3.额定容量:变压器的额定容量是指变压器可连续工作的最大容量,也是变压器选择和设计的重要参数。
额定容量与变压器的输出功率直接相关。
4.空载损耗:变压器的空载损耗是指变压器在无负载运行时的损耗,包括铁心损耗和电流损耗。
5.负载损耗:变压器的负载损耗是指变压器在负载运行时的损耗,主要由铜损耗和铁心损耗组成。
二、电压调节电压调节是指在负载变动或系统电压波动时,变压器能够稳定输出额定的电压。
电压调节主要分为静态调压和动态调压两种。
1.静态调压:静态调压是指在变压器负载不变的情况下,通过调节一次侧电压来实现输出电压的稳定。
静态调压主要通过变压器的变比来实现,通过调节变比,可以改变变压器的输出电压。
2.动态调压:动态调压是指在变压器负载变动或系统电压波动的情况下,通过自动控制来调整变压器的输出电压,使其保持稳定。
动态调压主要通过自动稳压器来实现,自动稳压器根据输出电压的变化,调节变压器的变比或输入电压,以实现电压的稳定。
电压调节的目的是为了保持变压器的输出电压稳定,以保证工厂供配电系统正常运行。
在实际应用中,需要根据变压器的负载情况和系统电压波动情况进行合理的电压调节设计,以实现稳定的供电。
综上所述,变压器的外特性及电压调节是工厂供配电中重要的知识点。
了解变压器的外特性,可以帮助正确选择和设计变压器,并保证变压器的正常运行。
一、变压器的外特性及电压变化率
变压器空载运行时,若一次绕组电压U
1不变,则二次绕组电压U
2
也是不变的。
变压器加上负载之后,随着负载电流I
2的增加,I
2
在二次绕组内部的阻抗压降也
会增加,使二次绕组输出的电压U
2
随之发生变化。
另一方面,由于一次绕组电
流I
1随U
2
增加,因此I
2
增加时,使一次绕组漏阻抗上的压降也增加,一次绕组
电动势E
1和二次绕组电动势E
2
也会有所下降,这也会影响二次绕组的输出电压
U 2。
变压器的外特性是用来描述输出电压U
2
随负载电流I
2
的变化而变化的情况。
当一次绕组电压U
1和负载的功率因数cosφ
2
一定时,二次绕组电压U
2
与负载电
流I
2
的关系,称为变压器的外特性。
它可以通过实验求得。
功率因数不同时的
几条外特性绘于图2—17中,可以看出,当cosφ
2=1时,U
2
随I
2
的增加而下降
得并不多;当cosφ
2降低时,即在感性负载时,U
2
随I
2
增加而下降的程度加大,
这是因为滞后的无功电流对变压器磁路中的主磁通的去磁作用更为显著,而使
E 1和E
2
有所下降的缘故;但当cosφ
2
为负值时,即在容性负载时,超前的无功
电流有助磁作用,主磁通会有所增加,E
1和E
2
亦相应加大,使得U
2
会随I
2
的增
加而提高。
以上叙述表明,负载的功率因数对变压器外特性的影响是很大的。
图2-17 变压器外特性
在图2—17中,纵坐标用U
2/U
2N
之值表示,而横坐标用I
2
/I
2N
表示,使得在坐
标轴上的数值都在0~1之间,或稍大于1,这样做是为了便于不同容量和不同电压的变压器相互比较。
一般情况下,变压器的负载大多数是感性负载,因而当负载增加时,输出电压U
2
总是下降的,其下降的程度常用电压变化率来描述。
当变压器从空载到额定负
载(I
2=I
2N
)运行时,二次绕组输出电压的变化值ΔU与空载电压(额定电压)
U
2N
之比的百分值就称为变压器的电压变化率,用ΔU%来表示。
式中,U
2N 为变压器空载时二次绕组的电压(称为额定电压);U
2
为二次绕组输出
额定电流时的电压。
电压变化率反映了供电电压的稳定性,是变压器的一个重要性能指标。
ΔU%越小,说明变压器二次绕组输出的电压越稳定,因此要求变压器的ΔU%越小越好。
常用的电力变压器从空载到满载,电压变化率约为3%~5%。
例2—4:某台供电电力变压器将U
1N
=10000V的高压降压后对负载供电,要求该
变压器在额定负载下的输出电压为U
2
=380V,该变压器的电压变化率ΔU%=5%,
求该变压器二次绕组的额定电压U
2N
及变比K。
这样,就能理解在电力变压器铭牌中为什么给额定线电压为380V的负载供电时,变压器二次绕组的额定电压不是380V,而是400V。
二、变压器的损耗及效率
变压器从电源输入的有功功率P
1和向负载输出的有功功率P
2
可分别用下式计算
P
1
=U
1
I
1
COSφ
1
P
2
=U
2
I
2
COSφ
2
两者之差为变压器的损耗ΔP,它包括铜损耗P
Cu 和铁损耗P
Fe
两部分,即
ΔP=P
Cu +P
Fe
1.铁损耗P
Fe
变压器的铁损耗包括基本铁损耗和附加铁损耗两部分。
基本铁损耗包括铁心中的磁滞损耗和涡流损耗,它决定于铁心中的磁通密度的大小、磁通交变的频率和硅钢片的质量等。
附加损耗则包括铁心叠片间因绝缘损伤而产生的局部涡流损耗、
主磁通在变压器铁心以外的结构部件中引起的涡流损耗等,附加损耗约为基本损耗的15%~20%左右。
变压器的铁损耗与一次绕组上所加的电源电压大小有关,而与负载电流的大小无关。
当电源电压一定时,铁心中的磁通基本不变,故铁损耗也就基本不变,因此铁损耗又称“不变损耗”。
2.铜损耗P
Cu
变压器的铜损耗也分为基本铜损耗和附加铜损耗两部分。
基本铜损耗是由电流在一次、二次绕组电阻上产生的损耗,而附加铜损耗是指由漏磁通产生的集肤效应使电流在导体内分布不均匀而产生的额外损耗。
附加铜损耗约占基本铜损耗的3%~20%。
在变压器中铜损耗与负载电流的平方成正比,所以铜损耗又称为“可变损耗”
3.效率
变压器的输出功率P
2与输入功率P
1
之比称为变压器的效率η,即
由于变压器没有旋转的部件,不像电机那样有机械损耗存在,因此变压器的效率一般都比较高,中小型电力变压器效率在95%以上,大型电力变压器效率可达99%以上。
例2-5:S9-500/10低损耗三相电力变压器额定容量500kV·A,设功率因素为
1,二次电压U
2N =400V,铁损耗P
Fe
=0.98KW,额定负载时铜损耗=P
Cu
=4.1kW,求二
次额定电流I
2N
及变压器效率η。
前面已经讲过降低变压器本身的损耗,提高其效率是供电系统中一个极为重要的课题,世界各国都在大力研究高效节能变压器,其主要途径:一是采用低损耗的
冷轧硅钢片来制作铁心,例如容量相同的两台电力变压器,用热轧硅钢片制作铁心的SJl—1000/10变压器铁损耗约为4440W。
用冷轧硅钢片制作铁心的
S7—1000/10变压器铁损耗仅为1700W。
后者比前者每小时可减少2.7kW·h的损耗,仅此一项每年可节电23 652kW·h。
由此可见,为什么我国要强制推行使用低损耗变压器。
二是减小铜损耗,如果能用超导材料来制作变压器绕组,则可使其电阻为零,铜损耗也就不存在了。
世界上许多国家正在致力于该项研究,目前已有330kV单相超导变压器问世,其体积比普通变压器要小70%左右,损耗可降低50%。
4.效率特性
变压器在不同的负载电流I
2时,输出功率P
2
及铜损耗P
Cu
都在变化,因此变压器
的效率η也随负载电流I
2
的变化而变化,其变化规律通常用变压器的效率特性曲线来表示,如图2—18所示,图中称为负载系数。
通过数学分析可知:当变压器的不变损耗等于可变损耗时,变压器的效率最高,通常变压器的最高效率位于β=0.5∽0.6之间。
图2-18 变压器效率曲线。