有关晶胞计算

有关晶体的各类计算晶体是由原子、分子或离子按照一定的规则排列组成的固体物质。

晶体的结构和性质可以通过各种计算方法进行研究和预测。

本文将介绍晶体的各类计算方法，包括晶胞参数计算、电子结构计算和晶格动力学计算等。

一、晶胞参数计算方法晶胞参数是描述晶体结构的基本参数，包括晶胞长度、晶胞角度等。

晶胞参数计算方法主要分为实验方法和理论方法两类。

1.实验方法：通过实验手段确定晶胞参数，包括X射线衍射、中子衍射、电子衍射等技术。

这些技术可以通过测量晶体的衍射角度和强度，来反推晶体的晶胞参数。

例如，通过X射线衍射技术可以得到晶胞的长度和角度信息，然后利用几何学和晶体学理论进行分析计算。

2. 理论方法：通过理论计算手段预测晶胞参数，包括密度泛函理论（DFT）、分子力学方法、量子力学方法等。

这些方法可以从晶胞的能量最小化和最优结构寻找中确定晶胞参数。

密度泛函理论是一种基于电子密度的计算方法，可以通过求解Kohn-Sham方程得到晶体的基态电子结构和晶胞参数。

分子力学方法则将晶体中的原子看作经典力学粒子，通过经典力学力场计算得到晶体的能量和结构。

二、电子结构计算方法电子结构是指描述晶体中电子的运动状态和能量分布的理论框架。

电子结构计算方法可以通过计算分子轨道、能带结构和态密度等参数来描述晶体的电子性质。

1. 密度泛函理论（DFT）：DFT是一种基于电子密度的计算方法，可以精确计算晶胞中的电子结构和物理性质。

DFT方法通过求解Kohn-Sham 方程，得到晶体的基态电子密度和能量。

然后可以通过电子密度计算组态关联能、原子电荷分布、态密度和光谱等电子性质指标。

2. 分子轨道方法：分子轨道方法将晶体中的电子看作在分子轨道上运动，通过求解电子的分子轨道波函数，可以得到晶体的基态电子结构和反应性。

常用的分子轨道方法有Hückel方法、扩展Hückel方法、Hartree-Fock方法等。

这些方法对于大尺寸的晶体模型计算较耗时，但适用于分子结构的预测和反应物和产物的性质计算。

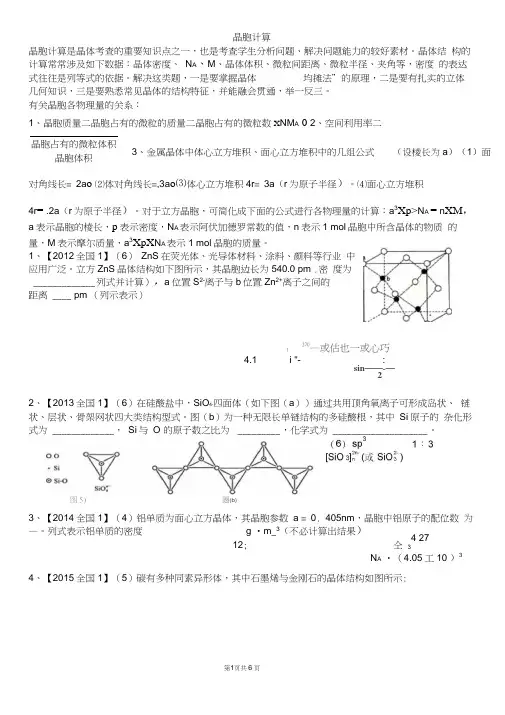
第1页共6页晶胞计算晶胞计算是晶体考查的重要知识点之一，也是考查学生分析问题、解决问题能力的较好素材。

晶体结 构的计算常常涉及如下数据：晶体密度、 N A 、M 、晶体体积、微粒间距离、微粒半径、夹角等，密度 的表达式往往是列等式的依据。

解决这类题，一是要掌握晶体 均摊法”的原理，二是要有扎实的立体 几何知识，三是要熟悉常见晶体的结构特征，并能融会贯通，举一反三。

有关晶胞各物理量的关系：1、晶胞质量二晶胞占有的微粒的质量二晶胞占有的微粒数X NM A 02、空间利用率二对角线长= 2a o ⑵体对角线长=,3a o ⑶体心立方堆积4r = 3a （r 为原子半径）。

⑷面心立方堆积4r = .2a （r 为原子半径）。

对于立方晶胞，可简化成下面的公式进行各物理量的计算：a 3Xp>N A = n XM ， a 表示晶胞的棱长，p 表示密度，N A 表示阿伏加德罗常数的值，n 表示1 mol 晶胞中所含晶体的物质 的量，M 表示摩尔质量，a 3XpX N A 表示1 mol 晶胞的质量。

1、【2012全国1】（6） ZnS 在荧光体、光导体材料、涂料、颜料等行业 中应用广泛。

立方ZnS 晶体结构如下图所示，其晶胞边长为540.0 pm .密 度为 _____________ 列式并计算），a 位置S 2-离子与b 位置Zn 2+离子之间的 距离 ____ pm （列示表示）f270—或估也一或心巧4.1 i "- :sin ——-—22、【2013全国1】（6）在硅酸盐中，SiO 4-四面体（如下图（a ））通过共用顶角氧离子可形成岛状、 链状、层状、骨架网状四大类结构型式。

图（b ）为一种无限长单链结构的多硅酸根，其中 Si 原子的 杂化形式为 _____________ ， Si 与 O 的原子数之比为 _________ ，化学式为 ____________________ 。

涉及晶胞的有关计算晶胞作为晶体结构的基本单元，具有“无隙并置”，可平移的特征。

通过对晶胞上占有的粒子数、晶胞体积的计算，结合阿伏伽德罗常数可以把微观的晶胞和宏观的物质的有关性质密度、摩尔质量联系起来。

从99年高考出现NiO晶胞与晶体密度关系计算以来，涉及晶胞的计算在高中化学教学中一直被作为一个重点，而且在计算的设计上变化层出。

例：晶体具有规则的几何外形，晶体中最基本的重复单元称为晶胞。

NaCl晶体结构如图所示。

已知FexO晶体晶胞结构为NaCl型，由于晶体缺陷，x值小于1。

测知FexO晶体密度ρ=5.71g/cm3，晶胞边长a = 4.28×10－10m。

（铁相对原子质量为55.9，氧相对原子质量为16）求：（1）FexO中x值（精确至0.01）为_____________。

（2）晶体中的Fe分别为Fe2＋、Fe3＋，在Fe2＋和Fe3＋的总数中，Fe2＋所占分数（用小数表示，精确至0.001）为___________。

（3）此晶体化学式为___________。

解析：要计算x的值实际就是计算Fe x O的摩尔质量。

假定有1molFe x O晶体，求出1mol晶体质量即可解决问题。

题目条件中有晶体密度，如果求出1mol晶体的体积，体积乘以密度就是质量。

这样问题就转化为求1mol晶体的体积了。

1mol Fe x O晶体含有N A个O2- ,一个晶胞上占有4个O2-,所以1mol晶体含有N A/4个晶胞。

每个晶胞的体积V = a 3 = (4.28×10－8cm)3，因此1mol晶体的体积就是N A ×(4.28×10－8cm)3/4。

1mol晶体质量为m =ρ.(NA/4).V = 5.71g/cm3×(NA/4)×(4.28×10－8cm)3 = 67.4g。

x =(67.4－16)/56 = 0.92 。

（3）小题的答案就可以表示为Fe0.92O 。

晶胞的有关计算：体积、微粒数、晶体密度一、如何利用晶胞参数计算晶胞体积？平行六面体的几何特征可用边长关系和夹角关系确定。

布拉维晶胞的边长与夹角叫做晶胞参数。

共有7种不同几何特征的三维晶胞，称为布拉维系，它们的名称、英文名称、符号及几何特征如下：立方cubic(c)a=b=c,α=β=γ=90°,(只有一个晶胞参数a)四方tetragonal(t)a=b≠c,α=β=γ=90°,(有2个晶胞参数a 和c)六方hexagonal(h)a=b≠c,α=β=90°,γ=120°,(有2个晶胞参数a 和c)正交orthorhombic(o)a≠b≠c,α=γ=90°,(有3个晶胞参数a,b 和c)单斜monoclinic(m)a≠b≠c,α=γ=90°,β≠90°,(有4个晶胞参数a,b,c 和β) 三斜anorthic(a)a≠b≠c,α≠β≠γ,(有6个晶胞参数a,b,c,α,β和γ)菱方rhombohedral(R)a=b=c,α=β=γ≠90°,(有2个晶胞参数a 和α)六方a^2Xcsin120正交V=abc单斜V=abcsin β三斜V=abc(1-cos2α-cos2β-cos2γ+2cos αcos βcos γ)菱方V=a^3(1-3cos2α+2(cos α)^3)二、均摊法---计算晶胞中的粒子数位于晶胞顶点的微粒,实际提供给晶胞的只有1/8;位于晶胞棱边的微粒,实际提供给晶胞的只有1/4;位于晶胞面心的微粒,实际提供给晶胞的只有1/2;位于晶胞中心的微粒,实际提供给晶胞的只有1.三、晶胞的密度计算1） 利用晶胞参数可计算晶胞体积(V)，根据相对分子质量(M)、晶胞中粒子数(Z)和阿伏伽德罗NA ，可计算晶体的密度ρ：V N MZ A =ρ。

晶胞的计算一、晶胞在高考中的地位分析：2008、2009年新课标，未对晶胞的计算进行考查；2010年新课标：37（4），一空，化学式的计算；2011年新课标：37（5），三空，晶胞中原子个数及密度的计算；2012年新课标：37（6），两空，晶胞密度、离子距离的计算。

二、常见的晶胞计算题：第一类：金属堆积方式的简单计算（空间利用率和密度）[选三P76] 晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m＝10dm＝102 cm＝103 mm＝106 um＝109 nm＝1012 pm①简单立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：②体心立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：③面心立方最密堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：再假设该金属的摩尔质量为Mg/mol，N A为阿伏伽德罗常数的数值，试计算该晶胞的密度：【总结】必须掌握的常见晶胞及晶体结构分子晶体：干冰、冰晶胞图形、晶胞组成特点；原子晶体：金刚石（晶体硅）、二氧化硅晶胞组成特点、边长（体积、密度、原子最近距离）的计算方式；金属晶体：四种堆积方式的名称、图形、代表金属、边长（体积、密度、原子最近距离）的计算方式；离子晶体：NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长（体积、密度、原子最近距离）的计算方式。

【练习】中学化学教材中展示了NaCl晶体结构，它向三维空间延伸得到完美晶体。

NiO(氧化镍)晶体的结构与NaCl 相同，Ni2+与最临近O2-的核间距离为 a cm，计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。

(2)天然和绝大部分人工制备的晶体都存在各种缺陷，例如在某氧化镍晶体中就存在如图所示的缺陷：一个Ni2+空缺，另有两个Ni2+被两个Ni3+所取代。

其结果为晶体仍呈电中性，但化合物中Ni 和O的比值却发生了变化。

晶胞的计算一、晶胞在高考中的地位分析：2008、2009年新课标，未对晶胞的计算进行考查；2010年新课标：37（4），一空，化学式的计算；2011年新课标：37（5），三空，晶胞中原子个数及密度的计算；2012年新课标：37（6），两空，晶胞密度、离子距离的计算。

二、常见的晶胞计算题：第一类：金属堆积方式的简单计算（空间利用率和密度）[选三P76]晶胞密度 =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100%【注】1m＝10dm＝102 cm＝103 mm＝106 um＝109 nm＝1012 pm①简单立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：②体心立方堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：③面心立方最密堆积：假设球的半径为r cm，则该堆积方式的空间利用率为：再假设该金属的摩尔质量为Mg/mol，N A为阿伏伽德罗常数的数值，试计算该晶胞的密度：【总结】必须掌握的常见晶胞及晶体结构分子晶体：干冰、冰晶胞图形、晶胞组成特点；原子晶体：金刚石（晶体硅）、二氧化硅晶胞组成特点、边长（体积、密度、原子最近距离）的计算方式；金属晶体：四种堆积方式的名称、图形、代表金属、边长（体积、密度、原子最近距离）的计算方式；离子晶体：NaCl、CsCl、CaF2晶胞图形、晶胞组成、边长（体积、密度、原子最近距离）的计算方式。

【练习】中学化学教材中展示了NaCl晶体结构，它向三维空间延伸得到完美晶体。

NiO(氧化镍)晶体的结构与NaCl 相同，Ni2+与最临近O2-的核间距离为a cm，计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g/mol)。

(2)天然和绝大部分人工制备的晶体都存在各种缺陷，例如在某氧化镍晶体中就存在如图所示的缺陷：一个Ni2+空缺，另有两个Ni2+被两个Ni3+所取代。

其结果为晶体仍呈电中性，但化合物中Ni 和O的比值却发生了变化。

有关晶胞的计算
1.利用晶胞参数可计算晶胞体积(V)，根据相对分子质量(M)、晶胞中粒子数(Z)和阿伏伽德罗常数NA，可计算晶体的密度：
（1）简单立方
（2）体心立方
（3）面心立方
（4）金刚石型晶胞
球体积
空间利用率 = 100%
晶胞体积
晶体中原子空间利用率的计算步骤：
（1）计算晶胞中的微粒数（2）计算晶胞的体积
实例：
（1）简单立方
在立方体顶点的微粒为8个晶胞共享，微粒数为：8×1/8 = 1
（2）体心立方
在立方体顶点的微粒为8个晶胞共享，处于体心的金属原子全部属于该晶胞。

1个晶胞所含微粒数为：8×1/8 + 1 = 2
晶胞的对角线为C=4R
V
N
MZ
A
=
ρ
（3）面心立方
在立方体顶点的微粒为8个晶胞共有，在面心的为2个晶胞共有。

1个晶胞所含微粒数为：8×1/8 + 6×1/2 = 4
空间占有率为
（4）金刚石型晶胞
金刚石晶胞是面心立方堆完之后还在四个四面体里有原子
原子半径和晶胞边长的契合点在于体对角线上连着排了四个原子，所以是8个半径等于根号3个边长
所以a：r=8：根号3。

例谈有关晶胞的计算类型与方法晶胞是微小的三维结构，由像水晶一样的互相连接的各种原子构成，它们可以存储和传递信息，并帮助我们更好地理解世界。

此外，晶胞的计算功能可以用于支持研究和应用。

近年来，随着计算机科学与技术的发展，晶体计算类型与方法在科学和工程领域得到越来越多的关注。

一、晶体计算类型晶体计算是指使用原子加成等晶体力学的方法来研究微细的物理和化学系统的计算方法，晶体计算类型可以分为两大类：传统的晶体计算和新型的晶体计算。

1、传统的晶体计算传统的晶体计算通常采用分子动力学，量子化学和其他类似技术来描述晶体结构，以及晶体与环境之间的相互作用。

可视化技术也被用于模拟晶体结构，以及对晶体结构进行力学分析。

2、新型的晶体计算新型的晶体计算利用高性能计算和现代网络技术，将大规模非结构化数据和高效率算法结合，从而实现更大范围的晶体计算。

目前，这种新型的晶体计算正在迅速发展，不仅在科学与工程领域有着广泛的应用，同时也可用于解决相关技术问题。

二、晶胞计算方法晶胞计算主要分为三种方法：第一种是基于现实的结构模拟，例如分子动力学、量子化学和原子加成等；第二种是基于经典物理学方法，例如电阻网络模型；第三种是基于数学模型对系统进行建模，例如计算力学模型，以及诸如熵、温度、压力和化学势等物理参数的模型。

1、基于现实的结构模拟现实的结构模拟是指使用分子动力学、量子化学和其他力学模型，去实现晶胞内部细胞结构的准确模拟；通过使用计算机模拟系统，可以实时地模拟晶胞中各种参数，并准确地预测该晶胞中分子和原子结构的运动和变化趋势。

2、基于经典物理学方法经典物理学方法是指使用电阻网络模型进行计算，这种模型可以基于晶胞内部的拓扑结构，以及晶胞与外界环境的相互作用，来逼近晶胞的特性。

3、基于数学模型的晶胞计算数学模型的晶胞计算是指利用计算力学模型，结合各种物理参数，如熵、温度、压力和化学势，来构建晶胞结构的一种计算方式。

该方法可以准确地描述晶胞在环境条件下的各种变化，从而更好地理解晶胞的功能。