实验地图投影的判别

地图投影实验报告现代地图学A 实验报告实验名称：专题地图制作班级：测绘122 姓名：苏红飞实验地点：测绘楼307 实验时间： 2019-12-02测绘工程学院测绘工程系实验一地图投影一、实验目的与要求1. 学会MapInfo 的最基本操作，如表、工作空间、图层等的操作。

2. 掌握有关高斯－克吕格投影的知识。

3. 学会根据地图上不同经纬网形态识别不同的投影类型。

二、实验步骤（一）掌握MapInfo 中地图投影的操作过程。

（二）绘制武汉市所在地区的高斯—克吕格投影6度带经纬网和方里网，绘图范围：东西范围由武汉市所在投影带决定，南北范围：北纬25o —35o 。

经线线距1，纬线线距1o 。

1、打开MapInfo ，出现如图1所示的对话框，点击ok 键。

图 12、如图2-1所示，在File 选项中选中open 点击，打开“实验素材”（图2-2）。

图2-1 图2-23、再依次打开CHINA.TAB 、CHINCAP.TAB 、PROVINCE.TAB ，打开后如图3所示。

图34、点击Layer Control，如图4-1所示。

在Tools 选项中单击Tool Manger...出现下图4-3中所示的对话框，选中Coordinate Extractor，将它后面的两个小框打钩。

图4-1 图4-2图4-35、在Tools 菜单中单击Coordinate Extractor中的Extract Coordinates...选项出现如图5-2所示的对话框，在table name 一栏中选择CHINCAPS ，然后点击ok 出现如图5-3所示的对话框，选择continue ，即可看见如图5-4所示的窗口，在上面找到并记下武汉的地理坐标。

图5-1图5-2 图5-3图5-46、新建一个空白表，出现如图6-1所示的对话框，单击Create ，然后出现图6-2所示对话框，在Name 框中填写ID ，而且在type 选项中选择Integer ，如图6-3所示。

Mapgis实验报告范文实验员：胡蝶班级学号：1002601时间：2022.4指导教师:周青山老师实验名称：地图投影的制作、判别和变换实验地点：湖南城市学院实验楼418实验原理：mapgi、envi软件的基本操作方法实验材料和条件：中国地图、世界地图；计算机，铅笔；MAPGIS软件等。

实验目的：1、巩固学过的地图投影知识；2、掌握地图投影判别的方法、步骤；3、为正确使用地图投影奠定理论基础。

实验内容与步骤：1、地图投影类型回顾1.1、几何投影中、小比例尺地图投影：正轴圆锥、圆柱、方位投影；横、斜轴方位投影；大、中比例尺地图投影：高斯投影、UTM投影。

1.2、条件投影等积锥投影；等角锥投影；等距柱投影。

2、投影判别的一般原则2.1、制图区域的范围、形状和地理位置区域范围大尺度中尺度区域形状近似圆形区域南北延伸型区域两极地理位置赤道附近小尺度2.2、制图比例尺东西延伸型区域中纬度地区大、中比例尺地图，对制图几何精度要求高，制图区域范围小，宜采用高斯投影，UTM等；中、小比例尺地图概括程度高，制图范围大，多采用正轴圆锥、圆柱、方位等投影。

2.3、地图的主题和内容要求方向正确，应选择等角投影；要求面积对比正确，应选择等积投影；教学或一般参考图，要求各方面变形都不大，则应选择任意投影。

2.4、出版方式单幅图；系列图、地图集：同一图组（或系列）内投影尽可能一致，且投影种类不宜过多。

3地图投影判别的方法与步骤3.1方法1)观察法：观测地图的经纬网形状；2)量测法：经纬线方向形状变形量，3.2步骤1)根据投影判别的一般原则,并结合经纬网形状初步确定投影系统；A.经纬线形状的判别：目视并辅以量算判断。

经线形状有：直线，曲线。

纬线形状有：直线，同心圆弧，同轴圆弧，曲线B.经纬线是否直交。

2)量测中经上纬线间距变化，判定投影性质。

A.在中央经线上，找到标准点(线)的位置；圆锥投影、圆柱投影：标准切(割)纬线与中央经线的交点。

地图投影的判别和选择投影方式的依据大家知道，地图投影的类型之多，分别使用在不同的场合下，那么我们在生产中选择地图投影的依据是什么呢？应该怎样确定投影类型呢？不同的投影类型的特点及变形特点如何？带着这些问题请看本文讲解.不同类型的投影通常具有不同的经纬线特点，因此投影类型可以通过判别经纬线网的形状来确定。

在确定投影类型时，准确区分经纬线是直线与曲线、同心圆弧与同轴圆弧，是非常重要的。

一、地图投影的判别不同的投影具有不同的变形特点。

判别投影的类型和变形性质，是正确使用地图的基础。

由于大比例尺地图通常属于国家基本比例尺地形图，投影简单，易于查知，且包含的制图区域小，无论采用何种投影，变形都很小。

因此，地图投影的判别主要是针对小比例尺地图而言。

判别地图投影，一般先是根据经纬线网的形状确定投影的类型，如方位投影、圆柱投影、圆锥投影等；然后是判定投影的变形性质，如等角、等积或任意投影。

1、确定投影类型不同类型的投影通常具有不同的经纬线特点，因此投影类型可以通过判别经纬线网的形状来确定。

在确定投影类型时，准确区分经纬线是直线与曲线、同心圆弧与同轴圆弧，是非常重要的。

直线只要用直尺比量，便可确定。

判断曲线是否为圆弧，可用点迹法，即将透明纸覆盖在曲线上，在透明纸上沿曲线按一定间距定出3至6个点，然后沿曲线徐徐向一端移动透明纸，若这些点始终都不偏离此曲线，则证明此曲线是圆弧，否则就是其它曲线。

判别纬线是同心圆弧还是同轴圆弧，可量算相邻圆弧间的纬线间隔（即经线长），若处处相等，则证明这些圆弧为同心圆弧，否则便是同轴圆弧。

此外，由于正轴圆锥投影与正轴方位投影的经纬线形状有时可能完全相同，因此，在判别时，可以通过以下两种方法来区分：一是量算相邻两条经线的夹角是否与实地经差相等。

若相等则为方位投影，否则就是圆锥投影；二是分析制图区域所处的地理位置。

若制图区域在极地一带，则为正轴方位投影，若在中纬度地带，则为圆锥投影。

2、确定投影变形性质在确定了投影的类型之后，可以进一步根据经纬线网的图形特征，确定投影的变形性质。

一、实验目的本次实验旨在了解地球球面投影到平面时产生的变形，掌握地图投影的变形特征，分析不同投影方式对地图变形的影响，提高对地图投影变形的认识。

二、实验原理地球椭球面是一个不可展的曲面，而地图是一个平面。

在将地球椭球面上的经纬线网描绘成平面图形的过程中，必然会发生各种变形。

这些变形主要包括长度变形、角度变形和面积变形。

地图投影就是研究如何将地球椭球面上的经纬线网准确地描绘到平面上的方法。

三、实验材料与工具1. 地球仪2. 白纸3. 铅笔4. 剪刀5. 比例尺6. 地图投影软件（如Google Earth）四、实验步骤1. 将地球仪放置在桌面上，用铅笔在白纸上画出地球仪的大致轮廓。

2. 使用剪刀将白纸沿地球仪轮廓剪下，得到一个近似球面的平面。

3. 在地球仪上选取一个经纬度点，用铅笔在白纸上标记出该点的位置。

4. 将地球仪上的经纬线网描绘到白纸上，注意保持经纬线之间的相对位置。

5. 使用比例尺测量白纸上的经纬线长度，并与地球仪上的实际长度进行比较，分析长度变形。

6. 在白纸上选择一个点，测量该点所在经线的角度，并与地球仪上的实际角度进行比较，分析角度变形。

7. 使用地图投影软件，将地球仪上的经纬线网投影到平面地图上，比较不同投影方式下的地图变形。

五、实验结果与分析1. 长度变形在实验过程中，我们发现白纸上的经纬线长度与地球仪上的实际长度存在差异。

这是因为地球椭球面是不可展的曲面，而白纸是一个平面。

在将地球椭球面上的经纬线网描绘到白纸上时，必然会发生长度变形。

根据实验结果，我们可以发现，在地球仪的赤道附近，长度变形较小；而在两极附近，长度变形较大。

2. 角度变形实验结果表明，白纸上的经纬线角度与地球仪上的实际角度存在差异。

这是由于地球椭球面是不可展的曲面，而在将地球椭球面上的经纬线网描绘到白纸上时，角度变形不可避免。

根据实验结果，我们可以发现，在地球仪的赤道附近，角度变形较小；而在两极附近，角度变形较大。

地图投影的判别与选择第五节地图投影的判别与选择⼀、地图投影的判别地图投影是地图的数学基础，它直接影响地图的使⽤。

地图是地理⼯作者不可缺少的⼯具，有很多地理知识是从图上获得的。

如果在使⽤地图时，不了解投影的特性，往往会得出错误的结论。

例如在⼩⽐例尺等⾓或等积投影图上量算距离，在等⾓投影图上对⽐不同地区的⾯积，以及在等积投影图上观察各地区的形状特征等。

⽬前，国内外出版的地图上⼤多数都注明地图投影名称，这对于使⽤地图，当然是很⽅便的。

但是，也有⼀些地图不注明投影名称和有关说明，因此，我们必须运⽤地图投影的知识，根据不同投影的特征——经纬线形状，结合制图区域所在的地理位置、轮廓形状及地图的内容和⽤途等，综合进⾏分析、判断和进⾏必要的量算来判别它们。

地图投影的判别，主要是对⼩⽐例尺地图⽽⾔。

⼤⽐例尺地图往往是属于国家地形图系列，投影资料⼀般易于查知。

另外由于⼤⽐例尺地图包括的地区范围⼩，不管采⽤什么投影，变形都是很⼩的，在使⽤时可以忽略不计。

判别地图投影⼀般是先根据经纬线⽹形状确定投影种类，如⽅位、圆柱、圆锥等，其次是判定投影的变形性质，如等⾓、等积或任意投影。

（⼀）确定投影种类对于常见的地图投影，⼀般还是⽐较容易确定它的种类的，表2-16列出⼀些常见投影，供判别时参考。

判别经纬线形状的⽅法如下：直线只要⽤直尺量度，便可确定。

判断曲线是否为圆弧，可以将透明纸覆盖在曲线之上，在透明纸上沿曲线按⼀定间隔定出三个以上的点，然后沿曲线移动透明纸，使这些点位于曲线的不同位置，如这些点处处都与曲线吻合，则证明曲线是圆弧，否则就是其他曲线。

判别同⼼圆弧与同轴圆弧，则可以量测相邻圆弧间的垂线距离，若处处相等则为同⼼圆弧，否则是同轴圆弧。

（⼆）确定投影的变形性质当已确定投影的种类后，对有些投影的变形性质是⽐较容易判定的。

例如已确定为圆锥投影，那么只须量任⼀条经线上纬线间隔从投影中⼼向南、北⽅向的变化就可以判别变形性质：如果相等，则为等距投影；逐渐扩⼤，为等⾓投影；逐渐缩⼩，为等积投影。

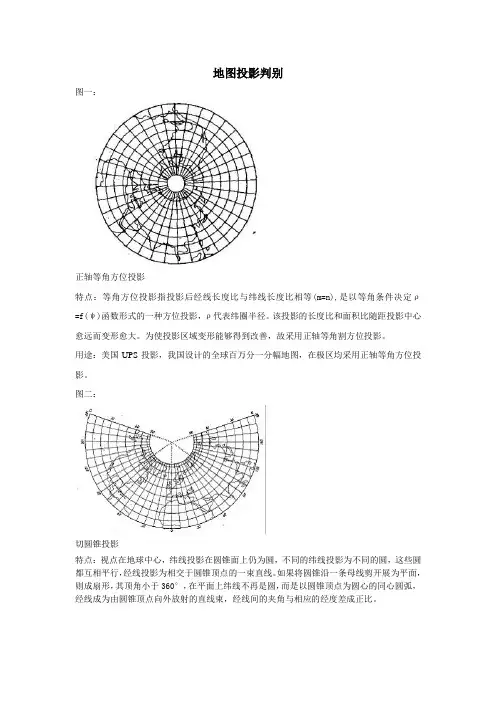
地图投影判别图一：正轴等角方位投影特点：等角方位投影指投影后经线长度比与纬线长度比相等(m=n),是以等角条件决定ρ=f(ψ)函数形式的一种方位投影，ρ代表纬圈半径。

该投影的长度比和面积比随距投影中心愈远而变形愈大。

为使投影区域变形能够得到改善，故采用正轴等角割方位投影。

用途：美国UPS投影，我国设计的全球百万分一分幅地图，在极区均采用正轴等角方位投影。

图二：切圆锥投影特点：视点在地球中心，纬线投影在圆锥面上仍为圆，不同的纬线投影为不同的圆，这些圆都互相平行，经线投影为相交于圆锥顶点的一束直线。

如果将圆锥沿一条母线剪开展为平面，则成扇形，其顶角小于360°，在平面上纬线不再是圆，而是以圆锥顶点为圆心的同心圆弧，经线成为由圆锥顶点向外放射的直线束，经线间的夹角与相应的经度差成正比。

用途：由于圆锥投影具有上述的变形分布规律，因此该投影适于编制处于中纬地区沿纬线方向东西延伸地域的地图，同时，圆锥投影的经纬网又比较简单，所以在中纬度的国家广泛应用。

图三：等距圆锥投影特点：等距圆锥投影上虽然具有长度、面积和角度变形，但变形值却比较小，它的角度变形小于等积圆锥投影，面积变形小于等角圆锥投影。

用途：例如苏联出版的苏联全图。

说明：图二与图三都属于圆锥投影。

圆锥投影的各种变形都是纬度ψ的函数，随纬度变化而变化，而与经度λ无关。

圆锥面与球面相切的切线，或圆锥表面与球面相割的两条割线，即标准纬线。

距标准纬线愈远，其变形愈大。

标准纬线外的变形分布规律均为正变形，而标准纬线之间呈负变形。

图四：正轴等积切圆柱投影特点：正轴等面积切圆柱投影又称“兰勃特等积圆柱投影”。

设将圆柱投影面与球面上赤道相切，按等面积条件，用数学方法将经纬线网投影到圆柱面上。

经线为等距平行直线，纬线为垂直经线的平行直线，纬线间隔随纬度增加而缩小。

角度与长度变形在高纬度地带很显著。

用途：适用于赤道附近地区的地图。

图五：等角圆柱墨卡托投影特点：在等角圆柱投影中，球面上微分圆投影后的图形保持圆形，即一点上的长度比向任何方向均相等。

《地图学》实验指导书1．墨卡托投影图上等角航线与大圆航线绘制1.1目的要求：掌握正轴圆柱投影经纬网建立的方法，并通过在该投影图上绘制等角航线与大圆航线，加深对墨卡托投影性质的理解1.2实习步骤提要：（1）计算赤道周长：（2）计算各条经纬线的平面直角坐标：（3）在墨卡托投影上根据需要规定本初子午线位置，转绘世界大陆轮廓线（1）绘制等角航线（2）在图纸上绘制区域范围为︒︒90~30N N ϕϕ，︒︒90~90W E λλ；中央经线λ0＝180o ，︒=∆10ϕ、︒=∆10λ的正轴球心方位投影经纬网，绘内外图廓1.3仪器用品：直尺、分规、绘图工具、图纸、铅笔、《世界地图》；计算机、制图软件2.地图投影的判别2.1目的要求1、巩固学过的地图投影知识2、掌握识别地图投影系统和分析地图投影变形性质的方法3、为正确使用地图投影奠定基础2.2实习步骤提要（1）利用在说明中介绍的方法，观察地图经纬线形状特征，判别地图的投影系统（2）观察制图区域位置、大小、形状，分析判别地图投影时投影面是与球面相切或相割关系。

（3）量测中央经线上的纬线间间隔变化规律，确定投影的变形性质（4）仍然无法判别其地图投影的变形性质时，则应采取量测计算图上经纬线交点的m ，n ，ε的方法，求算各经纬线交点上的面积比（P ）和最大角度变形（ω）2.3仪器用品：两脚规、三角板、铅笔3.地形图分幅编号3.1目的要求：1、通过具体图幅编号的计算，掌握基本比例尺地形图的分幅和编号的方法2、已知某地的地理坐标为)('46112),('5627E N ︒=︒=λϕ。

用图解法和解析法分别推算出该点所在的1：50万、1：5万、1：1万地形图的分幅和编号3.2实习步骤提要：（1）根据地理坐标，求其所在的1：100万比例尺地形图的图号（2）以经差'30=∆λ，纬差'20=∆ϕ，将1：100万图幅划分为纵向12列，横向12行，即144幅1：10万的图幅，再以该地的经纬度确定1：10万图幅的序号（3）以经差'15=∆λ，纬差'10=∆ϕ，将该地所在的1：10万图幅分成纵向2列，横向2行，共4幅1：5万的图幅，再以该地的经纬度确定1：5万图幅的序号（4）以经差''45'3=∆λ，纬差''30'2=∆ϕ将该地所在的1：10万图幅划分成纵向8列，横向8行，计64幅1：1万的图幅，再以该地的经纬度确定1：1万图幅的序号解析法是建立在图解基础上的另一种推算地形图分幅编号的方法。