底部剪力法应用的原理

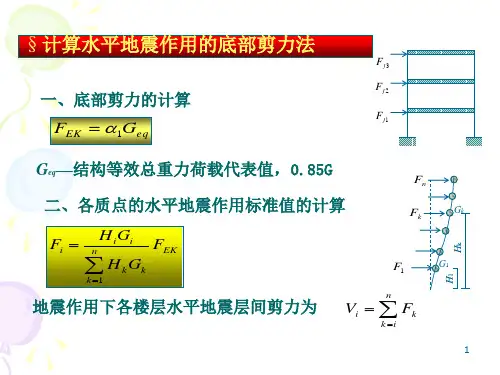
简述确定结构地震作用的底部剪力法的基本原理适用范围和步骤1. 引言1.1 概述底部剪力法是一种常用的结构抗震设计方法，通过对结构底部的剪力进行控制和分配，以提高结构的整体抗震性能。

它基于结构地震作用的特点和结构体系的响应机制，能够较为准确地评估结构在地震作用下的抗震性能，并为工程实践中的建筑设计提供依据。

1.2 文章结构本文将详细介绍底部剪力法的基本原理、适用范围和步骤。

首先，我们将阐述底部剪力概念以及影响结构地震作用的因素；其次，我们将介绍底部剪力法的基本原理及其推导过程；接着，我们将讨论底部剪力法适用范围，并讨论建筑类型、结构形式和地震烈度等因素对其限制；最后，我们将给出底部剪力法的具体步骤，包括确定设计地震加速度谱和周期参数、计算结构质量和弹性刚度分布情况以及确定结构基底剪力分配系数并进行抗震验算。

最后，我们将对底部剪力法的基本原理和适用范围进行总结，并展望其在工程实践中的应用前景。

1.3 目的本文旨在清晰地介绍底部剪力法的基本原理、适用范围和步骤，以帮助读者更好地理解和运用该方法进行结构抗震设计。

通过阐述其基本原理和推导过程，读者可以深入了解底部剪力法的内涵；而讨论其适用范围和局限性则有助于读者准确地选择适合的场景应用该方法；最后，给出的具体步骤可以指导读者在实际工程项目中应用底部剪力法进行抗震设计。

通过本文的阐述，我们希望提高读者对底部剪力法及其应用的认识水平，并促进该方法在工程实践中的广泛应用。

2. 底部剪力法的基本原理2.1 底部剪力的概念底部剪力是指地震作用下，建筑结构底部承受的水平力。

在结构设计中，底部剪力是一个重要的参数，它能够直接体现结构在地震作用下的抗震性能。

2.2 结构地震作用的影响因素对于一个建筑结构来说，其受到地震作用的程度取决于多个因素。

其中包括建筑物所处的地区地震烈度、土壤条件、结构和材料等因素。

这些因素会直接影响到结构所承受的地震力大小及其分布情况。

2.3 底部剪力法的基本原理及其推导过程底部剪力法是一种常用的简化方法，用于确定结构在地震作用下底部所承受的最大水平力。

底部剪力法与振型分解反应谱法的比较分析在研究了多、高层规则的钢筋混凝土-框架结构的水平地震作用中，通过刚度、高度、层数、层高、平面尺寸的变化对底部剪力法与振型分解反应谱法之间的比较分析。

标签：底部剪力法；振型分解反应谱法；等效系数引言底部剪力法[1]适用于基本振型主导的规则和高宽比很小的结构，此时结构的高阶振型对于结构剪力的影响有限，而对于倾覆弯矩则几乎没有什么影响，因此采用简化的方式也可满足工程设计精度的要求。

底部剪力法尚有一个重要的意义就是我们可以用它的理念，简化的估算建筑结构的地震响应，从而在静力的概念上把握结构的抗震能力。

但是在底部剪力法的计算条件上，研究的还不够具体。

通过以振型分解法的计算结果为依据来比较分析底部剪力法的计算条件。

1 工程概况钢筋混凝土-框架结构，层高适中,梁板柱均为现浇柱网布置，混凝土强度C30，结构规则[2-3]，设计地震分组为第一组[4]，设防烈度7度取0.15g，多遇地震，场地类别为1类，周期折减系数取0.6，结构阻尼比为0.05，活载折减系数0.5,等效系数[5]取0.852 刚度影响在刚度的不同分布情况中，除顶层地震剪力偏差较大外，其余各层地震剪力偏差相对较小，总地震剪力偏差在工程计算中还是可以使用的。

以上数据表明：以剪切变形为主（一般轴压比大于0.5），在刚度随高度递减时，其层间位移偏差较小些，一般偏差在20%-30%之间；在刚度随高度分布比较均匀时，层间位移偏差相对要大很多。

3 层数影响采用以剪切变形为主，刚度随高度递减（或均匀型）分布。

通过5、7、10、12、15、20、25、30层来讨论。

底部剪力法计算的顶层地震剪力往往比振型分解法的大，底部剪力法计算的各层地震作用主体是呈倒三角形状，但顶层地震作用明显增大，并且随着层数的增加，顶层地震作用偏差逐渐增大的趋势。

（其主要原因是底部剪力法的理论基础是地震作用竖向呈倒考虑顶部附加地震作用，然而在自振周期过大时（一般为0.75s），此时结果偏大，即附加地震作用偏大，）。

振型分解反应谱法可以考虑多阶振型互相耦合的作用，尤其是扭转振型的耦联，如果只是单阶振型，则振型分解反应谱法和底部剪力法应该是一致的。

所以底部剪力法一般用在低层的、简单的、规则的、对称的结构中，如砌体结构住宅楼或者多层框架（新规范要求加上楼梯就又麻烦了）之类。

此外，振型分解反应谱法计算出来的地震剪力都是绝对值，没有方向，在这一点上，底部剪力法算出不同方向地震作用所引起的剪力的方向，比较有物理意义。

振型分解反应谱法：也称规范法，适用于大量的工程计算，该法有侧刚及总刚两种计算方法，分别对应侧刚模型及总刚模型，其主要区别是侧刚模型采用刚性楼板假定的简化刚度矩阵模型。

总刚模型是采用弹性楼板假定的真实结构模型转化成的刚度矩阵模型。

振型分解反应谱法先计算结构的自振振型，选取若干个振型分别计算各个振型的水平地震作用，将各振型水平地震作用于结构上，求其结构内力，最后将各振型的内力进行组合，得到地震作用下的结构内力和变形。

其基本原理就是用“规范”反应谱，先求得各振型的对应的“最大”地震力，组合后得到结构的组合地震作用。

这里面有一个求“广义特征值”而得出结构前几阶振型和频率的重要步骤，在这个过程中程序按力学和数学的法则进行繁多的中间计算，而不输出中间资料，仅将结果值告知设计人。

底部剪力法：底部剪力法（拟静力法）(Equivalent Base Shear Method) 根据地震反应谱理论，以工程结构底部的总地震剪力与等效单质点的水平地震作用相等，来确定结构总地震作用的方法。

一种用静力学方法近似解决动力学问题的简易方法，它发展较早，迄今仍然被广泛使用。

其基本思想是在静力计算的基础上，将地震作用简化为一个惯性力系附加在研究对象上，其核心是设计地震加速度的确定问题。

该方法能在有限程度上反映荷载的动力特性，但不能反映各种材料自身的动力特性以及结构物之间的动力响应，更不能反映结构物之间的动力耦合关系。

但是，拟静力法的优点也很突出，它物理概念清晰，与全面考虑结构物动力相互作用的分析方法相比，计算方法较为简单，计算工作量很小、参数易于确定，并积累了丰富的使用经验，易于设计工程师所接受。

底部剪力法公式
底部剪力法（Bottom-Up Shear Method）是一种常用于计算混凝土结构中梁的剪力的方法。

该方法的公式如下：
V = ΣVc - ΣVs - Vp
其中，V表示梁的剪力，ΣVc表示混凝土的剪力，ΣVs表示钢筋的剪力，Vp表示预应力筋的剪力。

具体来说，ΣVc的计算方法为：ΣVc = αc ×b ×d ×fck，其中αc为混凝土的剪力系数，一般取0.5；b为梁的宽度；d为梁的有效高度，即截面高度减去钢筋直径的一半；fck为混凝土的强度等级。

ΣVs的计算方法为：ΣVs = ΣAs ×fy / cotθ，其中ΣAs为梁中钢筋的总面积；fy为钢筋的屈服强度；θ为钢筋与水平方向的夹角，一般为45度。

Vp的计算方法因结构形式不同而异。

对于单向受弯梁，Vp可以通过计算预应力筋的拉力得到；对于双向受弯梁，则需要考虑预应力筋的压力和弯矩的作用。

需要注意的是，底部剪力法仅适用于剪力作用在梁底部的情况。

对于剪力作用在梁顶部的情况，应使用顶部剪力法。

此外，还应根据具体结构的特点，选择适当
的计算方法和参数。

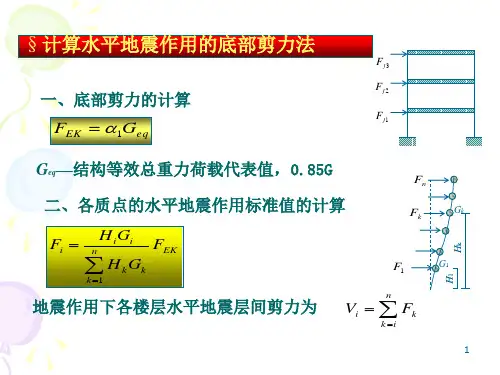
底部剪⼒法--反应谱法--时程分析法概念及分析底部剪⼒法/反应谱法/时程分析法⼀些有⽤的概念从传统的观点来看，底部剪⼒法，反应谱法和时程分析法是三⼤最常⽤的结构地震响应分析⽅法。

那么正确的认识它们的⼀些关键概念，对于建筑结构的抗震设计具有⾮常重要的意义。

HiStruct在此简单的总结⼀些，全当抛砖引⽟。

1. 底部剪⼒法⾼规规定：⾼度不超过40m、以剪切变形为主且质量和刚度沿⾼度分布⽐较均匀的⾼层建筑结构，可采⽤底部剪⼒法。

底部剪⼒法适⽤于基本振型主导的规则和⾼宽⽐很⼩的结构，此时结构的⾼阶振型对于结构剪⼒的影响有限，⽽对于倾覆弯矩则⼏乎没有什么影响，因此采⽤简化的⽅式也可满⾜⼯程设计精度的要求。

底部剪⼒法尚有⼀个重要的意义就是我们可以⽤它的理念，简化的估算建筑结构的地震响应，从⽽⾄少在静⼒的概念上把握结构的抗震能⼒，它还是很有⽤的。

2. 反应谱⽅法⾼规规定：⾼层建筑结构宜采⽤振型分解反应谱法。

对质量和刚度不对称、不均匀的结构以及⾼度超过100m的⾼层建筑结构应采⽤考虑扭转耦联振动影响的振型分解反应谱法。

反应谱的振型分解组合法常⽤的有两种：SRSS和CQC。

虽然说反应谱法是将并⾮同⼀时刻发⽣的地震峰值响应做组合，仅作为⼀个随机振动理论意义上的精确，但是从实际上它对于结构峰值响应的捕捉效果还是很不错的。

⼀般⽽⾔，对于那些对结构反应起重要作⽤的振型所对应频率稀疏的结构，并且地震此时长，阻尼不太⼩（⼯程上⼀般都可以满⾜）时，SRSS 是精确的，频率稀疏表⾯上的反应就是结构的振型周期拉的⽐较开；⽽对于那些结构反应起重要作⽤的振型所对应的频率密集的结果(⾼振型的影响较⼤，或者考虑扭转振型的条件下)，CQC是精确的。

这是因为对于建筑⼯程上常⽤的阻尼⽽⾔，振型相关系数（见⾼规3.3.11-6）在很窄的范围内才有显著的数值。

3.反应谱分析的精确性对于采⽤平均意义上的光滑反应谱进⾏分析⽽⾔，其峰值估计与相应的时程分析的平均值相⽐误差很⼩，⼀般只有百分之⼏，因此可以很好的满⾜⼯程精度的要求，正是在这个平均（普遍性）意义上，我们认为反应谱分析⽅法是精确的。