成都七中2009年外地生招生考试数学模拟试题

四川省成都七中高2009级阶段测试题数学 (理科)班次_____姓名____________学号_____一．选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．设全集U ={1，3，5，7}，集合M ={1，a －5}，,U M U C M ⊆={5，7}，则a 的值为（ ） A. 2 B. 8 C. －2 D. －82. 1 + tan 1501－tan 150 =( )A ．－ 3B ． －3 3C ．3 3D ． 33.已知p ：342x ->，q ：2102x x >--，则﹁p 是﹁q 的（ ）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分又不必要条件4．在等差数列{}n a 中，已知,23=a 则前5项之和等于（ ） A. 10 B. 16 C. 20 D. 525.αβ，是两个不重合的平面，a 、b 是两条不同直线，在下列条件下，可判定α∥β的是( )A. αβ，都平行于直线a 、bB. α内有三个不共线点到β的距离相等C.a 、b 是α内两条直线，且a ∥β，b ∥βD.a 、b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β6．设平面上有四个互异的点A ，B ，C ，D ，已知(2-+)²(-)=0，则 △ABC 的形状一定是 ( )Ａ．直角三角形 Ｂ．等腰三角形 Ｃ．锐角三角形 Ｄ．正三角形7.函数()2x xe ef x --=(x ∈ R )的反函数是1()f x -，则1(2)f - 的值为( )A ．ln(2B ．1ln(22C ．1ln(22+ D ．ln(28．已知]2,2[)(62)(23-+-=，在为常数m m x x x f 上有最大值3，那么此函数在[－2，2]上的最小值为（ ） A ．－37B ．－29C ．－5D ．－119.若()m x x f ++=)cos(2ϕω，对任意实数t 都有)()4(t f t f -=+π，且1)8(-=πf ，则实数m 的值等于( )A.±1B.±3C.－3或1D.－1或3 10.如图，正五边形ABCDE 中，若把顶点A 、B 、C 、D 、E 染上 红、黄、绿、三种颜色中的一种，使得相邻顶点所染颜色不相同，则不同的染色方法共有 （ ） A ．30种 B ．27种 C ．24种 D ．21种ECBA DED CB A11. 如图，在矩形ABCD 中，4,3,AB BC E ==是CD 的 中点，沿AE 将ADE ∆折起，使二面角D AE B --为60︒，则四棱锥D ABCE -的体积是（ ）.939 2739 913 271312. 已知函数),2[)(+∞-的定义域为x f ，且)2()4(-=f f ，)()(x f x f 为')(x f y '=的图象如图所示.则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00y x f y x 所围成的面积是( )A ．2B ．4C ．5D ．8二．填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上） 13．当6)1(x x x -的展开式的第5项的值等于215，x = ，此时=+++∞→)111(lim 2n n xx x .14．已知yx y x R y x 1114*,+=+∈，则，且的最小值为_______. 15.已知过球面上A 、B 、C 三点的截面和球心的距离是球半径是14，且5,0AB AC BC =⋅= ，那么球的表面积为_______________.16．关于函数21()lg (0),x f x x x+=≠有下列命题：①其图像关于y 轴对称；②当x ＞0时，()f x 是增函数；当x ＜0时，()f x 是减函数；③()f x 的最小值是lg 2；④当10,2x x -<<>时，()f x 是增函数；⑤()f x 无最大值，也无最小值.其中所有正确结论的序号是 .高2009级数学阶段测试题(理科)班次_____姓名____________学号_____1314 15 1617．（本小题满分12分）已知5||5||8011AC AB AD DB CD AD ===⋅= ，，，，(1)求||AB AC - ；(2)设BAC θ∠=，且已知4cos()54πθx πx +=-<<-，，求sin x . 18．（本小题满分12分） 如图，直四棱柱ABCD —A 1B 1C 1D 1的高为3，底面是边长为4且∠DAB=60°的菱形，AC ∩BD=0，A 1C 1∩B 1D 1=O 1，E 是O 1A 的中点. （1）求二面角O 1－BC －D 的大小； （2）求点E 到平面O 1BC 的距离.19．（本小题满分12分）已知{a n }为等比数列，{b n }为等差数列，其中a 2=b 4,a 3=b 2,a 4=b 1，且a 1=64,公比q ≠1（Ⅰ）求a n ,b n ；（Ⅱ）设c n =log 2a n ，求数列{c n a n }的前n 项和T n 20. （本小题满分12分）已知函数f （x ）的图象与函数h （x ）=x +x1+2的图象关于点A （0，1）对称. （1）求f （x ）的解析式； （2）若g （x ）=f （x ）+xa,且g （x ）在区间（0，2］上为减函数，求实数a 的取值范围. 21.（本小题满分13分）已知函数241)x (f x +=)R x (∈.(1) 求()(1)f x f x +-的值(2) 若数列}a {n 的通项公式为)m ,,2,1n ,N m ()mn(f a n =∈=+, 求数列}a {n 的前m 项和;S m(3) 设数列}b {n 满足: 31b 1=, n 2n 1n b b b +=+. 设1b 11b 11b 1T n 21n ++++++= . 若(2)中的n S 满足对任意不小于2的正整数n, n n T S <恒成立, 试求m 的最大值.22．(本小题满分13分) 已知函数21f(x)=lnx,g(x)=ax +bx (a 0).2≠（I ）若a= 2 , h(x)=f(x)g(x)－时函数－ 在其定义域是增函数，求b 的取值范围；（II ）在（I ）的结论下，设函数2x x (x)=e +be ,x ∈[0,ln2],求函数(x)ϕϕ的最小值；（III ）设函数)(x f 的图象C 1与函数)(x g 的图象C 2交于点P 、Q ，过线段PQ 的中点R 作x 轴的垂线分别交C 1、C 2于点M 、N ，问是否存在点R ，使C 1在M 处的切线与C 2在N 处的切线平行？若存在，求出R 的横坐标；若不存在，请说明理由. 参考解答：1.B.因为U ={1，3，5，7}，,U M U C M ⊆={5，7}，{}1,3,53,8M a a ∴=∴-==2.D.00000001tan15tan 45tan15tan 601tan151tan 45tan15++===-- 3.A.2:2;:12,3p x q x p q ⌝≤≤⌝-≤≤∴⌝⊂⌝4.A.5123453510S a a a a a a =++++== .5.D. A 错，若a ∥b ，则不能断定α∥β；B 错，若A 、B 、C 三点不在β的同一侧，则不能断定α∥β；C错，若a ∥b ，则不能断定α∥β；D 正确.226..2()()()()0,B DB DC DA DB DA DB DA AB AC AB AC AB AC AB AC AB AC+-=-+-=+∴+-=-=∴=7.D.22ln(22x xx e e e x --=⇒== 由. 8．A 解析：，可得，令2,00)(126)(212==='-='x x x f x x x f 故在[－2，2]上最大值为3)0(==m f ，所以最小值为37)2(-=-f .()(),48()12,()12,1-388f t f t x f m f m m ππππ+=-==-=-+=-=+∴= 9.由可知图象的一条对称轴为或，应选C.10..10310=30A A ⨯列举法：点染红色有种方法，所以共有种方法011.A.,,60,9,.13ABCE D ABCE D DO ABCE DF AE F DOF DFO DF S V A -⊥⊥∠∆∠=∴=== 过点作面作于连结FO,则DFO 为平面角，易求在中，又应选[])()-2002x y 0y f x =+∞+≥ 12.B.由图像可知在，减函数是，在，上是增函数，又 B.4,,4200,42),4(1)2(应选面积为可行域为直角三角形其画出可行域，⎪⎩⎪⎨⎧≤+≥≥∴≤+∴=≤+∴y x y x y x f y x f 二．填空题42456111513.(()15,22T C x x x =-=⨯=∴= 22111111111(1)122222lim n n n nn x x x →+∞+++=+++=--= ， 14. 9.∵9454411*,,≥++=+++=+∴∈yxx y y y x x y x y x R y x 当且仅当61,31==y x 取等号 112222115.,,0,45152080,()()24233O O R AC BC AB R R R S π=⋅=∴∴-=⇒=⇒=设球心为O 截面圆O ，则为截面圆的直径r=由min min 116.()lg(),()(),(1)01,(),1,()212,()lg 2,(3)(1,0),(2,),1()()4)(3)(5).134f x x f x f x xx f x x f x x f x xg x x f x x=+∴-=∴<<≥∴+=∴=∴-+∞=+∴∴∴ 正确；当时为减函数时为增函数，（）不正确；（）正确；在上单增，为增函数，（正确；正确,不正确因此正确的为（）（）（）三．解答题：17.解：(1)由已知，5|||016AD AB CD AD =⋅=5|=，且，2即CD AD ⊥， 所以1cos 2BAC ∠== ，… 3 分由余弦定理||||7AB AC BC -=== ；… 6 分(2)由(1)，14cos cos()cos()2335ππθθθx x ==+=+=，，，所以3sin()35πx +=±，243312πππππx x -<<--<+<而，，… 8 分如果0312ππx <+<，则13sin()sin sin 312625πππx +<<=<，所以3sin()35πx +=-，… 10 分此时3sin sin[()]3310ππx x +=+-==- .… 12 分18．解法一（1）过O 作O F ⊥BC 于F ，连接O 1F ，∵OO 1⊥面AC ，∴BC ⊥O 1F ，… 2分 ∴∠O 1F O 是二面角O 1－BC －D 的平面角，∵OB=2，∠OB F =60°，∴O F… 4分 在Rt △O 1O F 在，tan ∠O 1FO=1OO OF ==∴∠O 1F O=60° 即二面角O 1—BC —D 为60°… 6分（2）在△O 1AC 中，OE 是△O 1AC 的中位线，∴OE ∥O 1C ，∴OE ∥O 1BC ，… 2分∵BC ⊥面O 1OF ，∴面O 1BC ⊥面O 1O F ，交线O 1F .过O 作OH ⊥O 1F 于H ，则OH 是点O 到面O 1BC 的距离，∴OH=3.2∴点E 到面O 1BC 的距离等于3.2… 6分解法二：（1）∵OO 1⊥平面AC ， ∴OO 1⊥OA ，OO 1⊥OB ，又OA ⊥OB ， 建立如图所示的空间直角坐标系（如图） ∵底面ABCD 是边长为4，∠DAB=60°的菱形， ∴OB=2，则A （23，0，0），B （0，2，0），C （－0，0），O 1（0，0，3）… 2分设平面O 1BC 的法向量为1n=（x ，y ，z ）， 则1n ⊥1O B ，1n ⊥1OC，∴23030y z z -=⎧⎪⎨--=⎪⎩，则z=2，则x =y=3， ∴1n =3，2），而平面AC 的法向量2n =（0，0，3）… 4分 ∴cos<1n ，2n21436||||2121=⨯=⋅n n ， 设O 1－BC －D 的平面角为α， ∴cos α=1,2∴α=60°.故二面角O 1－BC －D 为60°.… 6分 （2）设点E 到平面O 1BC 的距离为d ，… 1分∵E 是O 1A 的中点，∴1EO =0，32），… 3分则d=2323)3(|)2,3,3()23,0,3(|||||22211=++--⋅-=⋅n n EO ∴点E 到面O 1BC 的距离等于32.… 6分 19.解：（I ）依题意032),(32244342=+--+=a a a a a a a 即 03213131=+-∴q a q a q a …2分，21101322==⇒=+-∴q q q q 或211=∴≠q q …4分1)21(64-⨯=n n a 故 ，bn=8+8³(n-1)=8n 5分 （II ）n c nn n -==⨯=--72log ])21(64[log 7212 …………6分()()()()()()()⎪⎪⎭⎫ ⎝⎛⨯--⎪⎭⎫ ⎝⎛+++-=-----⎪⎭⎫ ⎝⎛⨯-+⨯+⨯+⨯=----⎪⎭⎫ ⎝⎛⨯-++⨯+⨯+⨯=-----1n 2n 0n2101121021n 72121211264T 122217214215216642121721421521664 得n n n n n T n T()7215-n 640-⎪⎭⎫⎝⎛+=∴n n T …………12分20.解:（1）设f （x ）图象上任一点坐标为（x ,y ），点（x ,y ）关于点A （0，1）的对称点（－x ,2－y ）在h （x ）图象上.∴2－y =－x +x -1+2.∴y =x +x 1, 即f （x ）=x +x1.… 4分 （2）g （x ）=x + xa 1+,∵g ′（x ）=1－21x a +,… 8分，g （x ）在（0，2］上递减，∴1－21xa +≤0在x ∈（0,2］时恒成立,，a ≥x 2－1在x ∈（0,2）时恒成立.… 10分∵x ∈（0,2]时，（x 2－1） max =3,∴a ≥3.… 12分 21．（本小题满分13分）解: 001111411()(1)4242422(42)2x x x x x f x f x -+-=+=+=++++ （）…4分 (2)由(1)可知, 21)x 1(f )x (f =-+, 所以)1m k 1(21)m k 1(f )m k (f -≤≤=-+ ,即,21a a , 21)m k m (f )m k (f k m k =+∴=-+- ………………6分 由m 1m 321m a a a a a S +++++=- , ……………… ① 得,a a a a a S m 13m 2m 1m m +++++=--- ………………②由①＋②, 得,612m 61221m a 221)1m (S 2m m -=⨯+-=+⨯-= ∴).1m 3(121S m -=……8分 (3) ∵,31b 1=)1b (b b b b n n n 2n 1n +=+=+,……③，对任意的0b ,N n n >∈+ .……④由③、④, 得,1b 1b 1)1b (b 1b 1n n n n 1n +-=+=+即1n n n b 1b 11b 1+-=+. ∴1n 1n 11n n 3221n b 13b 1b 1)b 1b 1()b 1b 1()b 1b 1(T +++-=-=-++-+-= . ∵,b b ,0b b b n 1n 2n n 1n >∴>=-++ ∴数列}b {n 是单调递增数列. ∴n T 关于n 递增. 当2n ≥, 且+∈N n 时, 2n T T ≥.……10分∵,8152)194(94b ,94)131(31b ,31b 321=+==+==∴.5275b 13T T 12n =-=≥…12分 ∴,5275S m <即,5275)1m 3(121<-∴,394639238m =< ∴m 的最大值为6. ………13分 22．解：（I ）依题意：.ln )(2bx x x x h -+=()h x 在（0,+∞）上是增函数，1()20h x x b x'∴=+-≥对x ∈（0,+∞）恒成立， …………2分∴≤+>+≥ 112.0,则2b x x x x x(].22,∞-∴的取值范围为b …………4分（II ）设].2,1[,,2∈+==t bt t y e t x则函数化为22().1,2[1,2],242b b by t b y =+-∴-≤-≤≤ 当即在上为增函数当t=1时，y m I n =b+1；…………6分,]2,1[4,22;42,24,2212min 上是减函数在函数时即当时当时即当y ，b bb ，y b t b b -≤≥--=-=-<<-<-< 当t=2时，y m I n =4+2b…………8分.4)(,24.1)(,222,2b x b b x b --<<-+≤≤-的最小值为时当的最小值为时当综上所述ϕϕ当)(,4x b ϕ时-≤的最小值为.24b +…………9分（III ）设点P 、Q 的坐标是.0),,(),,(212211x x y x y x <<且则点M 、N 的横坐标为.221x x x +=C 1在点M 处的切线斜率为.2|1212121x x x k x x x +==+=C 2在点N 处的切线斜率为.2)(|212221b x x a b ax k x x x ++=+=+=…………10分假设C 1在点M 处的切线与C 2在点N 处的切线平行，则.21k k =22122121211212222221121211()2()()2.()22()()ln ln ln ,22a x x x x a x x b b x x x x x x x a a x bx x bx y y x x x +--=+=+-++=+-+=-=-=即则……………11分.1)1(2)(2ln 1212211212x x x x x x x x x x +-=+-=∴设,1,1)1(2ln ,112>+-=>=u uu u x x u 则 ……………… ①[)2222(1)14(1)()ln , 1.().1(1)(1)1,()0.()1,,2(1)()(1)0,ln .1u u r u u u r u u u u u u u r u r u u r u r u u --'=->=-=+++'>∴>+∞->=>+ 令则所以在上单调递增故则这与①矛盾，假设不成立.故C 1在点M 处的切线与C 2在点N 处的切线不平行.…13分。

成都七中2009级高三年级二诊模拟考试理科综合试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷第1至6页，第Ⅱ卷7至16页。

共300分，考试时间150分钟。

第Ⅰ卷(选择题共126分)注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、学号、考试科目涂写在答题卡上。

考试结束，将答题卡交回。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上。

可能用到的原子量：H-1 O-16 S-32 Na-23 C-12 N-14 Fe-56一、本大题共13题，每题6分，共78分。

在下列各题的四个选项中，只有一个选项是符合题目要求的。

1．为了研究酵母菌胞内蛋白质的合成，研究人员在其培养基中添加3H标记的亮氨酸后，观察相应变化。

不可能出现的结果是A.细胞核内出现3H 标记B.内质网是首先观察到3H 标记的细胞器C.培养一段时间后，细胞膜上能观察到3H标记D.若能在高尔基体上观察到3H标记，表示可能有分泌蛋白合成2．对下列四幅图的描述正确的是A．图1细胞周期中a阶段X射线照射可诱发突变，b阶段用秋水仙素能抑制纺锤体的形成B．图2中的温度在b时酶活性较低是因为底物与酶分子可逆性结合C．图3中bc段和de段的变化都会引起C3含量的下降D．图4中造成cd段下降的原因在有丝分裂和减数分裂中是不同的3．下图是基因突变鼠和正常鼠在进食不运动和进食且运动两种状态下血糖浓度的变化。

根据图中信息，基因突变鼠出现所述状况的原因最可能是A．胰岛B细胞受损 B．B淋巴细胞受损C.无法将血糖转换成肝糖元D．体内细胞缺乏胰高血糖素的受体4．接种牛痘病毒可以预防天花的根本原因是A．牛痘病毒和天花病毒遗传信息相同B．牛痘病毒和天花病毒遗传性状相同C．牛痘病毒和天花病毒携带同一种抗原物质D．接种牛痘病毒引起的免疫是非特异性免疫5．下列关于物种与种群的说法正确的是A．多倍体植物物种的形成不需要经过隔离B．外来物种的入侵是我国生物多样性减少的主要原因C．种群基因库间的差异是产生生殖隔离的根本原因D．种群的S型增长主要受自身种群密度的制约，与种间斗争无关6．“三鹿问题奶粉”事件发生后，引起了国家的高度重现，对婴幼儿奶粉进行了三聚氰胺全国专项监督检查，结果令人震惊。

成都七中2009年外地生招生考试数学模拟试题第1页(共8页成都七中2009年外地生招生考试数学模拟试题(考试时间120分钟,满分150分第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。

2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。

不能答在试卷纸上。

3.考试结束后,监考员将第Ⅰ卷、第Ⅱ卷和答题卡一并收回。

一、单项选择(共12小题,每小题5分,满分60分每小题只有一个选项符合题意。

1.已知二次函数c bx ax y ++=2(0≠a 的图象如图所示, 则下列结论①0<++c b a②0<+-c b a ③02<+a b ④0>abc 其中正确的个数是 A .1个 B .2个C .3个D .4个2.如图,O 是线段BC 的中点,A 、D 、C 到O 点的距离相等。

若30=∠ABC ,则ADC ∠的度数是 A .30°B .60°C .120°D .150°3.如图,△ACB 内接于⊙O ,D 为弧BC 的中点,ED 切⊙O 于D的延长线相交于E ,若AC =2,AB =6,ED +EB =6,那么A .2B .4C .6D .84.现有A 、B 两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6用小丽掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P ,(y x 。

那么它们各掷一次所确定的点E DC成都七中2009年外地生招生考试数学模拟试题第2页(共8页P 落在已知抛物线x x y 42+-=上的概率为 A .118 B .112 C .19 D .165.不等式组4831531x x -≥--<- 的所有整数解的和是A .—1B .0C .1D .26.如果自然数a 是一个完全平方数,那么与a 之差最小且比a 大的一个完全平方数是A .1a +B .21a+ C .221a a ++ D .1a +7.如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a =1,则这个正方形的面积为A B C .2D .(21 8.对于两个数,200820092009M =⨯,200920082008N =⨯。

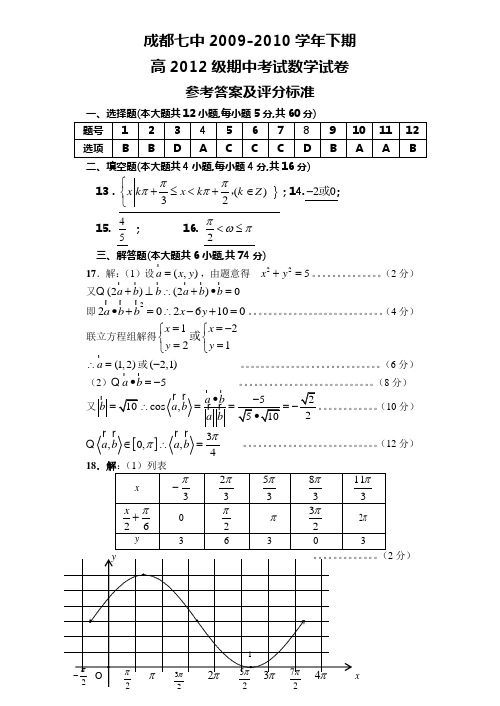
成都七中2009-2010学年下期高2012级期中考试数学试卷参考答案及评分标准一、选择题(本大题共12小题,每小题5分,共60分)二、填空题(本大题共4小题,每小题4分,共16分)13．}()32x k x k k Zππππ⎧+≤<+∈⎨⎩，；14.20-或;15.45；16.2πωπ<≤三、解答题(本大题共6小题,共74分)17．解：（1）设(,)a x y=，由题意得225x y+=。

（2分）又(2)(2)0a b b a b b+⊥∴+∙=即22026100a b b x y∙+=∴-+=。

（4分）联立方程组解得1221x xy y==-⎧⎧⎨⎨==⎩⎩或(1,2)a∴=或(2,1)-。

（6分）（2）5a b∙=-。

（8分）又10b=cos,25a ba ba b∙∴===-∙。

（10分）[]3,0,,4a b a bππ∈∴=。

（12分）2分）。

（4分）(2)周期T ＝π4，振幅A ＝3，初相6πϕ=，由262πππ+=+k x ，得)(322Z k k x ∈+=ππ即为对称轴；。

（8分） （3）①由x y sin =的图象上各点向左平移6πϕ=个长度单位，得)6sin(π+=x y 的图象；②由)6sin(π+=x y 的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得)62sin(π+=x y 的图象；③由)62sin(π+=x y 的图象上各点的纵坐标伸长为原来的3倍（横坐标不变），得)62sin(3π+=x y 的图象；④由)62sin(3π+=x y 的图象上各点向上平移3个长度单位，得)62sin(3π+=x y ＋3的图象。

（12分）19．解：（1）(cos 3,sin ),(cos ,sin 3),AC BC αααα=-=-。

（2分）||(cos AC ∴=||cos BC ==。

（4分） 35||||sin cos .(,),.224AC BC πππαααα==∈∴=得又。

成都七中2008年外地生招生考试数学试题考试时间120分钟 满分150分注：请将选择题的正确选项填涂到季度卡上一、选择题（每小题只有一个正确答案，共10个小题，满分60分）1、已知三个整数a,b,c 的和为奇数，那么abc c b a 2222+-+ （ ）A 、一定是非零偶数B 、等于零C 、一定为奇数D 、可能是奇数，也可能是偶数。

2、已知3 2c b a 1abc 222=++=++=c b a ，，， 则111111-++-++-+b ca a bc c ab 的值是（ ） A 、1 B 、21- C 、2 D 、32-3、设02=+-q px x 的二实根为βα，，而以22βα，为根的二次方程仍是02=+-q px x ，则数对),(q p 的个数是（ ）A 、2B 、3C 、4D 、04、设函数543222-----=k k kx x y 的最大值为M ，为使M 最大，k= ( )A 、-1B 、1C 、-3D 、35、若132=-x x ，则=+--+200872129234x x x x （ ）A 、2011B 、2010C 、2009D 、20086、已知坐标原点O 和点)-2,A(2，B 是坐标轴上的一点，若AOB ∆是等腰三角形，则这样的点B 一共有多少个 （ ）A 、4B 、5C 、6D 、87、如图：有六个面积为1的正方形组成的长方形，其中有A 、B 、C 、D 、E 、F 、G 7个点，以这7个点为顶点，并且面积为1的三角形有 （ ）A 、11个B 、12个C 、13个D 、14个8、锐角ABC ∆的三边两两不等，D 是BC 边上的一点，︒=∠+∠90C BAD ，则AD 一定过ABC ∆的 （ ） A 、垂心 B 、内心 C 、外心 D 、重心9、有纯农药一桶，倒出20L 后用水补满，然后又倒出10L ，再用水补满，这时，桶中纯农药与水的容积之比为3：5，则桶的容积为（ ）A 、30B 、40C 、50D 、60 A B CD EF G10、如图，直线4321//////l l l l ，相邻两条平行线间的距离都等于1，若正方形ABCD 的四个顶点分别在四条直线上，则它的面积等于（ ）A 、4B 、5C 、24D 、25二、填空题（每小题6分，满分48分）11、如图正方形的每一个面上都有一个自然数，已知相对的两个面上二数之和都相等，若13、9、3的对面的书分别为a,b,c,则 =---++bc ac ab c b a 222 12、已知等边ABC ∆外有一点P ，设P 到BC 、CA 、AB 的距离分别为321h ,h ,h ,且63h2-h1=+h ,那么等边ABC ∆的面积为13、Rt ABC ∆中，︒=∠90C ，若sinA 和sinB 是方程022=--k x x 的两个根，则k=14、在ABC ∆中，2AC =,D 是AB 的中点，E 是CD 上一点，CD 31ED =， 若AE CE AB CE ⊥=且31,则BC= 15、方程22323=--+x x 的解为16、在正八边形中，与所有边均不平行的对角线有 条17、若正整数n 恰好有4个正约数，则称n 为奇异数，例如6、8、10都是奇异数，那么在27、42、69、111、125、137、343、899、3599、7999这10个正整数中奇异数有 个18、如图，MN 是半圆O 的半径，A 是半圆的一个三等分点，B 是中点，P 是直径MN 上的点，若PB AP +的最小值为22厘米， 则圆的半径r = 厘米1l 2l 3l 4l A B C D 3913三、解答题（每小题14分，满分42分）19、（1）已知抛物线3)3(2--+=x m mx y )0(>m 与x 轴交于点)0,(1x A ，)0,(2x B )21(x x <与y 轴交于点C 且AB=4,圆M 过A 、B 、C 三点，求扇形MAC 的面积S 。

成都七中高2009级模拟高考数学（理科）试题一.本大题共 12 小题，每小题 5 分，共 60 分. 在每小题列出的四个选项中，选出符合题目要求的一项.{}21.60,,.13.14.15.16A x x x x Z A ABCD =+-<∈设集合则集合的非空真子集的个数是2.()2cos 2....242f x x x A B C D ππππ=-函数的最小正周期是223.4422...x y xy x y A B D +<+>+是成立的充分不必要条件必要不充分条件C.充要条件既不充分也不必要条件020log (2)4.()()11()(2)2.(,0)(2,).(0,2).(,1)(3,).(1,3)x x f x f x x x A B C xD ≥⎧⎪=>⎨<⎪⎩-∞+∞-∞-+∞-U U 设函数若，则的取值范围是[]25.()2,0,32.3.4.5f x x x a x a Aa B a C a D a =-+∈>>>>已知函数的任意三个函数值总可以作为一个三角形的三边长，则的取值范围是cos 26.,(sin cos )2sin()411...2.222A B C D θθθπθ=--+--若则的值为27.,0.1.2.3A B B C D 过抛物线y =4x 的焦点作一条直线与抛物线相交于两点，它们的横坐标之和等于5，则这样的直线的条数是A.{}287118.1829999...99.942n n a n S a a a S A B C D +=-为等差数列，前项和为，若，则的值为9.,220....2222x y x y x Z x y x y A B C D -≥⎧⎪⎪≤=-⎨⎪+≥⎪⎩--实数满足不等式，目标函数的最小值为121210.1.2..l l B C D αβαβo 如图所示，在120的二面角--内圆O 与圆O 分别在半平面,内，且与棱相切于同一点P,则以圆O 和圆O 为截面的球A.仅有个仅有个有无数个不存在2211.14.6.4.10.8ax by x y A B C D +=+=直线与圆的交点为整点（横纵坐标均为整数的点），则这样的直线的条数是[)1312.()(3)(),0,1()31(log 36)107135....33336x f x f x f x x f x f A B C D +=∈=-=----已知奇函数满足当时，则二.填空题：本大题共 4小题，每小题 4 分，共 16 分. 把答案填在题中横线上26113.()x x -的展开式中常数项为________（用数字作答）14.2a b a b αα-r r r r向量=(cos ,sin ),向量则的最大值是_____.15.7甲，乙两人之间进行一场打完局的比赛，且每局无平局，则比赛结果出现甲比乙为4：3的概率是______.16.给出下列命题：①函数(1)y f x =-和(1)y f x =-的图像关于直线1x =对称②00(),()0R f x x R f x '∈>在上连续的函数若是增函数，则对任意均有成立 ③底面是正三角形，侧面是等腰三角形的三棱锥是正三棱锥。

成都七中2009年外地生招生考试 数学模拟试题参考答案及评分标准第Ⅰ卷一、单项选择（共12小题，每小题5分，满分60分）第Ⅱ卷二、填空题 （共4小题，每小题4分，满分16分）13．2 14． 3520 15． 211≤<-m 16．4n+2三、计算题 （共6小题，满分74分）17．（本小题满分12分）（1）解：原式=xy y xy x y xy x 25)23(4422222--+-++=x y y xy x y xy x 25234422222-+--++·······················2分=xxy x 2222+-=y x +-······················································2分当2-=x ，21=y 时原式=2521)2(=+--··························2分 （2）解： 联立21y x =+和2331y x x =+- 可得133122-+=+x x x ········2分化简可得0232=-+x x 解方程，得11-=x 322=x ········································2分 当11-=x 时，11-=y 则一交点为)1,1(-- 当322=x 时，372=x 则一交点为)37,32( 综上所述，直线21y x =+与抛物线2331y x x =+-的交点坐标为)1,1(--，)37,32(·················································2分18．（本小题满分12分） 解： （1）··························4分（2）·································1分·············2分······················································2分 （3）································1分·········································2分222211tan tan 232342AB PC BPC ABE ADEPFE DFP PFE DFPPF DF PF EF FD EF PFAEAB AE BP AE AE APB ABE PE BE AE a PE a BE a AP a AE PE BE PC PC PE PB PC FC FE FD PF PF FC ∴∠=∠=∠∠=∠∴∴=∴=⋅∴⊥∠==∠=======∴====∴=⋅=∴==⋅=∴==∥又△∽△连接为直径令，，为切线12190PCPF ADB AB ADB PE PB PA PDPD BD AD ADBRt =∴=∴∠=︒⋅=⋅∴===∴△为等腰直角三角形为直径△为等腰△19．（本小题满分13分）（1）连结。

--成都七中2009年外地生招生考试数 学 模拟试题（考试时间120分钟，满分150分）第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

不能答在试卷纸上。

3．考试结束后，监考员将第Ⅰ卷、第Ⅱ卷和答题卡一并收回。

一、单项选择（共12小题，每小题5分，满分60分）每小题只有一个选项符合题意。

1．已知二次函数c bx ax y ++=2（0≠a ）的图象如图所示，则下列结论 ①0<++c b a ②0<+-c b a ③02<+a b ④0>abc 其中正确的个数是 A ．1个 B ．2个C ．3个D ．4个2．如图，O 是线段BC 的中点，A 、D 、C 到O 点的距离相等。

若ο30=∠ABC ，则ADC ∠的度数是 A ．30° B ．60° C ．120° D．150°C--3．如图，△ACB 内接于⊙O，D 为弧BC 的中点，ED 切⊙O 于D ，与AB 的延长线相交于E ，若AC ＝2，AB ＝6，ED ＋EB ＝6，那么AD=A ．2B ．4C ．6D ．8 4．现有A 、B 两枚均匀的小立方体（立方体的每个面上分别标 有数字1，2，3，4，5，6）用小丽掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P ),(y x 。

那么它们各掷一次所确定的点P 落在已知抛物线x x y 42+-=上的概率为A ．118 B ．112 C ．19 D ．165．不等式组4831531x x -≥--<- 的所有整数解的和是A ．—1B ．0C ．1D ．26．如果自然数a 是一个完全平方数，那么与a 之差最小且比a 大的一个完全平方数是A ．1a +B ．21a+ C ．221a a ++ D ．21a +7．如图，若将左图正方形剪成四块，恰能拼成右图的矩形，设a =1,则这个正方形的面积为A ．72+B ．32+C ．2D ．(21 8．对于两个数，200820092009M =⨯，200920082008N =⨯。

成都七中高中数学竞赛试题成都七中作为中国知名的中学之一，其高中数学竞赛试题往往具有较高的难度和创新性。

以下是一套模拟的成都七中高中数学竞赛试题，供参考：一、选择题（每题4分，共20分）1. 设集合A={1,2,3}，B={2,3,4}，则集合A∩B的元素个数为：A. 1B. 2C. 3D. 42. 函数f(x)=|x-2|+|x-3|的最小值是：A. 1B. 2C. 3D. 43. 若a, b, c是实数，且满足a^2+b^2+c^2=1，求a+b+c的最大值：A. 1B. 2C. 3D. 44. 已知等差数列的前三项和为S，若S=9，且第二项a_2=5，求首项a_1：A. 2B. 3C. 4D. 55. 对于任意实数x，不等式|x-1|+|x-2|+|x-3|≥k恒成立，求k的最小值：A. 3B. 4C. 5D. 6二、填空题（每题5分，共15分）6. 圆的方程为(x-2)^2+(y-3)^2=1，求圆心到直线x+2y-7=0的距离。

7. 已知数列{an}是等比数列，且a1=2，a3=18，求公比q。

8. 求解一元二次方程x^2-4x+4=0的根。

三、解答题（每题10分，共65分）9. 证明：对于任意正整数n，1^2 + 1/2^2 + 1/3^2 + ... + 1/n^2 < 2。

10. 解不等式：|x-1| + |x-2| + |x-3| ≥ 9。

11. 已知函数f(x)=x^3-3x^2+2x-1，求其导数f'(x)，并求在区间[0,2]上的最大值和最小值。

12. 某工厂生产一种产品，每件产品的成本为c元，销售价格为p元。

已知生产x件产品时，总成本为C(x)=cx，总收入为R(x)=px，利润为L(x)=R(x)-C(x)。

求利润最大化时的产量。

13. 已知椭圆的方程为x^2/a^2 + y^2/b^2 = 1（a>b>0），求椭圆的焦点坐标。

14. 证明：对于任意实数x，e^x > 1 + x。

2009年成都七中嘉祥外国语学校小升初奖学金数学考试题答案一、填空（每题6分共96分）1、计算：1122343625%++1+2.5=35221+1.254⨯⨯÷÷。

2、一天,甲、乙、丙三人去郊外钓鱼已知甲比乙多钓9条,丙钓的是甲的2 倍,比乙多钓22条,问他们三人一共钓了条。

3、一只猴子摘了一堆桃子，第一天它吃了这堆桃子的七分之一；第二天它吃了余下桃子的六分之一；第三天它吃了余下桃子的五分之一；第四天它吃了余下桃子的四分之一；第五天它吃了余下桃子的三分之一；第六天它吃了余下桃子的二分之一。

这时还剩下12只桃子，那么前三天猴子所吃桃子的总数是_______。

4、如图，由正方形和半圆形组成的图形。

其中P点为半圆周的中点，Q为正方形一边的中点。

那么阴影部分面积是_________ 。

（圆周率π=3.14）5、111111111357911131517612203042567290++++++++=6、大于而小于11的分数中，分母为6的最简分数，一共有个。

7、张佳从甲地向乙地走，莉莉同时从乙地向甲地走，当他俩各自达到终点时，又迅速返回。

两人行走过程中，各自速度不变。

两人第一次相遇在距甲地50米处，第二次相遇在距乙地18米处。

甲、乙两地向距米。

8、用甲、乙两种糖配成什锦糖，如果用3份甲种糖和2份乙种糖配成什锦糖，比用2份甲种糖和3份乙种糖配成的什锦糖每千克贵1.32元，那么1千克甲种糖比1千克乙种糖贵元。

9、某学校五年级共有110人，参加语文、数学、英语三科活动小组，每人至少参加一组。

已知参加语文小组的有52人，只参加语文小组的有16人；参加英语小组的有61人，只参加英语小组的有15人；参加数学小组的有63人，只参加数学小组的有21人。

那么三组都参加的有__ 人。

10、如果某整数同时具备如下三条性质：（1）这个数与1的差是质数；（2）这个数除以2所得的商也是质数；（3）这个数除以9的余数是5。