《水力学》第二章答案

第二章:水静力学 一：思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答：水头是压强的几何意义表示方法，它表示h 高的水头具有大小为ρgh 的压强。

绝对压强预想的压强是按不同的起点计算的压强，绝对压强是以0为起点，而相对压强是以当地大气压为基准测定的，所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压，即真空。

某点负压大小等于该点的相对压强。

Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中，z 表示某点在基准面以上的高度，称为位置水头，g p ρ表示在该点接一根测压管，液体沿测压管上升的高度，称为测压管高度或压强水头，g p z ρ+称为测压管水头，即为某点的压强水头高出基准面的高度。

关系是：（测压管水头）=（位置水头）+（压强水头）。

2-5.等压面是压强相等的点连成的面。

等压面是水平面的充要条件是液体处于惯性坐标系，即相对静止或匀速直线运动的状态。

2-6。

图中A-A 是等压面，C-C,B-B 都不是等压面，因为虽然位置高都相同，但是液体密度不同，所以压强水头就不相等，则压强不相等。

2-7.两容器内各点压强增值相等，因为水有传递压强的作用，不会因位置的不同压强的传递有所改变。

当施加外力时，液面压强增大了Ap∆，水面以下同一高度的各点压强都增加Ap∆。

2-8.（1）各测压管中水面高度都相等。

（2）标注如下，位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。

因为水作用面的面积不相等，而且作用面的形心点压强大小不同。

《⽔⼒学》题集1-3章答案第⼀章绪论第⼀题、选择题1、理想液体就是( B )(A)没有切应⼒⼜不变形得液体; (B)没有切应⼒但可变形得⼀种假想液体;(C)切应⼒与剪切变形率成直线关系得液体;(D)有切应⼒⽽不变形得液体。

2、理想液体与实际液体最主要得区别就是( D )A.不可压缩;B.不能膨胀; B.没有表⾯张⼒; D.没有粘滞性。

3、⽜顿内摩擦定律表明,决定流体内部切应⼒得因素就是( C )A动⼒粘度与速度B动⼒粘度与压强C动⼒粘度与速度梯度D动⼒粘度与作⽤⾯积4、下列物理量中,单位有可能为m2/s得系数为( A )A、运动粘滞系数B、动⼒粘滞系数C、体积弹性系数D、体积压缩系数6、影响⽔得运动粘度得主要因素为( A )A、⽔得温度;B、⽔得容重;B、当地⽓压; D、⽔得流速。

7、在⽔⼒学中,单位质量⼒就是指( C )A、单位⾯积液体受到得质量⼒B、单位⾯体积液体受到得质量⼒C、单位质量液体受到得质量⼒D、单位重量液体受到得质量⼒8、某流体得运动粘度v=3×106m2/s,密度ρ=800kg/m3,其动⼒粘度µ为( B )A、3、75×109Pa·sB、2、4×103Pa·sC、2、4×105Pa·sD、2、4×109Pa·s第⼆题、判断题1、重度与容重就是同⼀概念。

(√)2、液体得密度ρ与重度γ不随温度变化。

(×)3、⽜顿内摩擦定律适⽤于所有得液体。

(×)4、黏滞⼒随相对运动得产⽣⽽产⽣,消失⽽消失。

(√)5、⽔得粘性系数随温度升⾼⽽减⼩。

(√)7、⼀般情况下认为液体不可压缩。

(√)8、液体得内摩擦⼒与液体得速度成正⽐。

( ×)9、⽔流在边壁处得流速为零,因此该处得流速梯度为零。

( × )10、静⽌液体有粘滞性,所以有⽔头损失。

( × )12、表⾯张⼒不在液体得内部存在,只存在于液体表⾯。

第二章2.1 “恒定流与非恒定流”，“均匀流与非均匀流”，“渐变流与急变流”等三个概念是如何定义的？它们之间有么联系？渐变流具有什么重要的性质？ 恒定流：如果在流场中任何空间点上所有的运动要素都不随时间而改变，这种水流称为恒定流。

非恒定流：如果在流场中有任何一个运动要素是随时间而改变的，这种水流称为非恒定流。

均匀流：当水流的流线为相互平行的直线时，该水流称为均匀流。

非均匀流：当水流的流线不是相互平行的直线，该水流称为非均匀流。

渐变流：当水流的流线虽然不是相互平行直线，但几乎近于平行直线时称为渐变流。

急变流：当水流的流线之间的夹角很大或流线的曲率很小，这种水流称为急变流。

联系：恒定流和非恒定流均可以是均匀流或非均匀流，非均匀流中又包括渐变流和急变流。

渐变流具有的重要性质：过水断面上的压强近似服从静水压强分布：2.2 图（a ）表示一水闸正在提升闸门放水，图（b ）表示一水管正在打开阀门放水，若它们的上游水位均保持不变，问此时的水流是否符合A 1V 1＝AaVa 的连续方程？为什么？图2.2否，因水流均属非恒定流p z c g ρ+=2.3 能量方程中各项的几何意义和能量意义是什么？（1）各项的几何意义：从几何观点，式中 分别为位置水头、压强水头、流 速水头和两断面间的水头损失。

（2） 各项的能量意义： 分别代表单位重量液体的 平均位能、平均压能、平动能和能量损失。

2.4 关于水流去向问题，曾有以下一些说法如“水一定是从高处向低处”，“水是由压力大的地方向压力小的地方流”，“水是由流速大的地方向流速小的地方流”这些说法对吗？试用基本方程式论证说明。

都不对。

由能量方程知：任一断面的总机械能是由位能、压能和动能三部分组成的，它们间可相互转化，但不能分割。

水流总是从总机械能大的1-1断面流向总机械能小的2-2断面，其差值用来克服两断面间的总水头损失。

2.5 什么叫总水头线和测压管水头线？水力坡度和测压管坡度？均匀流的测压管水头线和总水头线的关系怎样？各断面总能量值 连接起来的曲线或直线称总水头线，把各断面的 值的点连接起来的线称测压管水头线。

第二章:水静力学 一：思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答：水头是压强的几何意义表示方法，它表示h 高的水头具有大小为ρgh 的压强。

绝对压强预想的压强是按不同的起点计算的压强，绝对压强是以0为起点，而相对压强是以当地大气压为基准测定的，所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压，即真空。

某点负压大小等于该点的相对压强。

Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中，z 表示某点在基准面以上的高度，称为位置水头，g p ρ表示在该点接一根测压管，液体沿测压管上升的高度，称为测压管高度或压强水头，g p z ρ+称为测压管水头，即为某点的压强水头高出基准面的高度。

关系是：（测压管水头）=（位置水头）+（压强水头）。

2-5.等压面是压强相等的点连成的面。

等压面是水平面的充要条件是液体处于惯性坐标系，即相对静止或匀速直线运动的状态。

2-6。

图中A-A 是等压面，C-C,B-B 都不是等压面，因为虽然位置高都相同，但是液体密度不同，所以压强水头就不相等，则压强不相等。

2-7.两容器内各点压强增值相等，因为水有传递压强的作用，不会因位置的不同压强的传递有所改变。

当施加外力时，液面压强增大了Ap∆，水面以下同一高度的各点压强都增加Ap∆。

2-8.（1）各测压管中水面高度都相等。

（2）标注如下，位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。

因为水作用面的面积不相等，而且作用面的形心点压强大小不同。

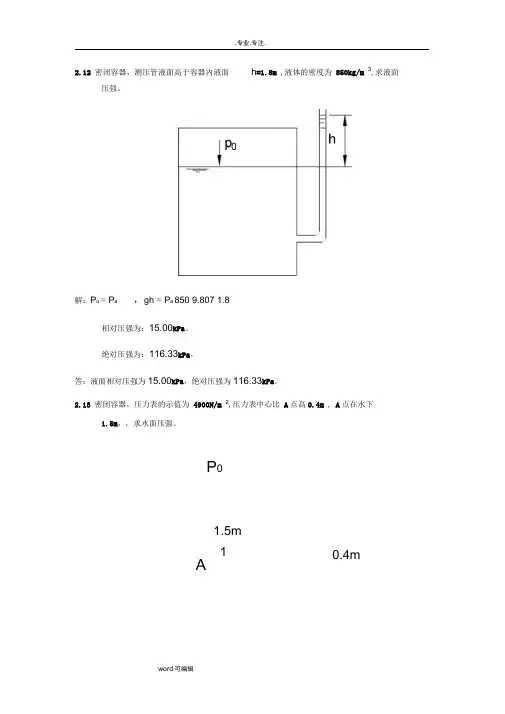
2.12 密闭容器，测压管液面高于容器内液面h=1.8m ,液体的密度为850kg/m 3,求液面压强。

解：P o = P a ，gh = P a 850 9.807 1.8相对压强为：15.00kPa。

绝对压强为：116.33kPa。

答：液面相对压强为15.00kPa，绝对压强为116.33kPa。

2.13 密闭容器，压力表的示值为4900N/m 2,压力表中心比A点高0.4m , A点在水下1.5m，，求水面压强。

P01.5m10.4mA解: P0 = P a P -1.1 'g二P a 4900 -1.1 1000 9.807二p a「5.888 （kPa）相对压强为：_5.888kPa。

绝对压强为：95.437kPa。

答: 水面相对压强为-5.888kPa,绝对压强为95.437kPa。

3m解：（1）总压力：Pz=A p=4「g 3 3 = 353.052 （kN）（2）支反力：R 二W总二W K W箱二W箱;?g 1 1 1 3 3 3=W箱 9807 28 =274.596 kN W箱不同之原因：总压力位底面水压力与面积的乘积，为压力体Qg。

而支座反力与水体重量及箱体重力相平衡，而水体重量为水的实际体积Eg。

答：水箱底面上总压力是353.052kN，4个支座的支座反力是274.596kN。

2.14 盛满水的容器，顶口装有活塞A，直径d =0.4m，容器底的直径D=1.0m，高h=1.8m ,如活塞上加力2520N （包括活塞自重），求容器底的压强和总压力解: （1）容器底的压强：P D =P A'gh =252°9807 1.8 =37.706（kPa）（相对压强）/-d24（2）容器底的总压力：P D二Ap D D2 p D12 37.706 10 = 29.614（kN）4 4答：容器底的压强为37.706kPa，总压力为29.614kN 。

2.6用多管水银测压计测压，图中标高的单位为m，试求水面的压强P0。

选择题（单选题）2.1 静止流体中存在：（a ）（a ）压应力；（b ）压应力和拉应力；（c ）压应力和剪应力；（d ）压应力、拉应力和剪应力。

2.2 相对压强的起算基准是：（c ）（a ）绝对真空；（b ）1个标准大气压；（c ）当地大气压；（d ）液面压强。

2.3 金属压力表的读值是：（b ）（a ）绝对压强；（b ）相对压强；（c ）绝对压强加当地大气压；（d ）相对压强加当地大气压。

2.4 某点的真空度为65000Pa ，当地大气压为0.1MPa,该点的绝对压强为：（d ）（a ）65000Pa ；（b ）55000Pa ；（c ）35000Pa ；（d ）165000Pa 。

2.5 绝对压强abs p 与相对压强p 、真空度V p 、当地大气压a p 之间的关系是：（c ）（a ）abs p =p +V p ；（b ）p =abs p +a p ；（c ）V p =a p -abs p ；（d ）p =V p +V p 。

2.6 在密闭容器上装有U 形水银测压计，其中1、2、3点位于同一水平面上，其压强关系为：（c ）（a ）1p >2p >3p ；（b ）1p =2p =3p ；（c ）1p <2p <3p ；（d ）2p <1p <3p 。

2.7 用U 形水银压差计测量水管内A 、B 两点的压强差，水银面高差h p =10cm, A p -B p 为：（b ）（a）13.33kPa；（b）12.35kPa；（c）9.8kPa；（d）6.4kPa。

2.8露天水池，水深5 m处的相对压强为：（b）（a）5kPa；（b）49kPa；（c）147kPa；（d）205kPa。

2.9垂直放置的矩形平板挡水，水深3m，静水总压力P的作用点到水面的距离Dy为：（c）（a）1.25m；（b）1.5m；（c）2m；（d）2.5m。

2.10圆形水桶，顶部及底部用环箍紧，桶内盛满液体，顶箍与底箍所受张力之比为：（a）（a）1/2；（b）1.0；（c）2；（d）3。

1 2 6 11答案在作业本2.12 （注：书中求绝对压强）用多管水银测压计测压，图中标高的单位为m ,试求水面的压强2-12形平板闸门倾角=45，闸门上缘A 处设有转轴，忽略闸门自重及门轴摩擦力，试求开启 闸门所需拉力T 。

P 4 3.0 1.4 g P 5 2.5 1.4 Hg g3.0 1.4 gP a 2.3 1.2Hg g2.5 1.2g 2.5 1.4Hg g3.0 1.4P a2.3 2.5 1.2 1.4 Hg g2.53.0 1.2 1.4 gP a 2.3 2.5 1.2 1.4 13.62.53.0 1.2 1.4 ggP a265.00 (kPa )gP o 265.00kPa 。

解：P oP o △ 3.0△ 1.4p o。

答：水面的压强 AB ，一侧挡水，已知长l=2m ，宽b=1m ，形心点水深h °=2m ,—A /1/bBa〈/1 /‘ /、尸⑵图解法。

心压强分市如图所示’和=屁—一刃旗兰 =12,68 (kPa)彳V_丿| •t-h-vVvX-vx-k 2 J解：（1）解析法P c A h e g bl 1000 9.807 2 1 239.228 （ kN ）bl 3y CV C A sin12blsin2.2 2122.946对A 点取矩，当开启闸门时，拉力厂满足’门户（打―儿）一丁1A 6 Pl p[P y D222sin45o12 2 sin 45oI C6S0 I- 9= 31.007 （规 P当TX3LOO7込时，可以开启闸门…詈曲+”•朴2化珈3（凶.对A点取矩，有£卑-/D]—丁*事8詔誓=帖l-co^45v12.68 xlxl+(26.55-12,68)x1cos 45°= 31.009 CkN) * 密开启闸门所需拉力r =31.009 kN0 ,2-13矩形闸门高h=3m,宽b=2m,上游水深h i=6m，下游水深h2=4.5m,试求:（1）作用在闸门上的静水总压力；（2）压力中心的位置。

第一章绪论第一题、选择题1.理想液体是( B )(A)没有切应力又不变形的液体；(B)没有切应力但可变形的一种假想液体；(C)切应力与剪切变形率成直线关系的液体；(D)有切应力而不变形的液体。

2.理想液体与实际液体最主要的区别是（D ）A．不可压缩；B．不能膨胀；B．没有表面张力；D．没有粘滞性。

3.牛顿内摩擦定律表明，决定流体内部切应力的因素是（C ）A动力粘度和速度B动力粘度和压强C动力粘度和速度梯度D动力粘度和作用面积4.下列物理量中，单位有可能为m2/s的系数为（A ）A. 运动粘滞系数B. 动力粘滞系数C. 体积弹性系数D. 体积压缩系数6.影响水的运动粘度的主要因素为（ A ）A.水的温度；B.水的容重；B.当地气压； D.水的流速。

7.在水力学中，单位质量力是指（C ）A、单位面积液体受到的质量力B、单位面体积液体受到的质量力C、单位质量液体受到的质量力D、单位重量液体受到的质量力8.某流体的运动粘度v=3×10-6m2/s，密度ρ=800kg/m3，其动力粘度μ为( B )第二题、判断题1.重度与容重是同一概念。

（√）2.液体的密度ρ和重度γ不随温度变化。

（×）3.牛顿内摩擦定律适用于所有的液体。

（×）4.黏滞力随相对运动的产生而产生，消失而消失。

（√）5.水的粘性系数随温度升高而减小。

（√）7.一般情况下认为液体不可压缩。

（√）8.液体的内摩擦力与液体的速度成正比。

（×）9.水流在边壁处的流速为零，因此该处的流速梯度为零。

（×）10.静止液体有粘滞性，所以有水头损失。

（×）12.表面张力不在液体的内部存在，只存在于液体表面。

（√）13.摩擦力、大气压力、表面张力属于质量力。

（×）第三题、填空题2.水力学中，连续介质模型是假设液体是一种连续充满其所占据空间毫无空隙的连续体。

3.在水力学中常常出现的液体主要物理性质有重度和粘性，在某些情况下还要涉及液体的压缩性、表面张力和汽化压强等。

2-1 解：（1）p A+γ水·ΔH=γH·Δh；所以p A=γH·Δh-γ水·ΔH=38.02kP a（γH=13.6γ水）（2）测压管长度：p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3 解：P A-γh=p B-γ(h1+h2+h)+γH h1所以，p A-p B=γH h1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解：p A=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kp a 2-7 解：（1）左支：绝对：p c'=p0'+γh0=86.5+9.8×2=106.1kPa（2）右支：p c'=p a+γ水h；h=（p c'-p a）/γ水=（106.1-9.8）/9.8=0.827m 2-8 解：p A=0.6p a=0.6×98=58.8kp a（1）左支：p A=γh1 h1=p A/γ=58.8/9.8=6m（2）右支：p A+γh=γH h2 h2=（p A+γh）/γH=0.456m2-10解：设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=9.8×0.6=5.886kp a2-12解：(1)设容器底部面积为S，相对压强为P，对容器底部进行受力分析：由牛顿第二定律：ΣF=m·a；-（P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知a/g-1=0a=g=9.8m/s2时，p=02-142-16解：下游无水时，h1=1.2m，h2=1.85m，b=3m（1）求静水总压力P方法10：P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+1.85)×2.14×3=133.7kN方法20：P=γh c A=γ(h1+h2/2)×AB×b=133.7kN（2）计算P的作用点D的位置：e=l/3·（2h1+h2ˊ）/（h1+h2ˊ）=0.915m（其中hˊ=h1+h2）（3）计算T:因为ΣM a=0 则：P·AC+G·AO·cos600 其中：AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以T=158kN下游有水时，AB=2.14,b=3m，p A=γh1=9.8×1.2=11.76kPa，p A=p B (1)静水总压力P左=γ·h c1A1=9.8×(h1+h2/2）×AB×b=P1=133.7kN （其中h c1=h1+h2/2 A1=AB×b）e1=0.915mP右=γ·h c2A2=9.8×h2/2×AB×b=P2=58.2kN（其中h c2=h2/2）e2=l/3=2.14/3=0.71m（2）因为ΣM a=0P1×(AB-e1）+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知：H=3m,b=5m,R=4.3m,θ=450 求P 及作用点 H=Rsin450=4.3×22=3m (1)水平分力：P x =γh e A x =9.8×1.5×3×5=220.5(KN) (2)铅垂分力：P z =γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中：Ω=S 梯OABC —S 扇OAC =8.4－7.257=1.143㎡ S 梯OABC =0.5×[4.3+（4.3-3）]×3=8.4㎡ S 扇OAC =360450πR 2=360450×3.14×4.32=7.257㎡ （3）P=PPzx22+=01.565.22022+=227.5（KN ）（4）P 与水平面的夹角α： α=arctanPPxz =arctan5.22001.56=14.250=14015` 2-192-20 解:已知b=10m ，k=8m（1）夹角计算：Sin β1=（173-170）/8=3/8=0.375（cos β1=550.5/8）β1=22.020Sin β2=（170-165）/8=5/8=0.625（cos β2=0.781） β2=38.680（2）水平方向水压力P x :(闸门宽b=10m)公式：P x =γh c A x =9.8×4×8×10=3136kN（另法：P x =1/2×9.8×8×8×10=31363136kN ）（3）垂直方向水压力P z =γV关键计算压力体体积V=[三角形ofc （11.12㎡）+扇形ocd （33.88㎡）-梯形ofed （34.36）]×b所以 V=（11.12+33.86-34.36）×10=10.636×10=106.36m ³P z =γV=9.8×106.36=1042.33kN（4）总压力P:P=(P x 2+P z 2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.51P 与水平面夹角17.510，且过o 点。

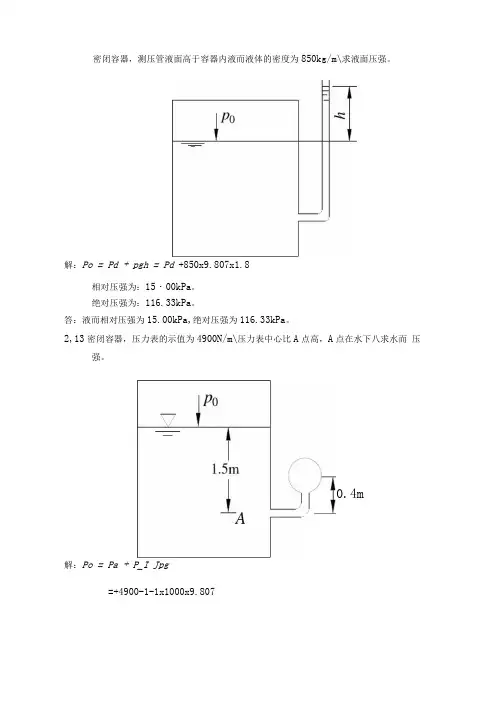
密闭容器，测压管液面高于容器内液而液体的密度为850kg/m\求液面压强。

解：Po = Pd + pgh = Pd +850x9.807x1.8相对压强为：15・00kPa。

绝对压强为：116.33kPa。

答：液而相对压强为15.00kPa,绝对压强为116.33kPa。

2,13密闭容器，压力表的示值为4900N/m\压力表中心比A点高，A点在水下八求水而压强。

0.4m解：Po = Pa + P_I Jpg=+4900-1-1x1000x9.807=Pa —5.888 (kPa)相对压强为：-5.888kPa 。

绝对压强为：95.437 06 答：水而相对压强为-5.888kPa. 绝对压强为95.437 kPa 。

解：（1）总压力:（2）支反力: 不同之原因: & = A ・p = 4pg X3X3 = 353,052 (kN) R = %=林+%=%+Qg(lxlxl + 3x3x3)=1绻 +9807 x28 = 274.596 kN +%总压力位底面水压力与面积的乘枳，为圧力体XQg 。

而支座反力与水体 重量及箱体重力相平衡，而水体重量为水的实际体积XQg 。

答：水箱底面上总压力是353.052kN. 4个支座的支座反力是274.596kNO2.14盛满水的容器，顶口装有活塞A.宜径dr 容器底的直径D G 高hr 如活塞上加 力2520N（包括活塞自重），求容器底的压强和总压力。

3m Im解：(1)容器底的压强:Pn = P A +pgh = 25^ + 9807xl.8 = 37.706 (kPa)(相对压强)(2)容器底的总压力:pQ = App =^D~ -Po = -^XI"X37.706x 10^ = 29.614 (kN) 答：容器底的压强为37.706kPa,总圧力为29・614kN。

用多皆水银测压计测圧，图中标髙的单位为m,试求水而的压强po。

Po v3.0_yL4隶解^ 〃0=久-(3・0-1・4)必=p5+(2・5-14)%g-(3・0-l ・4)Qg =Pa +(2・3-l ・2)%g-(2・5-l ・2)Qg+(2・5-l ・4)%g-(3・0-14)Qg=化+(2・3+2・5-1・2-14)乐 g-(2・5+3・0 - L2-14)Qg = N+[(2・3 + 2・5-l ・2-l ・4)xl3・6-(2・5 + 3・0-l ・2-l ・4)Qg]Qg=几+265.00 (kPa)答：水而的压强Po=265・OOkPa 。

第二章水静力学1、相对压强必为正值。

( )2、图示为一盛水容器。

当不计瓶重时, 作用于地面上的力等于水作用于瓶底的总压力。

( )3、静水总压力的压力中心就是受力面面积的形心。

( )4、二向曲面上的静水总压力的作用点就是静水总压力的水平分力与铅直分力的交点。

( )5、一个任意形状的倾斜平面与水面的夹角为。

则该平面上的静水总压力P=gy D A sin。

(y D为压力中心D的坐标，为水的密度，A 为斜面面积) （）6、图示为二块置于不同液体中的矩形平板，它们的宽度b，长度L及倾角均相等，则二板上的静水总压力作用点在水面以下的深度是相等的。

( )7、作用于两种不同液体接触面上的压力是质量力。

( )8、静水压强仅是由质量力引起的。

( )9、在一盛水容器的侧壁上开有两个小孔A、B，并安装一 U 形水银压差计，如图所示。

由于A、B两点静水压强不等，h 的差值。

( )10、物体在水中受到的浮力等于作用于物体表面的静水总压力。

( )11、选择下列正确的等压面: ( )C (4)D D( )(1) 淹没面积的中心； (2) 压力体的中心；(3) 总压力的作用点；(4) 受压面的形心。

13、平衡液体中的等压面必为( )(1) 水平面； (2) 斜平面； (3) 旋转抛物面； (4) 与质量力相正交的面。

14、图示四个容器内的水深均为H，则容器底面静水压强最大的是( )(1) a ; (2) b ; (3) c ; (4) d 。

15、欧拉液体平衡微分方程 ( ) (1) 只适用于静止液体； (2) 只适用于相对平衡液体；(3) 不适用于理想液体； (4) 理想液体和实际液体均适用。

16、容器中盛有两种不同重度的静止液体，如图所示，作用在容器A B 壁面上的静水压强分布图应为 ( ) (1) a (2) b (3) c (4) d17、液体某点的绝对压强为 58 kP a，则该点的相对压强为 ( )(1) 159.3 kP a； (2) 43.3 kP a； (3) -58 kP a (4) -43.3 kP a。

水力学第二章课后答案篇一：水力学第二章答案(吕宏兴__裴国霞等)2-1 解：（1）pA+γ水·ΔH=γH·Δh；所以pA=γH·Δh-γ水·ΔH=38.02kPa（γH=13.6γ水）（2）测压管长度：pA=γ水·h 所以h= pA/γ水=38.02×103/9.8×103=3.88m2-3 解：PA-γh=pB-γ(h1+h2+h)+γHh1所以，pA-pB=γHh1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解：pA=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kpa2-7 解：（1）左支：绝对：pc =p0 +γh0=86.5+9.8×2=106.1kPa（2）右支：pc =pa+γ水h；h=（pc -pa）/γ水=（106.1-9.8）/9.8=0.827m2-8 解：pA=0.6pa=0.6×98=58.8kpa（1）左支：pA=γh1 h1=pA/γ=58.8/9.8=6m（2）右支：pA+γh=γHh2 h2=（pA+γh）/γH=0.456m2-10解：设管嘴内的绝对压强为p ,则p +γh= paPv=pa- p =γh=9.8×0.6=5.886kpa2-12解：(1)设容器底部面积为S，相对压强为P，对容器底部进行受力分析：由牛顿第二定律：ΣF=m·a；-（P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)篇二：《水力学》第二章答案第二章:水静力学一：思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答：水头是压强的几何意义表示方法，它表示h高的水头具有大小为?gh的压强。

2.12 密闭容器，测压管液面高于容器内液面h =1.8m ，液体的密度为850kg/m 3，求液面压强。

解：08509.807 1.8a a p p gh p ρ=+=+⨯⨯相对压强为：15.00kPa 。

绝对压强为：116.33kPa 。

答：液面相对压强为15.00kPa ，绝对压强为116.33kPa 。

2.13 密闭容器，压力表的示值为4900N/m 2，压力表中心比A 点高0.4m ，A 点在水下1.5m ，，求水面压强。

解：0 1.1a p p p g ρ=+-5.888a p =-（kPa ）相对压强为： 5.888-kPa 。

绝对压强为：95.437kPa 。

答：水面相对压强为 5.888-kPa ，绝对压强为95.437kPa 。

解：（1）总压力：433353.052Z P A p g ρ=⋅=⨯⨯=（kN ） （2）支反力：()111333R W W W W g ρ==+=+⨯⨯+⨯⨯总水箱箱980728274.596W =+⨯=箱kN W +箱不同之原因：总压力位底面水压力与面积的乘积，为压力体g ρ⨯。

而支座反力与水体重量及箱体重力相平衡，而水体重量为水的实际体积g ρ⨯。

答：水箱底面上总压力是353.052kN ，4个支座的支座反力是274.596kN 。

2.14 盛满水的容器，顶口装有活塞A ，直径d =0.4m ，容器底的直径D =1.0m ，高h =1.8m ，如活塞上加力2520N （包括活塞自重），求容器底的压强和总压力。

解：（1）容器底的压强：225209807 1.837.7064D A p p gh dρπ=+=+⨯=（kPa ）（相对压强） （2）容器底的总压力：223137.7061029.61444D D D P Ap D p ππ==⋅=⨯⨯⨯=（kN ）答：容器底的压强为37.706kPa ，总压力为29.614kN 。

2.6用多管水银测压计测压，图中标高的单位为m ，试求水面的压强0p 。

答案说明以下答案是由老师自己做出来的，其中的每一题的画图都省略了，希望同学们自己在做题过程中补充上完整的图形。

在答案电子话过程中可能会有一些错误，希望同学们可多提宝贵意见。

第二章作业答案2-91(1.5 1.0)53.9ap p g p kpa 11151.9absap p p kpa 20(1.50.5)58.8ap p g p kpa22156.8abs a p p p kpa 12126.5p p Z Z mg g2-11 略2-12(2.50.9)(2.00.9)(2.00.7)(1.80.7)0HgHgp g g g g 0265p kpa2-14 受压面为矩形平面76.38c Pgh kN34112cb a J m 289cDccJ y y y 所以，作用点至A 点的距离10'29Dy y 根据合力矩守恒2cos 60'84.9oT P y TkN2-18cP gh (sin60)2146.5oa g H ab kNsin 60(cos60)ooTG G P f45.9T kN闸门的静水压强分布图为梯形，根据梯形的压力中心距底部距离的计算公式12122()3h h a eh h 21sinh H h Ha 1.13e m2-21仅考虑左侧水：11144.1x c x P gh kN （）1134.6z P gV kN（）仅考虑右侧水22211.03x c x P gh kN （）2217.32z P gV kN （）综合两侧水1233.08x x x P P P kN () 1217.32zz z P P P kN （）总压力22()37.34xyPP P kNtanZ xP P 2-23分析上半球xP 232[()]3ZP gVTn n g R H R R n第三章作业答案3-32max 00.0342max max00[(1())]1/20.212/rrQ udu d r u u r rL s0.075/Qvm s3-6根据连续性方程123Q Q Q 34/v m s3-7根据连续性方程123Q Q Q 23422231482.3370.58mm3-11 建立能量方程22111222121222122122()2.252hgpp v p v z z g gggz z p p vv h mgg油油油油油2.2551.1/Q K L s3-15在图上12d d 和断面建立能量方程2211122212122220p vp vz z g gggz z p 联立连续性方程1122v v 24.9/v m s在图自由液面和2d 断面建立能量方程221.232vHmg3-18建立能量方程22111222121212221.8 1.680p vp vz z g g ggz m z mp p 连续性方程12211.8(1.80.30.12)1.3v v v v 13111.23/5.98/v m s Qv m s3-20建立的坐标系比较特别，X 轴沿着1Q 方向，Y 轴与X 轴垂直根据能量方程可知1268.1/vv v m s建立动量方程，沿X 轴方向：11221212cos600cos60ooQ v Q v Q v Q Q Q Q Q Q连续性方程12(1cos60)2(1cos60)2ooQ Q Q Q 313225.05/8.35/Q m s Q m s建立动量方程，沿Y 轴方向：(sin60)1969oyR Q v N3-23在A-A ，B-B 断面间建立能量方程2.4/3.8/A bv m s v m s221112221212222175.7p vp vz z g gggz z p kN在A-A ，B-B 断面间建立动量方程沿X 轴方向：1cos60(cos 60)sin 60sin 60ooA AB B x B ooB B y B p v p v R Q v v p v R Qv 54555984y xR N R N3-24 （1）建立能量方程22121222vvh h gg连续性方程1122h v h v 3228.9215)998(vv 0294107232v vs m v /512.82mh v v h 762.15512.831212（2）以1-1断面和2-2断面之间的水体为控制体，并假设整个坝面对水体的水平反力为F 。

2-1 解:（1）卩*7木・AH=Y H・ Ah：所以P A=V H• Ah・Y** AH二（V H=Y木〉（2）测压管长度：pA=v木• h所以h= P A/Y杆 X ICP/X 10^=3.88m 2-3 解：pA-vh=PB-V(hi+h2+h)+VHhi所以，P A・P B=VMhi-v(hi+h2)=XX2-6•水I h3 Id解:pA=VH（hi+h2）-v（hi+h2）=X XXX 解: （1）左支:绝对:pc-po'+vho=+ X 2=（2）右支: T h l 丄pc=pa+Y h=（Pc'-Pa）/v （）/=0.827m 2-8 解：PA==X98=2-10(1)左支J pA=vhi hi=pA/v==6m(2)右支J pA+Yh=VMh2 h2= (pA+yh)/VM=0.456m解：设管嘴内的绝对压强为眄则P "+Vh=paPv=pa- p-vh= X=2-12解:(1)设容器底部面枳为S,相对压强为P,对容器底部进行受力分析: 由牛顿第二泄律：2F=rn • a： - (P+G)=-m • a 所以得出P • s+v • s • h=p • s • h • ap=p • h • a -vh=Yh/g • a-yh=yh{a/g-l)p=X2=nV(2)相对压强为0 p=vh(l-a/g)=O由式可知a/g-l=Oa=g=9.8m/s^ 时，pR2-14(d) 2-16下游无水时，hi=» h2=r b=3m（1）求静水总压力P方法 1。

: P=Qb=]^[vhi+v{hi+h2)]XABXb=lZ2XX(2X +X X3=方法2° : P=yhcA=v(hi+h2Z2)XABXb=///ZB //// （2） i|•算P 的作用点D 的位置:e=l^ • (2hi+h2 ' ) / (hi+hz " ) =0.915m (英中 h " =hi+h2)(3) 计算T:因为2Ma=0贝Ij ：P • AC+G • AO • cos60° 夷中 j AC=AB-e=下游有水时，ABsb=3m, pA=vhi=X=, papBhlh2 r*lil ・oh3AO=AB/2GX 所以 T=158kN⑴静水总压力P v=V • hciAi=X{hi+h2Z2) XABXb=Pi=(其中 hci=hi+h2/2 Ai=ABX b) ei=P 沪V • hc2A2= Xhz/ZXABXb=p2=(其中入2比2介)e2=l^=3=0,71m(2)因为 SlVla=OPl X {AB-ei) +GXAOX cos60^=T XABX cosGO^+Pz X (AB-ez)T=已知：H=3m,b=5m,R=,e=45'^求P及作用点H=Rsin45°=X—=3m2(1) 水平分力：Px=yheAx=XX3X5=(KN)(2) 铅垂分力：Pz=vv=vfiXb=X X5=(KN) 苴中 J O=S »OABC —S ttOAC= —= m* SwoAK=x[+ O ]X3二nV s A oAc= 45 n R2二 45 X x=nVW — ⑶+ P 〉j220・52 + 56・0f= (KN )(4) s，卩与水平而的夹角a : P 56.01 …a =arctan^^=arctan ------ ==14°15'Px 220.5Pz360"2-19(a)(b)2-20 解:已知b=10m» k=8m（1）夹角计算:Sinpi= (173-170) /8=d^= (cosR尸8) pi=Sinp2= f 170-165) /8=5/8= (cosp2=) p2=（2）水平方向水压力P*（闸门宽b=10m）公式：Px=vhcAx= X 4 X 8 X 10=3136kN(列法J Px=l?2XX8X8X10=kN)(3)垂直方向水压力P Z=Y V关键汁算压力体体枳V可三角形ofc (mO +扇形ocd (nV)・梯形ofed () ]Xb所以 V= ( + ) X10=X10=10636mPi=VV= X =(4)总压力P:P=(Px^+Pz^)=作用方向U ==P与水平而夹角，且过o点。