(完整版)通信电子线路习题解答
- 格式:pdf
- 大小:319.02 KB
- 文档页数:15



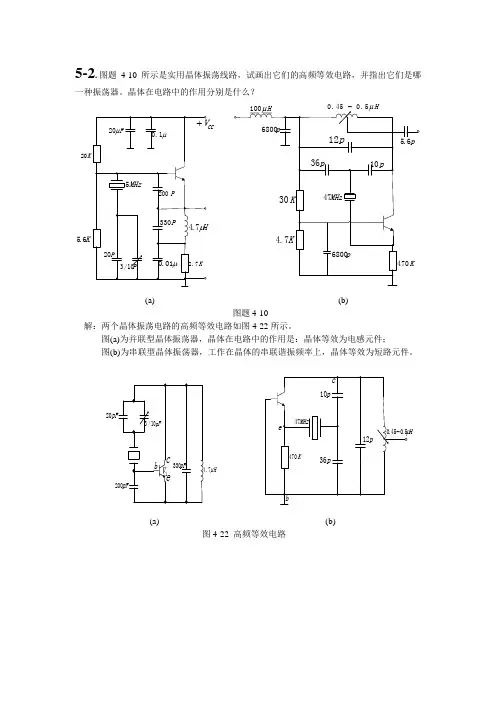
5-2.图题4-10所示是实用晶体振荡线路,试画出它们的高频等效电路,并指出它们是哪一种振荡器。
晶体在电路中的作用分别是什么?K20K6.5(a) (b)图题4-10解:两个晶体振荡电路的高频等效电路如图4-22所示。
图(a)为并联型晶体振荡器,晶体在电路中的作用是:晶体等效为电感元件;图(b)为串联型晶体振荡器,工作在晶体的串联谐振频率上,晶体等效为短路元件。
20Hμ7.H(a) (b)图4-22 高频等效电路5-5晶体振荡电路如图P4.12所示,试画出该电路的交流通路;若1f 为11C L 的谐振频率,2f 为22C L 的谐振频率,试分析电路能否产生自激振荡。
若能振荡,指出振荡频率与1f 、2f 之间的关系。
图P4.12 解:该电路的简化交流通路如图P4.12(s)所示,图P4.12(s)电路可以构成并联型晶体振荡器。
若要产生振荡,要求晶体呈感性, 11C L 和22C L 呈容性。
必须满足12f f f osc >>。
5-6 图示为三回路振荡器的等效电路,设有以下四种情况:①332211C L C L C L >>; ②332211C L C L C L <<; ③332211C L C L C L >=; ④332211C L C L C L =<。
试分析上述四种情况是否可能振荡?振荡频率0f 与回路谐振频率有何关系?1L 2L 3L图题4-5解:设11C L 回路谐振频率为11011C L =ω,22C L 回路谐振频率为22021C L =ω,33C L 回路谐振频率为33031C L =ω。
能满足振荡的相位条件是be ce X X ,同电抗性质,cb X 与be ce X X ,反性质。
①332211C L C L C L >> 可知321f f f f osc <<<若振荡频率满足321f f f f osc <<<条件,则11C L 回路等效为容抗、22C L 回路等效为容抗,而33C L 回路等效为感抗,满足相位条件,可能振荡。

第2章2-3 已知串联谐振回路的谐振频率f 0=30MHz ,电容C =80pF ,谐振阻抗R 0=5Ω,试求:电感L 和回路品质因数Q 0。
解:1、求L 根据公式:LC10=ω得:H H CL μ≈⨯⨯⨯⨯π=ω=-35.010********1126222、求Q 0根据公式:Q 0 = 1/(ω0CR 0) =ω0L/R 0得:Q 0==1/(ω0CR 0) =1/(2π×30×106×80×10-12×5)=1/(24π×10-3)≈ 13. 27 或:Q 0==ω0L/R 0 =(2π×30×106×0.35×10-6)/5≈ 13. 202-5 题图2-5是单调谐放大器的交流通路,当谐振频率等于10MHz 时,测得晶体管的Y 参数为:y re =0;y ie =2+j0.5 (mS); y fe =20+j5 (mS);y oe =20+j40 (μS)。
放大器的通频带为300kHz ,谐振电压增益为50,试求:电路元件C 、L 的参数值。
题图2-5解:已知P 1=1,P 2=1,f 0=10MHz ,B=2Δf 0.7=300 kHz ,500=u A 根据∑-=g y p p A fe u 210 ,∑-=g y p p A fe u 210 得: mS A y g u fe 41.050520220≈+==∑ 根据QfQ 2B 00=πω=得:Q L = f 0/2Δf 0.7 =33.33 根据ω0C oe =40(μS)得:C oe =40×10-6/(2π×10×106)≈ 0.637pF ,根据ie 22oe 21C p C C p C ++=∑ 和C Σ = g ΣQ L /ω0得:C= C Σ-C oe ≈217.6-0.637 ≈217pF根据LC10=ω得:L ≈1.15μH2-8 如题图2-8所示。

通信电子电路课后练习题含答案一、选择题1.以下哪个式子描述了在电路中的欧姆定律?A. U = I / RB. U = I * RC. R = U * ID. I = R / U正确答案是A。
2.下列选项中哪个不是三个基本电子元件?A. 电阻B. 电感C. 二极管D. 晶体管正确答案是D。
3.在以下哪个材料中,电子的导电性最差?A. 银B. 铜C. 金D. 锡正确答案是D。
二、填空题1.在一个电路中,如果电流为10A,电阻为5欧姆,则电压为______。
正确答案为50V。
2.电感对于交流电流有一些特殊的性质。
一旦它获得了一个变化的电流源,则会产生一个________。
正确答案为磁场。
3.晶体管是一种_______,它具有放大和开关的功能。
正确答案为半导体。
三、计算题1.在所示的电路中,电压值为5V,电阻值为10欧姆。
求电流值。
电路图解:根据欧姆定律:I = U / R = 5V / 10Ω = 0.5A。
答案为0.5A。
2.在所示的电路中,电流值为20A,电阻值为5欧姆。
求电压值。
电路图解:根据欧姆定律:U = I * R = 20A * 5Ω = 100V。
答案为100V。
四、简答题1.什么是电容?它在电路中有什么作用?答:电容是一种元件,具有存储电荷的能力。
它在电路中的主要作用是滤波、储能、存储信息,同时也可以作为信号的耦合或解耦元件。
2.整流电路的作用是什么?它有哪些常见的形式?答:整流电路用于将交流电转换为直流电。
常见的整流电路形式有半波整流、全波整流和桥式整流。
五、答案一、选择题1.A2.D3.D二、填空题1.50V2.磁场3.半导体三、计算题1.0.5A2.100V。

第一章绪论习题指导思考题1.1.1能识别不同频率信号的元器件有哪些?1.1.2你知道信号在传输和处理中是如何利用“空分”、“频分”和“时分”来区分不同信号的实际例子吗?1.1.3若无线信道能容许通过带宽为无限的有用信号,则从频分的角度,我们能将这样的信号通过无线方式传输吗?为什么?思考题:1.2.1为了接收端能将收到的图1-2-5(d)所示信号按发送信号周期进行“同步分离”,接收端是否应该有一个与发端同步的标准“同步时钟信号”?1.2.2你知道有关利用“空分”、“频分”和“时分”理论来组成电路系统的实际例吗?1.2.3问:下列说法是否正确?图1-2-2(a)、(b)的数字信号和图1-2-3(a)的数字的模拟信号都具有时间上离散的携带信息特征;图1-2-2(c)的模拟基带信号具有时间上连续的携带信息特征。
思考题:1.3.1在输入有用信号带宽有限的情况下,为了减弱平均噪声对电路输出波带来的影响,电路的带宽是否应与输入有用信号带宽一致?为什么?思考题与练习题1-11-1实际通信信道有哪几种?电信道中的有线和无线信道中哪个更有利于接收电路对信号的识别?1-21-2多路通信中的频分复用和时分复用是否可以用同一功能电路来实现?举例说明。
(提示:参见图1-2-5和图1-3-1)1-31-3用于远距离发射的数字调制和模拟调制的输入和输出信号的差异如何?1-41-4对发送和接收电路的基本要求是什么?解:这里的发送设备是在保持信息不变的前提下,以基带信号为有效信号的信号变换电路,它涉及信号的调制、放大、滤波和发射等具体电路。
能使已调信号成为符合特定信道传输要求的信号形式,能实现在一个物理通道中的多路信号传输,并具有较好的信号抗干扰的潜在能力。
接收电路的基本要求是:在理想情况下,能从信道中提取出特定发射端输出的有用已调信号,并将此信号进行与发射端相反的信号处理,从而恢复原基带信号。
接受电路通常涉及小信号选频放大电路、混频器、中频放大器、解调电路等具体电路。

5-18 试说明石英晶体振荡器的频率稳定度为什么比较高?解答:石英晶体振荡器频率稳定度高的原因是:1、石英晶体的物理和化学性能都十分稳定,它的等效谐振回路有很高的标准性;2、在谐振频率附近,晶体的等效参数L q很大,C q很小,r q也不高,晶体的Q值可高达数百万量级。
3、在串、并联谐振频率之间很窄狭的工作频带内,具有极陡峭的电抗特性曲线,因而对频率变化具有极灵敏的补偿能力。
5-19 石英晶体振荡器的振荡频率基本上是由石英晶体的工作频率所决定,那么振荡回路的L、C参数是否可以随意选择?为什么?解答:不能。
L,C参数决定了电路的振荡频率。
石英晶体要么工作在感性区间,要么工作在它的串联谐振频率上,不能使用容性区。
如果振荡器电路设计在晶体呈现电容性时产生振荡,就不能保证频率稳定作用。
5-20 试说明影响振荡器相位平衡条件的主要因素,指明提高振荡器频率稳定度的途径。
解答:影响振荡器相位平衡条件的主要因素有:1、振荡回路参数L、C的变化。
2、回路品质因素Q值的影响。
3、有源器件参数变化的影响。
提高频率稳定度的途径有:1、减小外因变化,即减小温度、电源电压变化,采用恒温,稳压;减小湿度、大气压力,磁场感应,机械振动等影响,采用密封、屏蔽、减振等方法;减小负载的影响,采用射随隔离,松耦合等方式;2、提高回路标准性,采用优质器件;3、减小相角 YF及其变化量 YF,采用电容三端型电路。
5-21 振荡器的幅度不稳定,是否也会引起频率的不稳定,为什么?5-22 已知某广播发射机的主振电路如题图5-7所示,试求:(1) 画出交流等效电路;(2) 说明各主要元器件的作用;(3) 电路采用了哪几种稳频措施。
题图5-7解答:(1)等效电路如下图所示。
C 2C 1 300pF(2)采用的稳频措施有:① 二次稳压;②采用了恒温槽;③采用晶振电容三端电路;④采用10K 和1200p 形成松耦合,输出由下一级射随输出。
5-23画一个用运放电路组成的文氏电桥振荡电路,并说明图中各元件的作用。


复习题一、选择题1.二极管峰值包络检波器适用于哪种调幅波的解调(C)。
A 单边带调幅波B 抑制载波双边带调幅波C 普通调幅波D 残留边带调幅波2.欲提高功率放大器的效率,应使放大器的工作状态为(C)。
A 甲类B 乙类C 丙类3.变容二极管调频器实现线性调频的条件是变容二极管的结电容变化指数n为(C)。
A 1/3B 1/2C 2D 44.某超外差接收机的中频为465kHz,当接收550kHz的信号时,还收到1480kHz的干扰信号,此干扰为(B)。
A 干扰哨声B 镜像干扰C 互调干扰D 交调干扰5.某单频调制的普通调幅波的最大振幅为10v,最小振幅为6v,则调幅系数m a为(C)A 0.6B 0.4C 0.25D 0.16.以下几种混频器电路中,输出信号频谱最纯净的是(A)A 二极管混频器B 三极管混频器C 模拟乘法器混频器7.某丙类谐振功率放大器工作在临界状态,若保持其它参数不变,将集电极直流电源电压增大,则放大器的工作状态将变为(C)A 过压B 临界C 欠压8.鉴频的描述是( B )A 调幅信号的解调B 调频信号的解调C 调相信号的解调9.下图所示框图能实现何种功能? ( C )其中u s(t)= U s cosωs tcosΩt, u L(t)= U L cosωL tA 振幅调制B 调幅波的解调C 混频D 鉴频10.在超外差式调幅收音机中,混频器的输出谐振回路应调谐在什么频率上?( D )A 载波频率f cB 本机振荡频率f LC f c + f LD f c - f L11.图1所示的检波电路适于对哪种已调信号进行检波? ( C )A 抑制载波的双边带调幅波B 单边带调幅波C 普通调幅波D 调相波12.调频波的瞬时附加相位与什么成正比?( A )A 调制信号的积分B 调制信号的微分C 调制信号的瞬时值D 调制信号的频率13.在谐振功率放大器中,为了提高谐波抑制能力,谐振回路的Qe值(A)A越大越好B越小越好C无关14.为了实现丙类工作,基极偏置电压应设置在功率管的(B)A 放大区B 截止区C 饱和区15.某调频波,其调制信号频率F=1kHz,载波频率为10.7MHz,最大频偏Δf m=10kHz,若调制信号的振幅不变,频率加倍,则此时调频波的频带宽度为(B)A 12kHzB 24kHzC 20kHzD 40kHz16.双边带调制信号和单边带调制信号的载波被(C)A变频B搬移C抑制17.双边带调制信号和单边带调制信号的包络是否反映调制信号的变化规律。
K泛指传输电信号的导线,一般是对称的平行导线,或者扭在一起的双绞线等。
2、真正的无损传输线是不存在的,如果满足r « wl,g« wc则可以近似看做无损耗传输线。
4、86.6 Q5、当输入信号的频率变化时,无损传输线随输入信号频率的变化而不再是无损传输•:6题、(1)<20 =62.8(2)r r=3.9kQL是理想电感.7题、(1)容性 (2)容性8 题、H*o=141X10:rad/s二141BW=1.59X104H ZBo.讦15. 74X10*HzD 二0. 19题、vr o=1.15X10:rad/sR z =1.86 X105QQ 二 161.7BW•二 11324. THzBo. Fl 13247HzD二0・ 111题、BW•二0. 43 —Q12题、(1)几与人很接近:在f q<f<f p时,回路呈现容性。
(2)f p>f q ,在频率人处回路C短路状态,在频率几处回路处于开路状态。
:(3)/;,-/;=—f q2C°13题、临界或弱过压状态14、60° 〜80°15题、因为低频功率放大器是对信号相对带宽比较宽的信号(即宽带信号)进行放大,所以不能采用谐振回路(只能对单一信号选择性比较好)作为负载。
髙频功率放大器因苴信号的相对带宽很窄(即窄带信号)可以釆用谐振回路作为负载,所以可以工作在丙类。
16 题、(1) Po=6・336W , nc=84.5%(2)29.2V17题、(1)三极管的导通角变为60。
左右:(2)谐振回路Li和Ci的谐振频率应该变为原来的2 倍。
同时增加陷波电路,其谐振频率为基波频率。
18题、对角标注19题、(1)交流通路如图1:(2)电感三点式振荡器。
(3) 1.6X105H Z(4)CB作用,通交流,隔宜流。
图1CE作用,旁路电容。
20题、(1)交流通路如图2图2(2)电容三点式振荡器*(3) 3.2X10G Hzo(4)CB作用:交流零电位。
第1章绪论1.答:变换器(换能器):将被发送的信息变换为电信号。
例如话筒将声音变为电信号。
发射机:将换能器输出的电信号变为强度足够的、适合天线发射的高频电振荡信号。
天线:将高频电振荡信号转换成电磁波发射出去。
接收天线:从自由空间中接收各种电磁波并感生出高频已调电振荡信号。
接收机:将天线感生出的高频已调电振荡信号转换成携带有用信息的原始电信号。
变换器(换能器):将携带有用信息的原始电信号还原为所传送信息。
2.答:调制:由携有信息的电信号去控制高频振荡信号的某一参数,使该参数按照电信号的规律而变化。
调制有调幅、调频和调相三种方式。
若不经过调制,则会存在以下问题:(1)无法制造合适尺寸的天线;(2)接收者无法选出要接收的信号。
3.答:发射机实现方框图:接收机实现方框图:4.答:接收机的本地振荡频率为1401kHz或471kHz。
第2章 通信电子线路基础1.答:LC 并联谐振回路在谐振时呈纯电阻性,且纯电阻值最大。
2.答:1001011010211660000=⨯⨯⨯⨯⨯==-πωG LG Q ms .s .s L Q G 160101601011010210011366000=⨯=⨯⨯⨯⨯⨯==--πω 2561016011300..G R =Ω⨯==-KΩ LC f π210=()()2501025010110102861211262620=⨯=⨯⨯⨯⨯==--F F .L f C πpF3.答:高频晶体管Y 参数等效电路的适用条件是在高频小信号情况下。
第3章 高频小信号放大器1.答:高频小信号放大器若按器件分可分为晶体管放大器、场效应管放大器、集成电路放大器;若按通频带分可分为窄带放大器和宽带放大器;按照电路形式可分为单级和级联放大器;若按负载分可分为谐振放大器和非谐振放大器。
其质量指标有:电压增益;通频带;选择性;工作稳定性和噪声系数等。
2.答:由于放大器所放大的一般都是已调制的信号,已调制的信号都包含一定的频谱宽度,所以放大器必须有一定的通频带,以便让信号中的有用频谱分量通过放大器,所以通频带是小信号谐振放大器的一个重要指标。
思考题与习题2-1 列表比较串、并联调谐回路的异同点(通频带、选择性、相位特性、幅度特性等)。
表2.12-2 已知某一并联谐振回路的谐振频率f p =1MHz ,要求对990kHz 的干扰信号有足够的衰减,问该并联回路应如何设计?为了对990kHz 的干扰信号有足够的衰减,回路的通频带必须小于20kHz 。
取kHz B 10=,2-3 试定性分析题图2-1所示电路在什么情况下呈现串联谐振或并联谐振状态?题图2-1图(a ):22111111L C L C L oωωωωω-+-=图(b ):22111111C L C L C oωωωωω-+-=图(c ):22111111C L C L C oωωωωω-+-=2-4 有一并联回路,其通频带B 过窄,在L 、C 不变的条件下,怎样能使B 增宽?PoQ f B 2=, 当L 、C 不变时,0f 不变。
所以要使B 增宽只要P Q 减小。
而CLR Q pP =,故减小P R 就能增加带宽 2-5 信号源及负载对谐振回路有何影响,应如何减弱这种影响?对于串联谐振回路(如右图所示):设没有接入信号源内阻和负载电阻时回路本身的Q 值为o Q ,则:RLQ o o ω=设接入信号源内阻和负载电阻的Q 为L Q 值,则:RR R R Q R R R L Q Ls L++=++=1Ls o L ω 其中R 为回路本身的损耗,R S 为信号源内阻,R L 为负载电阻。
由此看出:串联谐振回路适于R s 很小(恒压源)和R L 不大的电路,只有这样Q L 才不至于太低,保证回路有较好的选择性。
对于并联谐振电路(如下图所示):设接入信号源内阻和负载电阻的Q 值为L Q由于没有信号源内阻和负载接入时的Q 值为由式(2-31)可知,当R s 和R L 较小时,Q L 也减小,所以对并联回路而言,并联的电阻越大越好。
因此并联谐振回路适于恒流源。
2-6 已知某电视机一滤波电路如题图2-2所示,试问这个电路对什么信号滤除能力最强,对什么信号滤除能力最弱,定性画出它的幅频特性。
思考题与习题2-1 列表比较串、并联调谐回路的异同点(通频带、选择性、相位特性、幅度特性等)。
表2.1·15··16·2-2 已知某一并联谐振回路的谐振频率f p=1MHz,要求对990kHz的干扰信号有足够的衰减,问该并联回路应如何设计?为了对990kHz的干扰信号有足够的衰减,回路的通频带必须小于20kHz。
取,kHzB10=100101===kHzMHzBfQ pp2-3 试定性分析题图2-1所示电路在什么情况下呈现串联谐振或并联谐振状态?12C2121题图2-1·17·图(a ):22111111L C L C L oωωωωω-+-=图(b ):22111111C L C L C oωωωωω-+-=图(c ):22111111C L C L C oωωωωω-+-=2-4 有一并联回路,其通频带B 过窄,在L 、C 不变的条件下,怎样能使B 增宽?, 当L 、C 不变时,不变。
所以要使B 增宽只要减小。
PoQ f B 2=0f P Q 而,故减小就能增加带宽CLR Q pP =P R 2-5 信号源及负载对谐振回路有何影响,应如何减弱这种影响?对于串联谐振回路(如右图所示):设没有接入信号源内阻和负载电阻时回路本身的Q 值为 ,o Q 则:RLQ o o ω=设接入信号源内阻和负载电阻的Q 为值,则:L QRR R R Q R R R LQ L s L++=++=1Ls o L ω其中R 为回路本身的损耗,R S 为信号源内阻,R L 为负载电阻。
由此看出:串联谐振回路适于R s 很小(恒压源)和R L 不大的电路,只有这样Q L 才不至于太低,保证回路有较好的选择性。
对于并联谐振电路(如下图所示):bega·18·IR s=s1gR p=s1gR L=LG1设接入信号源内阻和负载电阻的Q值为LQ⎪⎪⎭⎫⎝⎛++=++=pLpsppLsppL11)(1GGGGLGGGGLQωω由于没有信号源内阻和负载接入时的Q值为Lpsppppppp11RRRRQQGCLGQL++===故ωω由式(2-31)可知,当R s和R L较小时,Q L也减小,所以对并联回路而言,并联的电阻越大越好。
因此并联谐振回路适于恒流源。
2-6 已知某电视机一滤波电路如题图2-2所示,试问这个电路对什么信号滤除能力最强,对什么信号滤除能力最弱,定性画出它的幅频特性。
V1=V2?i题图2-2 题图2-32-7 已知调谐电路如题图2-3所示,回路的谐振频率为465kHz,试求:(1)电感L值;(2)L无损耗时回路的通频带;(3)L有损耗(Q L=100)回路的通频带宽度。
左侧电路的接入系数:25.040120401=+=TTTp·19·右侧电路的接入系数: 25.040120402=+=TT Tp 等效电源:s s i p i 1'=等效阻抗: Ω=Ω+Ω+Ω=k k p k k p R p 67.265.216011012221等效容抗: 2221'16?10p pF p pF C ⨯++⨯= 电容值未知2-8 回路的插入损耗是怎样引起的,应如何减小这一损耗?由于回路有谐振电阻R p 存在,它会消耗功率因此信号源送来的功率不能全部送给负载R L ,有一部分功率被回路电导g p 所消耗了,这就是插入损耗。
增大回路本身的Q 值可以减小插入损耗。
2-9 已知收音机某中放的负载回路如题2-4所示,回路的f 0=465kHz ,电感的Q 0=100,要求回路的带宽B=20kHz ,试求:(1)电感L 值;(2)回路插入损耗;(3)回路并联电阻R 1。
左侧电路的接入系数: 25.040120401=+=TT Tp 右侧电路的接入系数: 25.040120402=+=TT Tp 等效电源:ss i p i 1'=等效容抗: pFC 200=因为 LCf π210=mH Cf L 59.041202==πi 题图2-4·20·回路Q 值:25.230==Bf Q L插入损耗: 70.11120=⎪⎪⎪⎪⎭⎫ ⎝⎛-=Q Q K L l 回路并联电阻:Ω===K LQ f LQ R L L p p 4020πω Ω=Ω==K K p R R s s 32025.020221'Ω=Ω==K K p R R s L 3225.02221'因为 1''////R R R R L s p = Rp>RL?2-10 给定一频率可变的信号源及高频电压表,能否测出一未知电感线圈的L 及Q 值,试画出测试原理图并作简单说明。
按照图1连接电路调节信号源频率,当幅值为,频率为时,电压表读数为1I 1ω1U 调节信号源频率,当幅值为,频率为时,电压表读数为2I 2ω2U ⎪⎩⎪⎨⎧=+=+∙∙22221111U I R LI j U I R LI j eq eq ωω⎪⎩⎪⎨⎧=+=+222222122211U R L I UR L I eq eq ωω 由以上方程可解得和,L eq ReqR LQ ω=2-11 有一并联回路的某频段内工作,频段最低频率为535kHz ,最高频率为1605kHz 。
现有两个可变电容器,一个电容的最小电容量为12pF ,最大电容量为100pF ;另一个电容器的最小电容量为15pF ,最大电容量为450pF 。
试问:(1)应采用哪一个可变电容器,为什么?(2)回路电感应等于多少?(3)绘出实际的并联回路图。
s i·21·2-12 给定串联谐振回路的f 0=1.5MHz, C 0=100pF, 谐振时电阻R =5Ω。
试求Q 0和L 0。
又若信号源电压振幅V s =1mV ,求谐振时回路中的电流I 0以及回路元件上的电压V L0和V c0。
, 00021C L f π=mH L 113.00=21320000==R L f Q π当回路谐振时,,mA mVR V I s 2.0510=Ω==mVI L j V V C L 21300000===ω2-13 给定题图2-5并联谐振回路的f 0=5MHz ,C =50Pf ,通频带2∆f 0.7=150kHz 。
试求电感L 、品质因数Q 0以及对信号源频率为5.5MHz 时的失调。
又若把2∆f 0.7加宽到300kHz ,应在回践两端再并联上一个阻值多大的电阻。
R LI 题图2-5因为因为 LC f π210=所以 H C f L μππ26.201050)105(414112262202=⨯⨯⨯⨯⨯==-回路Q 值:3.330==BfQ L 频率为5.5MHz 时的失调为:05.65.55.023.332=⨯⨯=∆⋅=p L Q ωωξQ0=?2-14 如图2-6所示。
已知L =0.8μH ,Q 0=100,C 1=C 2=20P ,Ci=5pF ,R i =10k Ω,C 0=2Pf ,R 0=5k Ω。
试计算回路谐振频率、谐振阻抗(不计R 0与R i 时)、有载Q L 值和通频带。
s h e·22·o题图2-6pFCCC22'2=+=所以接入系数21222022''1=+=+=CCCp把R0折合到回路两端,得Ω=⨯==kpRR25.11495'2又pFCCCCCCi3.18222022205''11=+⨯+=++=∑谐振频率为MHzLCfp6.41103.18108.021221126=⨯⨯⨯==--∑ππ谐振阻抗为Ω=⨯⨯⨯⨯⨯==-kLQRpp9.20108.0106.41210066πω总电导为SRRRgpi6333107.236109.2011025.111101011'11-∑⨯=⨯+⨯+⨯=++=因而Ω==∑∑kgR2.41最后得2.20108.0106.412107.23611666=⨯⨯⨯⨯⨯⨯==--∑πωLgQpLMHzQffLp06.227.0==∆2-15 为什么耦合回路在耦合大到一定程度时,谐振曲线出现双峰?·23·因为,42222max22)1(2)1(2ξξηηηα+-++==I I 当>1时,第二项变负值。
η22)1(2ξη-随着的增大,此负值也随着增大,所以分母先是减小,当较大时,分母中的ξξ第三项的作用比较显著,分母有随的增大而增大。
因此,随着的增大,值4ξξξα先是增大,而后有减小。
这样,频率特性在的两边就必然出现双峰,在处0=ξ0=ξ为谷点。
2-16 假设有一中频放大器等效电路如题图2-7所示。
试回答下列问题:1)如果将次级线圈短路,这时反射到初级的阻抗等于什么?初级等效电路(并联型)应该怎么画?2)如果次级线圈开路,这时反射阻抗等于什么?初级等效电路应该怎么画?3)如果ωL 2=,反射到初级的阻抗等于什么?21C ω1) 如果将次级线圈短路,次级线圈的自阻抗为211L j Z ω= 反射阻抗 2222112)()(L M j L j M Z M R f ωωωω-===2) 如果次级线圈开路, ∞=11Z 反射阻抗 0)(2=∞=M R f ω3)如果ωL 2=, 21C ω2111G Z =反射阻抗 2222)(G M Z M R f ωω==IG 2题图2-72-17有一耦合回路如题图2-8所示。
已知n n he ·24·f 01=f 02=1MHz ;ρ1=ρ2=1k Ω;R 1=R 2=20Ω,η=1。
试求:1)回路参数L 1、L 2,C 1,C 2和M ;2)图中a 、b 两端的等效谐振阻抗Zp ;3)初级回路的等效品质因数Q 1;4)回路的通频带B ;5)如果调节C 2使f 02=950kHz (信号源频率为1MHz )。
求反射到初级回路的串联阻抗。
它呈感性还是容性?题图2-81)因f 01=f 02,R 1=R 2,,所以两回路参数相同,即L 1=L 2,C 1=C 2。
21ρρ=由 L 0ωρ=得 H L L L μπωρ159********021=⨯====pF LC C C 159101591041161222021=⨯⨯⨯====-πω根据获得最佳全谐振的条件:1221)(R R M R f ==ω212)(R R M =ω得HR R M μπω18.3202010211621=⨯==2)在全谐振条件下,Zp 为纯阻性,Ω==+==k R R R Z f p p 2540)1000(2112ρ3)初级等效回路品质因数为,2520210002111=⨯==R Q ρ·25·4)50201000'111===R Q ρ通频带为:kHzQ f f 3.2850102'226107.0=⨯=⨯=∆5)当f 02=950kHz 时,信号源频率仍为1MHz ,此时次级回路对信号源频率呈现感性,因而反射到初级回路的串联阻抗应呈容性。