光谱线增宽

谱线宽度和波长的关系
光谱线是指星体或某种自然物质在其特定工作环境下，在光谱面上产生的一些
明暗线，是对对象特定光谱状态的图形描述，又称光谱条纹。

一般而言，光谱线的宽度与其所处的环境有关。

研究表明，光谱线宽度受到物
质温度、压力和光源强度等多种因素的影响，这些因素都会影响光谱线的宽度。

温度是影响光谱线宽度的最重要因素之一。

特别是在较低温度的情况下，光谱
线的宽度变得越来越窄，当温度上升时，光谱线宽度也会不断增加，但最终会稳定在一个宽度值。

压力也会影响光谱线宽度。

低压往往会加宽光谱线，而高压可以使其变窄，但
影响并不明显，因此这种影响被认为是相对较小的。

同样，光源强度也会影响光谱线宽度，当光源强度增强时，光谱线的宽度就会
变窄，而弱光源就会使光谱线加宽，但这种影响也不是很显著，因此往往被忽略。

此外，波长也会影响光谱线的宽度。

一般而言，根据Kirchhoff定律，波长越短，光谱线宽度越窄，原因是较短的波长更容易发射和激发出特定的光谱线。

另外，也存在一些受激离子态寿命影响的特殊波长，这些波长的光谱线宽度要远大于相应温度下的标准宽度。

总之，光谱线宽度与波长的关系是受因温度、压力、光源强度以及特定离子态
寿命等多种因素影响的，且影响程度不同，需要仔细研究才能得出结论。

光谱线增宽matlab光谱线增宽是指当光通过一个物质或系统时，光谱线的宽度发生变化。

光谱线增宽的原因有很多，包括多种多样的自然和人为因素。

在这篇文章中，我们将使用MATLAB来介绍关于光谱线增宽的一些基本概念和方法。

在MATLAB中，我们可以使用“broaden.m”函数来模拟光谱线的增宽。

首先，我们需要安装并导入MATLAB的信号处理工具箱，该工具箱包含了许多用于信号处理和频谱分析的函数。

要使用MATLAB的信号处理工具箱，可以使用下面的代码导入：matlabpkg load signal接下来，我们将定义一个函数来模拟光谱线增宽。

我们可以使用高斯函数来描述具有固定中心频率和宽度的光谱线。

高斯函数可以表示为：matlabfunction y = broaden(x, sigma)y = exp(-x.^2 / (2 * sigma.^2));end其中，x是表示频率的数组，sigma是高斯函数的标准差，用于控制光谱线的宽度。

函数内的指数部分使用MATLAB的.运算符表示对数组的每个元素进行操作。

现在，我们可以使用该函数来生成一个具有特定参数的光谱线。

例如，下面的代码生成一个具有中心频率为0和宽度为0.1的光谱线：matlabx = -10:0.01:10;y = broaden(x, 0.1);plot(x, y);在这段代码中，我们定义了一个频率范围从-10到10的数组x，使用0.01的步长。

然后，我们使用broaden函数生成一个具有中心频率为0和宽度为0.1的光谱线，并将其绘制出来。

现在，让我们考虑光谱线增宽的几种常见原因。

首先，光谱线的增宽可能是由于仪器或测量系统的限制引起的。

例如，仪器的分辨率有限，无法准确测量非常窄的光谱线。

此外，仪器的噪声、漂移和非线性特性也可能导致光谱线增宽。

在MATLAB中可以使用以下代码来模拟仪器限制引起的光谱线增宽：matlabx = -10:0.01:10;y = broaden(x, 0.1); 原始光谱线noise = rand(size(x)); 产生一个与x大小相同的随机噪声数组y_noisy = y + noise; 添加噪声plot(x, y_noisy);在这个例子中，我们通过添加一个与x大小相同的随机噪声数组来模拟仪器噪声。

多普勒加宽公式一、引言多普勒加宽公式是多普勒效应在光谱学中的一个重要应用，它描述了由于分子或原子相对于观测者的运动速度而引起的光谱线加宽的现象。

多普勒加宽是由于光波在传播过程中受到分子或原子的散射作用，而散射作用的频移取决于光源与散射物质之间的相对运动。

因此，多普勒加宽公式的理解与运用对于光谱分析和物理现象的深入探讨具有重要意义。

二、多普勒加宽公式的原理多普勒加宽公式的理论基础是多普勒效应。

当光源相对于观测者运动时，观测者接收到的光的频率会发生变化。

当光源向观测者运动时，观测者接收到的光的频率会增大；而当光源远离观测者运动时，观测者接收到的光的频率会减小。

这种由于光源与观测者之间的相对运动而引起的光谱线位移的现象称为多普勒效应。

在多普勒加宽公式中，光谱线的宽度与散射物质的热运动速度有关。

由于分子或原子的无规则热运动，光波在传播过程中会不断地与散射物质发生相互作用，从而引起光谱线的加宽。

这种加宽现象称为多普勒加宽。

三、多普勒加宽公式的数学表达多普勒加宽公式的数学表达为：ΔvD = 1/λ，其中ΔvD是多普勒加宽引起的频移量，λ是光源的波长。

这个公式表明，多普勒加宽与光源波长的倒数成正比。

因此，对于较长的波长，多普勒加宽的影响更大。

这也是为什么在红外光谱和微波谱中，多普勒加宽是一个需要考虑的重要因素。

四、多普勒加宽的应用多普勒加宽在许多领域都有广泛的应用，尤其在气体检测、激光光谱学和遥感等领域中具有重要的作用。

在气体检测中，由于不同气体的多普勒加宽不同，通过对光谱线的宽度进行分析，可以实现对气体的定性和定量分析。

在激光光谱学中，由于激光具有较高的频率和波长，多普勒加宽对激光光谱的影响较大，通过对多普勒加宽的研究，可以提高光谱分析的精度和准确性。

此外，在遥感领域中，通过研究地球大气中气体分子的多普勒加宽，可以实现对地球大气的遥感监测。

五、结论多普勒加宽公式是多普勒效应在光谱学中的重要应用，它描述了由于分子或原子相对于观测者的运动速度而引起的光谱线加宽的现象。

光谱线的碰撞展宽和多普勒展宽的产生
光谱线的碰撞展宽是指由于原子或分子与其他粒子的碰撞而导致的线宽增加。

当光通过原子或分子气体时，会和气体中的原子或分子发生碰撞。

碰撞会导致原子或分子的能级发生变化，从而使得光谱线的频率发生变化。

碰撞引起的能级变化会导致光谱线的展宽增加，即波长范围增大。

多普勒展宽是指由于源或接收者的运动而导致的光谱线的展宽。

当光源或接收者相对于观测者运动时，光谱线的频率会相对于静止时产生变化。

这是由于多普勒效应的影响引起的。

多普勒效应是指当发光源与观察者之间存在相对运动时，观察者所观测到的光谱线频率会发生变化。

源或接收者向观察者靠近时，光谱线的频率会增加，即波长变短，导致光谱线展宽增加。

总而言之，光谱线的碰撞展宽是由于碰撞引起的能级变化而导致的，光谱线的多普勒展宽是由于源或接收者的运动而引起的。

这两种展宽机制都会使得光谱线的展宽增加，波长范围变大。

1. 均匀增宽介质的增益系数与反转粒子数的饱和效应(1). 均匀增宽型介质的增益系数通常来说，增益系数的表达式有最常见的两种表述方式：1）从光在介质中传播规律的表达式出发：221211()(0)exp[()()]g I z I n n B f h z g cμνν=- 21()G nB f h c μνν=∆2）从增益系数的物理含义出发：()()dI z G I z dz=⋅ 物理意义：光波在介质中传播单位距离后，光强的增加量占总光强的百分比，也代表了介质对光放大能力的大小。

dI G I dz =⋅1v d h h dt ϕνϕν=⋅1v d dtϕϕ=⋅ 由于大部分激光工作物质都是四能级系统，所以我们从四能级速率方程出发，来进一步推导增益系数的表达式：在不计损耗时，工作物质中光子数密度的速率方程为：221112d n W nW dtϕ=- 221112v v n n σϕσϕ=-21v n σϕ=∆dI G I dz =⋅1v d dtϕϕ=⋅21n σ=∆ 21()G nB f h c μνν=∆ 光在介质中传播规律21G n σ=∆ 四能级速率方程2212120v ()8A f σνπν=+3 3.213218A h B c πνμ= 21()G nB f h c μνν=∆ 光在介质中传播规律21G n σ=∆ 四能级速率方程从上述两式中不难发现，无论哪种表达方式，增益系数都正比于反转粒子数密度.因此进一步讨论反转粒子数密度不同情况下的表达式及其饱和效应也就十分必要了(2). 反转粒子数的饱和效应在激光器连续运转工作状态时，各能级粒子数密度会达到稳定的动态平衡，我们在上一讲中曾推导出四能级系统中稳定状态下粒子数密度反转的表达2121v n n στϕ∆∆=+ v I h ϕν=()()212()n=11v v s n n I I h I νστν∆∆∆=++ 212()s h I ννστ=饱和光强()s I ν的物理意义是：当入射光强度()v I 可以和饱和光强()s I ν相比拟时，受激辐射造成的上能级反转粒子数的衰减率才可以与其他弛豫过程（自发辐射和无辐射）相比拟，因此：当()v I <<()s I ν时，反转粒子数密度与光强无关；当()v I 与()s I ν可相比拟时，反转粒子数密度随光强的增加而减少；当()v I =()s I ν时，反转粒子数密度下降了一半密度称为大信号反转粒子数密度。

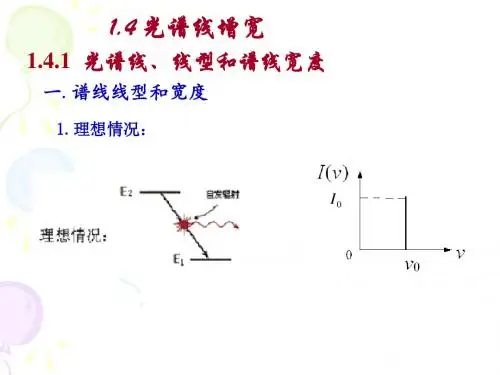
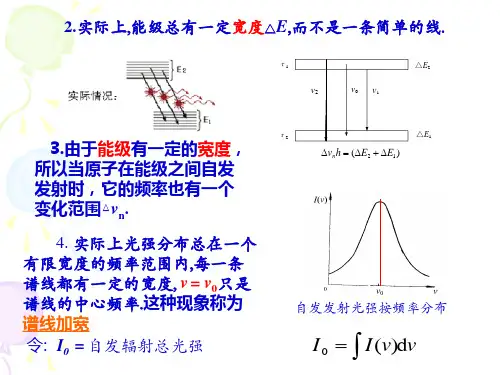
2.2谱线的增宽光谱的线型和宽度与光的时间相干性直接相关，对后面要讲的激光的增益、模式、功率等许多激光器的输出特性都有影响，所以光谱线的线型和宽度在激光的实际应用中是很重要的问题。

2.2.1光谱线、线型和光谱线宽度由于原子发光是有限波列的单频光，因而仍然有一定的频率宽度。

实际上使用分辨率很高的摄谱仪来拍摄原子的发光光谱，所得的每一条光谱线正是这样具有有限宽度的。

这意味着原子发射的不是正好为某一频率0ν(满足021h E E ν=-)的光，而是发射频率在0ν附近某个范围内的光。

实验还表明，不仅各条谱线的宽度不相同，就每一条光谱线而言，在有限宽度的频率范围内，光强的相对强度也不一样。

设某一条光谱线的总光强为0I ，测得在频率ν附近单位频率间隔的光强为()I ν，则在频率ν附近，单位频率间隔的相对光强为0()I I ν，用()f ν表示，即0()()I f I νν=(2-8)实验测得，不同频率ν处，()f ν不同，它是频率ν的函数。

如以频率为横坐标、()f ν为纵坐标，画出()f νν-曲线如图2-3(a)所示。

()f ν表示某一谱线在单位频率间隔的相对光强分布，称做光谱线的线型函数，它可由实验测得。

图2-3光谱的线型函数(a)实际线型(b)理想线型为便于比较，图2-3(b)画出了理想情况的单色光的相对光强分布。

对比(a)、(b)两图，明显看出，理想的单色光只有一种频率，且在该频率处的相对光强为1，即光强百分之百集中在此频率。

这种情况实际上是不存在的，实际情况如图2-5(a)，光强分布在一个有限宽度的频率范围内。

相对光强在0ν处最大，两边逐渐减小，0ν是谱线的中心频率。

现在讨论频率为ν到ν+d ν的频率间隔范围内的光强，它应该是在ν附近单位频率间隔内的光强()I ν乘以频率宽度d ν，即为()I d νν，同时，它也应等于光谱线总光强0I 与频率ν附近d ν范围的相对光强()f d νν的乘积。

所以0()()I d I f d νννν=(2-8)图2-5(a)中曲线下阴影面积为0()()I d f d I νννν=，表示频率在ν－ν+d ν范围的光强占总光强的百分比。