第七章时间数列练习题教学文案
- 格式:doc
- 大小:89.00 KB
- 文档页数:11


第七章时间数列分析一、填空题1、时间指标数值2、逐期增长量累计增长量3、增长水平(或增长量)发展速度4、本期水平去年同期水平5、年距发展速度 1(或100%)6、几何平均法方程法7、同季(月)平均法趋势与季节模型法8、平均季节比重法平均季节比率法9、报告期水平基期水平10、序时平均数(或动态平均数)平均数11、和差12、季节变动长期趋势13、逐期增长量环比增长速度14、长明显1-5 A C C A D 6-10 A B A D B三、多选题1、CDE2、ABDE3、ABCE4、ACDE5、BDE6、BD7、ABCD8、ACE9、AE 10、ACE四、简答题1、序时平均数与一般平均数的异同。
答:(1)相同之处。
二者都是将具体数值抽象化,用一个代表性的数指来代表总体的一般水平。
(2)不同之处。
①计算的依据不同。
一般平均数是根据变量数列计算的,而序时平均数则是根据时间数列计算的;②对比的指标不同。
一般平均数是总体标志总量与总体单位总量对比的结果,而序时平均数则是时间数列各期发展水平的总和与时期项数对比的结果;③说明的问题不同。
一般平均数说明现象在同一时间、不同空间上所达到的一般水平,而序时平均数则说明现象在同一空间、不同时间上所达到的一般水平。
2、时期数列与时点数列的区别。
答:①时期数列中的指标值为时期数,时点数列中的指标值为时点数;②时期数列中的指标值具有可加性,而时点数列中的指标值则不具有可加性;③时期数列中指标值的大小与时间间隔的长短有直接关系,而时点数列中指标值的大小与时间间隔的长短则没有直接关系;④时期数列中的指标值是通过连续调查取得的,而时点数列中的指标值则是通过一次性调查取得的。
3、时间数列的编制原则。
答:(1)基本原则:保持数列中的各项指标数值具有可比性。
(2)具体原则:①时间长短统一;②总体范围统一;③指标口径统一;④计算方法统一;⑤计量单位统一。
4、计算和应用平均速度应注意的问题。

五年、月、日6练习七●教学内容苏教版义务教育教科书《数学》三年级下册第56~57页的练习七第1~7题和“思考题”。
●教学目标1.结合具体的生活情境巩固24时记时法,会用24时记时法正确表示一天中的某个时刻,能正确进行普通记时法与24时记时法之间的相互转换。
2.联系生活经验,掌握求简单经过时间的方法,能正确解答一些相关的实际问题,进一步发展推理能力。
3.在学习过程中,进一步体会数学思考的严谨性,感受数学与生活的联系,培养对数学的积极情感,体会合理安排时间的重要性,养成珍惜时间的良好习惯。
●教学重点熟练将24时记时法与普通记时法相互转换,计算简单的经过时间。
●教学难点进一步巩固简单的经过时间计算。
●教学准备多媒体课件、学习单。
▍流程一:激趣导入,唤起旧知1.出示情境:小芳和爸爸、妈妈准备利用暑假外出旅游,计划8月5日从南京乘火车去北京,8月9号从北京乘飞机返回。
下面是小芳收集的部分信息:(1)从表中你知道了哪些信息你从表中读到哪些关于时间的信息说给同桌听一听。
(2)如果让你给些建议,你会如何选择 预设:出发及到达的时刻因素:将出发时间和到达时间的24时记时法转换为12时记时法,结合实际想一想是否合适。
旅途耗时因素:计算经过时间,时间短的更合适。
价格因素:参考票价选择班次。
(3)这几班列车或火车都是几点出发,几点到达,你能用12时记时法说给同桌听一听吗(4)坐火车最快多长时间到达,比其他的列车快了多少飞机呢独立思考,在学习单上算一算,在小组里说说你的想法。
●教学过程(1)请拿出学习单,自己边回忆、边梳理,再在小组里交流各自的想法。
学生反馈整理的情况,教师点评。
(2)对比几位同学的作品,你更喜欢哪种整理的方式你最欣赏谁的作品,他好在哪里(3)相关的两个知识点还有哪些值得强调和注意的地方▍流程二:自主探究,巩固知识1.做练习七第1题以下这几个时刻,你能进行互相转换吗连连线。
12:00 21:00 7:00 19:00 15:00早上7时下午7时中午12时下午3时晚上9时(1)独立完成。
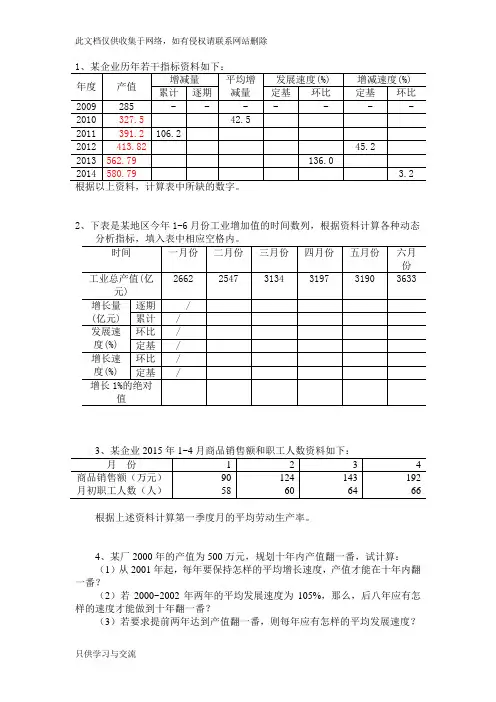
2、下表是某地区今年1-6月份工业增加值的时间数列,根据资料计算各种动态根据上述资料计算第一季度月的平均劳动生产率。
4、某厂2000年的产值为500万元,规划十年内产值翻一番,试计算:(1)从2001年起,每年要保持怎样的平均增长速度,产值才能在十年内翻一番?(2)若2000~2002年两年的平均发展速度为105%,那么,后八年应有怎样的速度才能做到十年翻一番?(3)若要求提前两年达到产值翻一番,则每年应有怎样的平均发展速度?5.2008年末我国人口为13.28亿人,为争取2020年末我国人口控制在15亿以内,要求(1)计算年人口平均增长率(2)若从2009年起人口年平均增长率控制在1%之内,试计算2020年末我国人口数。
年份2010 2011 2012 2013 2014 水稻产量(万吨)320 332 340 356 3807.2004~2008年广东省国内生产总值环比增长速度依次为:14.8%、13.8%、14.6%、14.7%、12.7%,试计算广东省这几年国内生产总值的平均增长速度。
若按照此速度发展,广东省需要多少时间可以实现国内生产总值翻两番?9.某银行2015年第二季度存款余额如下,求第二季度各月平均存款余额月份3月末4月末5月末6月末存款余额2500 2690 3000 4000(万元)10.某班级10月份到校人数如下,求10月份平均到校人数时间1日4日10日16日21日28日31日人数50 55 53 54 50 52 51 11.某建筑工地工人数12月份增减变动如下,1日工人总数500人,18日15人离开工地,24日35人离开工地。
试分别计算12月该工地的平均人数。
12.某工厂历年产量资料如下:年份2005 2006 2007 2008 2009 2010 2011 产量(万件)16 24 28 32 38 42 4813.我国2002年总人口为128453万人,2011年总人口为134735万人,试计算在这期间我国人口平均增长率为多少?若按照这个速度发展,则2020年末我国人口将达到多少?14.某企业生产的产品产值资料如下试计算:(1)应用三项移动平均法计算趋势值。


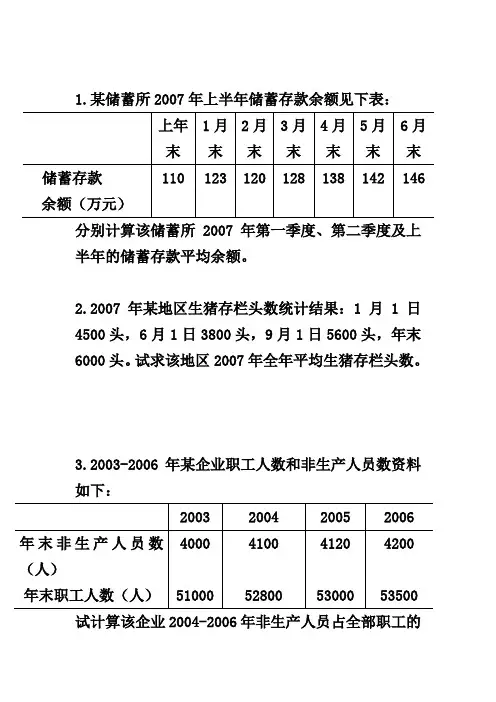
1.某储蓄所2007年上半年储蓄存款余额见下表:分别计算该储蓄所2007年第一季度、第二季度及上半年的储蓄存款平均余额。
2.2007年某地区生猪存栏头数统计结果:1月1日4500头,6月1日3800头,9月1日5600头,年末6000头。
试求该地区2007年全年平均生猪存栏头数。
3.2003-2006年某企业职工人数和非生产人员数资料如下:试计算该企业2004-2006年非生产人员占全部职工的平均比重。
4.某企业6-9月产值及职工人数资料如下:(1)求该企业第三季度各月平均全员劳动生产率;(2)求该企业第三季度全员劳动生产率。
5.某地区某年的人口资料如下:单位:万人求:(1)该地区该年第三季度平均人口数;(2)该地区该年下半年平均人口数。
年产品产量资料如下6.某企业2001—2006(2)计算该企业2001年至2006年这五年期间的产品产量的年平均增长量以及按水平法计算的年平均增长速度。
7、填表8.某企业单位成本1998比1997年降低2%,1999比1998年降低5%,2000比1999年降低3%,2001比2000年降低1.5%,计算1998-2001年该企业单位成本总的降低速度和平均降低速度。
10、某公司两个企业2002年2月份产值及每日个人在册资料:11、已知2000年我国国民收入生产额为14300亿元,若以平均每年增长5%的速度发展,到2010国民收入生产额达到什么水平?12、某地区1985年国民收入12亿元,如果以后平均每年递增8.1%,多少年后该地区国民收入可达60亿元。
13、某工厂产值1998比1997年增长7%,1999比1998年增长10.5%,2000比1999年增长7.8%,2001比2000年增长14.6%,,计算1998-2001年总产值的增长速度和平均增长速度。
14、某地区1990年底人口数为2000万人,假定以后每年以9‰的增长率增长;又假定该地区1990年粮食产量为120亿斤,要求到1995年平均每人粮食达到800斤,计算1995年的粮食产量应该达到多少斤?粮食产量每年的平均增长速度如何?15、某公司1989年销售额为1800万元,若1990-1993年销售额每年平均增长8%,1994-1997年销售额每年平均增长12%,1998-2000年销售额平均每年增长15%。

统计学原理第七章 时间数列计算题 例7-1:某工业企业资料如下:要求计算:(1)一季度月平均工业增加值;(2)一季度月平均工人数; (3)一季度月平均劳动生产率; (4)一季度劳动生产率。
例7-2:某企业2003年有关某一产品的生产资料如下:要求:(1)用水平法计算该产品产量在第二季度的月平均增长速度;(2)计算生产工人人数在第二季度的月平均增长量; (3)计算第二季度的月平均劳动生产率。
(1)产量的平均发展速度%65.101296310330===a a x n(2)三月份工人人数25122502521=+=b (人) 六月份工人人数24922562423=+=b (人) 第二季度工人数的月平均增长量13251249303-=-=-=b b d (人)(3)30633103083003321=++=++=a a a a (件) 321214321b b b b b +++=67.25132562124226025021=⨯+++⨯=(人)b ac =22.167.251306==(件/人)例7-3:已知下列资料计算:(1)第二季度每月劳动生产率;(2)第二季度平均月劳动生产率; (3)二季度劳动生产率。
例7-4:某商店有关资料如下:试计算:(1)各月商品周转次数(2)第一季度平均每月的商品周转次数 (3)第一季度商品周转次数(1)一月份商品周转次数=)(22100次= 二月份商品周转次数=)(325452159次=+三月份商品周转次数=)(5.225054130次=+(2))(51.23/1553/3893/)2505452248(3/)130159100(次==+++++==b ac (3))(53.751.23次=⨯=⋅c n例7-5:某彩电仓库4月1日有300台彩电,4月3日调出150台,4月6日调进200台,4月15日调出100台,4月22日调出120台,4月26日调进142台。
试求该仓库4月份的平均库存量。

时间序列练习题时间序列分析是一种对随时间变化的数据进行建模和预测的统计分析方法。
它在经济学、金融学、气象学、环境科学等领域都有着广泛的应用。
为了加深对时间序列分析的理解,以下是一些时间序列练习题,帮助读者巩固相关知识和技能。
1. 下面是某城市某共享单车平台的日订单量数据(单位:订单数)。
请问这组数据属于哪种类型的时间序列数据?日期订单量1月1日 1201月2日 1601月3日 1501月4日 1801月5日 2002. 下面是某公司某产品在2020年1月至6月的月销售额数据(单位:万元)。
请根据给出数据回答以下问题:1月 802月 853月 704月 905月 956月 100(1)请计算该产品在第二季度(4月、5月、6月)的总销售额。
(2)根据给出数据,绘制该产品的销售额趋势图。
3. 下面是某超市某商品每周销量数据(单位:件)。
请计算该商品的季节性指数。
周次销量1 1002 1203 1354 1405 1506 1557 1608 1809 20010 2204. 假设一家公司的销售额数据如下(单位:万元):日期销售额2019-01 802019-02 852019-03 902019-04 1002019-05 1102019-06 115(1)请计算该公司在2019年第一季度(1月、2月、3月)的平均月销售额。
(2)根据给出数据,绘制该公司的销售额线性趋势图。
5. 下面是某餐厅某菜品2019年1月至6月的月销售量数据(单位:份)。
请根据给出数据,计算该菜品的季节指标和趋势指数。
1月 502月 553月 484月 605月 656月 70以上是时间序列练习题,通过思考和计算这些问题,读者可以进一步巩固和应用时间序列分析的相关知识和方法。
在实际应用中,时间序列分析可以用于预测未来趋势、制定合理的经营策略、评估政策实施效果等。
希望读者通过练习题的探索,能够更好地理解时间序列分析的重要性和实用性。

求数列的通项公式(教案+例题+习题)一、教学目标1. 理解数列的概念,掌握数列的基本性质。
2. 学会求解数列的通项公式,并能应用于实际问题。
3. 培养学生的逻辑思维能力和运算能力。
二、教学内容1. 数列的概念与基本性质2. 数列的通项公式的求法3. 数列通项公式的应用三、教学重点与难点1. 教学重点:数列的概念,数列的通项公式的求法及应用。
2. 教学难点:数列通项公式的推导和应用。
四、教学方法1. 采用讲授法,讲解数列的概念、性质及通项公式的求法。
2. 利用例题,演示数列通项公式的应用过程。
3. 布置习题,巩固所学知识。
五、教学过程1. 引入数列的概念,讲解数列的基本性质。
2. 讲解数列通项公式的求法,引导学生掌握求解方法。
3. 通过例题,演示数列通项公式的应用,让学生理解并掌握公式。
4. 布置习题,让学生巩固所学知识,并提供解题思路和指导。
5. 总结本节课的重点内容,布置课后作业。
教案结束。
例题:已知数列的前n项和为Sn = n(n+1)/2,求该数列的通项公式。
解答:由数列的前n项和公式可知,第n项的值为Sn S(n-1)。
将Sn = n(n+1)/2代入上式,得到第n项的值为:an = Sn S(n-1) = n(n+1)/2 (n-1)n/2 = n/2 + 1/2。
该数列的通项公式为an = n/2 + 1/2。
习题:1. 已知数列的前n项和为Sn = n^2,求该数列的通项公式。
2. 已知数列的通项公式为an = 2n + 1,求该数列的前n项和。
3. 已知数列的通项公式为an = (-1)^n,求该数列的前n项和。
4. 已知数列的通项公式为an = n^3 6n,求该数列的前n项和。
5. 已知数列的通项公式为an = 3n 2,求该数列的前n项和。
六、教学目标1. 掌握数列的递推关系式,并能运用其求解数列的通项公式。
2. 学习利用函数的方法求解数列的通项公式。
3. 提升学生分析问题、解决问题的能力。

《时间序列》练习题及解答一、单项选择题从以下各题所给的 4 个备选答案中选出 1 个正确答案,并将其编号( A、B、C、D)填入题干后边的括号内。
1、组成时间数列的两个基本因素是()。
A、主词和宾词B、变量和次数C、时间和指标数值 D 、时间和次数2、最基本的时间数列是()。
A、时点数列B、绝对数数列 C 、相对数数列D、均匀数数列3、时间数列中,各项指标数值能够相加的是()。
A、相对数数列B、期间数列 C 、均匀数数列D、时点数列4、时间数列中的发展水平()。
A、只好是总量指标B、只好是相对指标C、只好是均匀指标D、上述三种指标均能够5、对时间数列进行动向剖析的基础指标是()。
A、发展水平B、均匀发展水平C、发展速度D、均匀发展速度6、由中断时点数列计算序时均匀数,其假设条件是研究现象在相邻两个时点之间的变动为()。
A、连续的B、中断的C、稳固的 D 、均匀的7、序时均匀数与一般均匀数的共同点是()。
A、二者均是反应同一整体的一般水平B、都是反应现象的一般水平C、二者均可除去现象颠簸的影响D、共同反应同质整体在不一样时间上的一般水平8、时间序列最基本的速度指标是()。
A、发展速度B、均匀发展速度C、增添速度D、均匀增添速度9、依据采纳的对照基期不一样,发展速度有()。
A、环比发展速度与定基发展速度B、环比发展速度与积累发展速度C、逐期发展速度与积累发展速度D、积累发展速度与定基发展速度10、假如时间序列逐期增添量大概相等,则宜配合()。
A、直线模型 B 、抛物线模型 C 、曲线模型 D 、指数曲线模型11、某商场第二季度商品零售额资料以下:月份 4 月 5 月 6 月达成商品零售额(万元)506278达成计划( %)100124104该商场第二季度均匀达成计划为()。
A、 100%124%104%108.6%3B、506278108.6% 506278100%124%104%50 62 78C 、 100% 124% 104% 92.1%50 62 78D 、50100% 62 124% 78 104%109.5%50 62 7812、增添速度的计算公式为( )。
数列综合题和应用性问题教案一、教学目标1. 让学生掌握数列的基本概念和性质,包括等差数列、等比数列等。
2. 培养学生解决数列综合题的能力,提高逻辑思维和运算能力。
3. 培养学生将数列知识应用于实际问题的能力,提高解决问题的综合素质。
二、教学内容1. 等差数列的性质及求和公式2. 等比数列的性质及求和公式3. 数列的通项公式及其应用4. 数列的极限概念及数列极限的计算5. 数列综合题的解题策略三、教学重点与难点1. 重点:等差数列和等比数列的性质、求和公式,数列极限的计算。
2. 难点:数列综合题的解题方法,数列知识在实际问题中的应用。
四、教学方法1. 采用案例教学法,以典型例题引导学生掌握数列知识。
2. 运用问题驱动法,激发学生思考,培养学生解决实际问题的能力。
3. 利用数列软件工具,直观展示数列的变化规律,增强学生的直观感受。
4. 组织小组讨论,引导学生相互交流,提高团队合作能力。
五、教学安排1. 第一课时:等差数列的性质及求和公式2. 第二课时:等比数列的性质及求和公式3. 第三课时:数列的通项公式及其应用4. 第四课时:数列的极限概念及数列极限的计算5. 第五课时:数列综合题的解题策略及应用教案内容依次展开,包括每个章节的具体教学目标、教学内容、教学步骤、课堂练习、课后作业等。
请根据实际教学需求进行调整和完善。
六、教学目标1. 让学生掌握数列的通项公式的推导和应用,能够利用通项公式解决实际问题。
2. 培养学生解决数列极限问题的能力,理解数列极限的概念和计算方法。
3. 培养学生运用数列知识分析和解决实际问题的能力,提高解决问题的综合素质。
七、教学内容1. 数列的通项公式的推导和应用2. 数列极限的概念和计算方法3. 数列极限在实际问题中的应用4. 数列综合题的解题策略5. 数列知识在实际问题中的应用案例分析八、教学重点与难点1. 重点:数列通项公式的推导和应用,数列极限的计算方法。
2. 难点:数列极限的理解和应用,数列综合题的解题策略。
(时间管理)练习时间数列分析第七章时间数列分析壹、填空题1. 1.时间数列是指,它包含和俩个要素。
2. 2.编制时间数列基本原则是。
3. 3.以时间数列为基础的动态分析包括和俩个基本分析内容。
4. 4.影响时间数列中某壹指标各个数值的因素有, , 和.它们的共同影响能够用和俩个模型加以描述。
5. 5.时间数列的种类有,和.其中为基本的时间数列,而和是属于派生的时间数列。
6. 6.绝对数时间数列可分为和。
7.7.于时点数列中俩个指标值之间的时间距离称为。
8.8.于时间数列动态分析中,俩个有直接数量关系的速度指标是和。
它们的关系是。
9.9.平均发展水平又称,它是对所计算的平均数。
10.10.水平法又称,应用水平法计算平均发展速度时n 是个数.从本质上讲,用这种方法计算平均发展速度的其数值仅仅受和的影响。
11.11.若对以季度为单位的时间数列求季节比率,则壹年内季节比率之和等于。
12.12.最小平方法的数学依据是,这壹方法既适用于趋势的拟合,也适用于趋势的拟合。
二、判断题1. 1.时间数列中各个指标值是不能相加的。
2. 2.由时点数列计算序时平均数,其假定前提是:于间隔期间现象是均匀变动的。
3. 3.平均增长速度是环比增长速度的平均值,它是根据各个环比增长速度直接计算的。
4. 4.各期发展水平之和和最初水平之比,等于现象发展的总速度。
5. 5.环比增长速度的连乘积等于定基增长速度。
6. 6.由相对数平均数时间数列计算序时平均数可采用。
7.7.若原数列的指标数值出现周期性的变化,应以周期的变化的长度作为移动平均数的项数。
8.8.移动平均法于 n 为偶数时,壹般要移动二次才能对正某个时期的趋势值。
9.9.移动平均法中,n 越大则移动平均法的修匀作用越小。
10.10.2000 年年底全国高等学校于校人数属于时期数列。
11.11.某企业 2001 年年底商品库存 380 万元是壹个时点数列。
12.12.序时平均数中的“首尾折半法”适用于计算间隔相等的时点数列。
数学计算课广告文案
学渣变学霸的最佳捷径!快来参加我们的数学计算课,让你的计算能力一飞冲天!
无论你是初学者还是进阶者,我们的数学计算课程都能给你提供所需的知识和技巧。
课程内容包括基本运算、数列、方程与不等式等,使你能够快速准确地解决各种数学计算问题。
我们的课程特点如下:
1. 灵活的学习时间安排:无论是上班族还是学生党,无论你是白天还是晚上有时间,我们都能为你提供合适的上课时段。
2. 个性化教学:我们注重学生的实际情况和学习需求,为每个学生制定个性化的学习计划,让你更好地掌握数学计算技巧。
3. 丰富的练习资源:我们准备了大量的练习题和考试题,帮助学生在实践中不断巩固所学的知识,并提高解题速度和准确率。
4. 知识点精讲:我们的老师将重点讲解数学计算的关键知识点和难点,帮助学生迅速理解和掌握解题方法。
5. 高效的教学方式:我们采用互动式授课和实例分析的方式,加深学生对数学计算技巧的理解和运用能力。
6. 班级互动交流:我们鼓励学生之间互相交流和合作,提供学习小组和讨论区,让学习变得更加有趣和高效。
参加我们的数学计算课,你将享受到全方位的学习体验,从而快速提高你的数学计算水平。
不再被数学困扰,成为真正的数学高手!立即报名,开启数学计算之旅吧!。
数列规律题初中教案教学目标:1. 理解数列的概念,掌握数列的通项公式。
2. 培养学生观察、分析、归纳数列规律的能力。
3. 培养学生解决问题的能力,提高逻辑思维能力。
教学重点:1. 数列的概念及通项公式的理解。
2. 数列规律的观察和分析。
教学难点:1. 数列规律的归纳和总结。
2. 应用数列规律解决问题。
教学准备:1. 数列相关知识PPT。
2. 数列规律题目及解答。
教学过程:一、导入(5分钟)1. 引导学生回顾数列的概念,复习数列的通项公式。
2. 提问:同学们,你们能想到一些数列的例子吗?它们有什么特点?二、新课讲解(15分钟)1. 讲解数列的概念,数列的定义:一个按照一定顺序排列的一列数。
2. 讲解数列的通项公式:数列的第n项可以表示为an = a1 + (n-1)d,其中a1是首项,d 是公差。
3. 讲解数列规律的观察和分析方法:a. 观察数列的单调性:数列是递增还是递减?b. 观察数列的周期性:数列是否有规律地重复?c. 观察数列的奇偶性:数列中的项是奇数还是偶数?d. 观察数列的间隔:数列中相邻两项的间隔是否有规律?三、课堂练习(15分钟)1. 给出数列规律题目,让学生独立解答。
2. 引导学生分析数列的规律,归纳总结。
四、讲解答案及解析(15分钟)1. 讲解学生解答的题目,指出解题思路和注意事项。
2. 分析数列规律的归纳和总结方法。
五、课堂小结(5分钟)1. 回顾本节课所学内容,数列的概念、通项公式和数列规律的观察分析方法。
2. 强调数列规律在实际问题中的应用价值。
六、作业布置(5分钟)1. 布置数列规律题目,要求学生独立完成并总结规律。
2. 鼓励学生查阅相关资料,深入了解数列的性质和应用。
教学反思:本节课通过讲解数列的概念、通项公式和数列规律的观察分析方法,使学生掌握了数列的基本知识,培养了学生的观察、分析、归纳能力。
在课堂练习环节,学生独立解答题目,提高了解决问题的能力。
然而,部分学生对于数列规律的归纳和总结仍存在困难,需要在课后加强练习和辅导。
第五章时间数列(动态)分析一、填空题1、动态平均数所平均的是现象某一指标在_____________ 的不同取值,一般平均数(静态平均数)所平均的则是总体各单位在 ___________ 的不同取值。
2、计算平均发展速度的方法有和两种。
3、如果时间数列的每期增减量大体相等,则这种现象的发展是呈___________ 发展趋势,可以配合相应的方程来预测。
4、已知某产品1991年比1990年增长了6%, 1992年比1990年增长了9%,则1992 年比1991年增长了-5、某产品成本从1990年到1995年的平均发展速度为98.3%,则说明该产品成本每年递减=二、选择题单选题:1、假设某产品产量1990年是1985年的135%,那么1986年一1990年的平均发展速度为()(1)肪成(2) V133% (3)^3^0(4) V135%2、某时期历年出生的人口数是一个()(1)时期数列(2)时点数列(3)连续性的时点数列(4)间断性的时点数列3、在对社会经济现象进行动态分析中,把水平分析和速度分析能够结合起来的分析指标是()(1)平均发展速度(2)平均发展水平(3)年距增长量(4)增长1%的绝对值4、某企业生产某种产品1990年比1989年增长了8%, 1991年比1989年增长12%则1991年比1990年增长了()(1)12%4-8%-100% (2) 108% 4-112%-100%(3) 112% 4-108%-100% (4) 108%X112%-100%5、设对不同年份的产品成本配合的趋势直线方程为Yt=75-1.85t, b=-1.85表示()(1)时间每增长一个单位,产品成本平均增加1.85个单位(2)时间每增长一个单位,产品成本增加总额为1.85个单位(3)时间每增长一个单位,产品成本平均下降1.85个单位(4)产品成本每变动t各单位,平均需要1.85年的时间6、若时间数列为指数曲线,其资料的变动特点为()(1)定基发展速度大体相等(2)环比发展速度大体相等(3)逐级增长量大致相等(4)二级增长量大体相等多选题:1、下列时间数列中属于时期数列的有()(1)各年末人口数(2)各年新增人口数(3)各月商品库存数(4)各月商品销售额(5)各月储蓄存款余额2、定基增长速度等于()(1)累计增长绝对量除以基期发展水平(2)环比增长速度的连乘积(3)环比增长速度的连乘积减去100%(4)定基发展速度减去100%(5)逐期增长量除以基期水平3、统计常用的动态平均数有()(1)平均发展水平(2)平均增长量(3)增长1%的绝对值(4)环比发展速度(5)平均发展速度4、以下可直接用最小二乘法计算模型参数的有()(1)直线趋势模型(2)二次曲线模型(3)指数趋势模型(4)回归线性模型5、时间数列的构成因素有()(1)长期趋势(2)季节变动(3)循环变动(4)不规则变动二、简答题1、什么是总速度?如何计算?2、什么是年距增长速度?计算它有什么作用?3、季节变动的测定方法有哪些?各种方法的应用条件是什么?4、用数学模型法测定长期趋势的基本思想是什么?其步骤是什么?5、平均发展速度的两种计算方法各有什么特点?应用是应注意什么?四、计算题1、某邮局一月份的职工人数变动如下:1 月1 I I 1 月9 H 1 月20 I I2 月1 I I50人52人58人57人计算该局一月份的平均每天职工人数。
第七章时间数列练习题第七章时间数列练习题 一、单项选择题1、对于季度时间数列,如果数列中没有不规则变动,则不规则变动相对数应为( ) ① 1 ② 0 ③ 4 ④ 122、根据月度时间数列资料,各月季节比率之和应为( ) ① 1 ② 0 ③ 4 ④ 123、已知环比增长速度为8.12%、6.42%、5.91%、5.13%,则定基增长速度为( ) ① 8.12%×6.42%×5.91%×5.13% ② 8.12%×6.42%×5.91%×5.13%-100% ③ 1.0812×1.0642×1.0591×1.0513 ④ 1.0812×1.0642×1.0591×1.0513-100%4、用最小平方法拟合直线趋势方程t yˆ=a +b t ,若b 为负数,则该现象趋势为( ) ① 上升趋势 ② 下降趋势 ③ 水平趋势 ④ 不能确定5、某企业某年各月月末库存额资料如下(单位:万元)4.8,4.4,3.6,3.2,3.0,4.0,3.6,3.4,4.2,4.6,5.0,5.6;又知上年末库存额为5.2。
则全年平均库存额为( )① 5.2 ② 4.1 ③ 4.133 ④ 56、某商品销售量去年比前年增长10%,今年比去年增长20%,则两年平均增长( ) ① 14.14% ② 30% ③ 15% ④ 14.89%7、用“原资料平均法”测定季节变动,适合于( ) ① 有增长趋势的数列 ② 有下降趋势的数列 ③ 呈水平趋势的数列 ④ 各种季节数列8、某企业利税总额1998年比1993年增长1.1倍,2001年又比1998年增长1.5倍,则该企业利税总额这几年间共增长( )①(1.1+1.5)-1 ②(2.1×2.5)-1 ③(51.2×35.2)-1 ④(1.1×1.5)-19、已知某地粮食产量的环比发展速度1998年为103.5%,1999年为104%,2001年为105%,2001年对于1997年的定基发展速度为116.4%,则2000年的环比发展速度为( )① 103% ② 101% ③ 104.5% ④ 113%10、某地区连续五年的经济增长率分别为9%、7.8%、8.6%、9.4%和8.5%,则该地区经济的年平均增长率为( )① 5085.1094.1086.1078.109.1⨯⨯⨯⨯-1 ② 5085.0094.0086.0078.009.0⨯⨯⨯⨯③508509.1⨯⨯⨯④(9%+7.8%+8.6%+9.4%+8.5%)÷5⨯.1094.1078.1086.111、某校学生人数逐年增加,1992年比1991年增长8%,1993年比1992年增长7%,2001年比1993年增长56%,则年平均增长速度为()①356.1.008.1⨯⨯-1.10707⨯-1 ②1056.0.0⨯08③35608⨯-1 ④108.1⨯.1.10708⨯-1.1.1⨯56.10712、下列指标中,属于序时平均数的是()①某地区某年人口自然增长率②某地区某年人口增长量③某地区“八五”期间年均人口递增率④某地区人口死亡率13、某银行1月1日存款余额为102万元,1月2日为108万元,1月3日为119万元,则三天平均存款余额为()① 102/2+108+119/2 ②(102+108+119)÷3③(102/2+108+119/2)÷3 ④ 102+108+11914、要通过移动平均法消除季节变动,则移动平均项数N()①应选择奇数②应选择偶数③应和季节周期长度一致④可任意取值15、用原资料平均法求季节比率,第一步计算各年同期(月或季)平均数,是为了消除()①长期趋势②季节变动③循环变动④不规则变动16、计算平均发展速度的累计法,要求满足的条件是()①最末一期的推算水平与实际水平相等②各期推算水平与各期实际水平相等③ 0到n期的推算水平总和与0到n期的实际水平总和相等④ 1到n期的推算水平总和与1到n期的实际水平总和相等17、某产品单位成本从1990年到2001年的平均发展速度为98.5%,说明该产品单位成本()①平均每年降低1.5% ②平均每年增长1.5%③ 2001年是1990年的98.5% ④ 2001年比1990年降低98.5%18、时间数列中,各项指标数值可以直接相加的是()①时期数列②时点数列③相对数时间数列④平均数时间数列19、某地区1980年国内生产总值为60亿元,至2000年达到240亿元,则2000年在1980年的基础上()①翻了四番②翻了三番③增长了三倍④增长了四倍20、根据近几年数据计算所得,某种商品2季度销售量季节比率为1.6,表明该商品2季度销售()①处于旺季②处于淡季③增长了60% ④增长了160%二、多项选择题1、下列指标中分子为时期指标的有()①人均粮食产量②人均钢铁产量③平均分摊到每吨粮食上的水库容量数④平均分摊到每万人的零售商店数⑤平均分摊到每万元农业产值上的农业机械马力数2、直线趋势方程yˆ= a+b t中,b表示()①平均增长量②平均增长速度③平均发展速度④时间t每增加一个单位,现象y平均增加b个单位⑤现象y随着时间增长,每期以b的速度发展3、计算和应用平均速度指标应注意()①用分段平均速度补充总平均速度②联系每增长1%的绝对值进行分析③联系基期水平进行分析④结合环比发展速度进行分析⑤正确选择报告期水平4、平均增减量是()①各期累计增减量的平均②各期逐期增减量的平均③累计增减量÷逐期增减量个数④累计增减量÷(时间数列项数-1)⑤各期累计增减量之和÷逐期增减量个数5、下列属于时点数列的有()①某工业企业历年利税总额②某金融机构历年年末贷款余额③某商业企业历年销售额④某地区历年年末生猪存栏头数⑤某高校历年招生人数6、下列属于时期数列的有()①逐年的人口自然增长率②逐年的人口死亡率③逐年的人口增长量④逐年的人口出生数⑤逐年的人口死亡数7、逐期增长量和累计增长量之间有如下关系()①各逐期增长量的和等于相应时期的累计增长量②各逐期增长量的积等于相应时期的累计增长量③两相邻时期累计增长量之差等于相应时期的逐期增长量④两相邻时期累计增长量之商等于相应时期的逐期增长量⑤两相邻时期逐期增长量之差等于相应时期的累计增长量8、研究长期趋势的目的在于()①认识现象随时间演变的趋势和规律②为趋势预测提供必要条件③研究趋势变动的经济效果④分析趋势产生的原因⑤剔除趋势影响以分解数列中的其他因素9、从数据特征上判断,可以拟合指数曲线的时间数列应满足()①数列一次差大体相同②数列二次差大体相同③数列对数一次差大体相同④数列中各环比增长率大体相同⑤数列中各环比发展速度大体相同10、对于包含四个构成因素(T、S、C、I)的时间数列,以原数列各项数值除以移动平均值(其平均项数与季节周期长度相等)后所得比率()①只包含趋势因素②只包含季节因素③消除了趋势和循环因素④消除了趋势和不规则因素⑤包含季节和不规则因素三、判断分析题1、对于一个呈上升趋势的现象,其拟合的直线趋势方程yˆ= a+b t中,b肯定不会为0。
2、移动平均项数N越大,对数列中数据变化的反应就越灵敏。
3、季节比率大于1时,表明由于季节因素的影响使实际值高于趋势值。
四、简答题1、时间数列有哪些速度分析指标?他们之间存在怎样的关系?2、甲企业近四年产品销售量分别增长9%、7%、8%、6%,乙企业这四年产品的次品率也正好是9%、7%、8%、6%;这两个企业这四年的平均增长率和平均次品率是否也一样?为什么?3、测定长期趋势的移动平均法和趋势拟合法各有什么特点?五、计算题1、某汽车制造厂2000年产量为30万辆。
(1)若规定2001—2003年年递增率不低于6%,其后不低于5%,问2005年该厂汽车产量将达到多少?(2)若规定2010年汽车产量在2000年的基础上翻一番,而2001年的增长速度可望达到7.8%,问以后9年应以怎样的速度增长才能达到预定目标?(3)若规定2010年汽车产量在2000年的基础上翻一番,并要求每年保持7.4%的增长速度,问能提前多少时间达到预定目标?2、某地区社会商品零售额1986—1990年期间(1985年为基期)每年平均增长10%,1991—1995年期间每年平均增长8.2%,1996—2001年期间每年平均增长6.8%。
问2001年与1985年相比该地区社会商品零售额共增长多少?年平均增长速度是多少?若1995年社会商品零售额为30亿元,按此平均增长速度,2002年的社会商品零售额应为多少?问:五年间平均每年的增长速度是多少?超过平均增长速度的年份有哪些?二.多选题1.下面哪几项是时期数列()A.我国近几年来的耕地总面积B.我国历年新增人口数C.我国历年图书出版量D.我国历年黄金储备E.某地区国有企业历年资金利税率答案:B C2.时间序列的基本要素是()。
A.被研究现象或指标所属的时间B.该现象或指标在此时间坐标下的指标值C.按品质标志划分的各组D.按数量标志划分的各组E.被研究现象或指标所属的空间答案:A B3.对时间数列进行研究的意义,概括来讲就是:()。
A.决策B.信息C.反馈D.了解E.预测答案:D E4.时间数列按照其构成要素中统计指标值的表现形式,分为()。
A.绝对数时间数列B.相对数时间数列C.平均数时间数列D.等差时间数列E.等比时间数列答案:A B C5.下列属于时期序列的有()。
A.某省历年出生的婴儿数B.某省历年年末人数C.某省历年固定资产投资额D.某省全年城镇居民的月收入E.某省历年国内生产总值答案:A C D E6.在原始时间数列基础上派生的数列是()。
A.绝对数时间数列B.相对数时间数列C.平均数时间数列D.等差时间数列E.等比时间数列答案:B C7.编制时间序列的原则是()。
A.时间的可比性原则B.统计口径或总体范围的一致性C.经济内容的一致性D.计算方法的一致性E.计算单位的一致性答案:A B C D E8.分析时间数列的水平指标包括有()。
A.发展水平B.发展速度C.增长量D.平均发展水平E.平均增长量答案:A C D E9.将不同时期的发展水平加以平均而得到的平均数称为()。
A.序时平均数B.静态平均数C.动态平均数D.平均发展水平E.一般平均数答案:A C D10.发展速度和增长速度的关系是()。
A.环比发展速度=定基发展速度—1B.增长速度=发展速度—1C.定基增长速度的连乘积等于定基发展速度D.环比增长速度的连乘积等于环比发展速度E.定基增长速度=各环比发展速度的连乘积—1答案:B E11.若两个相邻时期的环比发展速度皆为103%,则()。