当前位置：文档之家 › 平行四边形复习课件(市级公开课)

平行四边形复习课件(市级公开课)

  • 格式：ppt
  • 大小：830.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

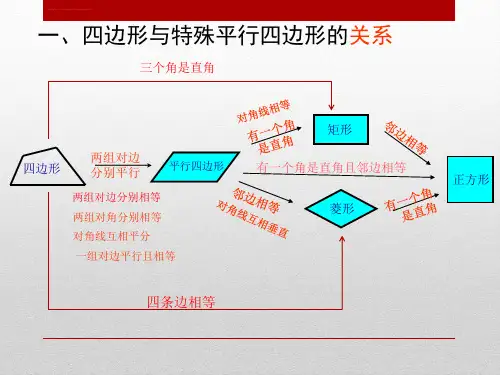
八年级数学平行四边形的复习课件ppt

八年级数学平行四边形的复习课件ppt
形．
证明：（1）在△ADE与△CDE中， AD＝CD，DE＝DE，EA＝EC， ∴△ADE≌△CDE， ∴∠ADE=∠CDE， ∵AD∥BC， ∴∠ADE=∠CBD， ∴∠CDE=∠CBD， ∴BC=CD， ∵AD=CD， ∴BC=AD， ∴四边形ABCD为平行四边形， ∵AD=CD， ∴四边形ABCD是菱形；
2.下列性质中，矩形不一定具有的是（ D ）。
(A)对角线互相平分且相等
(B)四个角相等
(C )既是轴对称图形，又是中心对称图形 (D)对角线互相垂直平分
3.菱形具有而一般平行四边形不一定具有的性质是（ C ）。
(A)对边相等。 （对C角）相对等角。线互相垂直。
(B) (D)对角线互相平分。
4.正方形具有而菱形不一定具有的性质是（ B ）。
(A)对角Байду номын сангаас互相平分。
(B)对角线
（相C等）。对角线平分一组对角。 (D)对角线互相垂直。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
（三）填空题：
1、如图(1)，
ABCD中，BE平分∠ABC，已知∠ABE＝25° 则∠C = 50° ∠D＝_1_3_0_°____
轴对称 中心对称
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
根据性质填空：
1.两条对角线 互相平分 2.两条对角线 相 等 3.两条对角线 互 相 垂 直 4.两条对角线 互相平分且相等
矩形 有一个角是直角且邻边相等

数学八年级下《平行四边形》复习课件

数学八年级下《平行四边形》复习课件

选择题:
2.平行四边形一边长为 10 ,则它的两条 对角线可以是( C ) A、6 ,8 B、8, 12
C、8, 14
D、6, 14
如图， ABCD的周长为２０cm, O是对角线AC和BD的交点 （１）若△ABC的周长是７cm,求 OC的长 （２）若△OAB的周长比△OBC的 周长短４cm，求AB的长
对角线: 4.对角线互相平分的四边形是平行四边形
角:
5.两组对角分别相等的四边形是平行四边形
（注：第５条不能直接应用）
A B C
D
两组对边分别平行
？
B
A
D C
2.平行四边形的识别方法： （1）∵AD//BC，AB//CD ∴四边形ABCD是平行四边形 （2）∵AD// BC，AD=BC ∴四边形ABCD是平行四边形 （3）∵AD=BC ，AB=DC ∴四边形ABCD是平行四边 形（4）∵∠A=∠C，∠B=∠D ∴四边形ABCD是平行四边形 （5）∵OA=OC，0B=0D ∴四边形ABCD是平行四边形
☆定义：两组对边分别 平行 的四 边形是平行四边形。 ☆性质： 1、平行四边形对边 平行且相等 2、平行四边形对角 相等 互补 邻角 3、平行四边形对角线 互相平分
4、平行四边形是中心对称图形
边： 1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形 3.一组对边平行且相等的四边形是平行四边形
已知E、F是
ABCD边AD、BC的中点
求证：BE=DF。
A E D
B
F
C
已知:点D、E、F分别在△ABC的边BC、 AB、AC上，且DE∥AF，DE=AF，G在 FD的延长线上，DG=DF。
求证：AG与ED互相平分。

平行四边形复习课件

平行四边形复习课件

一组对边平行且相等的四边形是平行四边 形。
两组对角分别相等的四边形是平行四边形 。
02
平行四边形的特殊形式
矩形
01 定义
有一个角是直角的平行四边形是矩形。
02 性质
矩形的四个角都是直角，矩形的对角线相等。
03 判定
有一个角是直角的平行四边形是矩形；对角线相 等的平行四边形是矩形。
菱形
01 定义
矩形、菱形、正方形的判定方法与证明思路
正方形的判定方法与证明思路
正方形是特殊的长方形和菱形，其判 定方法有五种。
正方形的判定方法主要有五种，一是 有一组邻边相等且有一个角是直角的 平行四边形是正方形；二是有一个角 是直角的菱形是正方形；三是有一个 角是直角的矩形是正方形；四是有一 组邻边相等的矩形是正方形；五是有 一个角是直角的等腰梯形是正方形。 在证明过程中，需要结合已知条件， 通过全等三角形、平行线的性质等定 理进行证明。
2. 举例说明：例如，我们要证明四边形ABCD是平行 四边形，那么我们需要证明AB//CD且AB=CD。
总结词：如果一个四边形的一组对边平行且相 等，那么这个四边形是平行四边形。
1. 介绍利用一组对边平行且相等证明平行四边形 的方法：一组对边平行且相等的四边形是平行四 边形。
06
典型例题解析与拓展
矩形、菱形、正方形的判定方法与证明思路
01
菱形的判定方法与证明思路
02
菱形是平行四边形的一个特例，其判定方法有三种。
03
菱形的判定方法主要有三种，一是有一组邻边相等的平行 四边形是菱形；二是有一个角是直角的菱形是菱形；三是 有一组邻边相等的矩形是菱形。在证明过程中，需要结合 已知条件，通过全等三角形、平行线的性质等定理进行证 明。

平行四边形市公开课获奖课件省名师示范课获奖课件

平行四边形市公开课获奖课件省名师示范课获奖课件

A
D
B
EC
A
D
E
B
C
图（1）
初三数学备课组
初中数学【一轮能复力习提升】
例3.如图，已知□ABCD中，点E为BC边
旳中点，延长DE,AB相交于点F．求证： CD=BF．
CD
ABF
初三数学备课组
初中数学一【轮思复习维拓展】
学以致用
例4.用长为12 m旳篱笆，一边利用足够长旳墙
围出一块苗圃．如图，围出旳苗圃是五边形 ABCDE，AE⊥AB，BC⊥AB， ∠C=∠D=∠E．设CD=DE=x m，五边形
3.平行四边形被提成如图③旳 四块,分别记为S1,Ｓ2,S3,S4 则它们旳关系是 S1+S3=S2+.S4
初三数学备课组
初中数学一轮复习
6、已知点A(3,0),B(-1,0),C(0,2),以A,B,C为
顶点画平行四边形,则第四个顶点D旳坐标
为 (4,2) , (2,-2) , (-4,2)
.
y
初中数学一轮复习
平行四边形
初三数学备课组
初中数学一轮复习
【概念解读】
一、四边形旳概念 1.定义：在同一平面内，由不在同一直线 上旳四条线段首尾顺次相接构成旳图形. 2.四边形旳内角和与外角和均为360°. 3.四边形具有不稳定性. 4.多边形内角和定理：n边形旳内角和等于 (n-2)·180° 5.多边形外角和定理：n边形旳外角和等于 360°. 6.多边形旳对角线.
初中数学一轮复习
平行四边形被分割后各部分之间旳关系
S1 S4 S2 S3
①
S1 S4
S2 S3
②
S1 S4 S2
S3
③
1.平行四边形被提成如图①旳 四块,分别记为S1,Ｓ2,S3,S4 则它们旳关系是 S1Ｓ3.=S2S4

平行四边形复习课课件

平行四边形复习课课件

2
周长与面积的换算
在实际应用中，有时需要根据平行四边 形的面积来估算其周长，或者根据周长 来估算其面积。这需要一定的经验和数 学技巧。
3
面积与周长的应用
平行四边形的面积和周长在实际生活中 有着广泛的应用，如建筑设计、土地测 量、木材加工等。了解它们的计算方法 和关系对于解决实际问题非常重要。
04
平行四边形的应用
探究题
在解决实际问题时，如何应用平行四边形的 性质？
开放题
设计一个与平行四边形相关的实际问题，并 给出解决方案。
感谢您的观看
THANKS
分类
总结词
平行四边形的分类
详细描述
平行四边形可以分为以下几种类型：矩形、菱形、正方形等。
02
平行四边形的判定
定义法
01
02
03
总结词
根据平行四边形的定义来 判断
详细描述
平行四边形的定义是两组 相对边平行，因此，如果 一个四边形两组相对边平 行，则它是平行四边形。
示例
在四边形ABCD中，如果 AB平行于CD且AD平行于 BC，则四边形ABCD是平 行四边形。
周长计算
周长公式
平行四边形的周长等于四边之和，即周长 = 边1 + 边2 + 边3 + 边4。
周长计算方法
分别测量平行四边形的四条边，然后加起来 得到周长。
周长计算注意事项
确保测量的边是平行四边形的有效边，不能 遗漏或重复计算。
面积与周长的关系
1
面积与周长的关系
一般来说，平行四边形的面积越大，其 周长也越大。这是因为面积较大的平行 四边形往往需要更长的边来支撑更大的 面积。
示例
在四边形ABCD中，如果 角A和角B相等，且角C和 角D相等，则四边形ABCD 是平行四边形。

平行四边形复习(全章)PPT课件

平行四边形复习(全章)PPT课件

A 3x E 2x D
A x D 2x
E
3X
3x
B
C
B精选
C
精选
小题多练
精选
思考
折叠问题
1、在矩形ABCD中，AB=16，BC=8.
将矩形 沿AC折叠，点D落在点E处，且
CE交AB于点F，求AF的长.
点拨：对于折叠 D
C
问题，可以从折叠前
后的两个图形是全等 图形入手进行分析.
A
B
F
精选
E
1、矩形具有而一般的平行四边形不具有的性质是( C )
（1）当∠BAC等于 150°时，四边形ADFE是矩形； （2）当∠BAC等于 60°时，平行四边形ADFE不存在；
（3）当△ABC分别满足什么条件时，平行四边形是菱形、正方形.
解:（3) AB=AC时，平行四边形ADFE时菱形。 AB=AC且∠BAC=150°时，平行四边形ADFE是正方形。
F D
A
D
O
E
B
C
精选
1、 已知菱形ABCD的周长为20cm。 ∠A：∠ABC=1：2 ，则对角线BD的 长等于______5____cm。 2、正方形的两条对角线的和为8cm， 它的面积为______平3方2 厘米
精选
（三）填空题
相信自 己，你 是最棒
的
1、菱形的周长为32cm，若有一个内角为120°，
于O点，且AB≠BC，过O点作OE⊥AC，交BC
于E，如果△ABE的周长为b，则平行四边形
ABCD的周长是（ ）C
A. b B. 1.5b C. 2b
A
D
D. 3b
O
B
E
精选C
相信自己，你 是最棒的！！

平行四边形复习课 公开课教学课件

平行四边形复习课 公开课教学课件

第十八章　平行四边形复习课（一）——平行四边形的性质与判定问题导入已知：如图，四边形AEFD和EBCF都是平行四边形，求证：四边形ABCD是平行四边形学习目标　2.梳理知识点　一　两组对边分别平行的四边形叫做平行四边形。

　二　（1）看边：①平行四边形的对边平行　②平行四边形的对边相等　（2）看角：①平行四边形的对角相等 ②平行四边形的邻角互补　（3）看对角线：Ｏ学会分类归纳　平行四边形的对角线互相平分　例题：已知□ABCD 中，CE 平分∠BCD，且交AD 于点E ， 若∠1＝65°,求∠B 的大小学以致用思考：平行四边形的性质可以为三角形全等的证明提供哪些条件？ 点拨：平行四边形的性质为三角形全等的证明提供了边相等和角相等的条件. 变式：已知□ABCD 中，CE 平分∠BCD，且交AD 于点E ， 若AF ‖CE ,且交BC 于点F，　求证：ΔABF ≌ ΔCDE梳理知识点　三　①两组对边分别平行的四边形是平行四边形 ②两组对边分别相等的四边形是平行四边形 ③一组对边平行且相等的四边形是平行四边形　两组对角分别相等的四边形是平行四边形　两条对角线互相平分的四边形是平行四边形Ｏ还是分类归纳　（1）从边来判：　（2）从角来判：　（3）从对角线来判：小组合作要求：每个小组至少写出两种方法　如图，将□ABCD的对角线BD向两个方向延长分别至点E和点F ，且使BE＝DF，。

　求证：四边形AECF是平行四边形Array思考：如何选取适当的判定定理证明四边形是平行四边形？ 点拨：根据不同条件灵活选取适当的判定定理进行推理论证.1.已知□ABCD 中，若∠A +∠Ｃ=120°,则∠Ｂ的度数是（　） Ａ.100° Ｂ.120° Ｃ.80° Ｄ.60°B A4.如图，在平行四边形ABCD中，E,F分别为AB，CD的中点，连接DE,EF,FB,则图中共有平行四边形的个数（平行四边形ABCD除外）为（　）个　　Ａ.1 Ｂ.2 Ｃ.3 Ｄ.4C 3.如图，在□ABCD中，∠A的平分线AE交CD于E , AB=5,BC=3,则EC的长为 。

平行四边形复习课件公开课

平行四边形复习课件公开课
答案8
平行四边形在日常生活中有广泛的应用，如门窗的设计、桌 椅的摆放、海报的制作等。平行四边形具有相对稳定的特性 ，因此在许多实际场景中都有应用。
THANKS FOR WATCHING
感谢您的观看
矩形的面积和周长可以通过长和宽来 计算，菱形的面积和周长也可以通过 边长来计算。
菱形是四边相等的平行四边形，其对 角线互相垂直且平分，具有中心对称 性。
正方形
正方形是特殊的平行 四边形，其四边相等 且四个角都是直角。
正方形的面积和周长 可以通过边长来计算， 是几何中最完美的形 状之一。
正方形的对角线相等 且互相垂直平分，具 有轴对称性和中心对 称性。
平行四边形复习课件公开课
contents
目录
• 平行四边形的基本性质 • 平行四边形的判定 • 平行四边形的特殊情况 • 平行四边形的实际应用 • 复习题与答案
01 平行四边形的基本性质
定义与性质
总结词
理解平行四边形的定义和基本性质，包括对 边平行、对角相等、对角线互相平分等。
详细描述
平行四边形是一种常见的几何图形，具有一 系列独特的性质。首先，平行四边形的定义 是两组相对边平行，这使得它成为一种特殊 的四边形。其次，平行四边形具有一些基本 的性质，如对角线互相平分、对角相等、邻 角互补等。这些性质在解决几何问题时非常 有用，可以帮助我们证明一些重要的结论。
平行四边形在数学问题中也有着 广泛的应用，它可以作为解决几
何、代数等问题的工具。
在几何问题中，平行四边形可以 用于证明定理、求解角度、计算
面积等。
在代数问题中，平行四边形可以 用于求解方程、不等式等，提供
更简便的解题方法。
其他领域的应用
01
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

20cm,若△OAD的周长为17cm，则AD=__7__cm
D
C
平行四边形的对角线互相平分
O
A
B
达标体验
1.已知 ABCD,若OA=1cm, OB=2cm, ∠BAC=90°
（1）CD=___3_cm;
（2）若∠CAD=30°,∠BCD=_1_2_0__°, ∠ADC=__6_0__°.
A
D
（3）AC=__2__cm,BD=__4__cm;
A
E
F
B
D
C
思想篇
变式1.如图，△ACD， △ABE,△BCF均为直线BC同 侧的等边三角形，当 AB≠AC时，证明：四边形 ADFE为平行四边形.
E D
A
F
变式2.平面上三个等边三 角形△ACE、△ABD， △BCF，两两共有一个顶 点，如图所示，求证：CD 与EF互相平分
B
C
F
B
C
E
D
A
思考题
欢迎进入 平行四边形世界
桐乡十中 刘绵福
请你填一填
1、已知 ABCD,若AB=15㎝, BC=10cm
则AD= 10 ㎝.周长= 50 cm.
平行四边形的两组对边分别相等 D
C
2、已知 ABCD, ∠A=50度, A
B
则∠C= 50 度. ∠B= 130 度.
平行四边形的对角相等、邻角互补
3、如图， ABCD的对角线AC、BD长度之和为
A
D
E
A 3x E 2x D x
2x
3x
3x
B
C
B
C
拓展提高
如图，已知AB＝AC，B是AD的中 点，E是AB的中点． 求证：CD＝2CE． C
A EB D
F
丰 收园
通过这节课的复习， 你又增加了哪些收获？ 能与大家一起分享吗？
思考题
如图，已知△ABC和△ADE都是等边三角 形,点D在BC上，AB边上有一点F，且 BF=DC,连接CF，证明：CF与DE互相平行.
AB+CD的长? D
C
O
B
A
链接中考
1.（2008年河北省中考题）如图，若□ABCD与□EBCF关于
直线BC对称，∠ABE＝90°，则∠F ＝__4_5__°．
8 2、已知 ABCD,若AC=20㎝,BD=16cm,OA=1__0_cm,OB=___cm．
3、（浙江金华中考题）国家级历史文化名城——金华，风光秀丽，花木葱
y
3
(-3,2)
2A
1
OO
-4 -3 -2 -1
1
-1
-2
-3
(3,2)
B
2 题中，再作一条直线L，解析式为y=-2x+2，设点 M为直线L上一点，过点M作AB的平行线，交y轴于点N， 是否存在这样的点M，使得以M、N、A、B为顶点的四 边形是平行四边形？若存在，请求出符合条件的点M的 坐标；若不存在，请说明理由。 y
L
3
2A
1
O
B
-4 -3 -2 -1 O 1 2 3 4 x
-1
-2
-3
y
M
(-3,8)
6N
y=-2x+2
5
4
MN在AB上方
3
2A
1
O
-4 -3 -2 -1 O 1 -1
MN在AB下方
-2 N -3
-4
B
2 3 4x
M (3,-4)
如图，在 ABCD中，E、F、G、H 分
别是各边上的点，且AE=CF，
BG=DH。
求证：EF与GH互相平分。
D
FC
H
G
AE
B
小试牛刀
已知：AD为△ABC的角平分线， DE∥AB ，在AB上截取BF＝AE。 求证：EF＝BD
A
12
F
E
3
B
D
C
小试牛刀
如图，AD、BC垂直相交于点O，
AB∥CD，BC=8，AD=6，求
4.（福建龙岩）如图（3），在□ABCD中，E、F 分别为AD、BC边上的一点，若再增加一个条件
DE=BF _____________，就可推得BE = DF． 或AE=CF 或BE∥DF
链接中考
□ABCD的周长为32cm, ∠ABC的角平分
线交边AD所在直线于点E，且AE:ED =3：2，则AB＝____6_c_m_或__1_2_c_m__．
O
B
C
请你挑一挑
在四边形ABCD中,若分别给出六个
条件:①AB∥CD ②AD=BC ③
OA=OC ④AD∥ BC ⑤
AB=CD ⑥OB=OD. 现在,以其中
的两个为一组,能直接确定四边形
ABCD为平行四边形的条件是 _________
(只填序号)
D
C
O
A
B
☆平行四边形的判定：
边： 1.两组对边分别平行的四边形是平行四边形
茏．某广场上一个形状是平行四边形的花坛（如图），分别种有红、黄、
蓝、绿、橙、紫6种颜色的花．如果有AB//EF//DC，BC//GH//AD，那么下列
C 说法中错误的是（ ） A．红花、绿花种植面积一定相等 B．紫花、橙花种植面积一定相等 C．红花、蓝花种植面积一定相等 D．蓝花、黄花种植面积一定相等
在ABCD中，分别为边向内作等边△ADE 和△BCF，连接BE、DF，求证：四边形 BEDF是平行四边形.
D
C
F
E
A
B
初露锋芒
如图，Rt△OAB的两条直角边在坐标轴上，已
知点A（0，2），点B（3，0），则以点O,A,B
为其中三个顶点的平行四边形的第四个顶点C的
坐标为 。 _________________
2.两组对边分别相等的四边形是平行四边形 3.一组对边平行且相等的四边形是平行四边形
对角线: 4.对角线互相平分的四边形是平行四边形
探究应用一
☆找平行四边形
已知： ABCD中，直线MN//AC，分
别交DA延长线于M，DC延长线于N，
AB于P，BC于Q。 求证：PM=QN。
M
A
D
P
B
Q
C
N
探究应用二 ☆构造平行四边形