(含答案)空气比热容比

空气比热容比的测定一、实验目的1.学习测量理想气体比热容比的原理和方法。

2.测量空气的比热容比。

二、实验仪器实验台，590AD 温度计模块，空气比热容比实验仪。

三、实验原理气体的定压比热容P C 与定容比热容V C 之比称为气体的比热容比，用符号r 表示，它被称为气体的绝热系数，是一个很重要的参量，经常出现在热力学方程中。

通过测量r ，可以加深对绝热、定容、定压、等温等热力学过程的理解。

对于理想气体：R C C V P =- （5-1）其中，R 为气体的普适常数。

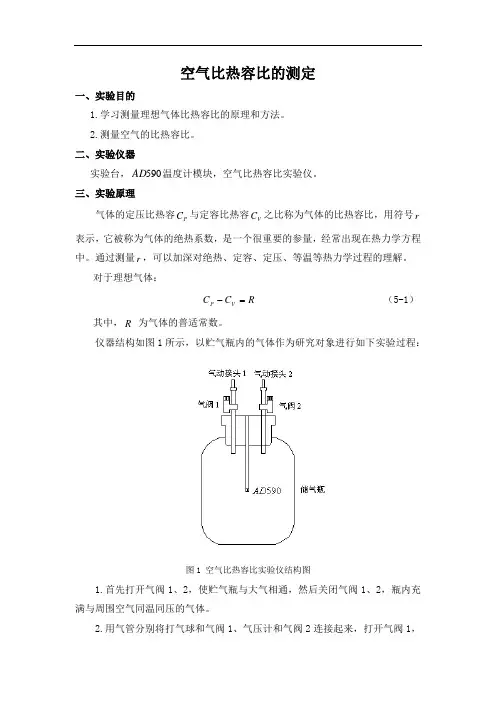
仪器结构如图1所示，以贮气瓶内的气体作为研究对象进行如下实验过程：图1 空气比热容比实验仪结构图1.首先打开气阀1、2，使贮气瓶与大气相通，然后关闭气阀1、2，瓶内充满与周围空气同温同压的气体。

2.用气管分别将打气球和气阀1、气压计和气阀2连接起来，打开气阀1，用打气球向瓶内打气，充入一定量的气体，然后关闭气阀1。

此时瓶内原来的气体被压缩，压强增大，温度升高。

等待内部气体温度稳定，即达到与周围温度平衡，此时气体处于状态),,(011T V P I3.将连接在气阀1上的气管取下，迅速打开放气阀，使瓶内的气体与大气相通，当瓶内压强降到0P 时，立即关闭放气阀，将有体积为V ∆的气体喷泻出贮气瓶。

由于放气过程较快，瓶内的气体来不及与外界进行热交换，可以认为是一个绝热过程。

在此过程中作为研究对象的气体由状态),,(011T V P I 转变为状态),,(120T V P II4.由于瓶内温度1T 低于外界温度0T ，所以瓶内气体慢慢的从外界吸热，直到达到外界温度0T 为止，此时瓶内的压强也随之增大为2P ，即稳定后的气体状态为),,(022T V P III 。

从状态Ⅱ到状态Ⅲ为等容吸热过程。

气体的状态变化过程如图2所示：图2 气体的状态变化过程曲线II I →为绝热过程，有绝热过程方程得：rr V P V P 2011= （5-2）III I →为等温过程，由等温过程方程得：2211V P V P = （5-3）由（5-2）（5-3）可得：2101ln ln ln ln P P P P --=γ （5-4）由（5-4）可以看出只要测得0P ，1P ，2P 就可以得空气的比热容比r 。

空气比热容比的测量实验报告一、实验目的1、了解绝热膨胀法测量空气比热容比的原理和方法。

2、学习使用绝热膨胀法测量空气比热容比的实验仪器。

3、掌握数据处理和误差分析的方法，提高实验技能和科学素养。

二、实验原理比热容比γ定义为气体的定压比热容Cp与定容比热容Cv之比，即γ ＝ Cp ／ Cv。

对于理想气体，γ是一个常数。

在本实验中，采用绝热膨胀法测量空气的比热容比。

实验装置主要由贮气瓶、U 形管压强计、打气球、阀门等组成。

首先，向贮气瓶内打入一定量的气体，使其压强达到一个较高的值P1。

然后迅速打开阀门，让气体绝热膨胀，此时瓶内气体的温度迅速降低，压强也随之下降到 P2。

由于过程绝热，满足绝热方程：P1V1^γ ＝P2V2^γ ①同时，根据波义耳定律，在等温过程中有：P1V1 ＝ P2V2 ②由①②两式可得：γ ＝ ln(P1 ／ P2) ／ ln(V2 ／ V1)在实验中，通过测量贮气瓶内气体压强的变化 P1 和 P2，以及相应的体积变化 V1 和 V2，就可以计算出空气的比热容比γ。

三、实验仪器1、贮气瓶：用于储存实验气体。

2、 U 形管压强计：测量贮气瓶内气体的压强。

3、打气球：向贮气瓶内打气。

4、阀门：控制气体的进出。

四、实验步骤1、实验前准备检查实验仪器是否完好，U 形管压强计中的液面是否平衡。

用打气球向贮气瓶内缓慢打气，使 U 形管压强计中的液面高度差达到一定值（例如 50cm 左右），记录此时的压强 P1。

2、绝热膨胀过程迅速打开阀门，让气体绝热膨胀，观察 U 形管压强计中液面的变化，待液面稳定后，记录此时的压强 P2。

3、重复实验重复上述步骤 5 6 次，以减小测量误差。

4、数据处理根据测量得到的 P1、P2 值，计算出每次实验的比热容比γ。

求平均值，并计算相对误差。

五、实验数据记录与处理｜实验次数｜ P1（cmHg）｜ P2（cmHg）｜γ ｜｜：：｜：：｜：：｜：：｜｜ 1 ｜ 525 ｜ 382 ｜ 142 ｜｜ 2 ｜ 518 ｜ 375 ｜ 143 ｜｜ 3 ｜ 532 ｜ 388 ｜ 141 ｜｜ 4 ｜ 520 ｜ 378 ｜ 142 ｜｜ 5 ｜ 528 ｜ 385 ｜ 141 ｜｜ 6 ｜ 530 ｜ 386 ｜ 142 ｜平均值：γ ＝（142 ＋ 143 ＋ 141 ＋ 142 ＋ 141 ＋ 142）／ 6 ＝ 142理论值：空气的比热容比γ约为 140相对误差：E ＝（142 140）／ 140 × 100% ＝ 143%六、误差分析1、实验过程中，气体并非完全绝热，存在一定的热交换，导致测量结果偏大。

空气比热容比的测定气体的定压比热容C P 和定容比热容C V 之比⎪⎪⎭⎫⎝⎛=V P C C γ称为气体的比热容比。

γ是一个常用的物理量。

在描述理想气体的绝热过程时，γ成为了联系各个状态参量（P 、V 和T ）的关键参数：（绝热过程，P 、V 之间满足关系：） C PV =γ （1） 气体的比热容比γ除了在理想气体的绝热过程的过程方程中起重要作用之外，它在热力学理论及工程技术的实际应用中也有着重要的作用，例如热机的效率、声波在气体中的传播特性都与之相关。

γ的测量方法很多，传统测量方法是热力学方法[1]（绝热膨胀法）来测量，其优点是原理简单，而且有助于加深对热力学过程中状态变化的了解，但是实验者的操作技术水平对测量数据影响很大，实验结果误差较大。

本实验采用振动法[2]来测量，即通过测定物体在特定容器中的振动周期来推算出γ值）。

振动法测量具有实验数据一致性好，波动范围小，误差较小等优点。

[ 实验目的 ]（1）学习用振动法测定空气的比热容比。

（2）练习使用物理天平、螺旋测微器、数字式周期记录仪、大气压计等。

[ 实验原理 ]图-1 图-2实验装置如图-1所示。

本实验以贮气瓶Ａ内的空气作为研究的热力学系统。

在贮气瓶Ａ正上方连接玻璃细管Ｂ，并且其内有一可自由上下活动的小球Ｃ，由于制造精度的限制，小球和细管之间有0.01mm 到0.02mm 的间隙。

为了弥补从这个小间隙泄漏的气体，通过气泵持续地从贮气瓶的另一连接口Ｄ注入气体，以维持瓶内的压强保持恒定。

适当调节气泵输出的流量，可以使小球在玻璃细管Ｂ内（中央一侧有一小孔K 附近，如图-2所示）在竖直方向上来回振动：当小球在小孔K 的下方并向下运动时，贮气瓶中的气体被压缩，压强增加；而当小球经过小孔向上运动时，气体由小孔膨胀排出，压强减小，小球又落下。

其振动周期可利用周期记录仪测量出来。

若小球质量为m ，直径为d ，当其出于平衡状态时，瓶内气压P 和大气压强0P 之间满足关系：20)2/(d mgP P π+= （2）当小球由平衡位置向下运动一个小距离x ，这导致贮气瓶内的压强变化dP ，从而小球所受合力F 为：dP d F 2)2/(π= （3）由牛顿运动方程ma F =，得：222)2/(dtxd m dP d =π （4）另一方面，由于小球振动很快，可以近似作为绝热过程处理，于是贮气瓶内气体的压强P ，直和体积V 满足（1）式的绝热方程。

气体在不同的状态过程中，温度变化相同，所吸收（放出）的热量是不同的。

在等压过程中，一摩尔气体温度升高（降低） 1k时，所吸收（放出）的热量称为定压摩尔热容量，以Cp表示；在等容过程中，一摩尔气体温度升高（降低）1k时所吸收（放出）的热量称为定容摩尔热容量以Cv表示。

因此可以定义＝，我们称之为比热容比，当将空气视为理想气体时＝ 1.40湿比热容以单位千克绝干气体为基准，将（ 1+H）kg 湿空气温度升高或降低 1oC所需要吸收或放出的热量，称为湿空气的比热容，简称湿比热容，用cH表示，单位为kJ/(kg 干空气 .K)cH=ca+cvH (12-9)式中， ca—干空气的比热容， kJ/(kg.K);cv —水汽的比热容， kJ/(kg.K).在常用的温度范围内， ca≈ 1.01kJ(kgK),cv ≈ 1.88kJ(kgK), 将这些数据代入式（ 12—9），得CH=1.01+1.88H（12— 10）上式表明，湿比热容只是温度的函数空气的密度大小与气温等因素有关，我们一般采用的空气密度是指在标准状态下，密度为 1.29 千克每立方米，空气的压力大小与大气压与受力面有关，我估计楼主问的是空气的压强吧？在标准状态下，大气压强 76CM汞柱高！你也可以换算成其它单位。

空气的浓度这个概念一般很少采用，严格意义上可以理解为每立方米空气的质量，这与空气密度是一个概念。

在气象上，空气有湿度一说，那是指空气中的含水量，湿度越大，说明空气中的水份越高。

自下而上来看，为对流层，平流层，中间层，暖层，散逸层．自地球表面向上，随高度的增加空气愈来愈稀薄。

大气的上界可延伸到 2000～3000 公里的高度。

在垂直方向上，大气的物理性质有明显的差异。

根据气温的垂直分布、大气扰动程度、电离现象等特征，一般将大气分为五层。

对流层对流层是大气的最下层。

它的高度因纬度和季节而异。

就纬度而言，低纬度平均为 17～ 18 公里；中纬度平均为 10～12 公里；高纬度仅 8～9 公里。

空气比热容比的测定1、学会一种测定空气比热容比的方法。

2、学会正确使用物理天平和千分尺。

3、掌握直接测量值和间接测量值不确定度的计算。

1、千分尺和物理天平的正确使用方法。

2、气体比热容比的概念和不确定度的计算。

讲解、讨论与演示相结合。

3学时。

比热容是物质的重要参量，在研究物质结构、确定相变、鉴定物质纯度等方面起着重要的作用。

气体的定压比热容和定体比热容的比值v p C C 称为比热容比γ。

气体的γ值在许多热力学过程特别是绝热过程中是一个很重要的参数。

实验中气体的比热容比常通过绝热膨胀法、绝热压缩法等方法来测定。

本实验将采用一种比较新颖的方法，即通过测定小球在储气瓶玻璃管中的振动周期来计算空气的γ值。

一、实验目的1、学会一种测定空气比热容比的方法。

2、学会正确使用物理天平和千分尺。

3、掌握直接测量值和间接测量值不确定度的计算。

二、实验仪器FB212型气体比热容比测定仪、支撑架、小型气泵、TW-1型物理天平、0-25mm 外径千分尺等。

FB212型气体比热容比测定仪的结构和连接方式如图2所示：三、实验原理如图1所示，钢球A 位于精密细玻璃管B 中，其直径仅仅 比玻璃管直径小0.01-0.02mm ，使之能在玻璃管中上下移动， 瓶上有一小孔C ，可以通过导管将待测气体注入到玻璃瓶中。

设小球质量为m ，半径为r ，当瓶内气压P 满足下式时， 小球处于平衡位置：2rmgP P L π+= （2） 设小球从平衡位置出发，向上产生微小正位移x ，则瓶内气体的体积有一微小增量：x r dV 2π= （3）与此同时瓶内气体压强将降低一微小值dP ，此时小球所受合外力为：dP r F 2π= （4）小球在玻璃管中运动时，瓶内气体将进行一准静态绝热过程，有绝热方程：C PV =γ （5）两边微分，得01=+-PdV V dP V γγγ （6）将（3）、（4）两式代入（6）式，得：图1x VPr F 42γπ-= （7）由牛顿第二定律，可得小球的运动方程为：04222=+x mV Pr dt x d γπ （8）可知小球在玻璃管中作简谐振动，其振动周期为：4Pr22γωπmVT ==（9） 最后得气体的γ值为：pd T mVP r T mV 4242644==γ （10） （10）式中右边各量可以方便测出，故可以计算出气体的γ值。

实验五空气比热容比的测定气体的比热容比γ（亦称绝热指数），是一个重要的热力学参量。

测量γ值的方法有多种，绝热膨胀测量γ是一种重要的方法。

传统的比热容比实验大多是利用开口U 型水银压力计测量气体的压强，用水银温度计测温度，测量结果较为粗略。

本实验采用的是高灵敏度的硅压力传感器和高灵敏温度传感器，分别测量气体的压强和温度，克服了原来实验中的不足，实验时能更明显地观察分析热力学现象，实验结果较为准确。

【实验目的】1、 学习用绝热膨胀法测定空气的比热容比γ；2、观察和分析热力学系统的状态和过程特征，掌握实现等值过程的方法。

*3、了解硅压力传感器的工作原理，掌握其使用方法。

【实验原理】一 测量比热容比的原理单位质量（1kg ）的物质温度升高(或降低)1℃所吸收(或放出)的热量称为这种物质的比热容。

同一种气体由于受热过程不同，有不同的比热容。

对应于气体受热的等容过程及等压过程，气体的比热容有定容比热容C V 和定压比热容C P 。

定容比热容是将气体在保证体积不变的情况下加热，当温度升高1 ℃时所需的热量；而定压比热容则是在保持压强不变的情况下加热，温度升高1℃所需的热量。

显然，对同一种气体C P >C V ,因为定压膨胀过程要对外做功。

{对理想气体C P －C V =R, R=8.31J/mo l ·k,为气体普适恒量}。

通常称γ=C P /C V 为该气体的比热容比。

理想气体的压强p 、体积V 、温度T ，在任何状态下都遵守气态方程C TpV 常量=。

此外，在准静态绝热过程中还遵守绝热过程方程C pV '=γ。

因此γ亦称为绝热指数。

γ的大小与气体种类有关，还与温度有关。

对同一种气体，在常温下γ基本不随温度变化。

测量装置如图示（见实物）。

以储气瓶内空气作研究的热力学系统，进行如下实验过程。

（1） 首先打开放气阀A ，储气瓶与大气相通，再关闭阀 A ；瓶内充满与外界同温、同压气体。

空气比容与比热容
标题：“空气的比容与比热容”
空气是地球大气中的主要成分之一，它的比容和比热容是研究空气性质的重要参数。

本文将介绍空气的比容和比热容的概念、计算方法以及其在实际应用中的意义。

首先，空气的比容指的是单位质量空气在压力不变的情况下，温度变化时体积的变化量。

比容可以用下式表示：
β=ΔV/ΔT
其中，β表示比容，ΔV表示温度变化时的体积变化量，ΔT表示温度的变化量。

空气的比容与温度有关，通常情况下，温度升高，空气的比容增大；温度降低，空气的比容减小。

这是由于温度升高会使分子运动加剧，分子间的相互作用力减弱，从而导致体积的增大。

其次，空气的比热容指的是单位质量空气在压力不变的情况下，温度变化时吸收或释放的热量。

比热容可以用下式表示：
C=Q/(m*ΔT)
其中，C表示比热容，Q表示吸收或释放的热量，m表示单位质量空气的质量，ΔT表示温度的变化量。

空气的比热容与温度也有关系，通常情况下，温度升高，空气的比热容减小；温度降低，空气的比热容增大。

这是由于温度升高会加剧空气分子的振动和旋转，使得吸热能力减弱。

空气的比容和比热容在实际应用中具有重要的意义。

比容的计算可以用于气体的压缩、膨胀等过程的分析和设计。

比热容的计算可以用于理解和研究气体的热力学性质，例如在空调系统中，通过热交换器的设计来控制空气的温度。

总结而言，空气的比容和比热容是研究空气性质的重要参数，它们与温度密切相关，并在实际应用中发挥着重要的作用。

通过了解和掌握空气的比容和比热容，我们可以更好地理解和应用空气的性质，为相关领域的研究和实践提供有力支持。

实验5—2 空气比热容比的测定理想气体的定压比热容C p 和定容比热容C v 之间满足关系：p v C C R -=，其中R 为气体普适常数；二者之比p v C C γ=称为气体的比热容比，也称气体的绝热指数，它在热力学理论及工程技术的实际应用中起着重要的作用，例如：热机的效率及声波在气体中的传播特性都与空气的比热容比γ有关。

【实验目的】⒈ 用绝热膨胀法测定空气的比热容比。

⒉ 观测热力学过程中的状态变化及基本物理规律。

⒊ 学习空气压力传感器及电流型集成温度传感器的原理和使用方法。

【实验原理】把原处于环境压强P 0及室温T 0下的空气状态称为状态O (P 0 ，T 0)。

关闭放气阀、打开充气阀，用充气球将原处于环境压强P 0、室温T 0状态下的空气经充气阀压入贮气瓶中。

打气速度很快时，此过程可近似为一个绝热压缩过程，瓶内空气压强增大、温度升高。

关闭进气阀，气体压强稳定后，达到状态Ⅰ(P 1 ，T 1 )。

随后，瓶内气体通过容器壁和外界进行热交换，温度逐步下降至室温T 0，达到状态Ⅱ(P 2 ，T 0 ),这是一个等容放热过程。

迅速打开放气阀，使瓶内空气与外界大气相通，当压强降至P 0时立即关闭放气阀。

此过程进行非常快时，可近似为一个绝热膨胀过程，瓶内空气压强减小、温度降低；气体压强稳定后，瓶内空气达到状态Ⅲ(P 0 ，T 2 )。

随后，瓶内空气通过容器壁和外界进行热交换，温度逐步回升至室温T 0，达到状态IV(P 3 ，T 0 )，这是一个等容吸热过程。

O (P 0 ，T 0 ) ① 绝热压缩→ Ⅰ(P 1 ，T 1 )② 等容放热→ Ⅱ(P 2 ，T 0 )③ 绝热膨胀→ Ⅲ(P 0 ，T 2 )④ 等容吸热→ IV(P 3 ，T 0 )其中过程①、② 对测量γ没有直接影响，这两个过程的目的是获取温度等于环境温度T 0的压缩空气，同时可以观察气体在绝热压缩过程及等容放热过程中的状态变化。

对测量结果有直接影响的是③、④两个过程。

空气比热容空气的比热容没有确定值，即便是在温度确定时，通常使用定压比热容或定容比热容来反映空气比热容的大小，这两者都与温度有关（温差不太大时可认为基本相等）。

一定质量的物质，在温度升高时，所吸收的热量与该物质的质量和升高的温度乘积之比，称做这种物质的比热容（比热），用符号c表示。

其国际单位制中的单位是焦耳每千克开尔文[J /(kg·K) ]或焦耳每千克每摄氏度[J /(kg·℃)]。

J是指焦耳，K是指热力学温标，即令1千克的物质的温度上升（或下降）1开尔文所需的能量。

【声速测量空气比热容比】在普通物理实验中，测定空气比热容比的常用方法有绝热膨胀法、振动法、EDA 方法等。

大学物理实验中的空气比热容比实验采用的大多是FD-NCD 型测定仪，这种装置是人工打气、放气和关闭气阀来实现空气的绝热膨胀等过程，从而测得空气比热容比γ。

此方法简单易操作，但放气后靠人耳听到没气流声时才关闭气阀，这种人工操作是容易引起误差的，因为不同的人听觉灵敏度不一样，反应速度也不一样。

再则玻璃瓶充气后有形变，瓶内会有水汽，封口老化漏气等问题，这些在实验中都没有考虑。

若通过测量声速来测空气比热容比，可避免这一系列问题。

超声法是利用在理想气体中声波的传播过程可以认为是一个绝热过程，通过测定声速的方法来计算结果。

声速测量实验方法全为仪器操作，避免了FD-NCD 型空气比热容比测定仪实验中的人为因素的影响。

声速测量方法测得的空气比热容比误差比用FD-NCD 型空气比热容比测定仪测得的误差小，精度高。

在声速测量实验方法中采用双踪显示能直观显示两声波波形大小及相位关系。

【振动法测量空气比热容比】原理是通过实现热力学中的准静态过程（等温、等容及绝热），小钢球以小孔为中心上下作简谐振动，测定振动周期来计算结果。

振动法原理简明，装置简单，易操作，有其它方法无法比拟的优点。

空气的比热容比
空气的比热容比是一个用于描述空气的热容量或热导性的重要参数，其值会随着温度和压力的变化而变化。

在温度和压力恒定的条件下，空气的比热容比可以用下式计算：γ=cp/cv
其中，cp和cv分别代表定压比热容和定容比热容。

对于理想气体，比热容比是一个常数。

在标准状态下（273.15K，1大气压），空气的比热容比大约为1.40。

然而，由于空气不是理想的，它的比热容比会在不同温度和压力下有所变化。

在较高温度和较低压力下，空气的比热容比会略有增加。

空气比热容比的测定【实验目的】1.学习用绝热膨胀法测定空气的比热容比；2.观测热力学过程中状态变化及基本物理规律。

【实验仪器】活塞, 储气瓶一套，传感器，测空气压强的三位半数字电压表，测空气温度的四位半数字电压表，连接电缆及电阻【实验原理】实验开始时，首先关闭活塞C2。

打开活塞C1，由压气泡将原处于环境大气压强Ｐ。

室温0θ的空气压入贮气瓶Ｂ内，这时瓶内压强增大，温度变至一定值时，关闭活塞C1。

待稳定后，瓶内空气达到状态),,(111V P θI ，1V 为贮气瓶容积。

然后突然打开活塞C2，使瓶内空气与大气相通，到达状态),,(210V P θII 时迅速关闭活塞C2，由于放气过程很短，故认为此过程是一个近似的绝热过程。

瓶内气体压强减小，温度降低，绝热膨胀过程应该满足泊松定律：γγθϑ⎪⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛-10101P P (1) 由气态方程可知120011θθV P V P =（2）由以上两式子可以得到γγ2011V P V P = （3）当关闭活塞C2之后，贮气瓶内气体温度将升高，当升高到0θ时，到达状态),,(102V P θIII 。

从状态到I 状II 气体的体积不变。

由查理定律102θθ=P P （4） 由 (2)和(4)两式得2211V P V P = （5）再由（3）和（4）两式得()()1210log log log log P P P P --=γ （6）那么利用 （5）式这一测量公式，通过测量0P ，1P ，2P 的值可测量出空气的比热容γ的值。

【实验内容与步骤】1.连结好仪器，注意AD590的正负极不要接错，用Forton 式气压计测定大气压强p0，用水银温度计测定环境温度。

2.打开电源，将仪器预热20分钟，然后用调零电位器调节零点，把三位半数字电压表示值调到0.3．把活塞C2关闭，活塞C1打开。

用打气球把空气稳定地徐徐地压入气瓶B 中，用压力传感器和AD590温度传感器测量空气的压强和温度，记录瓶内压强均匀稳定时压强pI 和温度T0，由于仪器只显示大于大气压的部分，所以P1=P0+PI4．突然打开活塞C2，当气瓶的空气压强降低至环境大气压强P 0时（即放气声消失），迅速关闭活塞C2。

测定空气的比热容比实验补充内容(振动法)要求：用绝热膨胀法（见教材）和振动法两种方法．．．．测定空气的比热容比实验目的：1．理解热力学过程中状态变化及基本物理规律；2. 学会用振动法测定空气的比热容比。

实验原理：基本原理如图1所示：图1 实验基本原理气体的定压比热容p c 与定容比热容v c 之比v p c c /=γ 在热力学过程特别是绝热过程中是一个很重要的参数，测定的方法有好多种，这里介绍一种较新颖的方法，测定物体在特定容器中的振动周期来计算值。

振动物体小钢球A 的直径比玻璃管B 的直径仅小0.01-0.02mm ，所以它能在此精密的玻璃管中上下移动，在瓶子的壁上有一小口C ，并插入一根细管，通过它各种气体可以注入到烧瓶中。

为了补偿由于空气阻尼引起振动物体A 振幅的衰减，因此通过C 管一直注入一个小气压的气流。

在精密玻璃管B 中的中央开设有一个小孔。

当振动物体A 处于小孔下方的半个振动周期时，注入气体使容器内压力增大，引起物体A 上下振动，而当物体A 处于小孔上方的半个周期时，容器内的气体将通过小孔流出，使物体下沉，以后重复上述过程。

只要适当控制注入气体的流量，物体A 能在玻璃管B 的小孔上下作简谐振动。

设钢球A 的质量为m ，半径为r （直径为d ），当瓶子内压力P 满足下面条件时，刚球A 处于力平衡状态，2r mgp p l π+=式中l p 为大气压力。

若物体偏离平衡位置一个较小距离x ，则容器内的压力变化dp 物体的运动方程为： dp r dldx m 222π= （1） 因为物体振动过程相当快，所以可以看作绝热过程，绝热方程γpV =常数 （2）将（２）式求导数得出 Vdv p dp γ-=2r dV π= （3）将（３）代入（２）式得 ： 04222=⋅+x mV p r dtx d γπ 此式即为熟知得简谐振动方程，它得解为 ：T mV p r πγπω242== 即： 464Tpd mV =γ 式中各量均可方便测得，因而可算出γ值。