五年级下册数学解方程知识讲解

小学五年级下册数学《解方程》教案一、教学目标1.让学生理解方程的意义，掌握解方程的基本方法。

2.培养学生解决问题的能力，提高学生的思维品质。

二、教学重难点1.重点：理解方程的意义，掌握解方程的基本方法。

2.难点：灵活运用解方程的方法解决实际问题。

三、教学过程1.导入新课同学们，你们听说过方程吗？那你们知道方程是什么吗？对，方程就是含有未知数的等式。

今天我们就来学习解方程。

2.基本概念讲解我们要明确方程的定义。

方程是含有未知数的等式，例如：2x+3=7。

我们要学习解方程。

解方程就是找出使方程成立的未知数的值。

3.解方程方法讲解方法一：等式两边同时加减例如：2x+3=7，我们可以将等式两边同时减去3，得到2x=4，然后除以2，得到x=2。

方法二：等式两边同时乘除例如：3x=12，我们可以将等式两边同时除以3，得到x=4。

4.练习巩固现在我们来做一些练习题，巩固一下我们刚才学到的知识。

练习题：解下列方程（1）5x2=3（2）4x+7=19（3）6x÷3=45.实际问题应用下面我们来解决一些实际问题，看看如何运用解方程的方法。

例子：小明的年龄是哥哥的2倍，哥哥比小明大3岁。

求小明的年龄。

解：设小明的年龄为x岁，则哥哥的年龄为2x岁。

根据题意，我们有方程2xx=3。

解这个方程，得到x=3。

所以，小明的年龄是3岁。

同学们，今天我们学习了方程的定义和解方程的方法。

通过练习，我们知道了如何运用这些方法解决实际问题。

在以后的学习中，我们要学会灵活运用所学知识，不断提高自己的思维能力。

四、课后作业1.请同学们完成课后练习题，巩固解方程的方法。

2.家长签字确认。

五、教学反思本节课通过讲解方程的定义和解方程的方法，让学生掌握了基本的解方程技巧，并通过实际问题引导学生运用所学知识。

在教学过程中，要注意关注学生的学习反馈，及时调整教学方法和节奏，确保每个学生都能跟上教学进度。

同时，要注重培养学生的思维能力，鼓励他们积极思考，提高解决问题的能力。

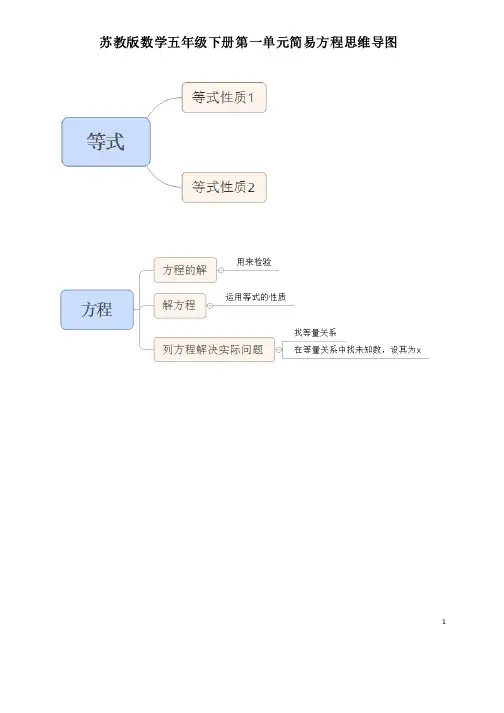
1 苏教版数学五年级下册第一单元简易方程思维导图等式和方程的含义等式和方程的含义等式：表示两个数（量）相等关系的式子。

比如3=3，3+4=7，3a+4a=7a ，4x+5=25，x 2=36方程：含有未知数的的等式叫做方程。

比如4x+5=25，x 2=36。

等式和方程之间的关系：等式不一定是方程，方程一定是等式。

练习一、算一算一、算一算5x+7x 8x+3x+12x 9x-5x 32x-19x-8x4(x+1)+3x 3(2x-3)+5(x+1)6x-(2x-3) 40-(30-5x)小结：化简代数式，也叫做合并同类项，同类的合并，不同类的不能合并。

小结：化简代数式，也叫做合并同类项，同类的合并，不同类的不能合并。

二、填空二、填空1.1. 下面的式子中，是等式的在后面（下面的式子中，是等式的在后面（ ）里画“√”。

）里画“√”。

X+18=36 X+18=36 （（ ）） x+2 x+2﹥﹥10 10 （（ ）） 72-x 72-x （（ ）） x=3 x=3 （（ ）） 3+4=7 3+4=7 （（ ）） 2.2. 下面的式子中，是方程的在后面（下面的式子中，是方程的在后面（ ）里画“√”。

）里画“√”。

X+18=36 X+18=36 （（ ）） x+2 x+2﹥﹥10 10 （（ ）） 72-x 72-x （（ ）） x=3 x=3 （（ ）） 3+4=7 3+4=7 （（ ）） 3.3. 在这一些式子①在这一些式子①5.25.25.2＋＋x=9.8x=9.8，②，②，②4.54.54.5－－4=0.54=0.5，③，③，③5x 5x 5x＜＜9.29.2，④，④，④x x ÷1.61.6，⑤，⑤，⑤4.24.24.2÷÷3=1.43=1.4，⑥，⑥，⑥7x 7x 7x÷÷7＞1.11.1，，⑦5x=1005x=100，，⑧7＋m －n=15中，等式有（ ）），方程有（ ））。

数学五年级下册用方程解决问题知识点1、简易方程：方程ax±b=c(a,b,c是常数)叫做简易方程。

2、方程：含有未知数的等式叫做方程。

(注意方程是等式，又含有未知数，两者缺一不可)方程和算术式不同。

算术式是一个式子，它由运算符号和已知数组成，它表示未知数。

方程是一个等式，在方程里的未知数可以参加运算，并且只有当未知数为特定的数值时，方程才成立。

3、方程的解使方程左右两边相等的未知数的值，叫做方程的解。

如果两个方程的解相同，那么这两个方程叫做同解方程。

4、方程的同解原理：(1)方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。

(2)方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程。

5、解方程：解方程，求方程的解的过程叫做解方程。

6、列方程解应用题的意义：用方程式去解答应用题求得应用题的未知量的方法。

7、列方程解答应用题的步骤(1)弄清题意，确定未知数并用x表示;(2)找出题中的数量之间的相等关系;(3)列方程，解方程;(4)检查或验算，写出答案。

8、列方程解应用题的方法(1)综合法先把应用题中已知数(量)和所设未知数(量)列成有关的代数式，再找出它们之间的等量关系，进而列出方程。

这是从部分到整体的一种思维过程，其思考方向是从已知到未知。

(2)分析法先找出等量关系，再根据具体建立等量关系的需要，把应用题中已知数(量)和所设的未知数(量)列成有关的代数式进而列出方程。

这是从整体到部分的一种思维过程，其思考方向是从未知到已知。

9、列方程解应用题的范围：小学范围内常用方程解的应用题：(1)一般应用题；(2)和倍、差倍问题；(3)几何形体的周长、面积、体积计算；(4)分数、百分数应用题；(5)比和比例应用题。

列方程解应用题练习1、共有1428个网球，每5个装一筒，装完后还剩3个，一共装了多少筒？2、故宫的面积是72万平方米，比天安门广场面积的2倍少16万平方米。

天安门广场的面积多少万平方米？3、宁夏的同心县是一个“干渴”的地区，年平均蒸发量是2325mm，比年平均降水量的8倍还多109mm，同心县的年平均降水量多少毫米？4、猎豹是世界上跑得最快的动物，能达到每小时110km，比大象的2倍还多30km。

五年级数学下册解方程一、方程的基本概念。

1. 方程的定义。

- 含有未知数的等式叫做方程。

例如：2x + 3 = 9，这里x是未知数，整个式子是一个等式，所以它是方程。

2. 方程的解。

- 使方程左右两边相等的未知数的值，叫做方程的解。

在方程2x+3 = 9中，x = 3时，方程左边=2×3 + 3=6 + 3=9，方程右边也是9，所以x = 3就是这个方程的解。

3. 解方程。

- 求方程的解的过程叫做解方程。

二、等式的性质（解方程的依据）1. 等式性质1。

- 等式两边加上或减去同一个数，左右两边仍然相等。

- 例如：如果a=b，那么a + c=b + c，a - c=b - c。

- 在解方程x+5 = 12时，根据等式性质1，方程两边同时减去5，得到x+5 - 5=12 - 5，即x = 7。

2. 等式性质2。

- 等式两边乘同一个数，或除以同一个不为0的数，左右两边仍然相等。

- 即如果a = b，那么ac=bc；如果a = b且c≠0，那么a÷c=b÷c。

- 例如，解方程3x = 18，根据等式性质2，方程两边同时除以3，得到3x÷3 = 18÷3，即x = 6。

三、解方程的步骤（以简单的一元一次方程为例）1. 移项。

- 把含未知数的项移到方程左边，常数项移到方程右边。

移项要变号。

- 例如：解方程2x+3 = 5x - 6。

- 首先将5x移到左边变为-5x，3移到右边变为-3，得到2x - 5x=-6 - 3。

2. 合并同类项。

- 对移项后的方程进行同类项合并。

- 在2x - 5x=-6 - 3中，2x-5x=-3x，-6 - 3=-9，方程变为-3x=-9。

3. 求解未知数。

- 根据等式性质，求出未知数的值。

- 在-3x=-9中，根据等式性质2，方程两边同时除以-3，得到x = 3。

四、常见的方程类型及解法。

1. ax + b=c型（a、b、c为常数，a≠0）- 例如：解方程3x+5 = 14。

小学五年级数学下册解方程的方法与技巧题目：小学五年级数学下册解方程的方法与技巧解方程是数学学习中的重要内容，小学五年级下册我们将学习解一元一次方程的方法与技巧。

本文将介绍三种常见的解方程方法：试算法、倒推法和平衡法，并给出实例进行详细说明。

一、试算法试算法是解方程的基本方法之一，适用于简单的一元一次方程。

通过尝试不同的数值来寻找满足等式的解。

例如，我们来解方程3x + 7 = 22：首先，我们尝试令x = 1，计算出等式左边的结果为3*1 + 7 = 10，并不满足等式。

接下来，我们尝试令x = 5，计算出等式左边的结果为3*5 + 7 = 22，等式成立。

因此，x = 5是方程3x + 7 = 22的解。

试算法的优点是简单易懂，适用于小学生解简单方程，但对于复杂的方程则不太适用。

二、倒推法倒推法是解一元一次方程的常用方法之一，适用于较复杂的方程。

通过逆向思维，从等式右边开始，逐步推导出满足等式的解。

例如，我们来解方程5x - 3 = 22：首先，我们将等式右边的22加上3，得到25。

然后，我们将25除以5，得到x = 5。

因此，x = 5是方程5x - 3 = 22的解。

倒推法的优点是适用范围广，可以解决一些复杂的方程，但要求学生对基本的数学运算熟练掌握。

三、平衡法平衡法是解一元一次方程的常用方法之一，适用于变量系数较大的方程。

通过保持等式两边的平衡，逐步求解出未知数。

例如，我们来解方程2x + 3 = 7x - 5：首先，我们将等式中的变量项移到等号的同一边，常数项移到等号的另一边。

得到2x - 7x = -5 - 3，化简为-5x = -8。

接下来，我们将等式两边同时除以-5，得到x = 8/5。

因此，x = 8/5是方程2x + 3 = 7x - 5的解。

平衡法的优点是适用于变量系数较大的方程，能够提高解题的效率。

综上所述，小学五年级下册数学教材中我们学习了解一元一次方程的三种常见方法：试算法、倒推法和平衡法。

人教版五年级数学解方程课程讲解一、引言在五年级的数学课程中，解方程是一个重要的内容。

通过解方程，学生可以培养逻辑思维能力，提高解决问题的能力。

本文将对人教版五年级数学解方程课程进行全面评估，并提供深度和广度兼具的讲解。

二、基本概念1. 解方程概念在数学中，方程是用等号连接的含有未知数的数学式。

而解方程，就是找出未知数的值使得等式成立的过程。

在五年级的数学课程中，通常会涉及一元一次方程的解法，学生需要通过运算找出未知数的值。

2. 解方程的意义解方程不仅是对数学知识的运用，更是对问题的思考和解决能力的培养。

通过解方程，学生可以培养逻辑推理和问题解决的能力，提高数学应用的技能。

解方程是数学课程中非常重要的一环。

三、课程内容讲解1. 一元一次方程在五年级的数学课程中，一元一次方程是最基本的内容之一。

一元一次方程是指方程中只含有一个未知数，并且该未知数的最高次数为1。

学生在解一元一次方程时，通常会使用加减乘除的基本运算法则，逐步找出未知数的值。

2. 解方程的步骤解一元一次方程通常有一定的步骤。

首先是观察方程中的运算符号和未知数的位置，然后根据方程的特点选择适当的运算法则，逐步化简方程，最终得出未知数的值。

学生在学习解方程时，需要理解并掌握这些基本步骤。

3. 实际问题的应用解方程并不局限于抽象的数学式，实际问题中也会涉及到解方程的运用。

在课程中，老师通常会引导学生通过实际问题来理解解方程的意义和运用方法。

通过一些生活中的例子，帮助学生理解解方程在实际问题中的应用。

四、个人观点和理解解方程是数学课程中非常重要的内容，它不仅能够培养学生的逻辑思维能力，还可以提高他们解决问题的能力。

在教学过程中，我认为老师应该注重培养学生的思维能力，引导他们通过解方程来思考和解决实际问题，而不仅仅是停留在计算的层面。

五、总结通过本文的讲解，相信读者对人教版五年级数学解方程课程有了更清晰的了解。

解方程是数学课程中的重要内容，学生需要通过实际的练习来掌握解方程的方法和技巧。

五年级下册解方程分数是一个重要的数学概念，它涉及到如何将分数应用于等式中并解决实际问题。

以下是一些基本步骤和示例，以帮助您理解如何解决这种问题。

示例 1: 简单的分数方程
1. 假设我们有一个分数方程：3/4 = x/5。

2. 我们首先找出公分母，这里是4和5。

3. 将方程两边都乘以这个公分母：3×5/4×5 =
x×4/5×4。

4. 化简方程，得到：15/20 = 4x/20。

5. 进一步化简，得到：x = 15/4。

示例 2: 更复杂的分数方程
1. 假设我们有一个更复杂的分数方程：(3x + 2)/4 = (5x - 1)/6。

2. 我们首先找出公分母，这里是4和6。

3. 将方程两边都乘以这个公分母：(3x + 2)×6/4×6 = (5x - 1)×4/6×4。

4. 化简方程，得到：18x + 12/24 = 20x - 4/24。

5. 将所有项移到等式的一侧，然后解方程：18x - 20x = -12/4 - (-12/4)。

6. 解得：x = 1。

通过这些示例，您可以看到解分数方程的基本步骤是：
1. 找出公分母。

2. 将方程两边都乘以这个公分母，以消除分数。

3. 化简方程，直到找到解。

这些步骤在五年级下册的数学课程中是非常重要的，因为它们为学生提供了解决更复杂数学问题的工具和技能。

通过反复练习，学生将能够熟练掌握解分数方程的技巧。

一、方程的概念1.方程的含义：方程是一个等式，它包含有一个未知数，表示未知数的值满足等式。

2.方程的组成：方程由等号连接两个代数式组成，其中一个代数式称为等式的左边，另一个代数式称为等式的右边。

3.方程的表示方法：一般使用字母表示未知数，常用的表示方式为"未知数+运算符+已知数=目标数"，例如：x+3=7二、解方程的方法1.倒退法：通过逐步倒退等式中的计算步骤，得到未知数的值。

例如：x+2=7，先减去2得到x=52.等式两边相等法：利用等式两边相等的性质，对等式进行运算，得到未知数的值。

例如：3+y=8，先减去3得到y=53.等式移项法：通过移项操作将同类项移到等式的一边，得到未知数的值。

例如：4x+5=9，先减去5再除以4得到x=1三、方程的应用1.运用方程解决实际问题：例如，一些数加上5等于8，可以用方程x+5=8表示，通过解方程得到x的值为3，即这个数是32.列方程建立数学模型：通过列方程建立数学模型，解决实际问题。

例如，一些数减去3等于8，可以用方程x-3=8表示，通过解方程得到x的值为11，即这个数是113.化解合并与分割问题：通过方程来化解合并与分割问题，求出合并前或者分割后每个部分的值。

例如，把一个数4等分，每一份是3，可以用方程3x=12表示，通过解方程得到x的值为4，即原来的数是12四、方程的常见错误1.忽略了方程中的运算：对于一个方程，必须进行正确的运算操作，不能忽略等号两边的计算步骤。

2.未知数读错或写错：在列方程或解方程时，要仔细确认未知数的字母表示，避免读写错误。

3.不正确使用运算法则：在解方程时，要正确运用运算法则，尤其是正负号的运算，避免计算错误。

4.引入新的未知数：解方程时，要及时记录求解的未知数，避免引入新的未知数，导致解题错误。

五年级数学方程知识点就介绍到这里，方程是数学中重要的概念和方法，通过学习方程的相关知识，可以提高解决实际问题的能力，培养逻辑思维和数学思维。

小学五年级数学解方程口诀及知识点汇总（附习题）
解方程口诀、知识点
解方程一直是小学数学的重难点，类型多且容易混淆，如何快速有效的让学生掌解方程，通过总结分析，我汇总了各类方程的解决的技巧，编纂了一首口诀帮助记忆：
一般方程很简单，
具体数字帮你办，
加减乘除要相反。

特殊方程别犯难，
减去除以未知数，
加上乘上变一般。

若遇稍微复杂点，
舍远取近便了然。

具体分析如下：
我们可以把课本中出现的方程分为三大类：一般方程，特殊方程，稍复杂的方程。

形如：x+a=b , x-a=b , ax=b , x÷a=b 这几种方程，我们可以称为一般方程。

形如：a- x =b，a÷x =b这两种方程，我们可以称为特殊方程。

形如：ax+b=c , a（x-b）=c这两种方程，我们可以称为稍复杂的方程。

我们知道，对于一般方程，如果方程是加上a，在利用等式的性质求解时，会在方程的两边减去a，同样，如果方程是减去a，在利用等式的性质求解时，会在方程的两边加上a，乘和除以也是一样的，换句话说，加减乘除是相反的，并且加减乘除的都是一个具体的数字。

总结一句话就是：一般方程很简单，具体数字帮你办，加减乘除要相反。