五年级下册数学解方程76996知识讲解

小学五年级数学简易方程的知识点归纳人教版小学五年级数学简易方程的知识点归纳在日常的学习中，说到知识点，大家是不是都习惯性的重视？知识点就是“让别人看完能理解”或者“通过练习我能掌握”的内容。

你知道哪些知识点是真正对我们有帮助的吗？下面是店铺为大家收集的人教版小学五年级数学简易方程的知识点归纳，希望能够帮助到大家。

小学五年级数学简易方程的知识点归纳篇1方程ax±（×÷b）=c（a,b,c是常数）叫做简易方程。

1、方程的意义含有未知数的等式，叫做方程。

2、方程和等式的关系3、方程的解和解方程的区别使方程左右两边相等的未知数的值，叫做方程的解。

求方程的解的过程叫做解方程。

4、列方程解应用题的一般步骤(1)弄清题意，找出未知数，并用表示。

(2)找出应用题中数量之间的相等关系，列方程。

(3)解方程。

(4)检验，写出答案。

5、数量关系式加数=和-另一个加数减数=被减数–差被减数=差+减数因数=积另一个因数除数=被除数商被除数=商除数例4用含有字母的式子表示下面的数量关系(1)的7倍;(2)的5倍加上6;(3)5减的差除以3;(4)200减5个;(5)比7个多2的数。

例9要修一段公路，平均每天修米，修了6天，还剩下米。

(1)用含有字母的式子表示这段公路有多少米;(2)根据这个式子，分别求等于50，等于200时，公路长多少米例11某个数与9的和的12倍等于156，求这个数是多少。

例12王晰买了2支钢笔和5支圆珠笔，共付17元。

一支钢笔的价格是一支圆珠笔的40倍，求每支钢笔多少钱，每支圆珠笔多少钱? 小学五年级数学简易方程的知识点归纳篇21、用字母表运算定律。

加法交换律： a+b=b+a 加法结合律： a+b+c=a+(b+c)乘法交换律：a×b=b×a 乘法结合律：a×b×c=a×(b×c)乘法分配律：(a±b)×c=a×c±b×c2、用字母表示计算公式。

第一讲方程（一）、确定位置【知识要点】一、1、等式与方程； 2、等式的性质。

3、解方程； 4、列方程解应用题。

二、1、表示相等关系的式子叫做等式。

2、含有未知数的等式是方程。

3、方程一定是等式；等式不一定是方程。

等式>方程4、等式两边同时加上或减去同一个数，所得结果仍然是等式。

这是等式的性质。

等式两边同时乘或除以同一个不等于0的数，所得结果仍然是等式。

这也是等式的性质。

5、求方程中未知数的过程，叫做解方程。

解方程时常用的关系式：一个加数＝和－另一个加数减数＝被减数－差被减数＝减数＋差一个因数＝积÷另一个因数除数＝被除数÷商被除数＝商×除数注意：解完方程，要养成检验的好习惯。

6、五个连续的自然数（或连续的奇数，连续的偶数）的和，等于中间的一个数的5倍。

奇数个连续的自然数（或连续的奇数，连续的偶数）的和÷个数=中间数7、4个连续的自然数（或连续的奇数，连续的偶数）的和，等于中间两个数或首尾两个数的和×个数÷2（高斯求和公式）8、列方程解应用题的思路：A、审题并弄懂题目的已知条件和所求问题。

B、理清题目的等量关系。

C、设未知数，一般是把所求的数用X表示。

D、根据等量关系列出方程E、解方程F、检验G、作答。

【经典例题】知识点：等式：表示相等关系的式子叫做等式。

练习：1、下面的式子中，是等式的在后面（）里画“√”。

X+18=36 （） x+2﹥10 （） 72-x （） x=3 （）知识点：方程：含有未知数的等式是方程。

练习：1、下面的式子中，是方程的在后面（）里画“√”。

X+18=36 （） x+2﹥10 （） 72-x （） x=3 （）知识点：方程与等式的关系：方程一定是等式，等式不一定是方程。

练习：1、哪些是等式，哪些是方程，请填入相应的横线上。

(填序号)①3+x=12 ② 3.6+x ③ 4+17.5=21.5 ④48+x﹤63等式________________________；方程：________________________2、含有未知数的式子叫方程。

解简易方程之方法及难点归纳重点概念：方程，方程的解，解方程，等式的基本性质（详见“知识点汇总”）要点回顾：“解方程”就是要运用“等式的基本性质”，对“方程”的左右两边同时进行运算，以求出“方程的解”的过程。

（方程的解即是如同“X＝6”的形式）“解方程”就好像是要把复杂的绳结解开，因此一般要按照“绳结”形成的过程逆向操作（逆运算）。

过程规范：先写“解：”，“＝”号对齐往下写，同时运算前左右两边要照抄，解的未知数写在左边。

注意事项：以下内容除了标明的外，全都是正确的方程习题示例，且没有跳步，请仔细观看其中每步的解题意图。

带“*”号的题目不会考查，但了解它们有助于掌握解复杂方程的一般方法，对简单的方程也就自然游刃有余了。

一、一步方程只有一步计算的方程，直接逆运算除未知数外的部分。

难点：当未知数出现在减数和除数时，要先逆运算含未知数的部分。

二、两步方程两步方程中，若是只有同级运算，也可以先计算，后当做一步方程求解。

注意要“带符号移动”，增添括号时还要注意符号的变化。

如果含有两级运算，就“逆着运算顺序”同时变化，如含有未知数的一边是“先乘后减”，则先逆运算减法（即两边同加），再逆运算乘法（即两边同时除以），依此类推。

难点：当未知数出现在减数和除数时，要先把含有未知数的部分看作一个整体（可以看成是一个新的未知数），就相当于简化成了一步方程。

因此原方程就可以看成是6＋y＝10，5y＝6和10－y＝8的形式。

三、三步方程（一）应用乘法分配律，共同因数是已知数的具有乘法分配律的形式，即两个有共同因数的乘积（或具有相同除数的除法式子）相加或相减，而共同因数（或除数）是已知数的，既可以逆用乘法分配律提取共同因数而将其简化为两步方程，也可以直接算出已知部分而化简。

通过比较可以看出，一般来说提取共同因数的方法确实计算量要少一些，不容易算错。

（二）应用乘法分配律，共同因数是未知数的具有乘法分配律的形式，即两个有共同因数的乘积（或具有相同除数的除法式子）相加或相减，而共同因数（或除数）是未知数的，只能逆用乘法分配律提取共同因数而将其难点：隐藏的因数或错看的未知数容易成为此类问题的难点和易错点。

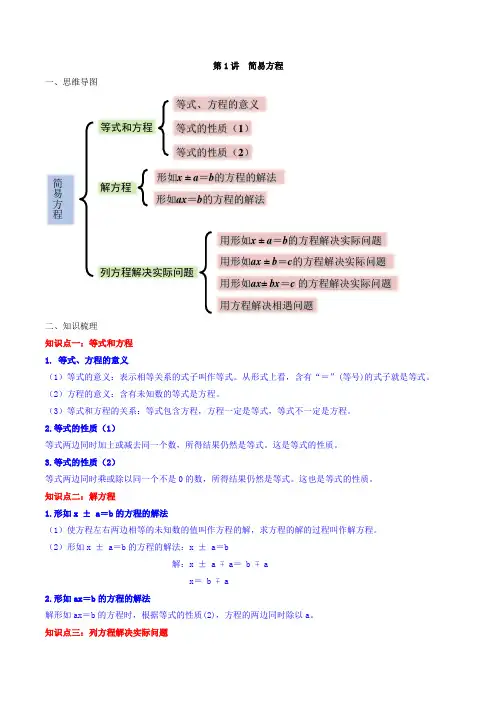
第1讲简易方程一、思维导图简易方程等式、方程的意义等式的性质（1）形如x ±a ＝b 的方程的解法等式的性质（2）列方程解决实际问题形如ax ＝b 的方程的解法解方程用形如ax ±bx ＝c 的方程解决实际问题等式和方程用形如x ±a ＝b 的方程解决实际问题用形如ax ±b ＝c 的方程解决实际问题用方程解决相遇问题二、知识梳理知识点一：等式和方程1. 等式、方程的意义（1）等式的意义：表示相等关系的式子叫作等式。

从形式上看，含有“＝”(等号)的式子就是等式。

（2）方程的意义：含有未知数的等式是方程。

（3）等式和方程的关系：等式包含方程，方程一定是等式，等式不一定是方程。

2.等式的性质（1）等式两边同时加上或减去同一个数，所得结果仍然是等式。

这是等式的性质。

3.等式的性质（2）等式两边同时乘或除以同一个不是0的数，所得结果仍然是等式。

这也是等式的性质。

知识点二：解方程1.形如x ± a＝b的方程的解法（1）使方程左右两边相等的未知数的值叫作方程的解，求方程的解的过程叫作解方程。

（2）形如x ± a＝b的方程的解法：x ± a＝b解：x ± a ∓ a＝ b ∓ ax＝ b ∓ a2.形如ax＝b的方程的解法解形如ax＝b的方程时，根据等式的性质(2)，方程的两边同时除以a。

知识点三：列方程解决实际问题1.用形如x ± a＝b的方程解决实际问题列方程解决问题的具体步骤：(1)写解和设句；(2)根据相等关系列方程；(3)解方程；(4)检验；(5)写出答语。

2.用形如ax ± b＝c的方程解决实际问题（1）相等关系：已知数量甲比乙的几倍多(或少)几和数量甲，求数量乙的实际问题，可设数量乙为x，根据数量乙×倍数±几＝数量甲，列出形如ax ± b＝c的方程进行解答。

（2）形如ax± b＝c的方程的解法：ax ±b＝c解：ax ±b ∓ b＝ c∓ b ax＝ c∓ b x＝ (c ∓ b)÷a3.用形如ax± bx＝c 的方程解决实际问题（1）解决涉及两个未知量的问题时，一般设标准量为x，另一个未知量用含有x的式子表示，然后根据等量关系式列方程求解。

北师大版五年级数学下册知识点详解及练习第七单元用方程解决问题北师大版五年级数学下册知识点详解及练习第七单元用方程解决问题 (1)7.1 邮票的张数（解ax ±x=b 的方程） (1)知识点1：ax ±bx=c 类型方程的应用 (1)7.2 相遇问题（运用方程解决实际问题） (2)知识点1：列方程解应用题步骤： (2)知识点2：相遇问题的解法 (3)第七单元用方程解决问题7.1 邮票的张数（解ax ±x=b 的方程）知识点1：ax ±bx=c 类型方程的应用解“ax±bx=c （a ≠0）”形式的方程，先将其转化成“（a±b ）x=c ”的形式，再求出未知数x 的值。

在列方程解答应用题时，遇到题中有两个未知数时，可以将一个未知数设为x ，再根据两个未知数之间的关系，用含字母的式子表示另一个未知数。

【练习1】解方程1÷2x = －2110x = 145 56x ÷73 = 37x －85x = 15 x ÷76×149 = 43 X+35=84Y-27=38 7X-40=540 3X+8=5325-0.8X=17 12.8÷X=0.8【练习2】列方程计算。

（１）一个数与45的和是87，这个数是多少？（２）有一个数，它是27的8倍，这个数是多少？（3）一个长方形的周长是24米，宽是4米，长是多少米？（4）学校体育组买足球花了240元，比买篮球花的钱数的三倍少84元，买篮球花了多少钱？（5）建筑工地上有两堆砖，第一堆的块数是第二堆的1.2倍，如果再给第二堆增加3600块，两堆的块数就相等了。

两堆砖原来各有多少块？【练习3】自我挑战。

◎+☆+☆+☆=70 △+△+▲+▲+▲=17◎+☆=50 △+▲=7◎=（）☆=（）△=（）▲=（）7.2 相遇问题（运用方程解决实际问题）知识点1：列方程解应用题步骤：（1）找到题中的等量关系式；（2）设所求量为x（3）根据等量关系式列出相应的方程；（4）解答方程，注意结果无单位名称；（5）检验作答。

小学五年级数学下册学会解方程解方程是数学中的重要内容之一，在小学五年级的数学学习中，解方程也是一个重要的主题。

通过解方程，孩子们可以提高他们的逻辑思维能力和问题解决能力。

本文将介绍小学五年级数学下册学会解方程的方法和步骤。

一、什么是方程在学习解方程之前，我们首先要了解什么是方程。

方程是一个数学表达式，它表示两个量之间的关系。

方程中包含一个或多个未知数，我们的目标是找到使方程成立的未知数的值。

二、解一元一次方程1. 一元一次方程的定义一元一次方程是指只包含一个未知数和一次项的方程。

它的一般形式为ax + b = c，其中a、b、c为已知数，a≠0。

2. 解一元一次方程的步骤解一元一次方程的基本步骤如下：（1）将方程中的未知数和已知数分开，并将未知数的项移至方程的一边，已知数的项移至方程的另一边，使方程变为ax = b的形式。

（2）通过除以a的方式，将系数为a的项的系数化为1，即得到x = b/a。

（3）计算b/a的结果，即得到未知数x的值。

3. 解一元一次方程的例子举例说明解一元一次方程的步骤：题目：5x + 3 = 18（1）将未知数项5x移至方程的一边，已知数项3移至方程的另一边，得到5x = 18 - 3。

（2）将5x = 15化简为x = 15/5。

（3）计算15/5的结果，得到x = 3。

因此，方程5x + 3 = 18的解为x = 3。

三、解两步方程1. 两步方程的定义两步方程是指包含两个运算步骤的方程。

解决两步方程的关键是逆向运算，即将已知数的处理步骤逆转。

2. 解两步方程的步骤解两步方程的基本步骤如下：（1）将已知数项移至方程的一边，未知数项移至方程的另一边。

（2）根据运算逆向原则，对方程进行逆向运算，得到未知数的解。

3. 解两步方程的例子题目：2x + 5 = 9（1）将已知数项5移至方程的一边，未知数项2x移至方程的另一边，得到2x = 9 - 5。

（2）将2x = 4化简为x = 4/2。

一、字母表示数第 1 部分简易方程知识点梳理二、方程的定义及解方程1、方程：含有未知数的等式称为方程。

2、方程的解：使方程左右两边相等的未知数的值，叫做方程的解。

1、在含有字母的式子里，字母中间的乘号可以记作“·”，也可以省略不写。

加号、减号除号以及数与数之间的乘号不能省略。

3、解方程：求方程的解的过程叫做解方程。

4、解方程原理：天平平衡。

等式左右两边同时加、减、乘、除相同的数（0 除外），等式依然成立。

2、a ×a 可以写作a ·a(或a2) ，5、方程两边同时加、减、乘、除一个不等于 0 的数，左右两边仍然相等。

a2读作a 的平方，表示两个a 相乘。

2 a 表示a + a3、数字和字母相乘，省略乘号时要把数字写在前面。

（如 b×4 写作 4b ）对应练习1.排球队共有队员a 人，女队员有7 人，男队员有( )人。

2.1 千克大米的价钱是1.50 元，买x 千克大米应付( )元。

3.甲数比乙数的3 倍还多a，甲数是x，乙数是( )；如果乙数是x，那么甲数是( )。

4.省略乘号，写出下面的式子。

3×a9×x a×4y×5a×3x⒊方程0.6x=3 的解是（）。

⒋ac+bc=( □ + □ )×□⒌a与b 的和的5 倍是（）⒍梯形面积计算公式用字母表示是（），三角形面积计算公式用字母表示是（）。

⒎一个三角形的面积是 4.8 平方米，它的底边长是 1.2 米，高是 x 米，写出含有 x 的等量关系式是（）。

⒏当a=2,b=5 时，那么8a－2b=（）。

⒐正方形的边长为x 厘米，4x 表示（），x2表示（）。

10.有x 吨水泥，运走10 车，每车a 吨。

仓库还剩水泥（）吨。

6、解方程需要注意什么？（1）、一定要写‘解’字。

（2）、等号要对齐。

（3）、两边乘除相同数的时候，这个数不要为 07、10 个数量关系式：加法：和=加数+加数一个加数=和-另一个加数减法：差=被减数-减数被减数=差+减数减数=被减数-差乘法：积=因数×因数一个因数=积÷另一个因数除法：商=被除数÷除数被除数=商×除数除数=被除数÷商8、方程和等式的关系：含有未知数的等式叫做方程，所有的方程都是等式，但等式不一定都是方程。

小学五年级解方程的方法详解
1、方程：含有未知数的等式叫做方程。

如5x-3=22，4x-(2x-6)=20
2、方程的解：使方程成立的未知数的值叫做方程的解。

如上式解得x=5
3、解方程：求方程的解的过程叫做解方程。

4、解方程的依据：方程就是一架天平，“=”两边是平衡的，一样重！性质：（1）等式两边同时加或减一个相同的数，得到的结果仍然是等式；
（2）等式两边同时乘或除以一个相同的数（0不作除数），得到的结果仍然是等式。

5、解方程的步骤：
（1）去括号：（1）运用乘法分配律；（2）括号前边是“－”，去掉括号要变号；括号前边是“＋”，去掉括号不变号。

（2）移项：法1——运用等式性质，两边同加或同减，同乘或同除；
法2——符号过墙魔法，越过“=”时，加减号互变，乘除号互变。

注意两点：（1）总是移小的；（2）带未知数的放一边，常数值放另一边。

（3）合并同类项：未知数的系数合并；常数加减计算。

（4）系数化为1：利用同乘或同除，使未知数的系数化为1。

（5）写出解：未知数放在“=”左边，数值（即解）放右边；如x=5
（6）验算：将原方程中的未知数换成数，检查等号两边是否相等！注意：（1）做题开始要写“解：”（2）上下“=”要始终对齐。