【配套K12】七年级数学上册第6章图形的初步知识6.4线段的和差分层训练新版浙教版

最新教学资料·浙教版数学6.4 线段的和差1．如果一条线段的____________是另两条线段的____________的____________，那么这条线段就叫做另两条线段的和．2．如果一条线段的____________是另两条线段的____________的____________，那么这条线段叫做另两条线段的差．3．两条线段的和或差仍是一条____________．4．若点C把线段AB分成____________的两条线段AC与BC，则点C叫做线段AB的中点．A组基础训练1．如图，AD＝CB，则AC与BD的长度关系是( )A．AC>BD B．AC<BD C．AC＝BD D．不能确定第1题图2．如图，如果点C是线段AB的中点，那么①AB＝2AC；②2BC＝AB；③AC＝BC；④AC ＋BC＝AB，上述四个式子中，正确的有( )第2题图A．1个 B．2个 C．3个 D．4个3．如图，下列关系式中与图形不符合的是( )第3题图A．AD－CD＝AB＋BCB．AC－BC＝AD－BDC．AC－BC＝AC＋BDD ．AD －AC ＝BD －BC4．如图，有a ，b ，c 三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线中( )第4题图A ．a 户最长B ．b 户最长C ．c 户最长D ．一样长5．如图，C 是线段AB 上一点，M 是线段AC 的中点，若AB ＝8cm ，BC ＝2cm ，则MC 的长是( )第5题图A ．2cmB ．3cmC ．4cmD ．6cm6．已知线段AB ＝6，C 在线段AB 上，且AC ＝13AB ，点D 是AB 的中点，那么DC 等于( )A ．1B ．2C ．3D ．4 7．如图，直线上有四个点A ，B ，C ，D ，看图填空：第7题图(1)AC ＝____________＋BC ； (2)CD ＝AD －____________；(3)AC＋BD－BC＝____________.8．如图所示，M，N在线段AB上，且MB＝4cm，NB＝16cm，且点N是AM的中点，则AB ＝____________cm.第8题图9．如图所示，M，N把线段AB三等分，C为NB的中点，且CN＝5cm，AB＝____________cm.第9题图10．在一次实践操作中，小张把两根长为23cm的竹竿绑接成一根长40cm的竹竿，则重叠部分的长为____________cm.11．如图，已知线段a，b(a＞b)，画一条线段，使它等于2a－b.第11题图12．先画图，再计算．(1)画线段AB＝2cm，延长线段AB至点C，使AC＝2AB，取线段BC的中点D；(2)求线段BD的长．13．如图，A，B是线段MN上的两点，且MA∶AB∶BN＝2∶3∶4，MN＝36cm，求线段AB 和BN的长度．第13题图B组自主提高14．下列说法：①若PA＝PB，则P是线段AB的中点；②到线段两个端点距离相等的点必是线段的中点；③点A，B，C在同一直线上，且AC＝2，BC＝4，点P是AB的中点，则CP＝1.其中不正确的是____________(填序号)．15．已知线段AB＝12cm，点C是直线AB上一点，且AC∶BC＝1∶2，若D是AC的中点，求线段CD的长．C组综合运用16．(1)如图，点C在线段AB上，AC＝10cm，CB＝8cm，M，N分别是AC，BC的中点，求线段MN的长；第16题图(2)若C为线段AB上任一点，AC＋CB＝x(cm)，(1)中其他条件不变，你能猜想MN的长度吗？并说明理由．你能用一句简洁的话描述你发现的结论吗？(3)若点C在线段AB的延长线上，AC－BC＝y(cm)，M，N分别为AC，BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由；(4)把(1)条件中的”如图”去掉，”点C在线段AB上”改成”点C在直线AB上”，其余条件不变，你能得出线段MN的长度吗？参考答案6．4线段的和差【课堂笔记】1．长度长度和 2.长度长度差 3.线段 4.相等【分层训练】1．C 2.D 3.C4．D【解析】同一条电线中竖着的线段两两相加，可知每户的两条竖线加起来一样长；每户横着的线段也一样长．5．B 6.A 7．(1)AB (2)AC (3)AD 8．28 9.30 10.6 11．(1)作射线AP.(2)用圆规在射线AP上截取AB＝BC＝a.(3)用圆规在线段BC的反方向上截取CD＝b.线段AD就是所要作的线段，即AD＝2a－b(见图)．第11题图12．(1)如图：第12题图(2)BD＝1cm.13．设MA＝2x，则AB＝3x，BN＝4x，∴MN＝MA＋AB＋BN＝9x＝36，∴x＝4，∴AB＝3x ＝12cm，BN＝4x＝16cm.14．①②③15．根据题意，有两种情况：①当点C在线段AB上时，如图1.设AC＝x，则BC＝2x.∵AB＝12cm，∴AB＝AC＋BC＝x＋2x＝3x＝12，∴x＝4，∴AC＝4cm.又∵D是AC的中点，∴CD＝12AC＝2cm.②当点C在线段BA的延长线上时，如图2.第15题图∵AC＝BC ＝1∶2，∴A 为BC 的中点， ∴AC ＝AB ＝12cm .又∵D 为AC 的中点，∴CD ＝12AC ＝6cm .综上所述，CD 的长为2cm 或6cm .16．(1)MN ＝MC ＋CN ＝12AC ＋12CB ＝5＋4＝9(cm )．(2)MN ＝12x(cm )．理由：MN ＝MC ＋CN ＝12AC ＋12CB ＝12(AC ＋CB)＝12AB ＝12x(cm )．结论：若C 为线段AB 上任一点，M ，N 分别是AC ，BC 的中点，则线段MN 的长是线段AB 长的一半．(3)MN ＝12y(cm )．理由：如图，MN ＝MC －NC ＝12AC －12BC ＝12(AC －BC)＝12y(cm )．第16题图(4)1cm 或9cm .。

6.7 角的和差1．如果____________的度数是____________的度数的和，那么这个角就叫做另两个角的____________．2．如果____________的度数是____________的度数的____________，那么这个角就叫做另两个角的差．3．从一个角的____________引出的一条射线，把这个角分成两个____________的角，这条射线叫做这个角的角平分线．A 组 根底训练1．将一副直角三角尺按如下不同方式摆放，那么图中锐角α与β相等的是( )2．如图，点O 在直线AB 上，射线OC 平分∠DOB.假设∠COB ＝35°，那么∠AOD 等于( )第2题图A ．35°B ．70°C ．110°D ．145°3．用一副三角板画角时可画出许多不同度数的角，以下哪个度数画不出来( )A ．15°B ．75°C ．105°D ．65°4．(宁波中考)∠AOB ＝60°，在∠AOB 内取一点C ，引射线OC ，假设∠AOC 是∠BOC 的23，那么∠AOC 为( )A ．20°B ．24°C ．36°D ．40°5．∠AOB ＝60°，∠BOC ＝45°，那么∠AOC 为( )A ．105°B ．15°C ．105°或15°D ．75°6．根据图填空：(1)∠AOC ＝∠AOB ＋∠____________；(2)∠BOD ＝∠COD ＋∠____________；(3)∠AOC ＝∠AOD －∠____________；(4)∠BOC ＝∠____________－∠____________－∠DOC ；(5)∠BOC ＝∠AOC ＋∠BOD －∠____________.第6题图6．如图，将一副直角三角尺叠放在一起，使直角顶点重合于点C.假设∠ACD＝120°，那么∠BCE＝____________.第7题图8．(1)如图1，O是AB上一点，OE平分∠BOC，OF平分∠AOC，那么∠EOF的度数是____________．图1图2(2)如图2，O是AB上一点，∠BOC＝Rt∠，∠AOD∶∠BOD＝2∶7，那么∠COD的度数是____________．图3第8题图(3)如图3，∠AOD＝130°，∠AOC＝88°，OB是∠AOD的平分线，那么∠BOC的度数是____________．9．如图，∠AOC和∠BOD都是直角．第9题图(1)假设∠DOC＝25°，那么∠AOB的度数是____________；(2)假设∠AOB＝152°，那么∠DOC的度数是____________．10．(1)如图1，将长方形ABCD沿AE折叠，使点D落在点D′的位置．假设∠CED′＝60°，那么∠AED的度数是____________．图1图2第10题图(2)如图2，将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上，不与点B，C重合)，使点C落在长方形的内部点E处．假设FH平分∠BFE，那么∠GFH的度数是____________．11．如图，OB是∠AOC内部的一条射线，把三角尺的60°的顶点放在点O处，转动三角尺，当三角尺的OD边平分∠AOB时，三角尺的另一边OE也正好平分∠BOC.求∠AOC的度数．第11题图12．如图，∠BOC－∠BOA＝14°，∠BOC∶∠COD∶∠AOD＝2∶3∶4，求∠COD的度数．第12题图B 组 自主提高13．如图，∠BOD ＝2∠AOB ，OC 是∠AOD 的平分线，那么以下四个结论：①∠BOC ＝13∠AOB ；②∠COD ＝2∠BOC ；③∠BOC ＝12∠AOB ；④∠COD ＝3∠BOC.其中正确的选项是( ) 第13题图A ．①②B ．③④C ．②③D ．①④14．∠AOB ＝40°，过点O 引射线OC ，假设∠AOC∶∠COB ＝2∶3，且OD 平分∠AOB ，求∠COD 的度数．C 组 综合运用15．如图1是一副三角尺拼成的图案：(所涉及角度均小于或等于180度)(1)∠EBC 的度数为________度；(2)将图1中的三角尺ABC 绕点B 旋转α度(0°＜α＜90°)能否使∠EBC ＝2∠ABD ？假设能，那么求出α的值；假设不能，说明理由．(图2、图3供参考)第15题图参考答案6．7角的和差【课堂笔记】1．一个角另两个角和 2.一个角另两个角差 3.顶点相等【分层训练】1．B 2.C 3.D 4.B 5.C 6．(1)BOC (2)COB (3)DOC (4)AOD AOB (5)AOD 7．60°8．(1)90°(2)50°(3)23°9．(1)155°(2)28°10．(1)60°(2)90°11．∠AOC＝120°12．∠COD＝102°13．B14．有两种情况：(1)如图1所示，当射线OC在∠AOB的内部时，由∠AOC∶∠COB＝2∶3，可设∠AOC＝2x°，那么∠COB＝3x°.∵∠AOB＝40°，∴∠AOC＋∠COB＝40°.∴2x＋3x＝40，解得x＝8.∴∠AOC＝2x°＝16°.∵OD平分∠AOB，∴∠AOD＝12∠AOB＝12×40°＝20°.∴∠COD＝∠AOD－∠AOC＝20°－16°＝4°.第14题图(2)如图2所示，当射线OC在∠AOB的外部时，由∠AOC∶∠COB＝2∶3，可设∠AOC＝2x°，那么∠COB＝3x°.∵∠AOB＝40°，∴∠COB－∠AOC＝40°.∴3x－2x＝40，解得x＝40.∴∠AOC＝2x°＝80°.∵OD平分∠AOB，∴∠AOD＝12∠AOB＝12×40°＝20°.∴∠COD＝∠AOD＋∠AOC＝20°＋80°＝100°.综上所述，∠COD的度数为4°或100°.15．(1)∵∠EBD＝90°，∠ABC＝60°，∴∠EBC＝∠EBD＋∠ABC＝90°＋60°＝150°.故答案为：150.(2)能；①逆时针旋转：90°＋60°－α＝2α，解得：α＝50°；②顺时针旋转：当0°＜α＜30°时，有90°＋60°＋α＝2α，解得：α＝150°，不符题意，舍去；当30°＜α＜90°时，有360°－90°－60°－α＝2α，解得：α＝70°.综上所述，逆时针旋转α＝50°或顺时针旋转α＝70°.。

6.3 线段的长短比较1．一般地，如果两条线段____________，那么我们就说这两条线段相等．2．在所有连结两点的线中，____________最短，简单地说，____________.3．____________叫做这两点间的距离．A组基础训练1．下列说法正确的是( )A．直线可以比较长短B．直线比射线长C．线段可以比较长短D．线段可能比直线长2．已知线段AB和线段CD，使A与C重合，若点D在AB的延长线上，则( )A．AB＞CDB．AB＝CDC．AB＜CDD．无法比较AB与CD的长短3．已知A，B是数轴上的两点，AB＝2，点B表示－1，则点A表示( )A．1 B．－3 C．1或－3 D．3或14．A，B两点间的距离是指( )A．连结A，B两点间的线段长度B．过A，B两点间的直线C．连结A，B两点间的线段D．直线AB的长5．为了估计池塘两岸A，B间的距离，小明在池塘一侧选取了一点P，测得PA＝16m，PB＝12m，那么A，B间的距离不可能是( )A．5m B．15m C．20m D．30m6．如图所示，比较图中AB，AC，BC的长度，可以得出AB____________AC，AC____________BC，AB＋BC____________AC.第6题图7．某工程队在修建高速公路时，将如图的弯曲的道路改直，这样做的理由是____________．第7题图8．用”＞”、”＜”或”＝”填空：(1)如果点C在线段AB上，那么AC____________AB，AB____________BC；(2)如果点D在线段AB的延长线上，那么AD____________AB，BD____________AD；(3)如果点C在线段AB的反向延长线上，则BC____________AC.9．如图，利用圆规比较四边形ABCD中四条边的长短，并用”>”连接．第9题图10．如图，线l表示一条小河，点A，点B表示两个村庄，在何处架桥才能使A村到B 村的路程最短？第10题图11．如图所示，沿大街AB段上有四处居民小区A，B，C，D，且有AC＝CD＝DB.为了改善每个小区的居民的购物环境，想在AB上建一家超市，每个小区的居民各执一词，难以定下具体建设位置，如果由你出任超市负责人．从便民、获利的角度考虑，你将把超市建在哪里？第11题图B组自主提高12．为解决村庄用电问题，政府投资在已建电厂与A，B，C，D这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离(单位：km)如图所示，则把电力输送到这四个村庄的输电线路的总长度最短应是( )第12题图A．19.5km B．20.5km C．21.5km D．24.5km13．如图所示，有一正方体纸盒，在点C′处有一只小虫，它要爬到点A吃食物，应该沿着怎样的路线才能使行程最短？你能设计出这条路线吗？第13题图C组综合运用14．如图，一条街道旁有A，B，C，D，E五幢居民楼，其中BC＝DE＝2AB＝2CD.某大桶水经销商统计各居民每周所需大桶水的数量如下表：第14题图他们计划在这五幢楼中租赁一间门市房，设立供水点．若仅考虑这五幢楼内的居民取水所走路程之和最小，你将把门市房选择在哪幢楼中？参考答案6．3线段的长短比较【课堂笔记】1．长度相等 2.线段两点之间线段最短 3.连结两点的线段的长度【分层训练】1．C 2.C 3.C 4.A 5.D6．＜＞＝7.两点之间线段最短8．(1)＜＞(2)＞＜(3)＞9．BC>CD>AD>AB10．连结AB，线段AB与线l的交点P就是架桥之处．第10题图11．超市应建在CD段上12．C13．答案不唯一，如图虚线为一种．第13题图14．设AB＝a，则BC＝2a，CD＝a，DE＝2a.若供水点在A楼，则55a＋50(a＋2a)＋72(a＋2a＋a)＋85(a＋2a＋a＋2a)＝1003a；若供水点在B楼，则38a＋50×2a＋72(2a＋a)＋85(2a＋a＋2a)＝779a；若供水点在C楼，则38(a＋2a)＋55×2a＋72a＋85(a＋2a)＝551a；若供水点在D楼，则38(a＋2a＋a)＋55(2a＋a)＋50a＋85×2a＝537a；若供水点在E楼，则38(a＋2a＋a＋2a)＋55(2a＋a＋2a)＋50(a＋2a)＋72×2a＝797a. ∴桶装水供应点设在D楼时总路程最小．。

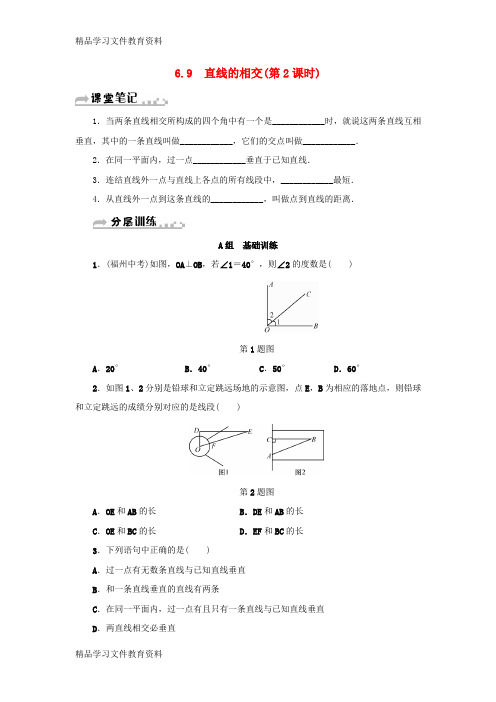
6.9 直线的相交(第2课时)1．当两条直线相交所构成的四个角中有一个是____________时，就说这两条直线互相垂直，其中的一条直线叫做____________，它们的交点叫做____________．2．在同一平面内，过一点____________垂直于已知直线．3．连结直线外一点与直线上各点的所有线段中，____________最短．4．从直线外一点到这条直线的____________，叫做点到直线的距离．A组基础训练1．(福州中考)如图，OA⊥OB，若∠1＝40°，则∠2的度数是( )第1题图A．20° B．40°C．50° D．60°2．如图1、2分别是铅球和立定跳远场地的示意图，点E，B为相应的落地点，则铅球和立定跳远的成绩分别对应的是线段( )第2题图A．OE和AB的长 B．DE和AB的长C．OE和BC的长 D．EF和BC的长3．下列语句中正确的是( )A．过一点有无数条直线与已知直线垂直B．和一条直线垂直的直线有两条C．在同一平面内，过一点有且只有一条直线与已知直线垂直D．两直线相交必垂直4．如图，下列线段中，长度表示点A到直线CD的距离的是( )第4题图A．AB B．CD C．BD D．AD5．已知P为直线m外一点，A，B，C为直线m上的三点，PA＝4cm，PB＝5cm，PC＝2cm，则点P到直线m的距离( )A．等于4cm B．等于2cm C．小于2cm D．不大于2cm6．如图，OB⊥CD，∠1∶∠2＝2∶5，则∠AOB等于( )第6题图A．36°B．126°C．108°D．162°7．根据图形填空：第7题图(1)直线AD与直线CD相交于点____________；(2)____________⊥AD，垂足为点____________；AC⊥____________，垂足为点____________；(3)点B到直线AD的距离是线段____________的____________，点D到直线AB的距离是线段____________的____________；(4)若AB＝2cm，BC＝1.5cm，则点A到直线CD的距离为____________cm.8．(1)如图1，AO⊥OC，∠1＝∠2，则OB与OD的位置关系是____________．图1图2第8题图(2)将一张长方形纸片按如图2所示的方式折叠，BC，BD为折痕，则BC与BD的位置关系为____________．9．(1)一个角的两边与另一个角的两边分别垂直，这两个角的关系是____________．第9题图(2)如图，OA⊥OB，OD⊥OC，若∠AOD＝59°，则∠BOC＝____________；若∠AOC＝20°，则∠BOD＝____________；若∠AOC＝α，则∠BOD＝____________.10．分别过点P画直线AB的垂线．第10题图11．如图，直线AB ，CD 相交于点O ，OE ⊥CD ，OF ⊥AB ，已知∠EOF ＝140°，求∠AOC 的度数．第11题图12．如图，已知两直线AB ，CD 相交于点O ，OE ⊥CD ，且∠EOB ＝13∠BOC.试求∠AOC 的度数．第12题图B 组 自主提高13．(1)已知∠AOB ＝30°，OC ⊥OA ，OD ⊥OB ，则∠COD 的度数为____________． (2)如果点A ，B 都在直线l 的同一条垂线上，点A 到直线l 的距离等于8cm ，点B 到直线l 的距离等于6cm ，那么线段AB 的长为____________cm.14．如图，已知直线AB ，CD ，EF 相交于点O ，CD ⊥AB ，∠AOE ∶∠AOD ＝2∶5，求∠BOF ，∠DOF的度数．第14题图C组综合运用15．如图，直线EF，CD相交于点O，OA⊥OB，且CO平分∠AOF，若∠AOE＝n°，求∠BOD 的度数．(用含n的代数式表示)第15题图参考答案6．9 直线的相交(第2课时)【课堂笔记】1．直角 另一条直线的垂线 垂足 2.有一条而且仅有一条直线 3.垂线段 4.垂线段的长度【分层训练】1．C 2.D 3.C 4.D 5.D 6.B7．(1)D (2)BE E CD C (3)BE 长度 DC 长度 (4)3.5 8．(1)垂直 (2)BC⊥BD9．(1)相等或互补 (2)59° 160° 180°－α 10．画图略 11．∠AOC＝40° 12．∠AOC＝45°13．(1)30°或150° (2)2或14 【解析】分点A ，B 在直线l 的同侧或异侧两种情况讨论：同侧：AB ＝8－6＝2(cm )，异侧：AB ＝8＋6＝14(cm )．14．∠BOF＝36°，∠DOF ＝54°.15．解法一：∵∠AOF＋∠AOE＝180°，∴∠AOF ＝180°－∠AOE＝180°－n °.∵OC 平分∠AOF，∴∠AOC ＝12∠AOF ＝90°－12n °.又∵OA⊥OB，∴∠AOB ＝90°，∴∠BOD ＝180°－∠AOB－∠AOC＝180°－90°－(90°－12n °)＝12n °.解法二：作OH 平分∠AOE，则OH⊥OC.∵OA⊥OB，∴∠DOH ＝∠BOA＝90°，∴∠BOD ＝∠AOH＝12∠AOE ＝12n °.。

6．4 线段的和差知识点1 线段的中点1．如图6－4－1所示，已知C 是线段AB 的中点，D 是线段CB 的中点，那么AC ＝____AB ＝____DB ，DB ＝____CB ＝____AD .图6－4－12．如图6－4－2，P 是线段AB 上的点，其中不能说明P 是线段AB 中点的是( )图6－4－2A ．AB ＝2AP B. AP ＝BPC ．AB ＋BP ＝ABD ．BP ＝12AB知识点2 线段的和差 3．如图6－4－3，看图填空： (1)AC ＝AD －________； (2)BC ＋CD ＝________－AB .图6－4－34．如图6－4－4，AB ＝CD ，则AC 与BD 的大小关系是( )图6－4－4A ．AC ＞BDB ．AC ＜BD C ．AC ＝BD D ．无法确定5．如图6－4－5，C ，D 是线段AB 上的两点，D 是线段AC 的中点，若AB ＝10 cm ，BC ＝4 cm ，则AD 的长为( )图6－4－5A ．2 cmB ．3 cmC ．4 cmD ．6 cm 知识点3 线段作图6．如图6－4－6所示，已知线段a ，b ，利用尺规，求作一条线段AB ，使AB ＝a ＋2b .(不写作法)图6－4－67．已知线段AB ＝6 cm ，在直线AB 上截取线段AC ＝2 cm ，则线段BC 的长是( ) A ．4 cm B ．3 cm 或8 cm C ．8 cm D ．4 cm 或8 cm8．2017·鄞州期末如图6－4－7，线段AB 被点C ，D 分成2∶4∶7三部分，M ，N 分别是AC ，DB 的中点．若MN ＝17 cm ，则BD ＝________cm.图6－4－79．2016·余杭区期末已知线段CD ，按要求画出图形并计算：延长线段CD 到点B ，使DB ＝12CB ，延长DC 到点A ，使AC ＝2DB .若AB ＝8 cm ，求CD 与AD 的长．10．如图6－4－8，已知C是线段AB上的一点，M，N分别是AC，BC的中点．(1)若AB＝18 cm，AC＝10 cm，求MN的长度；(2)若AB＝18 cm，AC＝x cm(0<x<18)，求MN的长度；(3)根据(1)(2)，你能从中发现什么？(4)若AB＝a cm，求MN的长度(用含a的代数式表示)．图6－4－81.12 2 12 132.C3.(1)CD (2)AD 4．C [解析] ∵AB ＝CD ，∴AB ＋BC ＝CD ＋BC ，∴AC ＝BD .5．B [解析] 因为D 是线段AC 的中点，所以AC ＝2AD .因为AC ＝AB －BC ＝6 cm ，所以AD ＝3 cm.故选B.6．解：如图所示，AC ＝a ，CD ＝DB ＝b ，AB ＝a ＋2b .AB 即为所求作的线段．7．]D [解析] 如图所示，可知：①当点C 在线段AB 上时，BC ＝AB －AC ＝4 cm ； ②当点C 在线段BA 的延长线上时，BC ＝AB ＋AC ＝8 cm. 8．14 9．解：如图：∵DB ＝12CB ，∴CD ＝DB .∵AC ＝2DB ，∴AC ＝BC ＝12AB .∵AB ＝8 cm ，∴CD ＝14AB ＝2 cm ，AD ＝34AB ＝6 cm.故CD 的长是2 cm ，AD 的长是6 cm.10．解：(1)MN ＝12×10＋12×(18－10)＝9(cm)．(2)MN ＝12x ＋12(18－x )＝9(cm)．(3)发现：线段MN 的长度始终等于线段AB 长度的一半．1 2AB＝12a cm.(4)MN＝。

6．2 线段、射线和直线1．线段可以用表示它的两个端点的____________表示，也可以用一个____________来表示．2．直线可以用它上面任意两个点的____________表示，也可以用一个____________表示．3．射线用____________和____________的两个字母表示，表示端点的字母要写在____________．4．经过两点____________一条直线，可以简单地说成：____________一条直线．A组基础训练1．数轴是一条( )A．线段 B．射线C．直线 D．以上均可2．下列各图中直线的表示方法正确的是( )3．根据”反向延长线段MN”这句话，下列选项中，正确的是( )4．下列叙述中，正确的是( )A．画直线AB，使AB＝2cmB．画直线AB的中点CC．在射线AB上截取AC，使AC＝1cmD．延长射线AB到点C5．下列说法不正确的是( )A．射线是直线的一部分B．线段是直线的一部分C．直线的长度大于射线的长度D．直线是可以无限延伸的，射线也是可以无限延伸的6．平面上不重合的两点确定1条直线，不同的三点最多可确定3条直线，若平面上不同的n个点最多可确定10条直线，则n的值为( )A．4 B．5 C．6 D．77．笔直的窗帘轨，至少需要____________个钉子才能将它固定，理由是____________．8．如图，图中共有____________条直线，共有____________条射线，共有____________条线段．第8题图9．如图，已知A，B，C，D四个点，请按要求画图：第9题图(1)画线段AC；(2)画射线BD；(3)画直线CD.10．按要求画出图形，并回答问题：(1)画直线l，在直线l上取A，B，C三点，使点C在线段AB上，在直线l外取一点P，画直线BP，射线PC，连结AP；(2)在(1)中所画图中，共有几条直线，几条射线，几条线段？请把所有直线和线段用图中的字母表示出来．11．如图，已知数轴的原点为O，点A所表示的数为3，点B所表示的数为－2.(1)数轴的原点左边的部分(包括原点)是什么图形？怎样表示？(2)射线OA上的点所表示的数是什么数？端点O表示什么数？(3)数轴上表示不小于－2，且不大于3的部分是什么几何图形？怎样表示？第11题图B组自主提高12．A，B两城之间有铁路相通，两城之间有C，D，E，F四个停靠站，则运行于A，B 两城之间的列车，共需制作的火车票有( )A．5种 B．10种C．15种 D．30种13．如图，平面内有六条有公共端点的射线OA，OB，OC，OD，OE，OF，从射线OA开始，按逆时针方向依次在各条射线上写上数字1，2，3，4，5，6，7，….第13题图(1)数20在射线________上；(2)请写出六条射线上数字的排列规律；(3)数xx在哪条射线上？14．平面内有若干条直线，探究最多可将平面分成几个部分：若有1条直线，平面被分成2个部分(1＋1＝2)；若有2条直线，平面最多被分成4个部分(1＋1＋2＝4)；若有3条直线，平面最多被分成7个部分(1＋1＋2＋3＝7)；…(1)若有6条直线，平面最多被分成几个部分？(2)若有n条直线(n为正整数)，平面最多被分成几个部分？C组综合运用15．握手是社交常见的礼节，与人初次见面，往往以握手示礼．新学期开学，老师为了让新同学相互认识，要求全班同学互相握手为礼，并同时彼此介绍自己．试解答下列问题：(1)如果全班有40人，那么一共握手多少次？(2)如果全班有n人，那么一共握手多少次？(3)你能不能从(1)(2)两题中得到启示，如果平面上有n个点，且其中任意三点都不在同一直线上，经过其中任意两点画直线，一共可以画多少条直线？参考答案6．2线段、射线和直线【课堂笔记】1．大写字母小写字母 2.大写字母小写字母 3.表示它的端点射线上另外任意一点前面 4.有一条而且只有两点确定【分层训练】1．C 2.C 3.A 4.C 5.C 6.B7.两两点确定一条直线8.1 8 69．图略10．(1)如图所示；第10题图(2)2条直线，12条射线，6条线段，直线l，直线BP，线段AC，BC，AB，AP，CP，BP.11．(1)射线 射线OB (2)非负数 0 (3)线段 线段AB 12．D13．(1)∵20÷6＝3……2，∴数20在射线OB 上．(2)规律如下：设n 为正整数，则数6n －5在射线OA 上；数6n －4在射线OB 上；数6n －3在射线OC 上；数6n －2在射线OD 上；数6n －1在射线OE 上；数6n 在射线OF 上．(3)∵xx÷6＝336……1，∴数xx 在射线OA 上．14．(1)22 (2)n （n ＋1）2＋1 15．(1)780次 (2)n （n －1）2次 (3)n （n －1）2条。

6.4 线段的和差1．如果一条线段的____________是另两条线段的____________的____________，那么这条线段就叫做另两条线段的和．2．如果一条线段的____________是另两条线段的____________的____________，那么这条线段叫做另两条线段的差．3．两条线段的和或差仍是一条____________．4．若点C把线段AB分成____________的两条线段AC与BC，则点C叫做线段AB的中点．A组基础训练1．如图，AD＝CB，则AC与BD的长度关系是()A．AC>BD B．AC<BD C．AC＝BD D．不能确定第1题图2．如图，如果点C是线段AB的中点，那么①AB＝2AC；②2BC＝AB；③AC＝BC；④AC＋BC＝AB，上述四个式子中，正确的有()第2题图A．1个B．2个C．3个D．4个3．如图，下列关系式中与图形不符合的是()第3题图A．AD－CD＝AB＋BCB．AC－BC＝AD－BDC．AC－BC＝AC＋BDD．AD－AC＝BD－BC4．如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线中() 第4题图A．a户最长B．b户最长C．c户最长页 1 第D．一样长5．如图，C是线段AB上一点，M是线段AC的中点，若AB＝8cm，BC＝2cm，则MC的长是()第5题图A．2cmB．3cmC．4cmD．6cm16．已知线段AB＝6，C在线段AB上，且AC＝AB，点D是AB的中点，那么DC3等于() A．1 B．2 C．3 D．47．如图，直线上有四个点A，B，C，D，看图填空：第7题图(1)AC＝____________＋BC；(2)CD＝AD－____________；(3)AC＋BD－BC＝____________.8．如图所示，M，N在线段AB上，且MB＝4cm，NB＝16cm，且点N是AM的中点，则AB ＝____________cm.第8题图9．如图所示，M，N把线段AB三等分，C为NB的中点，且CN＝5cm，AB＝____________cm. 第9题图10．在一次实践操作中，小张把两根长为23cm的竹竿绑接成一根长40cm的竹竿，则重叠部分的长为____________cm.11．如图，已知线段a，b(a＞b)，画一条线段，使它等于2a－b.第11题图12．先画图，再计算．(1)画线段AB＝2cm，延长线段AB至点C，使AC＝2AB，取线段BC的中点D；页 2 第(2)求线段BD的长．13．如图，A，B是线段MN上的两点，且MA∶AB∶BN＝2∶3∶4，MN＝36cm，求线段AB 和BN的长度．第13题图B组自主提高14．下列说法：①若PA＝PB，则P是线段AB的中点；②到线段两个端点距离相等的点必是线段的中点；③点A，B，C在同一直线上，且AC＝2，BC＝4，点P是AB的中点，则CP＝1.其中不正确的是____________(填序号)．15．已知线段AB＝12cm，点C是直线AB上一点，且AC∶BC＝1∶2，若D是AC的中点，求线段CD的长．C组综合运用16．(1)如图，点C在线段AB上，AC＝10cm，CB＝8cm，M，N分别是AC，BC的中点，求线段MN的长；第16题图(2)若C为线段AB上任一点，AC＋CB＝x(cm)，(1)中其他条件不变，你能猜想MN的长度吗？并说明理由．你能用一句简洁的话描述你发现的结论吗？(3)若点C在线段AB的延长线上，AC－BC＝y(cm)，M，N分别为AC，BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由；(4)把(1)条件中的”如图”去掉，”点C在线段AB上”改成”点C在直线AB上”，其余条件不变，你能得出线段MN的长度吗？参考答案6．4 线段的和差【课堂笔记】1．长度长度和2.长度长度差3.线段4.相等【分层训练】1．C2.D3.C4．D【解析】同一条电线中竖着的线段两两相加，可知每户的两条竖线加起来一样长；每户横着的线段也一样长．5．B 6.A 7．(1)AB(2)AC(3)AD 8．289.3010.6页 3 第11．(1)作射线AP.(2)用圆规在射线AP上截取AB＝BC＝a.(3)用圆规在线段BC的反方向上截取CD＝b.线段AD就是所要作的线段，即AD＝2a－b(见图)．第11题图12．(1)如图：第12题图(2)BD＝1cm.13．设MA＝2x，则AB＝3x，BN＝4x，∴MN＝MA＋AB＋BN＝9x＝36，∴x＝4，∴AB＝3x ＝12cm，BN＝4x＝16cm.14．①②③15．根据题意，有两种情况：①当点C在线段AB上时，如图1.设AC＝x，则BC＝2x.∵AB＝12cm，∴AB＝AC＋BC＝x＋2x＝3x＝12，∴x＝4，∴AC＝4cm.1又∵D是AC的中点，∴CD＝AC＝2cm.2②当点C在线段BA的延长线上时，如图2.第15题图∵AC＝BC＝1∶2，∴A为BC的中点，∴AC＝AB＝12cm.1又∵D为AC的中点，∴CD＝AC＝6cm.2综上所述，CD的长为2cm或6cm.1116．(1)MN＝MC＋CN＝AC＋CB＝5＋4＝9(cm)．22111111(2)MN＝x(cm)．理由：MN＝MC＋CN＝AC＋CB＝(AC＋CB)＝AB＝x(cm)．222222结论：若C为线段AB上任一点，M，N分别是AC，BC的中点，则线段MN的长是线段AB长的一半．页 4 第11111(3)MN＝y(cm)．理由：如图，MN＝MC－NC＝AC－BC＝(AC－BC)＝y(cm)．22222第16题图(4)1cm或9cm.页 5 第。

6.4 线段的和差
一、教学目标：
知识目标：1、让学生了解线段的和，差概念，会画线段的和差
2、引导学生理解线段中点的概念，并会用刻度尺画线段的中点
3、进行有关线段的和，差，倍，分的简单计算的讲解
能力目标：通过实际操作，让学生体会线段的和差在实际生活中的应用，培养学生的抽象思维能力。

情感目标：培养学生的观察力，能把实际问题转化为教学问题，培养学生对数学的好奇心与求知欲。

二、教学重难点：
重点：了解线段的和、差概念，并理解线段中点的概念
难点：会进行有关线段的和、差、倍、分的简单计算
三、教学过程：
（一）导入新课：
如图，从宾馆A出发去景点B有A→C →B, A →D →B两条道路。

你有哪些方法判别哪条路更近些？如果工具只有没有刻度的直尺和圆规呢？
（二）探究新知：
已知线段a=1.5cm，b=2.5cm，c=4cm，a，b，c三条线段之间的长度有什么关系？（引出线段的和差的定义）
例题讲解：
例1. 已知线段a，b.用直尺和圆规作图：
（1）a+b （2）b-a
例2.Ｐ是线段AB的中点，点Ｃ，Ｄ把线段AB三等分．已知线段CP的长为1.5 cm，求线段AB的长．
（三）课内小结：
1、通过本节课的学习你有什么收获？
2、本节课主要学习了那些内容？（1）线段的和差
（2）线段的中点.
（四）课堂练习：
（五）作业布置：。

七年级数学上册第6章图形的初步知识6.2 线段、射线和直线同步练习（新版）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级数学上册第6章图形的初步知识6.2 线段、射线和直线同步练习（新版）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册第6章图形的初步知识6.2 线段、射线和直线同步练习（新版）浙教版的全部内容。

6．2 线段、射线和直线知识点1 线段、射线和直线的认识1．如图6－2－1所示，判断下列说法的正误（在括号内打“√"或“×”)：图6－2－1（1）直线AB与直线BA是同一条直线;（）(2）射线AB与射线BA是同一条射线；（)(3)线段AB与线段BA是同一条线段；( ）(4)射线AB与射线BC是同一条射线;（)（5）射线AB与射线AC是同一条射线；（）（6)射线BA与射线BC是同一条射线．（）2．如图6－2－2中的线段、直线或射线，能相交的是（）图6－2－23．如图6－2－3所示，林林的爸爸只用两个钉子就把一根木条固定在墙上，其依据是____________．图6－2－3知识点2 画图4．按下列语句，不能正确画出图形的是（）A．延长直线ABB．直线EF经过点CC．线段m与n交于点PD．经过点O的三条直线a，b，c5．按照下列要求画图．(1）如图6－2－4①，已知点A，B，C，画直线AB,射线AC，线段BC；（2)如图6－2－4②，已知直线l和直线l外一点A，过点A画一条直线与直线l交于点B。

②图6－2－46．如图6－2－5，A，B，C是直线l上的三个点，图中线段的条数是( )图6－2－5A．1 B．2 C．3 D．47．在平面内,三条直线相交，则交点的个数最多有________个，最少有________个．8．如图6－2－6，点A,B，C,D在同一直线上，回答下列问题：（1)表示出图中所有的线段；（2)图中有几条直线？怎样表示？(3)仅用图中的字母表示出图中所有可以表示的射线．图6－2－69．2017·上杭期末小明和小亮在讨论“枪管上为什么要有准星"．小明：过两点有且只有一条直线，所以枪管上要有准星．小亮：射击时，若将人眼看成一点，准星看成一点，目标看成一点,这不就有三个点了吗？多了一个点呀！请你说说你的观点．10. 往返于A,B两个城市的客车，途中有C,D，E三个停靠点．（1）该客车有________种不同的票价；（2）该客车上要准备________种车票．1．(1）√（2）×(3）√(4)×(5)√（6）×2．A 3。

七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版的全部内容。

6.3 线段的长短比较1．一般地，如果两条线段____________，那么我们就说这两条线段相等．2．在所有连结两点的线中，____________最短，简单地说，____________。

3．____________叫做这两点间的距离．A组基础训练1．下列说法正确的是( )A．直线可以比较长短B．直线比射线长C．线段可以比较长短D．线段可能比直线长2．已知线段AB和线段CD,使A与C重合,若点D在AB的延长线上，则（）A．AB＞CDB．AB＝CDC．AB＜CDD．无法比较AB与CD的长短3．已知A,B是数轴上的两点，AB＝2，点B表示－1，则点A表示（）A．1 B．－3 C．1或－3 D．3或14．A，B两点间的距离是指（)A．连结A，B两点间的线段长度B．过A，B两点间的直线C．连结A，B两点间的线段D．直线AB的长5．为了估计池塘两岸A，B间的距离，小明在池塘一侧选取了一点P,测得PA＝16m,PB＝12m,那么A，B间的距离不可能是（)A．5m B．15m C．20m D．30m6．如图所示，比较图中AB，AC，BC的长度，可以得出AB____________AC，AC____________BC，AB＋BC____________AC。