(完整版)圆柱的认识和表面积练习题.docx

圆柱表面积、体积操作练习题姓名：提示：请同学们先用卡纸制作下列立体图形的模型（制作时请注意预留接口粘贴处），再解决问题。

本次练习共需制作５个模型，你全做对了吗？一、制作一个长、宽、高分别为８厘米、６厘米、４厘米的长方体。

再分别计算出它的表面积和体积。

１、模型是否已经制作？（）。

画出它的草图，标出有关数据：２、长方体的表面积计算公式是：（）这个长方体的表面积：３、长方体的体积计算公式是：（）这个长方体的体积：４、如果把这个长方体看作是一块长方体木料，要将加工成一个最大的圆柱。

这个圆柱的高应该是（）厘米，底面半径是（）厘米。

（可以模型或草图上画一画）这个圆柱的表面积是多少？这个圆柱的体积是多少？二、制作一个棱长为６厘米的正方体。

再分别计算出它的表面积和体积。

１、模型是否已经制作？（）。

画出它的草图，标出有关数据：２、正方体的表面积计算公式是：（）这个正方体的表面积：３、正方体的体积计算公式是：（）这个正方体的体积：４、如果把这个正方体看作是一块正方体木料，要将加工成一个最大的圆柱。

这个圆柱的高应该是（）厘米，底面半径是（）厘米。

（可以模型或草图上画一画）这个圆柱的表面积是多少？这个圆柱的体积是多少？这个圆柱的体积是原来正方体体积的几分之几？三、制作一个底面直径是４厘米，高也是４厘米的圆柱。

１、模型是否已经制作？（）２、画出侧面展开图的草图，并标上有关数据：３、画出该圆柱沿直径劈成相等的两半，所得到的截面的草图，并标出相关数据：４、求出这个圆柱的表面积（写出每一步的计算公式）。

５、求出圆柱的体积（写出每一步的计算公式）。

６、如果把这圆柱看作是一块圆柱形木料，沿横截面切成两段,表面积多出多少？７、如果把这圆柱看作是一块圆柱形木料，沿直径劈成相等的两半，表面积多出多少？四、用一张长25.12厘米，宽18.84厘米的长方形卡纸围成一个圆柱有几种围法？（）１、请以长方形的长作为圆柱的高，制作出１号圆柱，１号圆柱的底面半径是多少厘米？２、求出１号圆柱的表面积（写出每一步的计算公式）。

圆柱的表面积测试题 (含答案解析) 圆柱的表面积测试题一、填空题。

1.把圆柱的侧面沿高剪开，展开得到一个矩形形，这个图形的长等于这个圆柱的高，宽等于这个圆柱的底面周长。

2.一个圆柱的底面半径是5厘米，高是3厘米，它的侧面积是30π平方厘米。

3.圆柱的侧面积加上底面积，就是圆柱的表面积。

4.一个圆柱形易拉罐的底面直径是6厘米，高是15厘米，它的侧面积是90π平方厘米。

5.一个圆柱体的底面半径是5分米，高是8分米，它的侧面积是40π平方分米，表面积是90π平方分米。

6.圆柱的上下两个面叫作底面，它们是相同的两个圆。

7.一个圆柱的底面半径是3厘米，侧面积是150.72平方厘米，这个圆柱的表面积是226.08平方厘米。

8.一个圆柱的底面直径和高都是6厘米，它的侧面积是36π平方厘米。

9.一个圆柱底面周长是15.7分米，高是3分米，它的表面积是94.2平方分米。

10.把一个棱长为4厘米的正方体削成一个最大的圆柱体，这个圆柱体的表面积是32π平方厘米。

二、选择题。

1.如果一个圆柱的体积不变，底面积扩大4倍，那么高应该缩小为原来的1/8.2.圆柱有无数条高。

3.两个圆柱的高相等，底面半径的比是2：3，则侧面积比是4：9.4.把一个直径为4厘米，高为5厘米的圆柱，沿底面直径切割成两个半圆柱，表面积增加了20π平方厘米。

算式是3.14×2×5.三、判断题。

1.当圆柱的高和底面直径相等时，圆柱的侧面展开是一个矩形。

（错误）2.一个圆柱的高不变，底面半径扩大到原来的3倍，它的侧面积就扩大到原来的9倍。

（正确）3.把一根底面半径是4厘米的圆柱形木材料锯成两小段一样的圆柱形木料，则表面积增加了25.12平方厘米。

（错误）4.一个圆柱的底面半径和高都是4分米，则它的侧面积可用式子3.14×4×2来表示。

（错误，应为3.14×4×2×2）四、求下面各圆柱的侧面积。

圆柱认识练习题问题一：圆柱的定义及特征圆柱是一种常见的几何体，它具有以下特征：底面是一个圆，而且与底面平行的平面截面也都是圆。

圆柱具有无数个平行于底面的截面，这些截面都是相似的，并且与底面圆的直径相等。

问题二：圆柱的计算公式1. 圆柱的体积计算公式：圆柱的体积可以通过底面半径r和高h来计算，公式为V=πr^2h，其中π取近似值3.14。

2. 圆柱的表面积计算公式：圆柱的表面积由底面积和侧面积组成。

底面积为πr^2，侧面积为2πrh。

所以圆柱的表面积公式为A=2πr(r+h)。

问题三：圆柱的相关练习题1. 题目一：已知圆柱的底面半径为2cm，高度为10cm，求它的体积和表面积。

解答：根据圆柱的体积公式V=πr^2h，将已知值代入，可以得到V=3.14*2^2*10=125.6 cm^3。

根据圆柱的表面积公式A=2πr(r+h)，将已知值代入，可以得到A=2*3.14*2(2+10)=150.72 cm^2。

2. 题目二：已知圆柱的体积为1570.8 cm^3，底面半径为5cm，求它的高度。

解答：根据圆柱的体积公式V=πr^2h，将已知值代入，可以得到1570.8=3.14*5^2*h，解方程可得h≈32 cm。

3. 题目三：已知圆柱的表面积为3768 cm^2，底面半径为8cm，求它的高度。

解答：根据圆柱的表面积公式A=2πr(r+h)，将已知值代入，可以得到3768=2*3.14*8(8+h)，解方程可得h≈14 cm。

通过以上练习题的解答，我们可以进一步加深对圆柱及其计算公式的理解，提高解题能力。

问题四：圆柱在生活中的应用圆柱作为一种常见的几何体，广泛应用于生活和工程中。

以下是一些圆柱在不同领域中的应用示例：1. 饮品容器：像水杯、礼品套装等容器通常呈圆柱形，方便携带和使用。

2. 柱形家具：像柱形桌、柱形椅等家具通常采用圆柱形状，美观稳定。

3. 油桶、储罐：工业中常用的油桶和储罐形状多为圆柱形，便于储存、运输和使用。

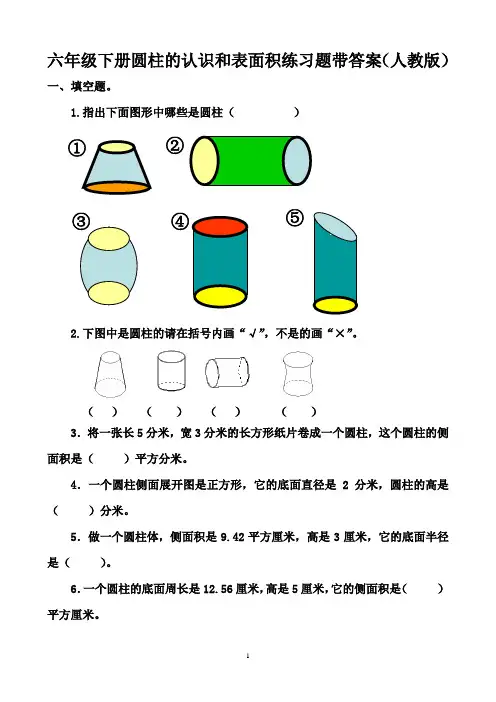
六年级下册圆柱的认识和表面积练习题带答案（人教版）一、填空题。

1.指出下面图形中哪些是圆柱（ ）2.下图中是圆柱的请在括号内画“√”，不是的画“×”。

（ ） （ ） （ ） （ ）3．将一张长5分米，宽3分米的长方形纸片卷成一个圆柱，这个圆柱的侧面积是（ ）平方分米。

4．一个圆柱侧面展开图是正方形，它的底面直径是2分米，圆柱的高是（ ）分米。

5．做一个圆柱体，侧面积是9.42平方厘米，高是3厘米，它的底面半径是（ ）。

6．一个圆柱的底面周长是12.56厘米，高是5厘米，它的侧面积是（ ）平方厘米。

①②③④ ⑤7．创艺广告公司将一张正方形海报贴在一个底面周长为8分米的圆柱形灯箱的侧面，刚好贴满，这个圆柱形灯箱的侧面积是（）平方分米。

8．一个圆柱的底面周长是157分米，高是4分米，侧面积是（）平方米。

9．圆柱的侧面沿高展开是一个（）形或( )行，一个圆柱的底面周长是12.56厘米，高是5厘米，它的侧面积是（）平方厘米。

二、判断：对的打“√”，错的打“×”。

1.圆柱体的高只有一条。

（）2.上下两个底面相等的圆形物体一定是圆柱体。

（）3.圆柱体底面周长和高相等时，沿着它的一条高剪开，侧面是一个正方形。

（）三、选择题。

1．一个圆柱体的侧面积是31.4平方分米，高是2分米，它的底面半径是（）分米。

A．2.5 B．5 C．15.7 D．3.14 2．把一个圆柱的侧面展开，得到一个正方形，这个圆柱的半径是5厘米，它的高是（）厘米。

A．10 B．5 C．31.4 D．78.5 3．把一根圆柱形木材截成两段，它的表面积会（）A．增大 B．减少 C．不变4．如果两个圆柱的侧面积相等，那么它们的底面周长（）A．一定相等B．一定不相等 C．不一定相等5．两个圆柱，甲的底面直径4分米，高5分米，乙的底面直径5分米，高4分米，它们的表面积相比，（）A．甲大 B．乙大 C．相等 D．不能确定6．求制作一个烟囱需要多少铁皮，是求它的（）A.侧面积+2个底面积B.侧面积+1个底面积C.侧面积7．把圆柱的侧面展开，不可能得到（）A．平行四边形 B．正方形 C．梯形8．决定圆柱侧面积的大小的是（）A.圆柱的高B.底面周长C.底面半径和高四、解决问题。

圆柱表面积练习题：一、求下列各图侧面积和表面积二、应用题1、把一个圆柱体的侧面展开，得到一个长31.4厘米，宽10厘米的长方形，这个圆柱体的侧面积是多少平方厘米？表面积是多少平方厘米？2、一个圆柱体的底面直径是5分米，高也是5分米，这个圆柱体的表面积是多少平方分米？3、把一根底面直径是4分米，高是10分米的圆柱形木材，沿着直径对半锯开，每块木材的表面积是多少？表面积增加了多少平方分米？4、有铁皮30平方米，最多能做底面直径和高都是3分米的无盖水桶多少个？（得数保留整数）5、公园的凉亭有6根圆柱形柱子，每根柱子底面半径是4分米，高是5分米，要油漆这些柱子，每平方米用油漆0.3千克，共需要油漆多少千克？下底面不漆，得数保留两位小数）6、一个无盖的圆柱形铁皮水桶，底面直径是30厘米，高是45厘米。

做这样一对水桶，至少需用铁皮多少平方厘米？7、一个圆柱，侧面展开后是一个边长9.42分米的正方形。

这个圆柱的底面直径是多少分米？8、一个圆柱，它的高增加1厘米，它的侧面积就增加50.24平方厘米，这个圆柱的底面半径是多少厘米？9、把一根直径是20厘米，长是2米的圆柱形木材锯成同样的3段，表面积增加了多少平方厘米？10、一个无盖的圆柱形铁皮水桶, 高50厘米, 底面直径30厘米, 做这个水桶大约需用多少铁皮? (得数保留整数)11、一个圆柱形蓄水池，底面周长25.12米，高4米，沿着这个蓄水池的四周及底部抹水泥。

如果平方米用水泥20千克，一共需多少千克水泥？12、一节铁皮烟囱长1.5米，直径是0.2米，做这样的烟囱500节，至少要用铁皮多少平方米？13、有一张长方形铁皮，剪下两个园及一个长方形，正好可以做成一个圆柱，这个圆柱的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？14、一台压路机的滚筒是一个圆柱体，宽1.2米，直径是0.8米，如果它滚动10周，压路的面积是多少？15、下面是一张长方形纸板，按图示剪下阴影部分刚好能做成一个圆柱体，求做好的圆柱体的表面积。

圆柱侧、表面积计算练习题姓名：（本试卷满分100分）一、填空题（本题满分20分，每题2分）：1．圆柱的上、下两个面叫做（），是两个( )的圆形。

2. 圆柱的侧面是一个（），侧面展开是一个（），这个图形的长相当于圆柱（），宽相当于圆柱的（）。

3. 圆柱两个底面之间的距离叫做（）．圆柱有（）条高。

4. 圆柱的侧面积等于（），表面积等于（）．5．圆锥的底面是个（）；侧面是个（），侧面展开后是一个（）。

6．从圆锥的（）的距离是圆锥的高．7．圆柱的底面是两个面积相等的( )，侧面展开相当于一个( ).8．以直角三角形的一条直角边为轴，旋转一周，可以得到一个（）；以长方形的一条边为轴，旋转一周，可以得到一个（）。

9．用一张长15cm，宽8cm的长方形纸围成一个圆柱，这个圆柱的侧面积是( )cm²。

10．一个圆柱的底面积是24cm²，高是12cm，这个圆柱的表面积是( ) cm²。

11．做一节底面直径是20厘米，长60厘米的通风管，至少需要铁皮( )平方厘米．二、选择。

（本题满分10分，每题2分）1、一个圆柱的侧面展开以后正好是一个正方形，那么圆柱的高等于它的底面（）。

A .半径 B.直径 C.周长 D.面积2、在下图中，以直线为轴旋转，可以得出圆柱体的是（），得出圆锥体的是（）。

A B C D3、右图是等底等高的圆锥和圆柱，从不同方向看会看到不同的形状。

从上面看到的形状是（），从左面看到的形状是( ) 。

A B C D4、一个圆柱侧面展开是一个正方形，它的高是半径的（）倍。

A 2B 2∏C 6.285、将一个底面直径为4厘米，高5厘米的圆柱切成两个完全相等的部分，（）切法表面积增加的大。

三、直接写出得数。

（5分）3．14×5= 0.375+58 = 3.14×7= 3.14×9= 1- 16 +56= 0.2÷2%= 3.14×8= 18.84÷6= 4-4÷5= 4÷(14 - 15)= 二、应用题（本题满分65分）：1. （本题满分4分）一个圆柱，底面直径是50厘米，高是18分米，侧面积是多少平方分米？2. （本题满分5分）求如图所示做无盖铁皮水桶要用多少cm ²铁皮？3. （本题满分9分）（1）求圆柱体的表面积:底面圆的周长是12. 56分米,高20厘米;（2）求下列圆柱体的侧面积：①底面半径是4分米,高21厘米; ②底面直径是16厘米,高3厘米;4. （本题满分6分）挖一个圆柱体形的蓄水池,从里面量底面周长31. 4米,深2. 4米。

（完整版）圆柱的表面积练习题
圆柱的表面积（练习）班级姓名
1.一顶帽子，上面是圆柱形，用黑布做；帽檐部分是一个圆环，用红布做。

做这顶帽子，哪种颜色的布用的多？
2.某种饮料罐的形状为圆柱形，底面直径为6cm，高为12cm，将24罐这种饮料按如图所示的方式放入箱内，这个箱子的长、宽、高至少是多少厘米？
3、林叔叔做了一个圆柱形的灯笼（如图）。

上下底面的中间分别留出了78.5cm2的口，他用了多少彩
纸？4.要将路灯柱（如图，圆柱的下底面不刷漆）漆上白色的油漆，要漆多少平方米？街心花园有30个这样的灯柱，如果油漆灯柱每平方米人工费5元，一共需要人工费多少元？
5、一根圆柱形木料的底面半径是0.3m，长是2m。

如图所示，将它截成4段，这些木料的表面积比原木料增加了多少平方米？
1、一顶帽子的帽顶部分是一个用硬纸板做的圆柱，帽檐部分是一个用同样的硬纸板做的圆环，已知帽顶的半径、高、帽檐的宽都是10厘米，做这顶帽子至少要用多少平方分米的硬纸板？
2、工人师傅要在一个零件（如右图）的表面涂一层防锈材
料，这个零件上涂防锈材料的面积是
多少？
3.把一个底面周长是37.68cm，高是10cm的圆柱，沿底面直径切割后，表面积比原来圆柱的表面积增加了多少平米？
4.思考：用一个棱长是6分米的正方体，削成一个最大的圆柱，这个圆柱的表面积是多少？
5、一根圆柱形木料将它截成4段，每一小段的底面半径是0.3m，长是0.5m。

如图所示，如果把这四小段粘在一起，这些木料的表面积比原木料减少了多少平方米？。

圆柱的表面积练习题及答案圆柱的表面积练习题及答案圆柱是一种常见的几何体，它具有圆柱面和两个底面。

计算圆柱的表面积是数学中的基本技能之一。

本文将提供一些圆柱的表面积练习题，并给出答案和解析。

练习题1：一个圆柱的底面半径为5厘米，高度为10厘米。

求该圆柱的表面积。

解析：圆柱的表面积由两个底面和一个侧面构成。

首先，计算底面的面积。

底面是一个圆形，其半径为5厘米，面积可以用公式πr²来计算。

所以，底面的面积为π(5²)=25π平方厘米。

接下来，计算侧面的面积。

侧面是一个矩形，其长度等于底面的周长，宽度等于圆柱的高度。

底面的周长可以用公式2πr来计算，所以侧面的面积为2πr×h=2π×5×10=100π平方厘米。

最后，将底面的面积和侧面的面积相加，即可得到圆柱的表面积。

表面积=底面的面积+侧面的面积=25π+100π=125π平方厘米。

练习题2：一个圆柱的底面直径为8厘米，高度为15厘米。

求该圆柱的表面积。

解析：首先，计算底面的半径。

底面的直径为8厘米，所以半径等于直径的一半，即4厘米。

接下来，计算底面的面积。

底面是一个圆形，其半径为4厘米，面积可以用公式πr²来计算。

所以，底面的面积为π(4²)=16π平方厘米。

然后，计算侧面的面积。

侧面是一个矩形，其长度等于底面的周长，宽度等于圆柱的高度。

底面的周长可以用公式2πr来计算，所以侧面的面积为2πr×h=2π×4×15=120π平方厘米。

最后，将底面的面积和侧面的面积相加，即可得到圆柱的表面积。

表面积=底面的面积+侧面的面积=16π+120π=136π平方厘米。

练习题3：一个圆柱的底面半径为6厘米，高度为20厘米。

求该圆柱的表面积。

解析：首先，计算底面的面积。

底面是一个圆形，其半径为6厘米，面积可以用公式πr²来计算。

所以，底面的面积为π(6²)=36π平方厘米。

圆柱的认识练习题姓名一、填空1、圆柱的上下两个圆面叫做（），它们是（）的两个圆形；周围的面叫做（）；圆柱两个底面之间的距离叫做（）。

一个圆柱有（）条高。

2、圆柱的侧面是一个（）面，把它展开得到一个长方形，长方形的长等于圆柱的（），宽等于圆柱的（）。

当圆柱的底面周长和高相等时，把它的侧面展开得到一个（）形。

3、把一张长方形的纸的一条边固定贴在一根木棒上，然后快速转动，得到一个（）。

4、一个圆柱的侧面展开后得到一个长方形，长是12.56厘米，宽是3厘米。

这个圆柱的底面周长是（）厘米，底面直径是（）厘米，高是（）厘米。

5、一个圆柱的侧面展开后得到一个正方形，边长是9.42厘米。

这个圆柱的底面周长是（）厘米，高是（）厘米，底面半径是（）厘米。

6、一个圆柱的侧面展开正好是一个正方形，它的高是直径的( )倍。

7、把一个底面直径9厘米的圆柱的侧面展开，得到一个正方形，圆柱的高是（）厘米。

8、同一个圆柱底面之间的距离处处相等.( )二、判断1、啤酒瓶是圆柱体。

( )2、圆柱的侧面沿着高展开后会得到一个长方形或者正方形。

( )3、同一个圆柱底面之间的距离处处相等.( )4、一个圆柱，底面周长是12.56厘米，高是12.56厘米。

这个圆柱的侧面沿着高展开，得到一个长方形。

( )5、一个圆柱，底面周长是12.56厘米，高是12.56厘米。

这个圆柱的侧面沿着高展开，得到一个正方形( )。

6、一个圆柱，底面半径是4厘米，高是4厘米。

这个圆柱的侧面沿着高展开，得到一个正方形。

( )7、圆柱体的高只有一条。

（）8、上下两个底面相等的圆形物体一定是圆柱体。

（）9、圆柱体底面周长和高相等时，沿着它的一条高剪开，侧面是一个正方形。

（）10、圆柱两底面之间的连线叫做圆柱的高。

（）11、上下两个底面相等的物体一定是圆柱体。

（）三、选择1、一个圆柱的侧面展开正好是一个正方形，这个圆柱的底面直径与高的比是（）A．1：π B. π：1 C. 1：2π D. 2π：1 2、圆柱有（）个面。

圆柱、圆锥的认识，圆柱的表面积练习一例题：一个圆柱体木块，底面半径是6cm，高是10cm，截成两个圆柱体之后，表面积增加多少cm²？练习1、一个圆柱体木头，底面半径是8cm，高是230cm，现截成两个圆柱体木头，表面积增加多少？2.把一个直径20cm的圆柱形木头锯成3段，表面积要增加多少？练习二例题：一个圆柱，高减少2cm，表面积就减少18.84cm²，求这个圆柱的底面积是多少？练习1、一个圆柱体，高减少4cm，表面积就减少75.36cm²，求这个圆柱体的底面积。

2、一个圆柱体，高增加5cm，表面积就增加125.6cm²，求这个圆柱体的底面积。

3、一根长2m的圆柱形木头，截去2分米的一段小圆柱后，表面积减少了12.56平方分米，那么这根木头原来的体积是多少？练习三例题：如下图，高都是10厘米，底面半径分别是3厘米、6厘米的两个圆柱组成了一个几何体。

求这个物体的表面积。

练习1、高都是2分米，底面半径分别是2分米和5分米的两个圆柱组成的几何体。

求这个物体的表面积。

2、某零件如图，两圆柱的高分别是4cm、2cm，地面半径分别是1厘米和3厘米。

求这个零件的表面积。

例4、圆柱的高都是1米，底面半径分别是0.5米、1米和1.5米。

求这个物体的表面积和体积。

练习四例题：在一个边长4厘米的正方形的六个面各中心挖去一个地面半径为1厘米，深1.5厘米的圆柱，求它的表面积。

练习1、在一个边长为4厘米的正方体各面中心都挖去一个棱长1厘米的小正方体，求挖去后这个物体的表面积。

1、把一张长9.42分米，宽3.14分米的长方形铁皮圈成一个圆柱形无盖容器，要配上底面半径多少分米的圆形铁皮。

2、一个圆柱体底面周长和高相等，如果高缩短了2厘米，表面积就减少12.56平方厘米。

求这个圆柱体的表面积。

3、取出直角三角尺（30度、60度、90度），进行操作观察：将三角尺的一条直角边平放在桌面上，以另一条直角边为轴作快速的旋转，看到了什么？试画出示意图。

圆柱表面积练习题圆柱是一个经典的几何形体，它常常出现在数学和工程问题中。

在这篇文章中，我们将重点讨论圆柱的表面积，并提供一些练习题供读者练习。

一、圆柱表面积的计算公式对于一个圆柱来说，它的表面包括两个底面和一个侧面。

根据几何原理，圆柱的表面积可以通过以下公式进行计算：表面积 = 底面积 + 侧面积其中，底面积等于圆的面积，侧面积等于圆的周长乘以圆柱的高度。

二、练习题1. 小明制作了一个圆柱形的桶，底面半径为5米，高度为10米。

请计算桶的表面积。

解答：首先计算底面积，使用圆的面积公式：底面积= π * 半径^2= 3.14 * 5^2= 3.14 * 25= 78.5 平方米接下来计算侧面积，使用圆的周长公式：= 2 * π * 半径 * 高度= 2 * 3.14 * 5 * 10= 314 平方米最后将底面积和侧面积相加：表面积 = 底面积 + 侧面积= 78.5 + 314= 392.5 平方米所以，这个圆柱桶的表面积为392.5平方米。

2. 现在小明又制作了一个圆柱形的水管，底面半径为2米，高度为15米。

请计算水管的表面积。

解答：同样先计算底面积：底面积= π * 半径^2= 3.14 * 2^2= 3.14 * 4= 12.56 平方米然后计算侧面积：= 2 * π * 半径 * 高度= 2 * 3.14 * 2 * 15= 188.4 平方米最后将底面积和侧面积相加：表面积 = 底面积 + 侧面积= 12.56 + 188.4= 200.96 平方米因此，这个水管的表面积为200.96平方米。

通过以上两个练习题，我们学会了计算圆柱表面积的方法。

希望读者通过这些练习能够巩固所学知识。

如果还有其他关于圆柱表面积的问题，欢迎留言讨论。

谢谢！。

（完整版）六年级圆柱表面积的练习题及答案六年级圆柱表面积的练习题及答案1、.6米 = 厘米分米 = 米7.5平方分米 = 平方厘米9300平方厘米 = 平方米2、填空：圆柱的面积加上的面积，就是圆柱的表面积。

把一个底面积是15.7平方厘米的圆柱，切成两个同样大小的圆柱，表面积增加了平方厘米。

计算做一个圆柱形的茶叶筒要用多少铁皮，要计算圆柱的。

计算做一个圆柱形的烟囱要用多少铁皮，要计算圆柱的。

计算做一个没有盖的圆柱形水桶要用多少铁皮，要计算圆柱的。

一个圆柱，它的高是8厘米，侧面积是200.96平方厘米，它的底面积是。

3、求下面各圆柱的表面积。

底面半径是2分米，高是7.3分米。

底面周长是18.84米，高是5米。

4、选择正确答案的序号填在括号里。

圆柱的侧面积等于乘以高。

A、底面积B、底面周长C、底面半径把一个直径为4厘米，高为5厘米的圆柱，沿底面直径切割成两个半圆柱，表面积增加了多少平方厘米？算式是A、3.14×4×5×B、4×C、4×5×25、一个圆柱形无盖的水桶，底面的直径是0.6米，高是40厘米，做这样一个水桶，需要多少平方米的铁皮？6、一个圆柱形水池，底面内半径是2米，高是1.5米，在池内周围和底面抹上水泥，抹水泥的面积是多少？圆柱的表面积1、填空。

一个圆柱体，底面周长是125.6厘米，高是12厘米，它的侧面积是平方厘米。

一个圆柱体，底面半径是3厘米，高是5厘米，它的侧面积是平方厘米，表面积是平方厘米。

把一张长8分米，宽5分米的白纸，围成一个圆柱形纸筒，这个纸筒的侧面积是平方分米。

一个圆柱体，底面半径是3厘米，高是15厘米，它的表面积是平方厘米。

2、判断。

圆柱体的表面积=底面积×2＋底面积×高。

圆柱体的表面积一定比它的侧面积大。

圆柱体的底面积越大，它的表面积就越大。

3、选择。

做一个无盖的圆柱体的水桶，需要的铁皮的面积是A．侧面积+一个底面积 B.侧面积+两个底面积C.×2一个圆柱的底面直径是10厘米，高是4分米，它的侧面积是平方厘米。

圆柱的表面积练习题1. 圆柱的定义圆柱是一种立体图形，由两个平行的圆底面和连接两个底面的面构成。

底面和底面之间的面是圆柱的侧面。

圆柱具有以下特点： - 圆柱的底面是圆形的，具有半径r。

- 圆柱的高度是两个底面之间的距离，记作h。

2. 圆柱的表面积公式圆柱的表面积是指圆柱的上下底面以及侧面的总面积。

根据圆柱的定义，我们可以得出圆柱的表面积公式：表面积= 2πr² + 2πrh其中，π是一个常数，约等于3.14159。

3. 练习题问题1：已知圆柱的底面半径r为5cm，高度h为8cm，求圆柱的表面积。

根据圆柱的表面积公式，代入已知数值进行计算：表面积= 2πr² + 2πrh= 2π * (5cm)² + 2π * (5cm) * (8cm)= 2π * 25cm² + 2π * 40cm²= 157.08cm² + 251.33cm²≈ 408.41cm²所以，已知底面半径为5cm，高度为8cm的圆柱的表面积约为408.41cm²。

问题2：已知圆柱的底面半径r为12cm，表面积为678.58cm²，求圆柱的高度h。

将圆柱的表面积公式改写为关于高度h的方程：表面积= 2πr² + 2πrh678.58cm² = 2π * (12cm)² + 2π * (12cm) * h根据上述方程，我们可以解出高度h的值。

但由于解方程可能较为繁琐，我们可以使用数值方法进行求解，例如二分法、牛顿迭代法等。

这里以二分法为例进行求解。

首先，我们在一个合理的范围内设定两个边界值，例如h的最小值为0cm，最大值为20cm。

然后，按照二分法的思路进行迭代，不断缩小边界值的范围，直到找到满足条件的高度h。

具体步骤如下： - 初始化边界值： - 最小边界值low = 0 - 最大边界值high = 20 - 进入循环，直到找到满足条件的高度h： - 计算当前的中间值mid = (low + high) / 2 - 根据中间值mid计算对应的表面积surface_area = 2π *(12cm)² + 2π * (12cm) * mid - 判断表面积与目标表面积的关系： - 若surface_area > 678.58cm²，说明中间值偏大，将high更新为mid - 若surface_area < 678.58cm²，说明中间值偏小，将low更新为mid - 若surface_area ≈ 678.58cm²，说明找到了满足条件的高度h - 循环结束后，得到满足条件的高度h的近似值。

进阶练习题
总结词
应用与拓展
详细描述
进阶练习题在基础之上，增加了对圆柱表面积计算的复杂应用。这些题目可能涉及到多个圆柱体的组合、不同角 度的切割、以及与其他几何形状的结合等。通过这些练习，学生可以进一步提高对圆柱表面积的理解和应用能力。
挑战练习题
总结词
创新与挑战
详细描述
挑战练习题是难度较高的题目，需要学生具备一定的创新思维和解题技巧。这些题目可能涉及到圆柱 表面积与其他数学概念的结合，如代数、函数、解析几何等。通过挑战练习，学生可以激发自己的创 新思维，提升解决复杂问题的能力。
THANKS
感谢观看
05
圆柱表面积的实际应用
在日常生活中的应用
制作容器
圆柱形的包装盒、水桶、花盆等 日常用品都需要计算圆柱表面积 来设计和制作。
食品行业
在食品行业中，圆柱形的蛋糕、 面包等食品的外包装需要用到圆 柱表面积的计算。
在工程设计中的应用
机械制造
在机械制造中，圆柱形零件如轴承、气瓶等的表面积需要精确计算，以确保零件的制造 质量和性能。
详细描述
在进行圆柱表面积计算时，需要同时 考虑底面和顶面的面积，以确保总面 积的准确性。如果忽略了任何一个面 的面积，就会导致最终结果偏小。
计算周长时出错
总结词
学生在计算圆柱的侧面周长时，常常 会犯错误，导致周长值不准确。
详细描述
圆柱的侧面是一个曲面，其周长的计 算涉及到圆的周长和圆柱的高。学生 在计算过程中可能会混淆这两个参数， 或者在计算圆的周长时出错，导致最 终的周长值不准确。
对公式理解不透彻导致计算错误
总结词
学生对于圆柱表面积的计算公式理解不 够深入，导致在应用公式时出现错误。

圆柱的表面积经典练习题圆柱的表面积练题一、填空1.把一个底面积是15.7平方厘米的圆柱，切成两个同样大小的圆柱，表面积增加了（31.4）平方厘米。

2、一个圆柱体零件，高10cm，如果沿着它的一条底面直径往下切，切成大小相同的两份，表面积增加80cm²，那么原来这个圆柱体的表面积是（360）cm²。

3、一个圆柱体，底面周长是94.2厘米，高是25厘米，它的侧面积是（942）平方厘米。

4、一个圆柱体，底面半径是2厘米，高是6厘米，它的侧面积是（24）平方厘米。

5、一个圆柱体的侧面积是12.56平方厘米，底面半径是2分米，它的高是（2）厘米。

6、把一张长8分米，宽5分米的白纸，围成一个圆柱形纸筒，这个纸筒的侧面积是（80）平方分米。

7、把一张边长为5.5厘米的正方形白纸，围成一个圆柱形纸筒，这个纸筒的侧面积是（33）平方分米。

8、一台压路机的前轮是圆柱形，轮宽1.3米，直径1.2米，前轮转动一周，压路的面积是（4.752）平方米。

9、把一根直径是20厘米，长是2米的圆柱形木材锯成同样的3段，表面积增加了（1200）立方厘米。

二、判断1、圆柱的侧面展开后一定是长方形。

（错误）2、6立方厘米比5平方厘米显然要大。

（错误）3、一个物体上、下两个面是相等的圆面，那么，它一定是圆柱形物体。

（正确）4、把两张相同的长方形纸，分别卷成两个形状不同的圆柱筒，并装上两个底面，那么制的圆柱的高、侧面积、表面积一定相等。

（错误）5、圆柱体的表面积＝底面积×2＋底面积×高。

（错误）6、圆柱体的表面积一定比它的侧面积大。

（正确）7、圆柱体的高越长，它的侧面积就越大。

（正确）8、圆柱的高与底面直径相等，它的侧面展开图是正方形。

（正确）9、如果两个圆柱的侧面积相等，那么它们的底面周长也相等。

（错误）10、做一节圆柱形通风管要用多少铁皮，就是求它的侧面积。

（正确）三、选择题1、做一个无盖的圆柱体的水桶，需要的铁皮的面积是（侧面积＋两个底面积）×2.2、已知圆柱的底面半径为r，高为h，求这个圆柱表面积的式子是（2πr²+2πrh）。

圆柱的表面积和体积练习题精选
姓名：
一、知识归纳
求表面积：求体积：
（1）侧面积S侧=2πrh （1）底面积S底=πr2 （2）底面积S底=πr2 （2）体积 V=S底h (3)表面积S表=S侧+2S底
(1)已知圆的半径和高，怎样求圆柱的表面积和体积？
（2）已知圆的直径和高，怎样求圆柱的表面积和体积？
（3）已知圆的周长和高，怎样求圆柱的表面积和体积？
二、求下面各圆柱的表面积和体积
⑴底面积28.26平方米，高2米
⑵半径3厘米，高15厘米
⑶直径8分米，高12分米
⑷底面周长25.12米，高3米
⑸底面半径为3厘米，侧面展开图是正方形
3、一个圆柱形水池，直径16米，深1.5米。

（1）这个水池占地面积是多少？（2）在池底及池壁抹一层水泥，抹水泥部分的面积是多少？
（3）挖成这个水池，共需挖土多少立方米？
三、综合练习
1、一个无盖的圆柱形，侧面积是1884平方厘米，底面周长是28.26厘米。

做这个水桶至少要多少平方分米的铁皮？这个水桶的容积是多少立方分米？
2、压路机的滚筒是个圆柱，它的长是1.8米，滚筒横截面半径是0.8米，如果滚筒每分钟滚动12周，那么1小时可压路多少平方米？前进了多少米？
3、在直径8米的水管中，水流速度是每秒2.5米，那么5分钟流过的水有多少立方米？
4、把一个长、宽、高分别是10厘米、8厘米、5厘米的长方体铁块和一个棱长是5厘米的正方体铁块，熔铸成一个圆柱体。

这个圆柱体的底面直径是30厘米，高是多少厘米？
5、想一想，把圆锥的侧面展开会得到一个什么图形？这个图形的一些线段分别和原来圆锥的那些线段相等？怎样计算圆锥的底面积？。

圆柱的表面积练习题圆柱是一种常见的几何体，其具有特定的表面积计算公式。

本文将为您提供一些圆柱的表面积练习题，帮助您巩固对该公式的理解和应用。

在解答每个练习题之前，我们先来简要回顾一下圆柱的定义和表面积公式。

圆柱是由两个平行且相等圆的底面和连接两个底面的侧面组成的立体。

底面的圆心到底面上的任意一点都是相等的距离，称为圆柱的半径（r）。

连接两个底面圆心的直线称为轴线，垂直于底面的直线段称为高（h）。

根据这些参数，我们可以计算圆柱的表面积。

圆柱的表面积由以下三部分构成：两个底面的面积加上侧面的面积。

底面的面积等于圆的面积，即A1=πr^2。

侧面的面积由一个矩形和两个圆的部分组成，矩形的长等于底面圆周长（2πr），宽等于圆柱的高（h），因此侧面的面积为A2=2πrh。

综上所述，圆柱的表面积公式为A=2πr^2+2πrh，其中A表示圆柱的表面积。

现在，让我们来解答一些圆柱的表面积练习题。

练习题1：一个圆柱的半径为3cm，高为8cm，请计算其表面积。

解答1：根据表面积公式A=2πr^2+2πrh，我们将给定的数值代入公式中，计算得到：A=2π(3)^2+2π(3)(8)=2π(9)+2π(24)=18π+48π=66π所以，该圆柱的表面积为66π平方厘米。

练习题2：一个圆柱的底面圆的直径为10cm，高为15cm，请计算其表面积。

解答2：首先，我们需要求得圆柱的半径。

由于底面圆的直径为10cm，所以半径为直径的一半，即r=10/2=5cm。

将半径和高代入表面积公式，计算得到：A=2π(5)^2+2π(5)(15)=2π(25)+2π(75)=50π+150π=200π因此，该圆柱的表面积为200π平方厘米。

练习题3：一个圆柱的高为6m，表面积为180π平方米，请计算其底面圆的半径。

解答3：设底面圆的半径为r。

由题意可知，表面积为180π平方米，根据表面积公式可得：180π=2πr^2+2πrh将给定的高（h=6m）代入上式，化简得：180π=2πr^2+12πr将公式化为一元二次方程：2r^2+12r-180=0通过求解方程，我们可以得到两个解，但由于半径不能为负值，故我们只取正解：r=(-12+√(12^2-4(2)(-180)))/(2(2))=(-12+√(144+1440))/(4)=(-12+√1584)/4≈(-12+39.8)/4=27.8/4=6.95所以，该圆柱的底面圆的半径约为6.95米。