人教A版数学必修四《第一章三角函数》质量评估

阶段质量评估(二) 三角函数(B)(本栏目内容，在学生用书中以独立形式分册装订)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若函数y ＝sin 2x 的图象向左平移π4个单位得到y ＝f (x )的图象，则( )A ．f (x )＝cos 2xB ．f (x )＝sin 2xC ．f (x )＝－cos 2xD ．f (x )＝－sin 2x解析： 依题意得f (x )＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π4＝sin ⎝⎛⎭⎫2x ＋π2＝cos 2x .故选A. 答案： A2．已知cos ⎝⎛⎭⎫π2＋φ＝32，且|φ|＜π2，则tan φ＝( ) A ．－32B ．33C ．－ 3D ． 3解析： 由cos ⎝⎛⎭⎫π2＋φ＝32，得sin φ＝－32，又|φ|＜π2，∴cos φ＝12，∴tan φ＝－ 3. 答案： C3．函数y ＝1－sin x ，x ∈[0,2π]的大致图象是( )解析： 取x ＝0，则y ＝1，排除C 、D ；取x ＝π2，则y ＝0，排除A ，选B.答案： B4．在平面直角坐标系中，已知角α的终边经过点P (a ，a －3)，且cos α＝55，则a 等于( ) A ．1 B ．92C ．1或92D ．1或－3解析： 由题意得a a 2＋(a －3)2＝55，两边平方化为a 2＋2a －3＝0，解得a ＝－3或1，而a ＝－3时，点P (－3，－6)在第三象限，cos α＜0，与题不符，舍去，选A.答案： A5．已知函数y ＝tan(2x ＋φ)的图象过点⎝⎛⎭⎫π12，0，则φ可以是( ) A ．－π12B ．－π6C.π12D ．π6解析： 根据题意可得2×π12＋φ＝k π，k ∈Z ，所以φ＝－π6＋k π，k ∈Z ，取k ＝0，则φ＝－π6.答案： B6．设α是第二象限角，且⎪⎪⎪⎪cos α2＝－cos α2，则α2是( ) A ．第一象限角 B ．第二象限角 C ．第三象限角D ．第四象限角解析： 由题意知2k π＋π2＜α＜2k π＋π(k ∈Z )，则k π＋π4＜α2＜k π＋π2(k ∈Z )，当k ＝2n (n ∈Z )时，α2是第一象限角；当k ＝2n ＋1(n ∈Z )时，是第三象限角．而⎪⎪⎪⎪cos α2＝－cos α2⇒cos α2≤0，∴α2是第三象限角，故选C. 答案： C7．如果函数f (x )＝sin(πx ＋θ)(0＜θ＜2π)的最小正周期为T ，且当x ＝2时，取得最大值，那么( )A ．T ＝2，θ＝π2B ．T ＝1，θ＝πC ．T ＝2，θ＝πD ．T ＝1，θ＝π2解析： ∵T ＝2ππ＝2，f (x )＝sin(πx ＋θ)，∴f (2)＝sin(2π＋θ)＝sin θ＝1，又0＜θ＜2π，则θ＝π2.故选A.答案： A8．下列函数中，最小正周期为π且在⎣⎡⎦⎤0，π2上是减函数的是( ) A ．y ＝sin ⎝⎛⎭⎫x ＋π4 B ．y ＝cos ⎝⎛⎭⎫x ＋π4 C ．y ＝sin 2xD ．y ＝cos 2x解析： y ＝cos 2x 的周期T ＝2π2＝π，因为y ＝cos 2x 的单调递减区间为⎣⎡⎦⎤k π，π2＋k π，k ∈Z ，所以其在⎣⎡⎦⎤0，π2上为减函数，故选D. 答案： D9．将函数y ＝sin(2x ＋φ)的图象向左平移π8个单位后得到一个偶函数的图象，则φ的一个可能取值为( )A.3π4 B ．π4C ．0D ．－π4解析： 将函数y ＝sin(2x ＋φ)的图象向左平移π8个单位，可以得到y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8＋φ＝sin ⎝⎛⎭⎫2x ＋π4＋φ的图象． 此函数为偶函数知φ＋π4＝k π＋π2(k ∈Z )，即φ＝k π＋π4(k ∈Z )．当k ＝0时，φ＝π4，故选B.答案： B10．已知sin ⎝⎛⎭⎫π4＋α＝32，则sin ⎝⎛⎭⎫3π4－α的值为( ) A.12 B ．－12C.32D ．－32解析： ∵⎝⎛⎭⎫π4＋α＋⎝⎛⎭⎫3π4－α＝π， ∴3π4－α＝π－⎝⎛⎭⎫π4＋α， ∴sin ⎝⎛⎭⎫3π4－α＝sin ⎣⎡⎦⎤π－⎝⎛⎭⎫π4＋α＝sin ⎝⎛⎭⎫π4＋α＝32.答案： C11．当x ＝π4时，函数f (x )＝A sin(x ＋φ)(A ＞0)取得最小值，则函数y ＝f ⎝⎛⎭⎫3π4－x 是( ) A ．奇函数且图象关于点⎝⎛⎭⎫π2，0对称 B ．偶函数且图象关于点(π，0)对称 C ．奇函数且图象关于直线x ＝π2对称D ．偶函数且图象关于点⎝⎛⎭⎫π2，0对称解析： 当x ＝π4时，函数f (x )＝A sin(x ＋φ)(A ＞0)取得最小值，即π4＋φ＝－π2＋2k π(k ∈Z )，即φ＝－3π4＋2k π(k ∈Z )，所以f (x )＝A sin ⎝⎛⎭⎫x －3π4(A ＞0)，所以y ＝f ⎝⎛⎭⎫3π4－x ＝A sin ⎝⎛⎭⎫3π4－x －3π4＝－A sin x ，所以函数y ＝f ⎝⎛⎭⎫3π4－x 为奇函数且图象关于直线x ＝π2对称，故选C. 答案： C12．函数f (x )＝3sin ⎝⎛⎭⎫2x －π3的图象为C . ①图象C 关于直线x ＝1112π对称；②函数f (x )在区间⎝⎛⎭⎫－π12，5π12内是增函数； ③由y ＝3sin 2x 的图象向右平移π3个单位长度可以得到图象C .以上三个论断中，正确论断的个数是( ) A ．0 B ．1 C ．2D ．3解析： ①f ⎝⎛⎭⎫11π12＝3sin ⎝⎛⎭⎫116π－π3＝3sin 32π＝－3， ∴直线x ＝1112π为图象C 的对称轴，①正确；②令2x －π3∈⎣⎡⎦⎤2k π－π2，2k π＋π2(k ∈Z )， 解得x ∈⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z )． 令k ＝0，得⎝⎛⎭⎫－π12，5π12为函数f (x )的一个增区间， ∴②正确；③将y ＝3sin 2x 的图象向右平移π3个单位长度，则有y ＝3sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π3＝3sin ⎝⎛⎭⎫2x －2π3，∴③错误．答案： C二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上) 13．设x ∈(0，π)，则f (x )＝cos 2x ＋sin x 的最大值是________． 解析： ∵f (x )＝cos 2x ＋sin x ＝－sin 2x ＋sin x ＋1 ＝－⎝⎛⎭⎫sin x －122＋54， 又x ∈(0，π)，∴0＜sin x ≤1， ∴当sin x ＝12时，f (x )的最大值是54.答案： 5414．国际油价在某一时间内呈现正弦波动规律：P ＝A sin ⎝⎛⎭⎫ωπt ＋π4＋60(美元)(t (天)，A >0，ω>0)，现采集到下列信息：最高油价80美元，当t ＝150(天)时达到最低油价，则ω的最小值为__________．解析： 因为A sin ⎝⎛⎭⎫ωπt ＋π4＋60＝80， sin ⎝⎛⎭⎫ωπt ＋π4≤1， 所以A ＝20，当t ＝150(天)时达到最低油价， 即sin ⎝⎛⎭⎫150ωπ＋π4＝－1， 此时150ωπ＋π4＝2k π－π2，k ∈Z ，因为ω>0，所以当k ＝1时，ω取最小值， 所以150ωπ＋π4＝32π，解得ω＝1120.答案：112015．设函数f (x )＝sin(ωx ＋φ)，A ＞0，ω＞0，若f (x )在区间⎣⎡⎦⎤π6，π2上具有单调性，且f ⎝⎛⎭⎫π2＝f ⎝⎛⎭⎫2π3＝f ⎝⎛⎭⎫π6，则f (x )的最小正周期为________．解析： 由f (x )在区间⎣⎡⎦⎤π6，π2上具有单调性，且f ⎝⎛⎭⎫π2＝f ⎝⎛⎭⎫π6知，f (x )有对称中心⎝⎛⎭⎫π3，0，由f ⎝⎛⎭⎫π2＝f ⎝⎛⎭⎫2π3知，f (x )有对称轴x ＝12⎝⎛⎭⎫π2＋2π3＝7π12，记T 为最小正周期，则T 2≥π2－π6⇒T ≥2π3，从而7π12－π3＝π4，故T ＝π. 答案： π16．某时钟的秒针端点A 到中心点O 的距离为5 cm ，秒针均匀地绕点O 旋转，当时间t ＝0时，点A 与钟面上标12的点B 重合，若将A ，B 两点的距离d (cm)表示成时间t (s)的函数，则d ＝________，其中t ∈[0,60]．解析： 秒针1 s 转π30弧度，t s 后秒针转了π30t 弧度，如图所示sin πt 60＝d25，所以d ＝10 sinπt60. 答案： 10sinπt 60三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知角α的终边经过单位圆上的点P ⎝⎛⎭⎫45，－35. (1)求sin α的值； (2)求cos (2π－α)sin (π＋α)·tan (π＋α)cos (3π－α)的值．解析： (1)∵点P 在单位圆上， ∴由正弦的定义得sin α＝－35.(2)原式＝cos α－sin α·tan α－cos α＝sin αsin α·cos α＝1cos α，由余弦的定义得cos α＝45，故所求式子的值为54.18．(本小题满分12分)已知函数f (x )＝tan ⎝⎛⎭⎫π2x ＋π3. (1)求f (x )的最小正周期； (2)求f (x )的定义域和单调区间； 解析： (1)对于函数f (x )＝tan ⎝⎛⎭⎫π2x ＋π3，它的最小正周期等于T ＝ππ2＝2.(2)令π2x ＋π3≠k π＋π2，得x ≠2k ＋13，k ∈Z ，故函数的定义域为⎩⎨⎧⎭⎬⎫x | x ≠2k ＋13，k ∈Z ；令k π－π2＜π2x ＋π3＜k π＋π2，得2k －53＜x ＜2k ＋13.所以函数f (x )的单调增区间为⎝⎛⎭⎫2k －53，2k ＋13，k ∈Z . 19．(本小题满分12分)设函数f (x )＝3sin ⎝⎛⎭⎫ωx ＋π6，ω＞0且以π2为最小正周期． (1)求f (0)； (2)求f (x )的解析式；(3)已知f ⎝⎛⎭⎫π12＋α4＝95，求sin α的值． 解析： (1)f (0)＝3sin π6＝32.(2)因为f (x )＝3sin ⎝⎛⎭⎫ωx ＋π6且π2为最小正周期， 所以2πω＝π2，ω＝4，f (x )＝3sin ⎝⎛⎭⎫4x ＋π6. (3)f (x )＝3sin ⎝⎛⎭⎫4x ＋π6， ∴f ⎝⎛⎭⎫π12＋α4＝3sin ⎝⎛⎭⎫α＋π3＋π6＝3cos α， 即3cos α＝95，∴cos α＝35，∴sin α＝±45.20．(本小题满分12分)已知函数f (x )＝sin(x ＋φ)，其中0＜φ＜π，x ∈R ，其图象经过点M ⎝⎛⎭⎫π3，12.(1)求f (x )的解析式；(2)作出函数y ＝1－2f (x )在[0,2π]内的简图，并指出函数y ＝1－2f (x )在[0,2π]内的单调递减区间．解析： (1)∵函数f (x )的图象经过点M ⎝⎛⎭⎫π3，12，∴sin ⎝⎛⎭⎫π3＋φ＝12， ∵0＜φ＜π，∴φ＝π2，∴f (x )＝sin ⎝⎛⎭⎫x ＋π2＝cos x . (2)按五个关键点列表：x 0 π2 π 3π2 2π 1－2cos x－1131－1描点并将它们用光滑的曲线连接起来，如图所示，由图象可知函数y ＝1－2f (x )在[0,2π]内的单调递减区间为[π，2π]．21．(本小题满分12分)函数f 1(x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A ＞0，ω＞0，|φ|＜π2的一段图象过点(0,1)，如图所示．(1)求函数f 1(x )的解析式；(2)将函数y ＝f 1(x )的图象向右平移π4个单位，得到函数y ＝f 2(x )的图象，求y ＝f 2(x )的最大值，并求出此时自变量x 的取值．解析： (1)由题图知，T ＝1112π－⎝⎛⎭⎫－π12＝π， 于是ω＝2πT＝2.将y ＝A sin 2x 的图象向左平移π12个单位，得y ＝A sin(2x ＋φ)的图象，于是φ＝2×π12＝π6.将(0,1)代入y ＝A sin ⎝⎛⎭⎫2x ＋π6，得A ＝2. 故f 1(x )＝2sin ⎝⎛⎭⎫2x ＋π6.(2)依题意知，f 2(x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4＋π6＝－2cos ⎝⎛⎭⎫2x ＋π6， 当2x ＋π6＝2k π＋π(k ∈Z )，即x ＝k π＋5π12(k ∈Z )时，y max ＝2.此时x 的取值为⎩⎨⎧⎭⎬⎫x | x ＝k π＋5π12，k ∈Z .22．(本小题满分12分)“海之旅”表演队在一海滨区域进行集训，该海滨区域的海浪高度y (米)随着时刻t (0≤t ≤24)而周期性变化．为了了解变化规律，该队观察若干天后，得到每天各时刻t 的浪高数据的平均值如下表：t 0 3 6 9 12 15 18 21 24 y1.01.41.00.61.01.40.90.61.0(1)从y ＝ax ＋b ，y ＝A sin(ωx ＋φ)＋b ⎝⎛⎭⎫A ＞0，ω＞0，|φ|＜π2中选择一个合适的函数模型，并求出函数解析式；(2)如果确定当浪高不低于0.8米时才进行训练，试安排白天内恰当的训练时间段． 解析： (1)作出y 关于t 的变化图象如下图所示，由图，可知选择y ＝A sin(ωx ＋φ)＋b 函数模型较为合适．由图可知A ＝1.4－0.62＝25，T ＝12，b ＝1.4＋0.62＝1，则ω＝2π12＝π6，y ＝25sin ⎝⎛⎭⎫π6t ＋φ＋1. 由t ＝0时，y ＝1， 得π6×0＋φ＝2k π，k ∈Z ， 所以φ＝2k π，k ∈Z ， 又|φ|＜π2，所以φ＝0，所以y ＝25sin π6t ＋1(0≤t ≤24)．(2)由y ＝25sin π6t ＋1≥45(0≤t ≤24)，得sin π6t ≥－12，则－π6＋2k π≤π6t ≤7π6＋2k π，k ∈Z ，得－1＋12k ≤t ≤7＋12k ，k ∈Z . 从而0≤t ≤7或11≤t ≤19或23≤t ≤24. 所以在白天11时～19时进行训练较为恰当．莘莘学子，最重要的就是不要去看远方模糊的，而要做手边清楚的事。

单元质量评估(120 分钟150 分)一、选择题 ( 本大题共 12 小题 , 每题 5 分, 共 60 分, 在每题给出的四个选项中 , 只有一项为哪一项切合题目要求的 )1.扇形的周长是 4, 面积为 1, 则该扇形的圆心角的弧度数是( C )A. B.1 C.2 D.42. 若 120°角的终边上有一点 (-4,a),则 a 的值为( C )A.-4B. ±4C.4D.23. 以下三角函数值的符号判断正确的选项是( C )A.sin 156°<0B.cos>0C.tan<0D.tan556°<04.sin 300°+tan 600°的值等于 ( B )A.-B.C.- +D.+5. 已知函数 f(x)=3sin x-4cos x(x∈R)的一个对称中心是(x0,0),则tan x 0的值为 ( D )A.-B.C.-D.6.以下函数中 , 最小正周期为π, 且图象对于直线 x= 对称的是( B )A.y=sinB.y=sinC.y=cosD.y=cos7.函数 f(x)=Asinx(A>0) 的图象如下图 ,P,Q 分别为图象的最高点和最低点 ,O 为坐标原点 , 若 OP⊥OQ,则 A= ( B )A.3B.C.D.18.函数 y=sin的图象可由函数y=cos x的图象起码向右平移m(m>0)个单位长度获得 , 则 m= ( A )A.1B.C.D.9. 函数 f(x)=2sin(ωx+φ)的部分图象如下图,则ω,φ的值分别是( B )A.2,-B.2,-C.4,D.4,10. 函数 y=cos2x+sin x-1的值域为( C )A. B.C. D.[-2,0]11. 已知函数 f(x)=tanωx在内是减函数,则实数ω 的取值范围是( B )A.(0,1]B.[-1,0)C.[-2,0)D.12. 已知函数 f(x)=sin(ωx+φ),x=-为f(x)的零点, x= 为 y=f(x) 图象的对称轴 , 且 f(x) 在单一,则ω 的最大值为( B )A.11B.9C.7D.5二、填空题 ( 本大题共 4 小题 , 每题 5 分, 共 20 分, 将答案填在题中的横线上 )13. 若 2sinα-cosα=0,则=- .14. 函数 f(x)= sin+cos的最大值为.15. 设函数 f(x)=cos x, 先将 f(x) 纵坐标不变 , 横坐标变成本来的 2 倍,再将图象向右平移个单位长度后得g(x), 则函数 g(x) 到原点距离最近的对称中心为.16.给出以下命题 :①存在实数 x, 使 sin x+cos x=;②函数 y=sin是偶函数;③若α, β是第一象限角 , 且α>β, 则 cos α<cos β;④函数 y=sin 2x 的图象向左平移个单位,获得函数y=sin的图象 .此中结论正确的序号是②.( 把正确的序号都填上 )三、解答题 ( 本大题共 6 小题 , 共 70 分. 解答时应写出文字说明 , 证明过程或演算步骤 )17.( 本小题满分 10 分) 已知 tan α+= , 求2sin 2(3 π- α)-3cos·sin+2 的值 .【分析】由于 tanα+= ,因此 2tan 2α-5tanα+2=0.解得 tanα=或tanα=2.2sin 2 (3 π- α)-3cos sin+2=2sin 2α-3sin αcos α+2=+2 =+2.当 tanα=时,原式=+2=- +2= ;当 tan α=2 时,原式 =+2= +2=.18.( 本小题满分 12 分) 已知f( α)=.(1) 化简 f( α).(2) 当α=-时,求f(α)的值.【分析】 (1)f( α)===-cosα.(2) 当α=-时,f(α)=-cos=-cos =- .19.( 本小题满分 12 分)(1) 已知 x 是第三象限的角 , 化简三角式-.(2) 已知 tan θ=(0<a<1). 求证 :+=-2.【分析】 (1) 由于 x 是第三象限的角 ,因此-=-=-=-=-2tan x.(2) 由于 tanθ=,因此==-1, 因此 a=cos 2θ,因此+=====-2, 故原式建立 .20.( 本小题满分 12 分) 已知函数f(x)=Asin( ωx+φ)的部分图象如下图.(1)求 f(x) 的分析式 .(2)求 f(x) 在上的最大、最小值及相应的x的值.【分析】 (1) 由图象可知 ,A=2.由于周期 T== π,因此= π,ω>0, 解得ω =2.因此 f(x)=2sin(2x+φ).代入点,得 sin=1,因此+ φ= +2k π,k ∈Z, 即φ=-+2k π,k ∈Z.又| φ|< ,因此φ=- .因此 f(x)=2sin.(2) 由于 x ∈,因此 2x-∈.因此当 2x- = ,即 x=时,f(x)max=2;当 2x- =-或,即 x=0 或时,f(x)min=-.21.( 本小题满分 12 分) 平潭国际“花式风筝冲浪”集训队 , 在平潭龙凤头海滨浴场进行集训, 海滨地区的某个观察点观察到该处水深y( 米) 跟着一天的时间 t(0 ≤t ≤24, 单位 : 时) 呈周期性变化 , 某天各时辰 t 的水深数据的近似值如表 :t( 时)036912 15 18 21 24y( 米) 1.5 2.4 1.5 0.6 1.4 2.4 1.6 0.61.5(1)依据表中近似数据画出散点图 . 察看散点图 , 从①y=Asin( ωt+ φ), ②y=Acos(ωt+ φ)+b, ③y=-Asinωt+b(A>0, ω>0, - π<φ<0)中选择一个适合的函数模型, 并求出该拟合模型的函数分析式 .(2)为保证队员安全 , 规定在一天中的 5～18 时且水深不低于 1.05 米的时候进行训练 , 依据 (1) 中的选择的函数分析式 , 试问 : 这天能够安排什么时间段组织训练 , 才能保证集训队员的安全 .【分析】 (1) 依据表中近似数据画出散点图,如下图 :依题意 ,选② y=Acos(ωt+φ)+b做为函数模型,因此 A==0.9,b==1.5.由于 T==12, 因此ω= .因此 y=0.9cos+1.5.又由于函数 y=0.9cos+1.5 的图象过点,因此2.4=0.9 ×cos+1.5.因此 cos=1.因此 sinφ=-1.又由于-π<φ<0,因此φ=-.因此 y=0.9cos+1.5=0.9sin t+1.5.(2) 由(1) 知,y=0.9sin t+1.5.令 y ≥1.05, 即 0.9sin t+1.5 ≥1.05.因此 sin t ≥- .因此 2k π-≤ t≤2kπ+(k ∈Z).因此 12k-1 ≤t ≤12k+7(k∈Z).又由于 5 ≤t ≤18, 因此 5 ≤t ≤7 或 11 ≤t ≤18.因此这天能够安排清晨 5 点至 7 点以及 11 点至 18 点的时间段组织训练 ,才能保证集训队员的安全 .22.( 本小题满分 12 分) 已知函数 f(x)=sin(ωx+φ)的部分图象如下图 .(1)求函数 f(x) 的分析式 , 并求出 f(x) 的单一递加区间 .(2) 将函数 f(x) 的图象上各个点的横坐标扩大到本来的 2 倍, 再将图象向右平移个单位,获得g(x)的图象,若存在x∈使得等式3g(x)+1=2[a+g 2(x)] 建立 , 务实数 a 的取值范围 .【分析】(1) 设函数 f(x) 的周期为 T,由图象可知=- =.因此 T= π,即= π,又ω>0, 解得ω =2.因此 f(x)=sin(2x+φ).由于点在函数 f(x) 的图象上 ,因此 sin=1, 即+ φ=+2k π,k ∈Z,解得φ=+2k π,k ∈Z.又由于 | φ|< ,因此φ= .因此 f(x)=sin.令- +2k π≤2x+≤ +2kπ(k∈Z),解得 -+k π≤x ≤ +k π(k ∈Z),因此 f(x) 的单一递加区间为(k ∈Z).-11-(2) 经过图象变换 ,获得函数 g(x)=f=sin x.于是问题即为“存在x ∈,使得等式 3sin x+1=2(a+sin2x)成立” .即 2a=-2sin 2 x+3sin x+1在x∈上有解.令 t=sin x∈[0,1],则2a=-2t 2 +3t+1在t∈[0,1]上有解,由于 -2t 2 +3t+1=-2+∈,因此 2a ∈,即实数 a 的取值范围为.封闭 Word 文档返回原板块-12-。

第一章单元质量测评对应学生用书P43 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题,共60分)一、选择题（本大题共１2小题，每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)１.ｓin-错误!的值等于( ）Ａ.＼ｆ（１，２) Ｂ．-错误!Ｃ.错误!未定义书签。

D．－错误!未定义书签。

答案 A解析ｓin-＼f（1９π，6)＝－ｓin错误!未定义书签。

＝-sin错误!未定义书签。

＝ｓｉn 错误!＝错误!.2．已知扇形的半径为r,周长为3r,则扇形的圆心角等于( )A.错误!B.１ C．错误! D.3答案B解析弧长l=3r-2ｒ＝r,则圆心角＝错误!=1.3．若cos(-１0０°)=ａ，则tan８０°=( ）Ａ.－错误!未定义书签。

B.错误!Ｃ．-错误!Ｄ．错误!答案A解析∵cos(-100°）=cos１０0°＝cos(18０°－80°）＝-cos８0°=a,∴cos８0°=-ａ．又∵sｉn２80°+coｓ28０°=１,siｎ８0°>0，∴siｎ80°＝错误!未定义书签。

=ﻬ错误!未定义书签。

＝错误!未定义书签。

,故tan８0°＝错误!=-错误!.4．设0≤α〈２π，若sinα＞3cosα，则α的取值范围是( )A.错误!B.错误!∪错误!C．错误!∪错误!未定义书签。

D．错误!答案D解析当α∈错误!时,coｓα>0,由ｓinα〉错误!coｓα，得tａnα>错误!，解得α∈错误!未定义书签。

；当α∈错误!时,sｉnα≥0，cｏsα≤0,显然原式成立;当α∈错误!时,ｃosα〈0，易得taｎα<错误!未定义书签。

,解得α∈错误!未定义书签。

；当α∈错误!时，sinα〈0，cｏsα≥0,显然原式不成立.综上，α的取值范围是错误!未定义书签。

第一章三角函数(120分钟150分)一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.与-525°终边相同的角可表示为( )A.525°-k·360°(k∈Z)B.165°+k·360°(k∈Z)C.195°+k·360°(k∈Z)D.-195°+k·360°(k∈Z)【解析】选C.-525°=-360°×2+195°，所以-525°与195°终边相同，所以与-525°终边相同的角可表示为195°+k·360°(k∈Z).2.若点P在的终边上，且|OP|=2，则点P的坐标为( )A.(1，-)B.(，-1)C.(-1，-)D.(-1，)【解析】选A.由任意角的三角函数定义知x P=|OP|cos=2×=1，y P=|OP|sin=2×=-，故点P坐标为(1，-).【补偿训练】若点A(x，y)是240°角终边上异于原点的一点，则的值为( )A.-B.C.-D.【解析】选D.由题意知=tan240°=tan(180°+60°)=tan60°=.3.(2015·合肥高一检测)已知tanα>0，且sinα+cosα<0，则( )A.cosα>0B.cosα<0C.cosα=0D.cosα符号不确定【解析】选B.由tanα>0知α是第一或第三象限角.又因为sinα+cosα<0，所以α是第三象限角，所以cosα<0.4.把函数y=sinx(x∈R)的图象上所有的点向左平行移动个单位长度，再将所得的图象的横坐标缩短到原来的倍(纵坐标不变)，得到的图象所表示的函数是( )A.y=sin，x∈RB.y=sin，x∈RC.y=sin，x∈RD.y=sin，x∈R【解析】选D.把函数y=sinx(x∈R)的图象上所有的点向左平移个单位长度，得到y=sin的图象，再将所得的图象的横坐标缩短到原来的倍(纵坐标不变)，得到y=sin的图象.5.在同一个坐标系中画出函数y=a x，y=sinax的部分图象，其中a>0且a≠1，则下列所给图象中可能正确的是( )【解析】选D.当0<a<1时，y=sinax的周期T=>2π，B不正确，D正确；当a>1时，y=sinax的周期T=<2π.A，C都不正确.【补偿训练】不等式l og a x>sin2x(a>0且a≠1)对任意x∈都成立，则a的取值范围为( )A. B.C.∪D.【解题指南】先分析临界位置，如l og a x过点，再确定范围.【解析】选D.当y=log a x的图象恰好过点时有log a=1，所以a=.结合图形知≤a<1时在上y=log a x总在y=sin2x上方.即log a x>sin2x成立.6.下列函数中，对于任意x∈R，同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )A.f(x)=sinxB.f(x)=sinx·cosxC.f(x)=cosxD.f(x)=cos2x【解析】选D.由f(x)=f(-x)知f(x)为偶函数，排除A，B.由f(x-π)=f(x)知x=是f(x)图象的一条对称轴，排除C，故选D.7.(2015·汕头高一检测)下列比较大小错误的是( )A.sin(-70°)>sin(-80°)B.cos>cosC.tan<tanD.tan38°<tan43°【解析】选C.-90°<-80°<-70°<0°且y=sinx在上为增函数，所以sin(-80°)<sin(-70°)，故A正确；cos=cos=cos>0，cos=cos=cos<0，所以cos>cos，故B正确；tan=tan=-tan=-，tan=tan=-tan=-，所以tan>tan，C错误，易知D正确.8.已知函数f(x)=Atan(ωx+φ)，y=f(x)的部分图象如图，则f=( )A.3B.C.1D.【解析】选A.由题干图知，T=2×=，所以ω==2.又图象过点，所以Atan=0，所以tan=0，所以φ+=kπ，k∈Z.所以φ=kπ-，k∈Z.又|φ|<，所以φ=，所以f(x)=Atan.又图象过点(0，1)，所以Atan=1，所以A=，即f(x)=tan，所以f=tan=3.【补偿训练】已知函数f(x)=Asin(ωx+φ)(A>0，ω>0，|φ|<)的部分图象如图所示，当x∈时，满足f(x)=1的x的值为( )A. B. C. D.【解析】选B.由图象知A=2.=2×=π，ω=2.故f(x)=2sin(2x+φ)，x=-时y=0，代入上式，得0=2sin，所以-+φ=kπ，k∈Z，故φ=kπ+，k∈Z，又|φ|<，所以φ=，所以f(x)=2sin.由f(x)=1得sin=，又2x+∈，所以2x+=，所以x=.9.(2015·安徽高考)已知函数f(x)=Asin(ωx+φ)(A，ω，φ均为正的常数)的最小正周期为π，当x=时，函数f(x)取得最小值，则下列结论正确的是( )A.f<f<fB.f<f<fC.f<f<fD.f<f<f【解析】选A.因为函数f=Asin(A，ω，φ均为正的常数)的最小正周期为π，所以T==π⇒ω=2，所以f=Asin，当x=时，2×+φ=+2kπ，k∈N⇒φ=+2kπ，k∈N，所以f=Asin，当2x+=+2kπ，k∈Z，即x=+kπ，k∈Z时函数f取得最大值.下面只需要判断2，-2，0与最近的最高点处对称轴的距离，距离越大，函数值越小.当k=0时，x=，≈0.52，≈1.48；当k=1时，x=，≈1.67；当k=-1时，x=-，≈0.62，所以f<f<f，故选A.【补偿训练】(2015·宜昌高一检测)设y=f(t)是某港口水的深度关于时间t(时)的函数，其中0≤t≤24，下表是该港口某一天从0至24时记录的时间t与水深y的关系.经长期观察，函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.根据上述数据，函数y=f(t)的解析式为( )A.y=12+3sin，t∈[0，24]B.y=12+3sin，t∈[0，24]C.y=12+3sin，t∈[0，24]D.y=12+3sin，t∈[0，24]【解析】选A.由已知得A==3，k==12.=15-3，所以ω=，所以y=12+3sin，t=3，y=15代入上式得sin=1，解得φ=2kπ，k∈Z.所以y=12+3sin，t∈[0，24].10.(2015·武汉高一检测)函数f(x)=asinx+blog2(x+)+4(a，b为常数)，若f(x)在(0，+∞)上有最小值-4，则f(x)在(-∞，0)上有( )A.最大值-2B.最大值4C.最大值10D.最大值12【解析】选D.设g(x)=f(x)-4，则g(x)为奇函数.因为f(x)在(0，+∞)上有最小值-4，所以g(x)在(0，+∞)上有最小值-8.又因为g(x)为奇函数，所以g(x)在(-∞，0)上有最大值8.所以f(x)在(-∞，0)上有最大值12.11.定义在R上的函数满足f(x+2)=f(x)，且x∈[1，3]时，f(x)=cos x，则下列大小关系正确的是( )A.f(tan1)>fB.f<fC.f(sin2)>f(cos2)D.f(cos1)>f(sin1)【解析】选C.由题意知函数f(x)是以2为周期的函数，且在区间[-1，0]上为减函数，在区间[0，1]上是增函数，x=1是函数f(x)的一条对称轴，于是f(cos2)=f(2-cos2)=f(-cos2)，又因<2<，所以1>sin2>-cos2>0，因此有f(sin2)>f(-cos2)=f(cos2).12.(2015·厦门高一检测)已知函数f(x)=sinx+x，则使不等式f(sinθ)+f(cosθ)≥0成立的θ的取值范围是( )A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)【解析】选C.函数f(x)=sinx+x的定义域为R，因为f(-x)=sin(-x)+(-x)=-sinx-x=-(sinx+x)=-f(x)，所以f(x)是奇函数，不等式f(sinθ)+f(cosθ)≥0可化为f(sinθ)≥-f(cosθ)=f(-cosθ)，又因为y=sinx和y=x在[-1，1]上均为增函数，所以f(x)=sinx+x在[-1，1]上为增函数，且sinθ∈[-1，1]，-cosθ∈[-1，1]，所以sinθ≥-cosθ，即sinθ+cosθ≥0，角θ终边所在区域如图所示，所以θ∈(k∈Z).二、填空题(本大题共4小题，每小题5分，共20分.请把正确答案填在题中横线上)13.弧长为3π，圆心角为的扇形的面积为________.【解析】设扇形的半径为R，由已知得·R=3π，所以R=4.所以扇形的面积S=××42=6π.答案：6π14.(2015·黄冈高一检测)函数y=2sin，x∈[-π，0]的单调递增区间为__________. 【解析】y=2sin=-2sin，由2kπ+≤2x-≤2kπ+，k∈Z，得kπ+≤x≤kπ+，k∈Z，设A=，B=[-π，0]，A∩B=，所以y=2sin，x∈[-π，0]的单调递增区间为[-，-]答案：【补偿训练】若f(x)=2sinωx(ω>0)在区间上的最大值是，则ω=__________.【解析】f(x)=2sinωx在即上为增函数.由题意知且f=.所以所以ω=6k+或6k+且0<ω<，所以ω=.答案：15.(2015·南昌高一检测)如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系式y=Asin(ωx+φ)+2(A>0，ω>0，φ∈(-，))，且初始位置(即x=0)时y=，则函数的表达式为__________.【解析】函数表达式为y=Asin(ωx+φ)+2，则由题意得A=3；T==15，故ω==π；由初始位置时y=知，=3sinφ+2；故sinφ=；再由φ∈知，φ=，所以函数表达式为y=3sin+2.答案：y=3sin+216.给出下列4个命题：①函数y=的最小正周期是；②直线x=是函数y=2sin的一条对称轴；③若sinα+cosα=-，且α为第二象限角，则tanα=-；④函数y=cos(2-3x)在区间上单调递减.其中正确的是__________.(写出所有正确命题的序号).【解析】函数y=sin的最小正周期是π，故①正确.对于②，当x=π时，2sin=2sinπ=-2，故②正确.对于③，由(sinα+cosα)2=得2sinαcosα=-，因为α为第二象限角，所以sinα-cosα==，所以sinα=，cosα=-，所以tanα=-，故③正确.对于④，函数y=cos(2-3x)的最小正周期为，而区间长度>，显然④错误.答案：①②③三、解答题(本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)若cosα=，α是第四象限角，求的值.【解析】由已知得sinα=-，===-=.18.(12分)(1)已知角α的顶点在原点，始边与x轴的非负半轴重合，终边经过点P(-3，4)，求cos(π-α)+cos的值.(2)若tanβ=3，求的值.【解析】(1)r=|OP|==5.所以sinα==，cosα==-，所以cos(π-α)+cos=-cosα-sinα=--=-.(2)原式===.19.(12分)(2015·宜昌高一检测)已知函数f(x)=2sin(2ωx+)+1(其中0<ω<1)，若点是函数f(x)图象的一个对称中心，(1)试求ω的值.(2)先列表，再作出函数f(x)在区间x∈[-π，π]上的图象.【解析】(1)因为点是函数f(x)图象的一个对称中心，所以-+=kπ，k∈Z，所以ω=-3k+，k∈Z，因为0<ω<1，所以k=0，ω=.(2)由(1)知f(x)=2sin+1，x∈[-π，π]列表如下，-ππ则函数f(x)在区间x∈[-π，π]上的图象如图所示.【拓展延伸】“巧”画图象“妙”解题在利用“五点法”画函数y=Asin(ωx+φ)的图象时，如果能正确利用函数的性质就能更快、更准确地画出函数图象的简图.例如定出第一个关键点后，就可以根据五个关键点横坐标之间的距离都为，画出另外四个关键点.20.(12分)(2015·湖北高考)某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时，列表并填入了部分数据，如表：(1)请将上表数据补充完整，并直接写出函数f(x)的解析式.(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度，得到y=g(x)的图象.若y=g(x)图象的一个对称中心为，求θ的最小值.【解析】(1)根据表中已知数据，得A=5，ω=2，φ=-.数据补全如表：π且函数表达式为f(x)=5sin.(2)由(1)知f(x)=5sin，得g(x)=5sin.因为y=sinx的对称中心为(kπ，0)，k∈Z.令2x+2θ-=kπ，k∈Z，解得x=+-θ，k∈Z.由于函数y=g(x)的图象关于点成中心对称，令+-θ=，k∈Z，解得θ=-，k∈Z.由θ>0可知，当k=1时，θ取得最小值.【补偿训练】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时，列表并填入的部分数据如表：(1)请将表数据补全，并直接写出函数f(x)的解析式.(2)将函数f(x)的图象上各点的纵坐标不变，横坐标缩短到原来的，得到函数y=g(x)的图象，求函数y=g(x)的单调递减区间.【解析】(1)函数f(x)的解析式为f(x)=2sin.(2)函数g(x)=2sin.令2kπ+≤2x-≤2kπ+，k∈Z，得kπ+≤x≤kπ+，k∈Z，所以函数y=g(x)的单调递减区间为[kπ+，kπ+]，k∈Z.21.(12分)已知f(x)=3sin-1.(1)f(x)的图象是由y=sinx的图象如何变换而来？(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.【解析】(1)将函数y=sinx图象上每一点的横坐标不变，纵坐标伸长到原来的3倍得到函数y=3sinx的图象，再把所得函数图象上每一点的横坐标缩短为原来的倍(纵坐标不变)，得到函数y=3sin2x的图象，再把所得函数的图象向左平移个单位长度，得到函数y=3sin的图象，再把所得函数的图象向下平移一个单位长度，得到函数f(x)=3sin-1的图象.(2)最小正周期T=π，由2x+=+kπ(k∈Z)，得对称轴方程为x=+(k∈Z).当2x+=+2kπ(k∈Z)，即x=+kπ(k∈Z)时，f(x)取得最大值2.【补偿训练】(2015·都江堰高一检测)已知函数f(x)=Asin(ωx+φ)其中的周期为π，其图象上一个最高点为M，(1)求f(x)的解析式.(2)当x∈时，求f(x)的最值及相应的x的值.【解析】(1)由T=π得ω===2，由最高点为M得A=2，且2sin=2，即sin=1，所以+φ=2kπ+，故φ=2kπ+(k∈Z)，又因为φ∈，所以φ=，所以f(x)=2sin.(2)因为x∈，所以2x+∈，所以当2x+=，即x=0时，f(x)取得最小值1；当2x+=，即x=时，f(x)取得最大值2.22.(12分)(2015·南通高一检测)某休闲农庄有一块长方形鱼塘ABCD，AB=50米，BC=25米，为了便于游客休闲散步，该农庄决定在鱼塘内建3条如图所示的观光走廊OE，EF和OF，考虑到整体规划，要求O是AB的中点，点E在边BC上，点F在边AD上，且∠EOF=90°.(1)设∠BOE=α，试将△OEF的周长l表示成α的函数关系式，并求出此函数的定义域.(2)经核算，三条走廊每米建设费用均为4000元，试问如何设计才能使建设总费用最低并求出最低总费用. 【解析】(1)因为在Rt△BOE中，OB=25，∠B=90°，∠BOE=α，所以OE=.在Rt△AOF中，OA=25，∠A=90°，∠AFO=α，所以OF=.又∠EOF=90°，所以EF===，所以l=OE+OF+EF=++，即l=，当点F在点D时，这时角α最小，求得此时α=；当点E在C点时，这时角α最大，求得此时α=.故此函数的定义域为.(2)由题意知，要求建设总费用最低，只要求△OEF的周长l的最小值即可.由(1)得，l=，α∈，设sinα+cosα=t，则sinα·cosα=，所以l===，由≤α+≤，得≤t≤，所以≤t-1≤-1，从而+1≤≤+1，当α=，即BE=25时，l min=50(+1)，所以当BE=AF=25米时，铺路总费用最低，最低总费用为200000(+1)元.。

章末质量评估(一) 三角函数(时间：120分钟 满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1．下列各对角中，终边相同的是( )． A.32π和2k π－32π(k ∈Z ) B ．－π5和225π C ．－79π和119π D.203π和1229π解析 ∵119π＝2π＋⎝ ⎛⎭⎪⎫－7π9，故－7π9与11π9的终边相同．答案 C2．已知角α的终边与单位圆交于点⎝ ⎛⎭⎪⎫－32，－12，则sin α的值为( )．A ．－32 B ．－12 C.32D ．12解析 由正弦函数的定义，知sin α＝y ＝－12. 答案 B3．sin ⎝ ⎛⎭⎪⎫－196π的值等于( )．A.12 B ．－12 C.32D ．－32解析 sin ⎝ ⎛⎭⎪⎫－196π＝－sin 196π＝－sin 76π＝sin 16π＝12.4．若一圆弧长等于其所在圆的内接正三角形的边长，则其圆心角的弧度数为( )．A.π3 B ．2π3 C. 3D ．2解析 设圆的半径为r ，则其内接正三角形的边长为3r ，即为弧长，利用弧长公式l ＝α·r ，∴3r ＝α·r ，∴α＝ 3. 答案 C5．要想得到函数y ＝sin x 的图象，只需将函数y ＝cos ⎝ ⎛⎭⎪⎫x －π3的图象( )．A ．向右平移π6个单位长度 B ．向右平移π3个单位长度 C ．向左平移π3个单位长度 D ．向左平移π6个单位长度解析 函数y ＝cos ⎝ ⎛⎭⎪⎫x －π3可化为y ＝sin ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫x －π3＝sin ⎝ ⎛⎭⎪⎫x ＋π6.要想得到函数y ＝sin x 的图象，只需将函数y ＝sin ⎝ ⎛⎭⎪⎫x ＋π6的图象向右平移π6个单位长度．答案 A6．函数y ＝2tan ⎝ ⎛⎭⎪⎫3x －π4的一个对称中心是( )．A.⎝ ⎛⎭⎪⎫π3，0 B ．⎝ ⎛⎭⎪⎫π6，0C.⎝ ⎛⎭⎪⎫－π4，0 D ．⎝ ⎛⎭⎪⎫－π2，0解析 由题意得3x －π4＝k π2(k ∈Z )，解得x ＝(2k ＋1)π12(k ∈Z )．当取k ＝－2，x ＝－π4.即选项C 正确．7．(2012·云南检测)下列各函数值中符号为负的是( )． A ．sin(－1 000°)B ．cos(－2 200°)C ．tan(－10)D ．sin 7π10cos πtan 17π9解析 sin(－1 000°)＝sin 80°>0； cos(－2 200°)＝cos(－40°)＝cos 40°>0； tan(－10)＝tan(3π－10)<0； sin 7π10cos πtan 17π9＝－sin 7π10tan 17π9，sin 7π10>0， tan 17π9<0，故sin 7π10cos πtan 17π9>0.故选C. 答案 C8．已知f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋π2，g (x )＝cos ⎝ ⎛⎭⎪⎫x －π2，则f (x )的图象( )．A ．与g (x )的图象相同B ．与g (x )的图象关于y 轴对称C ．向左平移π2个单位，得g (x )的图象 D ．向右平移π2个单位，得g (x )的图象解析 因为f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋π2＝cos x ，故将其图象向右平移π2个单位，得y ＝g (x )＝cos ⎝ ⎛⎭⎪⎫x －π2的图象．答案 D9．如图所示是y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象的一段，它的一个解析式为( )．A ．y ＝23sin ⎝ ⎛⎭⎪⎫2x ＋π3B ．y ＝23sin ⎝ ⎛⎭⎪⎫x 2＋π4C ．y ＝23sin ⎝ ⎛⎭⎪⎫x －π3D ．y ＝23sin ⎝ ⎛⎭⎪⎫2x ＋23π 解析 由图象可知，A ＝23，T ＝5π12－⎝ ⎛⎭⎪⎫－7π12＝π，∴ω＝2πT ＝2，∴y ＝23sin(2x ＋φ)，将点⎝ ⎛⎭⎪⎫－π12，23代入，得23＝23sin ⎝ ⎛⎭⎪⎫－π6＋φ，φ－π6＝π2，∴φ＝2π3， ∴y ＝23sin ⎝ ⎛⎭⎪⎫2x ＋2π3，故选D. 答案 D10．函数y ＝tan(sin x )的值域为( )． A.⎣⎢⎡⎦⎥⎤－π4，π4 B ．⎣⎢⎡⎦⎥⎤－22，22C ．[－tan 1，tan 1]D ．以上均不对解析 ∵－1≤sin x ≤1，∴sin x ∈⎝ ⎛⎭⎪⎫－π2，π2.又∵y ＝tan x 在⎝ ⎛⎭⎪⎫－π2，π2上单调递增，∴tan (－1)≤y ≤tan 1，即y ∈[－tan 1，tan 1]． 答案 C11．(2012·潍坊检测)为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针位置P (x ，y )．若初始位置为P 0⎝ ⎛⎭⎪⎫32，12，当秒针从P 0(注：此时t ＝0)开始走时，点P 的纵坐标y 与时间t 的函数解析式为( )．A ．y ＝sin ⎝ ⎛⎭⎪⎫π30t ＋π6B ．y ＝sin ⎝ ⎛⎭⎪⎫－π60t －π6C ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6D ．y ＝sin ⎝ ⎛⎭⎪⎫－π30t －π3解析 由题意知，函数的周期为T ＝60，∴ω＝2π60＝π30. 设函数解析式为y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋φ.∵初始位置为P 0⎝ ⎛⎭⎪⎫32，12，∴t ＝0时，y ＝12，∴sin φ＝12，∴φ可取π6，∴函数解析式为y ＝sin ⎝ ⎛⎭⎪⎫－π30t ＋π6.故选C.答案 C12．已知函数y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x －π6，以下说法正确的是( )．A ．周期为π4 B ．偶函数C ．函数图象的一条对称轴为直线x ＝π3 D ．函数在⎣⎢⎡⎦⎥⎤2π3，5π6上为减函数解析 该函数的周期T ＝π2；因为f (－x )＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫－2x －π6＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x ＋π6，因此它是非奇非偶函数；函数y＝sin ⎝ ⎛⎭⎪⎫2x －π6在⎣⎢⎡⎦⎥⎤2π3，5π6上是减函数，但y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x －π6在⎣⎢⎡⎦⎥⎤2π3，5π6上是增函数，因此只有C 正确． 答案 C二、填空题(本大题共4小题，每小题5分，共20分．请把正确的答案填在题中的横线上)13．(2012·广州期末)已知sin α＝35，cos α＝－45，则角α的终边在第________象限．解析 由sin α＝35>0，得角α的终边在第一、二象限；由cos α＝－45<0，得角α的终边在第二、三象限，故角α的终边在第二象限． 答案 二14．已知f (x )＝ax 3＋b sin x ＋1且f (1)＝5，f (－1)的值为________． 解析 ∵f (1)＝5，∴a ＋b sin 1＝4， ∴－a －b ·sin 1＝－4，∴f (－1)＝－a －b ·sin 1＋1＝－3. 答案 －315．已知函数f (x )＝3sin πx k 的图象上相邻的一个最大值点与一个最小值点恰好在圆x 2＋y 2＝k 2上，则f (x )的最小正周期为________． 解析 T ＝2π⎪⎪⎪⎪⎪⎪πk ＝2|k |.由题意知⎝ ⎛⎭⎪⎫|k |2，3在圆上，∴|k |24＋3＝k 2，∴|k |＝2，∴T ＝4. 答案 4 16．有下列说法：①函数y ＝－cos 2x 的最小正周期是π；②终边在y 轴上的角的集合是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α＝k π2，k ∈Z；③在同一直角坐标系中，函数y ＝sin x 的图象和函数y＝x 的图象有三个公共点；④把函数y ＝3sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象向右平移π6个单位长度得到函数y ＝3sin 2x 的图象；⑤函数y ＝sin ⎝ ⎛⎭⎪⎫x －π2在[0，π]上是减函数．其中，正确的说法是________．解析 对于①，y ＝－cos 2x 的最小正周期T ＝2π2＝π，故①对；对于②，因为k ＝0时，α＝0，角α的终边在x 轴上，故②错；对于③，作出y ＝sin x 与y ＝x 的图象，可知两个函数只有(0,0)一个交点，故③错；对于④，y ＝3sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象向右平移π6个单位长度后，得y ＝3sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π6＋π3＝3sin 2x ，故④对；对于⑤，y ＝sin ⎝ ⎛⎭⎪⎫x －π2＝－cos x ，在[0，π]上为增函数，故⑤错．答案 ①④三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(本小题满分10分)(1)已知角α的终边经过点P (4，－3)，求2sin α＋cos α的值；(2)已知角α的终边经过点P (4a ，－3a )(a ≠0)，求2sin α＋cos α的值； (3)已知角α终边上一点P 与x 轴的距离与y 轴的距离之比为3∶4，求2sin α＋cos α的值．解 (1)∵r ＝x 2＋y 2＝5，∴sin α＝y r ＝－35，cos α＝x r ＝45，∴2sin α＋cos α＝－65＋45＝－25.(2)∵r ＝x 2＋y 2＝5|a |，∴当a >0时，r ＝5a ，∴sin α＝－3a 5a ＝－35，cos α＝45，∴2sin α＋cos α＝－25；当a <0时，r ＝－5a ，∴sin α＝－3a －5a ＝35，cos α＝－45，∴2sin α＋cos α＝25.(3)当点P 在第一象限时，sin α＝35，cos α＝45，2sin α＋cos α＝2；当点P 在第二象限时，sin α＝35，cos α＝－45，2sin α＋cos α＝25；当点P 在第三象限时，sin α＝－35，cos α＝－45，2sin α＋cos α＝－2；当点P 在第四象限时，sin α＝－35，cos α＝45，2sin α＋cos α＝－25.18．(本小题满分12分)已知tan α＝3，求下列各式的值： (1)3cos (－π－α)－sin (π＋α)3cos ⎝ ⎛⎭⎪⎫π2＋α＋sin ⎝ ⎛⎭⎪⎫3π2－α；(2)2sin 2α－3sin αcos α－1.解 (1)原式＝－3cos α＋sin α－3sin α－cos α＝－3＋tan α－3tan α－1＝3－3－33－1＝6－5313.(2)原式＝2sin 2α－3sin αcos α－sin 2α－cos 2αsin 2α＋cos 2α＝2tan 2α－3tan α－tan 2α－1tan 2α＋1＝18－9－9－19＋1＝－110.19．(本小题满分12分)已知f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋32，x ∈R .(1)求函数f (x )的最小正周期和单调增区间．(2)函数f (x )的图象可以由函数y ＝sin 2x (x ∈R )的图象经过怎样的变换得到？ 解 (1)T ＝2π2＝π，由2k π－π2≤2x ＋π6≤2k π＋π2，k ∈Z 知k π－π3≤x ≤k π＋π6(k ∈Z )．所以所求的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π3，k π＋π6(k ∈Z )．(2)变换情况如下：y ＝sin 2x ――――――――→向左平移π12个单位y ＝sin ⎣⎢⎡⎦⎥⎤2(x ＋π12)―――――→将图象上各点向上平移32个单位y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋32.20．(本小题满分12分)交流电的电压E (单位：V)与时间t (单位：s)的关系可用E ＝2203sin ⎝ ⎛⎭⎪⎫100πt ＋π6来表示，求：(1)开始时电压；(2)电压值重复出现一次的时间间隔；(3)电压的最大值和第一次获得最大值的时间．解 (1)当t ＝0时，E ＝1103，即开始时的电压为110 3 V. (2)T ＝2π100π＝150(s)，即时间间隔为150 s. (3)电压的最大值为220 3 V.当100πt ＋π6＝π2，t ＝1300，即第一次获得最大值的时间为1300 s.21．(本小题满分12分)函数y ＝A sin(ωx ＋φ)⎝ ⎛⎭⎪⎫A >0，ω>0，0≤φ≤π2在x ∈(0,7π)内只取到一个最大值和一个最小值，且当x ＝π时，y max ＝3；当x ＝6π时，y min ＝－3.(1)求此函数的解析式； (2)求此函数的单调递增区间． 解 (1)由题意得A ＝3，12T ＝5π， ∴T ＝10π，∴ω＝2πT ＝15. ∴y ＝3sin ⎝ ⎛⎭⎪⎫15x ＋φ.∵点(π，3)在此函数图象上， ∴3sin ⎝ ⎛⎭⎪⎫π5＋φ＝3.∴π5＋φ＝π2＋2k π，k ∈Z . ∵0≤φ≤π2，∴φ＝3π10.∴y ＝3sin ⎝ ⎛⎭⎪⎫15x ＋3π10.(2)当－π2＋2k π≤15x ＋3π10≤π2＋2k π，即－4π＋10k π≤x ≤π＋10k π时，函数y ＝3sin ⎝ ⎛⎭⎪⎫15x ＋3π10单调递增，所以此函数的单调递增区间为[－4π＋10k π，π＋10k π](k ∈Z )．22．(本小题满分12分)已知函数f (x )＝A sin(ωx ＋φ)⎝ ⎛⎭⎪⎫A >0，ω>0，|φ|<π2在一个周期内的图象如图所示．(1)求函数的解析式；(2)设0<x <π，且方程f (x )＝m 有两个不同的实数根，求实数m 的取值范围以及这两个根的和．解 (1)观察图象，得A ＝2，T ＝⎝ ⎛⎭⎪⎫11π12－π6×43＝π.∴ω＝2πT ＝2，∴f (x )＝2sin(2x ＋φ)． ∵函数经过点⎝ ⎛⎭⎪⎫π6，2，∴2sin ⎝ ⎛⎭⎪⎫2×π6＋φ＝2，即sin ⎝ ⎛⎭⎪⎫π3＋φ＝1.又∵|φ|<π2，∴φ＝π6，∴函数的解析式为f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6.(2)∵0<x <π，∴f (x )＝m 的根的情况，相当于f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6与g (x )＝m 的交点个数情况，且0<x <π，∴在同一坐标系中画出y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6和y ＝m (m ∈R )的图象．由图可知，当－2<m <1或1<m <2时，直线y ＝m 与曲线有两个不同的交点，即原方程有两个不同的实数根．∴m 的取值范围为－2<m <1或1<m <2；当－2<m <1时，此时两交点关于直线x ＝23π对称，两根和为43π；当1<m <2时，此时两交点关于直线x ＝π6对称，两根和为π3.高中数学-打印版精校版。

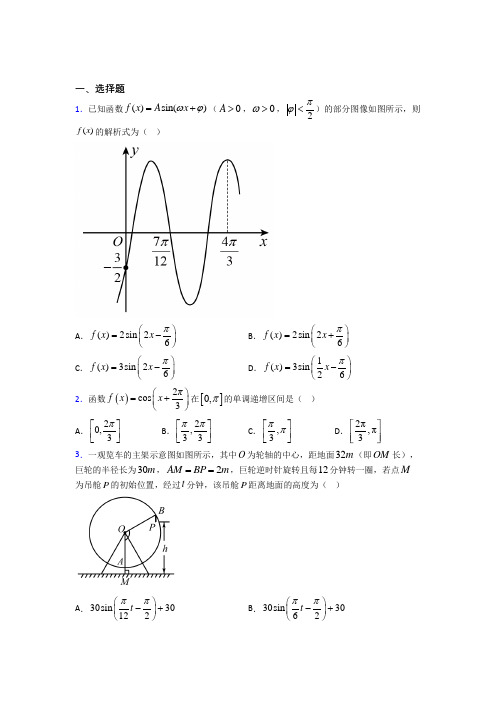
一、选择题1．已知函数()sin()f x A x ωϕ=+（0A >，0>ω，2πϕ<）的部分图像如图所示，则()f x 的解析式为（ ）A ．()2sin 26f x x π⎛⎫=- ⎪⎝⎭B ．()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C ．()3sin 26f x x π⎛⎫=-⎪⎝⎭D ．1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2．函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是（ ） A ．20,3π⎡⎤⎢⎥⎣⎦B ．2,33ππ⎡⎤⎢⎥⎣⎦C ．,3ππ⎡⎤⎢⎥⎣⎦D ．2π,π33．一观览车的主架示意图如图所示，其中O 为轮轴的中心，距地面32m （即OM 长），巨轮的半径长为30m ，2AM BP m ==，巨轮逆时针旋转且每12分钟转一圈，若点M 为吊舱P 的初始位置，经过t 分钟，该吊舱P 距离地面的高度为（ ）A ．30sin 30122t ππ⎛⎫-+⎪⎝⎭B ．30sin 3062t ππ⎛⎫-+⎪⎝⎭C ．30sin 3262t ππ⎛⎫-+⎪⎝⎭D ．30sin 62t ππ⎛⎫-⎪⎝⎭ 4．已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭，若方程()35f x =的解为1x ，2x （120x x π<<<），则()12sin x x -=（ ）A ．35B ．45-C ．D ．5．将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象，对于函数()y g x =有以下四个判断： ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭； ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称； ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增； ④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增. 其中，正确判断的序号是（ ） A ．②③B ．①②C ．②④D ．③④6．已知函数()()cos f x x ωϕ=+（0>ω，0πϕ-<<）的图象关于点,08π⎛⎫⎪⎝⎭对称，且其相邻对称轴间的距离为23π，将函数()f x 的图象向左平移3π个单位长度后，得到函数()g x 的图象，则下列说法中正确的是（ ）A ．()f x 的最小正周期23T π= B ．58πϕ=-C ．()317cos 248πx g x ⎛⎫=- ⎪⎝⎭D ．()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,82ππ⎡⎤⎢⎥⎣⎦7．筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中得到使用．假设在水流量稳定的情况下，简车上的每一个盛水筒都做逆时针匀速圆周运动．现将筒车抽象为一个几何图形，如图所示，圆O 的半径为4米，盛水筒M 从点0P 处开始运动，0OP 与水平面的所成角为30，且每分钟恰好转动1圈，则盛水筒M 距离水面的高度H （单位；m ）与时间t （单位：s ）之间的函数关系式的图象可能是（ ）A ．B ．C ．D ．8．下列结论正确的是（ ） A ．sin1cos1< B ．2317cos cos 54ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭C ．()()tan 52tan 47->-D ．sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭9．使函数()3)cos(2)f x x x θθ=+++是偶函数，且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是（ ） A ．6π B ．3π C ．23π D ．56π 10．已知函数()[][]sin cos cos sin f x x x =+，其中[]x 表示不超过实数x 的最大整数，则（ ）A ．()f x 是奇函数B ．π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C ．()f x 的一个周期是πD ．()f x 的最小值小于011．如图，摩天轮是一种大型转轮状的机械建筑设施，游客坐在摩天轮的座舱里慢慢地往上转，可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ，转盘直径为110m 设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要20min .游客甲坐上摩天轮的座舱，开始转动t min 后距离地面的高度为H m ，则在转动一周的过程中，高度H 关于时间t 的函数解析式是（ ）A ．()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B ．()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C ．()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D ．()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭12．已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性，且满足04g π⎛⎫= ⎪⎝⎭，()3g π=，则ω的取值共有（ ） A ．6个B ．5个C ．4个D ．3个二、填空题13．已知3()tan 1f x a x x =+（a ，b 为实数），且3(lg log 10)5f =，则(lglg3)f =____________．14．已知定义在R 上的函数()f x 满足：()()2f x f x π+=，且当[]0,x π∈时，()sin f x x =.若对任意的(],x m ∈-∞，都有()2f x ≤，则实数m 的取值范围是______. 15．如图，某公园要在一块圆心角为3π，半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ，若//EF AB ，则文化景观区域面积的最大值为______2m .16．若函数f (x )=2sin(ωx +φ)(ω>0，0<φ<π)的图象经过点,26π⎛⎫⎪⎝⎭，且相邻两条对称轴间的距离为2π，则4f π⎛⎫⎪⎝⎭的值为________. 17．设函数()y f x =的定义域为D ，若对任意的1x ∈D ，总存在2x ∈D ，使得()()121f x f x ⋅=，则称函数()f x 具有性质M ．下列结论：①函数3y x x =-具有性质M ； ②函数35x x y =+具有性质M ；③若函数()[]8log 2,0,y x x t =+∈具有性质M ，则510t =； ④若3sin y x a =+具有性质M ，则5a =． 其中正确结论的序号是____________．18．函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19．关于函数()4sin(2)(),3f x x x R π=+∈有下列命题：①由12()()0f x f x ==可得12x x -必是π的整数倍；②()y f x =的图象关于点(,0)6π-对称；③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.20．将函数()sin (0)f x x ωω=>的图象向右平移6π个单位长度，得到函数()y g x =的图像，若()y g x =是偶函数，则ω的最小值为________．三、解答题21．已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭，x ∈R .（1）用“五点法”画出函数()f x 一个周期内的图象； （2）求函数()f x 在[],ππ-内的值域； （3）若将函数()f x 的图象向右平移6π个单位长度，得到函数()g x 的图象，求函数()g x 在[],ππ-内的单调增区间.22．函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示：（1）求()f x 的解析式； （2）()f x 向左平移12π个单位后得到函数()g x ，求()g x 的单调递减区间；（3）若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥，求x 的取值范围．23．已知向量a ＝(cosωx －sinωx ，sinωx)，b ＝(－cosωx －sinωx,2cosωx)．设函数f(x)＝a b ⋅＋λ(x ∈R)的图象关于直线x ＝π对称，其中ω，λ为常数，且ω∈1,12⎛⎫⎪⎝⎭.(1)求函数f(x)的最小正周期； (2)若y ＝f(x)的图象经过点,04π⎛⎫⎪⎝⎭，求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围 24．已知函数()()()f x g x h x =，其()22g x x =，()h x =_____. （1）写出函数()f x 的一个周期（不用说明理由）； （2）当,44x ππ⎡⎤∈-⎢⎥⎣⎦时，求函数()f x 的最大值和最小值. 从①cos 4x π⎛⎫+⎪⎝⎭，②2sin 24x π⎛⎫- ⎪⎝⎭这两个条件中任选一个，补充在上面问题中并作答， 注：如果选择多个条件分别解答.按第一个解答计分. 25．已知sin(3)(),cos x f x x R xπ-=∈（1）若α为第三象限角，且3sin 5α=-，求()f α的值． （2）若,34x ππ⎡⎤∈-⎢⎥⎣⎦，且21()2()1cos g x f x x =++，求函数()g x 的最小值，并求出此时对应的x 的值．26．函数()cos()(0)f x x ωφω=+>的部分图像如图所示.（1）求()f x 的表达式； （2）若[1,2]x ∈，求()f x 的值域；（3）将()f x 的图像向右平移112个单位后，再将所得图像横坐标伸长到原来的2倍，纵坐标不变，得到函数()y g x =的图像，求()g x 的单调递减区间.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】 本题首先可根据33π44T 求出ω，然后根据当43x π=时函数()f x 取最大值求出ϕ，最后代入30,2⎛⎫- ⎪⎝⎭，即可求出A 的值. 【详解】因为4π7π3π3124，所以33π44T ，T π=，因为2T πω=，所以2ω=，()sin(2)f x A x ϕ=+，因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值，所以()42232k k Z ππϕπ⨯+=+∈，()26k k Z πϕπ=-+∈，因为2πϕ<，所以6πϕ=-，()sin 26f x A x π⎛⎫=- ⎪⎝⎭，代入30,2⎛⎫- ⎪⎝⎭，3sin 26A π⎛⎫-=- ⎪⎝⎭，解得3A =，()3sin 26f x x π⎛⎫=- ⎪⎝⎭， 故选：C. 【点睛】关键点点睛：本题考查根据函数图像求函数解析式，对于()sin()f x A x ωϕ=+，可通过周期求出ω，通过最值求出A ，通过代入点坐标求出ϕ，考查数形结合思想，是中档题.2．C解析：C 【分析】先求出函数的单调增区间，再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z )， 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z )， 当1k =-时，5233ππx -<<- 当0k =时，433x ππ<<又∵[]0,x π∈， 故选：C 【点睛】方法点睛：求三角函数()cos()f x A wx ϕ=+的单调区间，一般利用复合函数的单调性原理解答：首先是对复合函数进行分解，接着是根据复合函数的单调性原理分析出分解出的函数的单调性，最后根据分解函数的单调性求出复合函数的单调区间.3．B解析：B 【分析】先通过计算得出转动的角速度，然后利用三角函数模型表示在转动的过程中点B 的纵坐标满足的关系式，则吊舱到底面的距离为点B 的纵坐标减2. 【详解】如图所示，以点M 为坐标原点，以水平方向为x 轴，以OM 所在直线为y 轴建立平面直角坐标系.因为巨轮逆时针旋转且每12分钟转一圈，则转动的角速度为6π每分钟， 经过t 分钟之后，转过的角度为6BOA t π∠=，所以，在转动的过程中，点B 的纵坐标满足：3230sin 30sin 322662y t t ππππ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭则吊舱距离地面的距离30sin 32230sin 306262h t t ππππ⎛⎫⎛⎫=-+-=-+ ⎪ ⎪⎝⎭⎝⎭. 故选：B ． 【点睛】建立三角函数模型解决实际问题的一般步骤： （1）审题：审清楚题目条件、要求、理解数学关系； （2）建模：分析题目变化趋势，选择合适的三角函数模型； （3）求解：对所建立的数学模型进行分析研究，从而得到结论.4．B解析：B 【分析】求出函数()f x 在(0,)π上的对称轴，然后由正弦函数性质得1223x x π+=，这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭，而已知条件为23sin(2)65x π-=，再由正弦函数性质确定226x π-的范围，从而由平方关系求得结论．【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足：()262x k k Z πππ-=+∈，即()23k x k Z ππ=+∈，令0k =可得函数在区间()0,π上的一条对称轴为3x π=，结合三角函数的对称性可知1223x x π+=，则：1223x x π=-，()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，由题意：0πx <<，则112666x πππ-<-<，23sin 265x π⎛⎫-= ⎪⎝⎭，120x x π<<<，则2226x πππ<-<，由同角三角函数基本关系可知：24cos 265x π⎛⎫-=- ⎪⎝⎭， 故选：B ． 【点睛】关键点点睛：本题考查正弦函数的性质，考查平方关系．解题时根据自变量的范围求得此范围内函数的对称轴，从而得出两个变量12,x x 的关系，可化双变量为单变量，再根据函数值及函数性质确定出单变量的范围，从而求得结论．注意其中诱导公式的应用，目的是把求值式与已知条件中的角化为一致．5．A解析：A 【分析】根据函数平移变换得sin 2y x =，再根据正弦函数的性质依次讨论即可得答案. 【详解】解：由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知： 将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦，选项①错误； 令2x k =π，k Z ∈，求得2k x =π，k Z ∈， 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称， 令1k =，故函数的图象关于点,02π⎛⎫⎪⎝⎭对称，选项②正确； 则函数的单调递增区间满足：222()22k x k k Z ππππ-≤≤+∈，即()44k x k k Z ππππ-≤≤+∈，令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦，选项③正确，④错误.故选:A. 【点睛】本题考查三角函数平移变换，正弦型函数的单调区间，对称中心等，考查运算求解能力，解题的易错点在于平移变换时，当1ω≠时，须将ω提出，平移只针对x 进行平移，具体的在本题中，sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦，而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，是中档题. 6．D解析：D 【分析】首先根据三角函数的性质，可知相邻对称轴间的距离是半个周期，判断A ；再求函数的解析式，判断B ；根据平移规律得到函数()g x ，判断C ；最后根据函数()g x 的解析式，利用整体代入的方法求函数的单调递减区间. 【详解】相邻对称轴间的距离是半个周期，所以周期是43π，故A 不正确； 243T ππω==，解得：32ω=，()f x 的图象关于点,08π⎛⎫⎪⎝⎭对称，3,282k k Z ππϕπ∴⨯+=+∈，解得：5,16k k Z πϕπ=+∈ 0πϕ-<<, 1116πϕ∴=-，故B 不正确； ()311cos 216f x x π⎛⎫=- ⎪⎝⎭，向左平移3π个单位长度后得()31133cos cos 2316216g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 故C 不正确； 当02x π≤≤时，3339,2161616x πππ⎡⎤-∈-⎢⎥⎣⎦，当3390,21616x ππ⎡⎤-∈⎢⎥⎣⎦时，函数单调递减，即 ,82x ππ⎡⎤∈⎢⎥⎣⎦，故D 正确. 故选：D 【点睛】关键点点睛：本题的关键是根据三角函数的性质求得函数()f x 的解析式，第四个选项是关键，需根据整体代入的方法，先求33216x π-的范围，再确定函数的单调递减区间. 7．D解析：D 【分析】先根据题意建立坐标系，写出盛水筒M 距离水面的高度H 与时间t 之间的函数关系式，再根据关系式即可判断. 【详解】解：以O 为圆心，过点O 的水平直线为x 轴，建立如图所示的平面直角坐标系：0306xOP π∠==，OP ∴在()t s 内转过的角为：26030t t ππ=， ∴以x 轴正半轴为始边，以OP 为终边的角为：306t ππ-，P ∴点的纵坐标为：4sin 306t ππ⎛⎫-⎪⎝⎭， H ∴与t 之间的函数关系式为：4sin 2306H t ππ⎛⎫=-+⎪⎝⎭， 当sin 1306t ππ⎛⎫-= ⎪⎝⎭时，max 426H =+=， 当sin 1306t ππ⎛⎫-=-⎪⎝⎭时，max 422H =-+=-， 对A ，B ，由图像易知max min H H =-，故A ，B 错误； 对C ，max min H H <-，故C 错误； 对D ，max min H H >-，故D 正确. 故选：D. 【点睛】关键点点睛：本题解题的关键是理解题意，根据题意写出H 与t 之间的函数关系式.8．D解析：D 【分析】利用正弦函数的单调性可判断AD 选项的正误；利用正切函数的单调性可判断C 选项的正误；利用余弦函数的单调性可判断B 选项的正误. 【详解】对于A 选项，因为正弦函数sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增， 且01122ππ<-<<，则sin1sin 1cos12π⎛⎫>-=⎪⎝⎭，A 选项错误； 对于B 选项，因为余弦函数cos y x =在()0,π上为减函数，23233cos cos cos 555πππ⎛⎫-== ⎪⎝⎭，1717cos cos cos 444πππ⎛⎫-== ⎪⎝⎭， 3045πππ<<<，则3cos cos 54ππ<，即2317cos cos 54ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭，B 选项错误； 对于C 选项，当900x -<<时，正切函数tan y x =单调递增， 因为9052470-<-<-<，所以，()()tan 52tan 47-<-，C 选项错误；对于D 选项，因为正弦函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增，因为021018πππ-<-<-<，所以，sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭，D 选项正确. 故选：D. 【点睛】思路点睛：解答比较函数值大小问题，常见的思路有两个： （1）判断各个数值所在的区间； （2）利用函数的单调性直接解答.9．B解析：B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数，则(0)2sin()26f πθ=+=±，sin()1,662k πππθθπ+=±+=+，3k πθπ=+，当0k =时，3πθ=，()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =，当[0,]4x π∈时，2[0,]2x π∈，()2cos2f x x =为减函数，符合题意，所以选B.10．D解析：D 【分析】利用奇函数的性质判断A ，分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小，取特殊值验证的方法判断C ，分区间计算一个周期内的最小值，判断选项D 。

第一章单元质量评估时间：120分钟 满分：150分一、选择题(每小题5分，共60分)1．已知角α是第三象限角，则角－α的终边在( B ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限解析：∵角α是第三象限角，∴k ·360°＋180°<α<k ·360°＋270°，k ∈Z ，∴－k ·360°－270°<－α<－k ·360°－180°，k ∈Z .∴角－α的终边在第二象限．故选B.2．已知扇形AOB 的面积为4，圆心角的弧度数为2，则该扇形的弧长为( A )A ．4B ．2C ．1D ．8解析：S ＝12l ·r ＝12·α·r 2＝4，∵α＝2，∴r ＝2，∴l ＝α·r ＝4.3．点P 从点(－1,0)出发，沿单位圆x 2＋y 2＝1顺时针方向运动π3弧长到达Q 点，则Q 点的坐标为( A )A.⎝ ⎛⎭⎪⎫－12，32B.⎝ ⎛⎭⎪⎫－32，－12C.⎝ ⎛⎭⎪⎫－12，－32D.⎝⎛⎭⎪⎫－32，12解析：点P 从点(－1,0)出发，沿单位圆x 2＋y 2＝1顺时针方向运动π3弧长到达Q 点，如图，因此Q 点的坐标为⎝ ⎛⎭⎪⎫cos 2π3，sin 2π3，即⎝ ⎛⎭⎪⎫－12，32，故选A.4．若600°角的终边上有一点(－4，a )，则a 的值是( C )A ．－433 B ．4 3 C ．－4 3 D ．±4 3解析：∵tan600°＝tan(60°＋3×180°)＝tan60°＝3，又点(－4，a )在600°角的终边上，∴－a 4＝tan600°＝3，∴a ＝－4 3.5．sin1，cos1，tan1的大小关系为( C ) A ．sin1>cos1>tan1 B ．sin1>tan1>cos1 C ．tan1>sin1>cos1 D ．tan1>cos1>sin1解析：本题主要考查同角的不同三角函数值的大小．由于π4<1<π3，则有1>sin1>22>cos1，又tan1>1，故tan1>sin1>cos1，故选C.6．若函数y ＝sin(ωx ＋φ)(ω>0)的部分图象如图所示，则ω＝( B )A ．5B ．4C ．3D ．2解析：由图象可知函数的周期为π2，所以2πω＝π2，ω＝4. 7．已知tan θ＝2，则sin θsin 3θ－cos 3θ＝( C )A.13B.23C.107D.32解析：本题主要考查同角三角函数关系的应用.sin θsin 3θ－cos 3θ＝sin θ(sin 2θ＋cos 2θ)sin 3θ－cos 3θ＝tan 3θ＋tan θtan 3θ－1＝23＋223－1＝107，故选C.8．设a ＝sin33°，b ＝cos55°，c ＝tan35°，则( C ) A ．a >b >c B ．b >c >a C ．c >b >a D ．c >a >b解析：∵b ＝cos55°＝sin(90°－55°)＝sin35°，且35°>33°，根据y ＝sin x在(0°，90°)上单调递增，可得b >a ；结合三角函数线可知b <c ，∴c >b >a ，故选C.9．函数f (x )＝lgsin(π4－2x )的一个增区间为( C )A ．(3π8，7π8)B ．(7π8，9π8)C ．(5π8，7π8)D ．(－7π8，－3π8) 解析：本题主要考查三角函数的单调性的判断和单调区间的求法．由sin(π4－2x )>0，得sin(2x －π4)<0，∴π＋2k π<2x －π4<2π＋2k π(k ∈Z )．又f (x )＝lgsin(π4－2x )的增区间即为sin(π4－2x )在定义域内的增区间，即sin(2x －π4)在定义域内的减区间，故π＋2k π<2x －π4<3π2＋2k π(k ∈Z )，化简得5π8＋k π<x <7π8＋k π(k ∈Z )，当k ＝0时，5π8<x <7π8，故选C.10．已知函数y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x －π6，则以下说法正确的是( C )A ．函数的最小正周期为π4 B ．函数为偶函数C ．函数图象的一条对称轴为直线x ＝π3D ．函数在⎣⎢⎡⎦⎥⎤2π3，5π6上为减函数解析：该函数的最小正周期T ＝π2；因为f (－x )＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫－2x －π6＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x ＋π6，因此它是非奇非偶函数；函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π6在[2π3，5π6]上是减函数，但y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x －π6在[2π3，5π6]上是增函数，因此只有C 正确． 11．将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位长度后，得到一个偶函数的图象，则φ的一个可能取值为( B )A.3π4B.π4 C ．0 D ．－π4解析：将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位长度，得到函数y ＝sin[2(x ＋π8)＋φ]＝sin(2x ＋π4＋φ)的图象，因为此时函数为偶函数，所以π4＋φ＝π2＋k π，k ∈Z ，即φ＝π4＋k π，k ∈Z .令k ＝0，得φ＝π4，故选B.12．已知ω>0，函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π4在⎝ ⎛⎭⎪⎫π2，π上单调递减，则ω的取值范围是( A )A.⎣⎢⎡⎦⎥⎤12，54B.⎣⎢⎡⎦⎥⎤12，34C.⎝ ⎛⎦⎥⎤0，12 D ．(0,2] 解析：∵ω>0，x ∈⎝ ⎛⎭⎪⎫π2，π，∴π2ω＋π4<ωx ＋π4<πω＋π4，又y ＝sin x 的单调减区间是[2k π＋π2，2k π＋32π](k ∈Z )．∴⎩⎪⎨⎪⎧π2ω＋π4≥2k π＋π2，πω＋π4≤2k π＋32π，即4k ＋12≤ω≤2k ＋54(k ∈Z )．令k ＝0，得12≤ω≤54，故选A.(本题也可用排除法)二、填空题(每小题5分，共20分) 13.sin ⎝ ⎛⎭⎪⎫15π2＋αcos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫9π2－αcos ⎝ ⎛⎭⎪⎫3π2＋α＝－1.解析：原式＝sin ⎣⎢⎡⎦⎥⎤8π＋⎝ ⎛⎭⎪⎫α－π2cos (π2－α)sin ⎣⎢⎡⎦⎥⎤4π＋⎝ ⎛⎭⎪⎫π2－αcos ⎣⎢⎡⎦⎥⎤π＋⎝ ⎛⎭⎪⎫π2＋α＝sin ⎝ ⎛⎭⎪⎫α－π2sin αsin ⎝ ⎛⎭⎪⎫π2－α⎣⎢⎡⎦⎥⎤－cos ⎝ ⎛⎭⎪⎫π2＋α＝－cos αsin αcos α[]－()－sin α＝－1.14．函数y ＝2cos ⎝⎛⎭⎪⎫2x －π3的单调增区间是[k π＋23π，k π＋76π](k ∈Z )．解析：由题意得2k π＋π≤2x －π3≤2k π＋2π，k ∈Z .∴k π＋23π≤x ≤k π＋76π，k ∈Z .∴函数的单调递增区间为[k π＋23π，k π＋76π]，k ∈Z .15．已知tan α＝cos α，则sin α＝－1＋52. 解析：由于tan α＝sin αcos α＝cos α，则sin α＝cos 2α，所以sin α＝1－sin 2α，解得sin α＝－1＋52或sin α＝－1－52(舍去)． 16．已知函数f (x )＝3sin ⎝ ⎛⎭⎪⎫ωx －π6(ω>0)和g (x )＝2cos(2x ＋φ)＋1的图象的对称轴完全相同，若x ∈⎣⎢⎡⎦⎥⎤0，π2，则f (x )的取值范围是⎣⎢⎡⎦⎥⎤－32，3. 解析：∵f (x )与g (x )的图象的对称轴完全相同，∴f (x )与g (x )的最小正周期相等，∵ω>0，∴ω＝2，∴f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π6， ∵0≤x ≤π2，∴－π6≤2x －π6≤5π6，∴－12≤sin ⎝ ⎛⎭⎪⎫2x －π6≤1，∴－32≤3sin ⎝⎛⎭⎪⎫2x －π6≤3，即f (x )的取值范围是⎣⎢⎡⎦⎥⎤－32，3. 三、解答题(共70分)17．(本小题10分)已知tan α＝－34. (1)求2＋sin αcos α－cos 2α的值；(2)求sin (4π－α)cos (3π＋α)cos (π2＋α)cos (152π－α)cos (π－α)sin (3π－α)sin (－π－α)sin (132π＋α)的值． 解：(1)2＋sin αcos α－cos 2α＝2(sin 2α＋cos 2α)＋sin αcos α－cos 2αsin 2α＋cos 2α＝2sin 2α＋sin αcos α＋cos 2αsin 2α＋cos 2α＝2tan 2α＋tan α＋1tan 2α＋1＝2×(－34)2＋(－34)＋1(－34)2＋1＝98－34＋11＋916＝2225.(2)原式＝(－sin α)(－cos α)(－sin α)cos[7π＋(π2－α)](－cos α)sin αsin αsin[6π＋(π2＋α)]＝sin 2αcos αsin α－cos αsin 2αcos α＝－sin αcos α＝－tan α＝34.18．(本小题12分)已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，－π<φ<0)图象最低点的纵坐标是－3，相邻的两个对称中心是⎝ ⎛⎭⎪⎫π3，0和⎝ ⎛⎭⎪⎫5π6，0.(1)求f (x )的解析式； (2)求f (x )的值域； (3)求f (x )的图象的对称轴．解：(1)由题意知，A ＝3，T ＝2×⎝ ⎛⎭⎪⎫5π6－π3＝π，∴2πω＝π，∴ω＝2.∴f (x )＝3sin(2x ＋φ)．又点⎝ ⎛⎭⎪⎫π3，0在f (x )的图象上， ∴f ⎝ ⎛⎭⎪⎫π3＝0，∴3sin ⎝ ⎛⎭⎪⎫2π3＋φ＝0；∴sin ⎝ ⎛⎭⎪⎫2π3＋φ＝0，结合－π<φ<0，可得φ＝－2π3.∴f (x )＝3sin ⎝⎛⎭⎪⎫2x －2π3.(2)f (x )的值域是[－3，3]．(3)令2x －2π3＝π2＋k π(k ∈Z )，得x ＝7π12＋k π2(k ∈Z )．∴f (x )的图象的对称轴是x ＝7π12＋k π2(k ∈Z )．19．(本小题12分)已知函数f (x )＝2a sin ⎝ ⎛⎭⎪⎫x －π4＋a ＋b .(1)当a ＝1时，求函数f (x )的单调递减区间；(2)当a <0时，f (x )在[0，π]上的值域为[2,3]，求a ，b 的值．解：(1)当a ＝1时，f (x )＝2sin ⎝ ⎛⎭⎪⎫x －π4＋1＋b .令2k π＋π2≤x －π4≤2k π＋3π2(k ∈Z )．解得2k π＋3π4≤x ≤2k π＋7π4(k ∈Z )．∴f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤2k π＋3π4，2k π＋7π4(k ∈Z )． (2)f (x )＝2a sin ⎝ ⎛⎭⎪⎫x －π4＋a ＋b ，∵x ∈[0，π]，∴－π4≤x －π4≤3π4，∴－22≤sin ⎝ ⎛⎭⎪⎫x －π4≤1.又∵a <0，∴2a ≤2a sin ⎝ ⎛⎭⎪⎫x －π4≤－a ，∴2a ＋a ＋b ≤f (x )≤b .∵f (x )的值域是[2,3]，∴2a ＋a ＋b ＝2且b ＝3.解得a ＝1－2，b ＝3.20．(本小题12分)如图，设A 是单位圆和x 轴正半轴的交点，P ，Q 是单位圆上的两点，O 是坐标原点，且∠AOP ＝β，β∈(0，π2)，∠AOQ ＝α，α∈[0，π)．(1)若点Q 的坐标是(m ，45)，其中m <0，求cos(π－α)＋sin(－α)的值； (2)设点P (32，12)，函数f (α)＝sin(α＋β)，求f (α)的值域．解：(1)由⎩⎨⎧m 2＋(45)2＝1，m <0得m ＝－35，所以cos α＝m ＝－35，sin α＝45.所以cos(π－α)＋sin(－α)＝－cos α－sin α＝－15.(2)由已知得β＝π6，因为α∈[0，π)，则α＋π6∈[π6，7π6)，所以－12<sin(α＋π6)≤1.故f (α)的值域是(－12，1]．21.(本小题12分) 设x ∈R ，函数f (x )＝cos(ωx ＋φ)(ω>0，－π2<φ<0)的最小正周期为π，且f (π4)＝32.(1)求ω和φ的值；(2)在给定坐标系中作出函数f (x )在[0，π]上的图象； (3)若f (x )>22，求x 的取值范围．解：(1)∵函数f (x )的最小正周期T ＝2πω＝π，∴ω＝2.∵f (π4)＝cos(2×π4＋φ)＝cos(π2＋φ)＝－sin φ＝32，且－π2<φ<0，∴φ＝－π3.(2)由(1)知f (x )＝cos(2x －π3)，列表如下：x 0 π6 5π12 2π3 11π12 π 2x －π3 －π3 0 π2 π 3π2 5π3 f (x )121－112作图象如图所示：(3)∵f (x )>22，即cos(2x －π3)>22，∴2k π－π4<2x －π3<2k π＋π4(k ∈Z )，则2k π＋π12<2x <2k π＋7π12(k ∈Z )，即k π＋π24<x <k π＋7π24(k ∈Z )．∴x 的取值范围是{x |k π＋π24<x <k π＋7π24，k ∈Z }．22．(本小题12分)已知函数f (x )＝A sin(ωx ＋φ)＋b (A >0，ω>0，|φ|<π2)的一系列对应值如下表：x －π6 π3 5π6 4π3 11π6 7π3 17π6 10π3 f (x )－1131－1131(1)根据表格提供的数据求函数f (x )的解析式；(2)根据(1)的结果，若函数y ＝f (kx )(k >0)的最小正周期为2π3，当x ∈[0，π3]时，方程f (kx )＝m 恰有两个不同的实数解，求实数m 的取值范围．解：(1)设f (x )的最小正周期为T ，由表格中的数据，得T ＝11π6－(－π6)＝2π，由T ＝2πω＝2π，得ω＝1.又⎩⎪⎨⎪⎧ b ＋A ＝3，b －A ＝－1，解得⎩⎪⎨⎪⎧A ＝2，b ＝1，令ω·5π6＋φ＝2k π＋π2(k ∈Z )，即5π6＋φ＝2k π＋π2(k ∈Z )，解得φ＝2k π－π3(k ∈Z )，又|φ|<π2，所以φ＝－π3.所以f (x )＝2sin(x －π3)＋1.(2)因为函数y ＝f (kx )＝2sin(kx －π3)＋1的最小正周期为2π3，所以k ＝2π2π3＝3，令t ＝3x －π3，因为x ∈[0，π3]，所以t ∈[－π3，2π3]，作出y ＝sin t (t ∈[－π3，2π3])的图象，如图所示．由图象可知，sin t ＝s 在t ∈[－π3，2π3]上有两个不同的实数解时，s ∈[32，1)，所以方程f (kx )＝m 在x ∈[0，π3]上恰好有两个不同实数解时，m ∈[3＋1,3)，即实数m 的取值范围是[3＋1,3)．。

单元评估验收(一)(时间：120分钟 满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．给出下列四种说法，其中正确的是( )①－75°是第四象限角 ②225°是第三象限角 ③475°是第二象限角 ④－315°是第一象限角A ．1个B ．2个C ．3个D ．4个答案：D2．已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为( ) A ．2B.2sin 1C ．sin 2D ．2sin 1解析：因为r ＝1sin 1，所以l ＝αr ＝2sin 1.答案：B3．设α是第三象限角，且⎪⎪⎪⎪⎪⎪cos α2＝－cos α2，则α2的终边所在的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：因为α是第三象限角，所以π＋2k π<α<3π2＋2k π，k ∈Z ，所以π2＋k π<α2<3π4＋k π，k ∈Z ，所以α2的终边在第二象限或第四象限． 又⎪⎪⎪⎪⎪⎪cos α2＝－cos α2，所以cos α2<0，所以α2的终边所在的象限是第二象限． 答案：B4．把函数f (x )＝sin 2x ＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数g (x )的图象，则g (x )的最小正周期为( )A ．2πB ．πC.π2D.π4解析：由题意知g (x )＝sin ⎝ ⎛⎭⎪⎫2×12x ＋1＝sin x ＋1，故T ＝2π. 答案：A5．设α是第二象限角，P (x ，4)为其终边上的一点，且cos α＝15x ，则tan α＝( )A.43B.34C ．－34D ．－43解析：α是第二象限角，所以x <0，r ＝x 2＋16， 所以cos α＝xx 2＋16＝15x ，所以x 2＝9，所以x ＝－3， 所以tan α＝－43.答案：D6．设g (x )的图象是由函数f (x )＝cos 2x 的图象向左平移π3个单位得到的，则g ⎝ ⎛⎭⎪⎫π6等于( )A ．1B ．－12C ．0D ．－1解析：由f (x )＝cos 2x 的图象向左平移π3个单位得到的是g (x )＝cos ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x ＋π3的图象，则g ⎝ ⎛⎭⎪⎫π6＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π6＋π3＝cos π＝－1.答案：D7．如果sin α－2cos α3sin α＋5cos α＝－5，那么tan α的值为( )A ．－2B ．2C.2316D ．－2316解析：因为sin α－2cos α＝－5(3sin α＋5cos α)， 所以16sin α＝－23cos α，所以tan α＝－2316.答案：D8．已知a 是实数，则函数f (x )＝1＋a sin ax 的图象不可能是( )解析：对于D 选项，由图知，振幅|a |>1⇒周期T ＝2π|a |应小于2π，与图中T >2π矛盾．答案：D9．若sin α是5x 2－7x －6＝0的根，则sin ⎝ ⎛⎭⎪⎫－α－3π2sin ⎝ ⎛⎭⎪⎫3π2－αtan 2（2π－α）cos ⎝ ⎛⎭⎪⎫π2－αcos ⎝ ⎛⎭⎪⎫π2＋αsin （π＋α）＝( )A.35B.53C.45D.54解析：方程5x 2－7x －6＝0的两根为x 1＝－35，x 2＝2.则sin α＝－35，原式＝cos α（－cos α）tan 2αsin α（－sin α）（－sin α）＝－1sin α＝53.答案：B10．函数y ＝11－x 的图象与函数y ＝sin πx (－2≤x ≤4)的图象所有交点的横坐标之和等于( )A ．2B ．4C ．6D ．8解析：如图，两个函数的图象都关于点(1，0)成中心对称，两个图象在[－2，4]上共有8个交点，每两个对应交点横坐标之和为2，故所有交点的横坐标之和为8.答案：D11．已知函数f (x )＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x －π6，则下列说法中正确的是( ) A ．函数f (x )的周期是π4B ．函数f (x )的图象的一条对称轴方程是x ＝π3C ．函数f (x )在区间⎣⎢⎡⎦⎥⎤2π3，5π6上为减函数D ．函数f (x )是偶函数解析：当x ＝π3时，f (x )＝1，所以x ＝π3是函数图象的一条对称轴．答案：B12．已知某帆船中心比赛场馆区的海面上每天海浪高度y (米)可看作是时间t (0≤t ≤24，单位：时)的函数，记作y ＝f (t )，经长期观测，y ＝f (t )的曲线可近似地看成是函数y ＝A cosωt ＋b ，下表是某日各时的浪高数据：A ．y ＝12cos π6t ＋1B ．y ＝12cos π6t ＋32C ．y ＝2cos π6t ＋32D ．y ＝12cos6πt ＋32解析：因为T ＝12－0＝12，所以ω＝2πT ＝2π12＝π6.又最大值为2，最小值为1， 则⎩⎪⎨⎪⎧A ＋b ＝2，－A ＋b ＝1，解得A ＝12，b ＝32，所以y ＝12cos π6t ＋32.答案：B二、填空题(本大题共4个小题，每小题5分，共20分．把答案填在题中的横线上) 13．已知点P (tan α，cos α)在第三象限，则角α的终边在第________象限． 解析：因为点P (tan α，cos α)在第三象限， 所以tan α<0，cos α<0，则α是第二象限角． 答案：二14．设a 为常数，且a >1，0≤x ≤2π，则函数f (x )＝cos 2x ＋2a sin x －1的最大值为________．解析：f (x )＝cos 2x ＋2a sin x －1＝1－sin 2x ＋2a sin x －1＝－(sin x －a )2＋a 2， 因为0≤x ≤2π，所以－1≤sin x ≤1，又a >1，所以当sin x ＝1时，f (x )max ＝－(1－a )2＋a 2＝2a －1. 答案：2a －115．函数f (x )＝sin(ωx ＋φ)(ω>0，φ∈[0，2π))的部分图象如图所示，则f (2 018)＝________．解析：由题图可知，T 4＝2，所以T ＝8，所以ω＝π4.由点(1，1)在函数图象上，可得f (1)＝sin ⎝ ⎛⎭⎪⎫π4＋φ＝1，故π4＋φ＝2k π＋π2(k ∈Z)，所以φ＝2k π＋π4(k ∈Z)，又φ∈[0，2π)，所以φ＝π4.故f (x )＝sin ⎝ ⎛⎭⎪⎫π4x ＋π4，所以f (2 018)＝sin ⎝ ⎛⎭⎪⎫2 018π4＋π4＝sin ⎝ ⎛⎭⎪⎫504π＋34π＝sin 34π＝22.答案：2216．已知f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π6－m 在x ∈⎣⎢⎡⎦⎥⎤0，π2上有两个不同的零点，则m 的取值范围是________________．解析：f (x )有两个零点，即m ＝2sin ⎝ ⎛⎭⎪⎫2x －π6，在⎣⎢⎡⎦⎥⎤0，π2上有两个不同的实根．当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π6∈⎣⎢⎡⎦⎥⎤－π6，56π，结合正弦曲线知m ∈[1，2)． 答案：[1，2)三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)(1)已知角α的终边经过点P (4，－3)，求2sin α＋cos α的值；(2)已知角α的终边经过点P (4a ，－3a )(a ≠0)，求2sin α＋cos α的值；(3)已知角α终边上一点P 与x 轴的距离和与y 轴的距离之比为3∶4，求2sin α＋cosα的值．解：(1)因为r ＝x 2＋y 2＝5，所以sin α＝y r ＝－35，cos α＝x r ＝45，所以2sin α＋cos α＝－65＋45＝－25.(2)因为r ＝x 2＋y 2＝5|a |，所以当a >0时，r ＝5a ，所以sin α＝－3a 5a ＝－35，cos α＝45，所以2sin α＋cos α＝－25；当a <0时，r ＝－5a ，所以sin α＝－3a －5a ＝35，cos α＝－45，所以2sin α＋cos α＝25.(3)当点P 在第一象限时，sin α＝35，cos α＝45，2sin α＋cos α＝2；当点P 在第二象限时，sin α＝35，cos α＝－45，2sin α＋cos α＝25；当点P 在第三象限时，sin α＝－35，cos α＝－45，2sin α＋cos α＝－2；当点P 在第四象限时，sin α＝－35，cos α＝45，2sin α＋cos α＝－25. 18．(本小题满分12分)已知函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π6＋a ，a 为常数．(1)求函数f (x )的最小正周期；(2)若x ∈⎣⎢⎡⎦⎥⎤0，π2时，f (x )的最小值为－2，求a 的值．解：(1)f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π6＋a .所以f (x )的最小正周期T ＝2π2＝π. (2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，所以x ＝0时，f (x )取得最小值，即2sin ⎝ ⎛⎭⎪⎫－π6＋a ＝－2，故a ＝－1.19．(本小题满分12分)某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，||φ<π2在某一个周期内的图象时，列表并填入了部分数据，如下表：(1)(2)将y ＝f (x )图象上所有点向左平行移动π6个单位长度，得到y ＝g (x )的图象，求y ＝g (x )的图象离原点O 最近的对称中心．解：(1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6.数据补全如下表：且函数表达式为f (x )＝5sin ⎝ ⎛⎭⎪⎫2x －6. (2)由(1)知f (x )＝5sin ⎝⎛⎭⎪⎫2x －π6， 因此g (x )＝5sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π6－π6＝5sin ⎝ ⎛⎭⎪⎫2x ＋π6. 因为y ＝sin x 的对称中心为(k π，0)，k ∈Z ， 令2x ＋π6＝k π，k ∈Z ，解得x ＝k π2－π12，k ∈Z ，即y ＝g (x )图象的对称中心为⎝⎛⎭⎪⎫k π2－π12，0，k ∈Z ，其中离原点O 最近的对称中心为⎝ ⎛⎭⎪⎫－π12，0. 20．(本小题满分12分)已知f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋32，x ∈R.(1)求函数f (x )的最小正周期和单调递增区间．(2)函数f (x )的图象可以由函数y ＝sin 2x (x ∈R)的图象经过怎样的变换得到？ 解：(1)T ＝2π2＝π，2k π－π2≤2x ＋π6≤2k π＋π2，k ∈Z ，知k π－π3≤x ≤k π＋π6(k∈Z)．所以函数f (x )的最小正周期为π，单调递增区间为⎣⎢⎡⎦⎥⎤k π－π3，k π＋π6(k ∈Z)．(2)变换情况如下：y ＝sin 2xy ＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π12――――――――→将图象上各点向上平移32个单位长度y ＝sin(2x ＋π6)＋32.21．(本小题满分12分)已知函数y ＝A sin(ωx ＋φ)(A >0，ω>0，|ω|<π)的一段图象如图所示．(1)求此函数的解析式；(2)求此函数在(－2π，2π)上的递增区间． 解：(1)由图可知，其振幅为A ＝23， 由于T2＝6－(－2)＝8，所以周期为T ＝16， 所以ω＝2πT ＝2π16＝π8，此时解析式为y ＝23sin ⎝ ⎛⎭⎪⎫π8x ＋φ.因为点(2，－23)在函数y ＝23sin ⎝ ⎛⎭⎪⎫π8x ＋φ的图象上，所以π8×2＋φ＝2k π－π2，所以φ＝2k π－3π4(k ∈Z)．又|φ|<π，所以φ＝－3π4.故所求函数的解析式为y ＝23sin ⎝ ⎛⎭⎪⎫π8x －3π4.(2)由2k π－π2≤π8x －3π4≤2k π＋π2(k ∈Z)，得16k ＋2≤x ≤16k ＋10(k ∈Z)，所以函数y ＝23sin ⎝ ⎛⎭⎪⎫π8x －3π4的递增区间是[16k ＋2，16k ＋10](k ∈Z)．当k ＝－1时，有递增区间[－14，－6]，当k ＝0时，有递增区间[2，10]，与定义区间求交集得此函数在(－2π，2π)上的递增区间为(－2π，－6]和[2，2π]． 22．(本小题满分12分)已知函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π3.(1)求函数f (x )的最小值及f (x )取到最小值时自变量x 的集合；(2)指出函数y ＝f (x )的图象可以由函数y ＝sin x 的图象经过哪些变换得到； (3)当x ∈[0，m ]时，函数y ＝f (x )的值域为[－3，2]，求实数m 的取值范围． 解：(1)f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π3，故f (x )min ＝－2，此时2x －π3＝2k π－π2，k ∈Z ，即x ＝k π－π12，k ∈Z ，即此时自变量x 的集合是⎩⎨⎧⎭⎬⎫x |x ＝k π－π12，k ∈Z .(2)把函数y ＝sin x 的图象向右平移π3个单位长度，得到函数y ＝sin ⎝ ⎛⎭⎪⎫x －π3的图象，再把函数y ＝sin ⎝ ⎛⎭⎪⎫x －π3的图象上所有点的纵坐标不变，横坐标变为原来的12，得到函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的图象，最后再把函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的图象上所有点的横坐标不变，纵坐标变为原来的2倍，得到函数y ＝2sin ⎝⎛⎭⎪⎫2x －π3的图象．(3)如图，因为当x ∈[0，m ]时，y ＝f (x )取到最大值2，且f (0)＝－3， 所以2m －π3≥π2⇒m ≥5π12.又函数y ＝f (x )在⎣⎢⎡⎦⎥⎤5π12，11π12上是单调减函数，故m 的最大值为在⎣⎢⎡⎦⎥⎤5π12，11π12内使函数值为－3的x 的值，令2sin ⎝ ⎛⎭⎪⎫2x －π3＝－3，得x ＝5π6， 所以m 的取值范围是⎣⎢⎡⎦⎥⎤5π12，5π6.。

单元素养评价（一）（第一章)(120分钟150分)一、选择题(每小题5分,共60分）1。

若=2kπ+(k∈Z)，则的终边在（）A。

第一象限 B.第四象限C。

x轴上D。

y轴上【解析】选D。

由=2kπ+，k∈Z,可得α=6kπ+π,k∈Z，所以=3kπ+，k∈Z,当k为奇数时,的终边在y轴的非正半轴上，当k为偶数时,的终边在y轴的非负半轴上，综上可知，终边在y轴上。

2。

若一个α角的终边上有一点P（—4，a）,且sin α·cos α=,则a的值为（）A。

4 B.±4C。

—4或-D。

【解析】选C。

由三角函数定义可知，r=，sin α=，cos α=,sin α·cos α==，解得a=—4或—.3.（2020·宜昌高一检测）已知扇形AOB的周长为4，当扇形的面积取得最大值时，扇形的弦长AB等于( ) A.2 B。

sin 1 C。

2sin 1 D。

2cos 1【解析】选C。

设扇形的半径为r，可得出扇形的弧长为l=4—2r(0<r〈2)，所以，扇形的面积为S=lr=r(4—2r)=—r2+2r=—（r—1）2+1，当r=1时，该扇形的面积取到最大值1，扇形的弧长为l=4—2r=2，此时∠AOB==2，如图所示。

取AB的中点C,则OC⊥AB,且∠AOC=1，因此，AB=2AC=2rsin 1=2sin 1。

4。

点P从(1,0）点出发,沿单位圆x2+y2=1逆时针方向运动弧长到达Q点，则Q点坐标为 ( ）A。

B。

C。

D。

【解析】选A.设∠POQ=θ,则θ=.又设Q(x,y），则x=cos=，y=sin=。

5。

(2020·天津高考）已知函数f（x）=sin。

给出下列结论：①f（x）的最小正周期为2π;②f是f（x)的最大值；③把函数y=sin x的图象上所有点向左平移个单位长度，可得到函数y=f(x）的图象.其中所有正确结论的序号是（）A.① B.①③ C。

高中数学学习材料马鸣风萧萧*整理制作单元质量评估（一）第一章：三角函数一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.把-495°表示成k×360°+θ(k∈Z)的形式，则θ可以是（）(A)-135° (B)45° (C)-225° (D)135°【解析】选A.由题意可知-495°=k×360°+θ,从而θ=-495°-k×360°.当k=-1时,θ=-135°.2.若2弧度的圆心角所对的弧长为2 cm,则这个圆心角所夹的扇形的面积是（）(A)4 cm2 (B)2 cm2(C)4π cm2 (D)1 cm2【解析】选D.由弧长公式得2=2R,即R=1 cm,则S=R l=×1×2=1 (cm2).3.（2009·济南高一检测）化简sin600°的值是（）【解析】选D.sin600°=sin240°=sin(180°+60°)=-sin60°=.4.（2009·上海高一检测）已知a∈R，函数f(x)=sinx-|a|,x∈R为奇函数，则a=（）（A）0 （B）1 （C）-1 （D）±1【解析】选A.∵f(x)是奇函数，x∈R,∴f(0)=0,即-|a|=0,∴a=0.5.已知角θ的终边过点(4,-3),则cos(π-θ)等于（）6.（tanx+）cos2x等于( )(A)tanx (B)sinx (C)cosx (D)7.下列四个函数中，周期为π的是( )（A） y=sinx （B）y=2cosx（C）y=sin（D）y=|cosx|【解析】选D.对A、B，周期均为2π,对C，T==4π,对D,结合y=|cosx|的图象知，其周期为π.8.（2009·辽宁高考）已知tanθ=2,则sin2θ+sinθcosθ-2cos2θ=( )9.已知函数f(x)=3sin(),则下列不等式中正确的是（）(A)f(1)<f(2)<f(3)(B)f(2)<f(3)<f(1)(C)f(3)<f(2)<f(1)(D)f(2)<f(1)<f(3)12.（2009·烟台模拟）车流量被定义为单位时间内通过十字路口的车辆数，单位为辆/分，上班高峰期某十字路口的车流量由函数F（t）=50+4sin (其中0≤t≤20)给出，F（t）的单位是辆/分，t的单位是分，则下列哪个时间段内车流量是增加的( )(A)［0,5］ (B)［5,10］(C)［10,15］ (D)［15,20］【解析】选C.由得4kπ-π≤t≤4kπ+π(k∈Z),由于0≤t≤20,∴0≤t≤π或3π≤t≤5π,从而车流量在时间段［10,15］内是增加的.二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上）13.函数y=tan(2x- )的定义域为_______.14.（2009·辽宁高考）已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示，则ω=______.15.（2009·上海模拟）已知x= 是方程3tan(x+α)= 的一个解,α∈（-π,0），则α=______.16.（2009·盐城高一检测）把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半，纵坐标不变，再把图象向左平移个单位，这时对应的图象的解析式为_______.21.（12分）已知函数f(x)=Asin(ωx+φ)+m(A>0,ω>0,|φ|< )的最大值是4,最小值是0,最小正周期是,直线x= 是函数图象的一条对称轴,求其解析式.22.（12分）已知，如图表示电流强度I与时间t的关系I=Asin(ωt+φ)在一个周期内的图象.(1)试根据图象写出I=Asin(ωt+φ)的解析式；(2)为了使I=Asin(ωt+φ)中t在任意一段秒的时间内电流强度I能同时取得最大值|A|与最小值-|A|，那么，正整数ω的最小值是多少？。