正弦函数余弦函数的图象学案(人教A版必修4)

1.4.2正弦函数、余弦函数的性质（二）［学习目标］1•掌握y=sin x, y=cos x的最大值与最小值，并会求简单三角函数的值域和最值2掌握j；=sinx, j/=cosx的单调性，并能利用单调性比较大小.3.会求函数y=Asin（^x+（p）及y=A cos（ex+卩）的单调区间.戸预习导学全挑战自我，点点落实______________________________________________________________［知识链接］1.怎样求函数fix）=Asin（cox+（/））（或./（x）=/cos（亦+卩））的最小正周期答由诱导公式一知：对任意xGR,都有Asin［（a）x+（p） + 2TI］=Asin（cox+（p）,所以./W=A sin（cox+（p）（co0）是周期函数，方就是它的一个周期.由于兀至少要增加两个单位，/（X）的函数值才会重复出现，因此，两是函数/（x）=/sin（ex+°）的最小正周期.同理，函数/（x）=/cos（砂+卩）也是周期函数，最小正周期也是壽.2.观察正弦曲线和余弦曲线，正弦、余弦函数是否存在最大值和最小值？若存在，其最大值和最小值分别为多少？答正弦、余弦函数存在最大值和最小值，分别是1和一1.［预习导引］正弦函数、余弦函数的性质函数y=sinx y=cosx图象-i-TT \J/定义域R R值域[-1,11[-1,11对称性对称轴：兀=航+畝WZ）；对称中心：伙兀，0）伙EZ）对称轴：x=k7t（k^Z）；对称中心：仏+号’0）所以Asin=Asin（cox+（p）,(©)奇偶性 奇函数 偶函数 周期性最小正周期：2兀最小正周期：2K单调性JTTT在［一㊁+2ht,㊁+2加］伙GZ ）上单调递增;在奇+2fac,夢+在［—TT +2E, 2E ］伙WZ ）上单调递增；在［2/CTT , n + 2/m ］ 伙WZ ）上单调递减最值71 当 X —2 + 2加伙GZ)时，Jniax =1；当x=—号+2加伙丘Z)时'J^min — — 1当x=2刼伙WZ)时，亦=1；当 X = 7t + 2kjt(k^Z)时，加n =-1歹课堂讲义 /重点难点，个个击破 _____________________________________________________________要点一 求正弦、余弦函数的单调区间兀 则y =—2si n z .因为z 是x 的一次函数，所以要求y=-2sinz 的递增区间, 即求sinz 的递减区间， 即2航+号壬冬2加+守伙丘2）. TT兀 3TT•: 2A TT +，W X —玄冬2航十㊁伙G Z ）,3兀 7兀 2£兀+才WxW2加十才伙G Z ）,求函数y=2sin卜x)的单调递增区间. 例1 的递增区间为2&兀+乎,2£兀+晋伙UZ).规律方法用整体替换法求函数y=Asin（cox+（p）或y=Acos（ojx+（p）的单调区间时，如果式子中X的系数为负数，先利用诱导公式将兀的系数变为正数再求其单调区间.再将最终结果写成区间形式.跟踪演练1求下列函数的单调递增区间:(l”=l+2sin(£-"；(2)尹=lo#cos x.令u=x-^则根据复合函数的单调性知，所给函数的单调递增区间就是^=sin U 的单调递 减区间，即2加+㊁尹仇GZ),ITJr3兀亦即2刼+㊁Wx —&W2A TT +亍伙WZ).2 S 亦即2£兀+尹冬兀冬2加+尹伙丘乙)，故函数y=l+2sin(?—x)的单调递增区间是2加+|兀，2刼+刍:伙WZ). 兀 兀 (2)由 cosx>0,得 2«兀一㊁<x<2hr+㊁，k^Z.・・・*< 1，・・・函数尸log|cos X 的单调递增区间即为 w = cosx, x^\2kit —y 2航+办圧Z)的递减区间,故函数J*=log|cosx 的单调递增区间为2H, 2加+引伙GZ).要点二正弦、余弦函数的单调性的应用例2利用三角函数的单调性，比较下列各组数的大小.(2)sin 196。

1．4.1 正弦函数、余弦函数的图象1．4.2 正弦函数、余弦函数的性质考试标准知识导图学法指导1.本节内容以三角函数的图象及其性质为主，因此在学习过程中应先学会作图，然后利用图象研究函数的性质．2．深刻理解五点的取法，特别是非正常周期的五点．3．注意所有的变换是图象上的点在移动，是x 或y 在变化而非ωx .4．运用整体代换的思想，令ωx ＋φ＝t ，借助y ＝sin t ，y ＝cos t 的图象和性质研究函数y ＝sin(ωx ＋φ)，y ＝cos(ωx ＋φ)的图象和性质．第1课时 正弦函数、余弦函数的图象正弦曲线与余弦曲线及其画法状元随笔 1.关于正弦函数y ＝sin x 的图象(1)正弦函数y ＝sin x ，x∈[2k π，2(k ＋1)π]，k∈Z 的图象与x ∈[0,2π]上的图形一致，因为终边相同角的同名三角函数值相等．(2)正弦函数的图象向左、右无限延伸，可以由y ＝sin x ，x ∈[0,2π]图象向左右平移得到(每次平移2π个单位)．2．“几何法”和“五点法”画正、余弦函数的比较(1)“几何法”就是利用单位圆中正弦线和余弦线作出正、余弦函数图象的方法. 该方法作图较精确，但较为烦琐．(2)“五点法”是画三角函数图象的基本方法，在要求精度不高的情况下常用此法． 提醒：作图象时，函数自变量要用弧度制，自变量与函数值均为实数，因此在x 轴、y 轴上可以统一单位，这样作出的图象正规便于应用．[小试身手]1．判断下列命题是否正确. (正确的打“√”，错误的打“×”)(1)“五点法”作正、余弦函数的图象时的“五点”是指图象上的任意五点．( )(2)正弦函数在⎣⎢⎡⎦⎥⎤－3π2，π2和⎣⎢⎡⎦⎥⎤π2，5π2上的图象相同．( )(3)正弦函数、余弦函数的图象分别向左、右无限延伸．( ) 答案：(1)× (2)√ (3)√2．以下对正弦函数y ＝sin x 的图象描述不正确的是( )A ．在x ∈[2k π，2(k ＋1)π](k ∈Z )上的图象形状相同，只是位置不同B ．介于直线y ＝1与直线y ＝－1之间C ．关于x 轴对称D ．与y 轴仅有一个交点解析：画出y ＝sin x 的图象，根据图象可知A ，B ，D 三项都正确． 答案：C3．下列图象中，是y ＝－sin x 在[0,2π]上的图象的是( )解析：函数y ＝－sin x 的图象与函数y ＝sin x 的图象关于x 轴对称，故选D. 答案：D4．用“五点法”作函数y ＝cos 2x ，x ∈R 的图象时，首先应描出的五个点的横坐标是________________．解析：令2x ＝0，π2，π，3π2和2π，得x ＝0，π4，π2，34π，π.答案：0，π4，π2，34π，π类型一 用“五点法”作三角函数的图象例1 用“五点法”作出下列函数的简图： (1)y ＝sin x ＋12，x ∈[0,2π]；(2)y ＝1－cos x ，x ∈[0,2π]． 【解析】 (1)按五个关键点列表：(2)列表：作函数图象需要先列表再描点，最后用平滑曲线连线． 方法归纳作形如y ＝a sin x ＋b (或y ＝a cos x ＋b )，x ∈[0,2π]的图象的三个步骤跟踪训练1 画出函数y ＝3＋2cos x 的简图． 解析：(1)列表，如下表所示(2)利用五点作图法画简图．类型二 正、余弦函数曲线的简单应用 例2 根据正弦曲线求满足sin x ≥－32在[0,2π]上的x 的取值范围． 【解析】 在同一坐标系内作出函数y ＝sin x 与y ＝－32的图象，如图所示．观察在一个闭区间[0,2π]内的情形，满足sin x ≥－32的x ∈⎣⎢⎡⎦⎥⎤0，43π∪⎣⎢⎡⎦⎥⎤53π，2π，所以满足sin x ≥－32在[0,2π]上的x 的范围是{x 0≤x ≤43π或5π3≤x ≤2π}.或⎣⎢⎡⎦⎥⎤0，43π∪⎣⎢⎡⎦⎥⎤53π，2π在同一坐标系内作y ＝sin x 与y ＝－32的图象，利用图象求x 的范围. 方法归纳利用三角函数图象解sin x >a (或cos x >a )的三个步骤 (1)作出直线y ＝a ，y ＝sin x (或y ＝cos x )的图象． (2)确定sin x ＝a (或cos x ＝a )的x 值． (3)确定sin x >a (或cos x >a )的解集．[注意] 解三角不等式sin x >a ，如果不限定范围时，一般先利用图象求出x ∈[0,2π]范围内x 的取值范围，然后根据终边相同角的同名三角函数值相等，写出原不等式的解集．跟踪训练2 根据余弦曲线求满足cos x ≤12的x 的取值范围．解析：作出余弦函数y ＝cos x ，x ∈[0,2π]的图象，如图所示，由图象可以得到满足条件的x 的集合为[π3＋2k π，5π3＋2k π]，k ∈Z .在同一坐标内作y ＝cos x 与y ＝12的图象，利用图象求x 的范围.1.4.1-2.1[基础巩固](25分钟，60分)一、选择题(每小题5分，共25分)1．下列对函数y ＝cos x 的图象描述错误的是( ) A ．在[0,2π]和[4π，6π]上的图象形状相同，只是位置不同 B ．介于直线y ＝1与直线y ＝－1之间 C ．关于x 轴对称 D ．与y 轴只有一个交点解析：观察余弦函数的图象知：y ＝cos x 关于y 轴对称，故C 错误． 答案：C2．下列各点中，不在y ＝sin x 图象上的是( ) A ．(0,0) B.⎝ ⎛⎭⎪⎫π2，1C.⎝⎛⎭⎪⎫3π2，－1 D ．(π，1) 解析：y ＝sin x 图象上的点是(π，0)，而不是(π，1)． 答案：D3．不等式sin x >0，x ∈[0,2π]的解集为( ) A ．[0，π] B ．(0，π)C.⎣⎢⎡⎦⎥⎤π2，3π2D.⎝ ⎛⎭⎪⎫π2，3π2解析：由y ＝sin x 在[0,2π]的图象可得． 答案：B 4．点M ⎝⎛⎭⎪⎫π2，－m 在函数y ＝sin x 的图象上，则m 等于( )A ．0B ．1C ．－1D ．2解析：点M 在y ＝sin x 的图象上，代入得－m ＝sin π2＝1，∴m ＝－1.答案：C5．在同一平面直角坐标系内，函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象( )A ．重合B ．形状相同，位置不同C ．关于y 轴对称D ．形状不同，位置不同解析：根据正弦曲线的作法过程，可知函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象位置不同，但形状相同．答案：B二、填空题(每小题5分，共15分) 6．下列叙述正确的有________．(1)y ＝sin x ，x ∈[0,2π]的图象关于点P (π，0)成中心对称； (2)y ＝cos x ，x ∈[0,2π]的图象关于直线x ＝π成轴对称； (3)正弦、余弦函数的图象不超过直线y ＝1和y ＝－1所夹的范围．解析：分别画出函数y ＝sin x ，x ∈[0,2π]和y ＝cos x ，x ∈[0,2π]的图象，由图象观察可知(1)(2)(3)均正确．答案：(1)(2)(3)7．关于三角函数的图象，有下列说法： (1)y ＝sin|x |与y ＝sin x 的图象关于y 轴对称； (2)y ＝cos(－x )与y ＝cos|x |的图象相同；(3)y ＝|sin x |与y ＝sin(－x )的图象关于x 轴对称； (4)y ＝cos x 与y ＝cos(－x )的图象关于y 轴对称． 其中正确的序号是________．解析：对(2)，y ＝cos(－x )＝cos x ，y ＝cos|x |＝cos x ，故其图象相同； 对(4)，y ＝cos(－x )＝cos x ，故其图象关于y 轴对称，由作图可知(1)(3)均不正确． 答案：(2)(4)8．直线y ＝12与函数y ＝sin x ，x ∈[0,2π]的交点坐标是________．解析：令sin x ＝12，则x ＝2k π＋π6或x ＝2k π＋56π，又∵x ∈[0,2π]，故x ＝π6或56π.答案：⎝ ⎛⎭⎪⎫π6，12，⎝ ⎛⎭⎪⎫56π，12三、解答题(每小题10分，共20分)9．利用“五点法”作出函数y ＝1－sin x (0≤x ≤2π)的简图． 解析：(1)取值列表：(2)10．根据y ＝cos x 的图象解不等式：－32≤cos x ≤12，x ∈[0,2π]． 解析：函数y ＝cos x ，x ∈[0,2π]的图象如图所示：根据图象可得不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪π3≤x ≤5π6或7π6≤x ≤5π3. [能力提升](20分钟，40分)11．已知函数y ＝2cos x (0≤x ≤2π)的图象和直线y ＝2围成一个封闭的平面图形，则这个封闭图形的面积为( )A ．4B ．8C ．2πD ．4π解析：依题意，由余弦函数图象关于点⎝ ⎛⎭⎪⎫π2，0和点⎝ ⎛⎭⎪⎫3π2，0成中心对称，可得y ＝2cosx (0≤x ≤2π)的图象和直线y ＝2围成的封闭图形的面积为2π×2＝4π.答案：D12．函数y ＝2cos x －2的定义域是________． 解析：要使函数有意义，只需2cos x －2≥0，即cos x ≥22.由余弦函数图象知(如图)，所求定义域为⎣⎢⎡⎦⎥⎤－π4＋2k π，π4＋2k π，k ∈Z .答案：⎣⎢⎡⎦⎥⎤－π4＋2k π，π4＋2k π，k ∈Z 13．利用“五点法”作出y ＝sin ⎝⎛⎭⎪⎫x －π2⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤π2，52π的图象．解析：列表如下：14．利用图象变换作出下列函数的简图：(1)y＝1－cos x，x∈[0,2π]；(2)y＝|sin x|，x∈[0,4π]．解析：(1)首先用“五点法”作出函数y＝cos x，x∈[0,2π]的简图，再作出y＝cos x，x∈[0,2π]的简图关于x轴对称的简图，即y＝－cos x，x∈[0,2π]的简图，将y＝－cos x，x∈[0,2π]的简图向上平移1个单位即可得到y＝1－cos x，x∈[0,2π]的简图，如图所示．(2)首先用“五点法”作出函数y＝sin x，x∈[0,4π]的简图，再将该简图在x轴下方的部分翻折到x轴的上方，即得到y＝|sin x|，x∈[0,4π]的简图，如图所示．。

第十一课正弦、余弦函数的图象3.余弦函数图象画法由诱导公式可知：y ＝cos x ＝sin(2π＋x )＝sin(x ＋2π)，余弦函数y ＝cos x ， x ∈R 与函数y ＝sin(x ＋2π)，x ∈R 是同一个函数.而y ＝sin(x ＋2π)，x ∈R 的图象可通过将正弦曲线向左平行移动2π个单位长度而得到. 二、合作探究1. 用“五点(画图)法〞作函数的图象例1 用“五点法〞作出函数1sin y x =-，[0,2]x π∈的图象.【思路分析】根据“五点法〞作图的步骤,先列表,后描点,最后用平滑的曲线连接起来.【解析】按五个关键点列表:x0 2π π 23π 2π sin x0 1 0 －1 0 1－sin x 1 0 1 2 1在直角坐标系中描出以下五点〔0，1〕，〔2π，0〕，〔π，1〕，〔23π，2〕，〔2π，1〕如下图.然后用光滑的曲线顺次连接起来，就得到函数y =1－sin x ,x ∈［0,2π］图象的简图.【点评】作函数y =1－sin x ,x ∈R 的简图时分两个步骤进行：〔1〕先作出［0,2π］上的简图，〔2〕再根据终边相同角的三角函数值相等，将［0, 2π］上的简图依次向左、右平移.假设从y =sin x ,x ∈［0,2π］与y =1－sin x ,x ∈［0,2π］图象间的关系考查，要得到所作函数图象，只需作y ＝sin x ，x ∈［0，2π］的图象关于x 轴的对称图象，再将所得图象向上平移一个单位，这也是五点作图的依据所在.☆自主探究1. 用“五点法〞作出函数sin 3y x π⎛⎫=+ ⎪⎝⎭，[0,2]x π∈的简图.四、总结提升总结：y ＝sin x ，x ∈［0，2π］的图象上，起着关键作用的点只有以下五个： (0，0)，(2π，1)，(π，0)，(π，－1)，(2π，0)因材施教：教学后记：。

课题：正弦函数、余弦函数的单调性教材：人教版必修4（新课标A 版）教学目标：知识目标： 掌握正弦函数和余弦函数的单调性；会运用正余弦函数的单调性去判断两个同名的弦函数值的大小关系；能求出求形如的单调区间及)cos()sin(ϕωϕω+=+=x y x y 。

情感目标： 通过经历新知识的探索，培养学生善观察、勤思考、爱探究良好的学习品质。

能力目标： 培养学生的思考分析能力、自主探究能力，提高学生对新旧知识的运用能力，在推导新知及解题过程中使学生感悟数形结合思想及化归思想。

教学重点、难点：教学重点：用数形结合法探索正、余弦函数的单调性。

教学难点：求形如情形的单调区间当及0)cos()sin(>+=+=ωϕωϕωx y x y 。

教学方法：讲授法，探究法，讲练结合法教学过程:一、复习引入:1引入：前面已学过正弦函数和余弦函数的图象以及它们周期性和奇偶性，（投影：正、余弦函数的图象），现在我们要通过正弦、余弦函数图象去研究它的另一个重要的性质——单调性。

2、板书课题：正弦函数、余弦函数的单调性3、回忆：函数在某区间上单调增（或单调减）的图象特征。

二、新课:（一）、正弦函数的单调性1、探究正弦函数]23,2[sin ππ-=在x y 上的单调性(1) 让学生观察正弦函数y=sinx 的图象启发学生思考：它有多段图象自左到右是呈现上升状态，也有多段呈下降状态，根据函数单调性知识可知它分段具有单调性，那么这里面有什么规律呢，先要找一个周期区间上的函数图象来分析研究。

引导学生分析所选用的那一个区间段的图是否最佳选择，最适合的是只有一个单调增区间和单调减区间的用这两段上的图象。

（选择区间]23,2[ππ-） (2)让学生再观察正弦函数在区间]23,2[ππ-上的图象的升降情况.提问：从图形中你发现了什么样的现象？（3）总结出y=sinx 在一个周期段的区间上的单调性结论:(投影)正弦函数y=sinx 在闭区间]2,2[ππ-上单调增,其值由-1增大到1; 在闭区间]23,2[ππ上单调减,其值由1减小到-1. 2、探讨正弦函数y=sinx 在整个定义域上的单调性（1）观察y=sinx 在闭区间⋯⋯--]2325[]25,23[ππππ，、，它们的图象是完全相同的，也一样是从左到右上升状态，这些闭区间之间的关系是相隔了整数倍的周期，引导结合正弦函数的周期性,让学生试写出它在定义域上的单调增区间（2）得出结论:正弦函数y=sinx 在每一个闭区间)](22,22[Z k k k ∈+-ππππ上单调增,其值由-1增大到1;用类似方法探索出正弦函数y=sinx 在定义域上的减区间，得到结论：在每一个闭区间)](232,22[Z k k k ∈++ππππ上单调减,其值由1减小到-1. （教师板书正弦函数的增、减区间）强调：正弦函数在定义域R 上不单调，但在各个周期上分段单调；上面写的正弦函数的增、减区间，其实是由很多个区间组成，并不止一个，因为k 每取一个整数就有一个相应的区间，书写带周期的单调区间时，勿忘了写上Z k ∈这一条件。

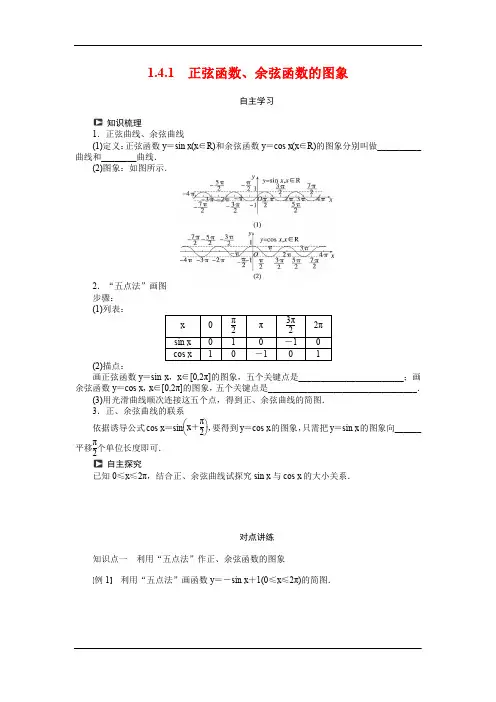
1.4.1 正弦函数、余弦函数的图象自主学习知识梳理1．正弦曲线、余弦曲线 (1)定义：正弦函数y ＝sin x (x ∈R)和余弦函数y ＝cos x (x ∈R)的图象分别叫做__________曲线和________曲线．(2)图象：如图所示．2．“五点法”画图 步骤： (1)列表：(2)描点：画正弦函数y ＝sin x ，x ∈[0,2π]的图象，五个关键点是________________________；画余弦函数y ＝cos x ，x ∈[0,2π]的图象，五个关键点是__________________________________．(3)用光滑曲线顺次连接这五个点，得到正、余弦曲线的简图． 3．正、余弦曲线的联系依据诱导公式cos x ＝sin ⎝⎛⎭⎫x ＋π2，要得到y ＝cos x 的图象，只需把y ＝sin x 的图象向______平移π2个单位长度即可．自主探究已知0≤x ≤2π，结合正、余弦曲线试探究sin x 与cos x 的大小关系．对点讲练知识点一 利用“五点法”作正、余弦函数的图象例1 利用“五点法”画函数y ＝－sin x ＋1(0≤x ≤2π)的简图．回顾归纳作正弦、余弦曲线要理解几何法作图，掌握五点法作图．“五点”即y＝sin x或y＝cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点．“五点法”是作简图的常用方法．变式训练1利用“五点法”画函数y＝－1－cos x，x∈[0,2π]的简图．知识点二利用三角函数图象求定义域例2求函数f(x)＝lg sin x＋16－x2的定义域．回顾归纳一些三角函数的定义域可以借助函数图象直观地观察得到，同时要注意区间端点的取舍．变式训练2求函数f(x)＝cos x＋lg(8x－x2)的定义域．知识点三利用三角函数的图象判断方程解的个数例3在同一坐标系中，作函数y＝sin x和y＝lg x的图象，根据图象判断出方程sin x ＝lg x的解的个数．回顾归纳三角函数的图象是研究函数的重要工具，通过图象可较简便的解决问题，这正是数形结合思想方法的应用．变式训练3求方程x2＝cos x的实数解的个数．1．正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用，是运用数形结合思想解决三角函数问题的基础．2．五点法是画三角函数图象的基本方法，要熟练掌握，与五点法作图有关的问题是高考常考知识点之一.课时作业一、选择题1．函数y ＝sin x (x ∈R)图象的一条对称轴是( ) A ．x 轴 B ．y 轴C ．直线y ＝xD ．直线x ＝π22．函数y ＝－cos x 的图象与余弦函数y ＝cos x 的图象( ) A ．只关于x 轴对称 B ．关于原点对称 C ．关于原点、x 轴对称 D ．关于原点、坐标轴对称3．如果x ∈[0,2π]，则函数y ＝sin x ＋－cos x 的定义域为( )A ．[0，π] B.⎣⎡⎦⎤π2，3π2 C.⎣⎡⎦⎤π2，π D.⎣⎡⎦⎤3π2，2π 4．在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4，3π4 B.⎝⎛⎦⎤π4，π2∪⎝⎛⎦⎤5π4，3π2 C.⎝⎛⎭⎫π4，π2 D.⎝⎛⎭⎫5π4，7π4 5．已知函数y ＝2sin x ⎝⎛⎭⎫π2≤x ≤5π2的图象与直线y ＝2围成一个封闭的平面图形，那么此封闭图形的面积( )A ．4B ．8C ．4πD ．2π二、填空题6．函数y ＝cos x1＋sin x的定义域为____________．7．函数y ＝2cos x ＋1的定义域是______________．8．设0≤x ≤2π，且|cos x －sin x |＝sin x －cos x ，则x 的取值范围为________．三、解答题9．利用“五点法”作出下列函数的简图：(1)y ＝－sin x (0≤x ≤2π)；(2)y ＝1＋cos x (0≤x ≤2π)．10．分别作出下列函数的图象．(1)y ＝|sin x |，x ∈R ；(2)y ＝sin|x |，x ∈R.§1.4 三角函数的图象与性质 1．4.1 正弦函数、余弦函数的图象答案知识梳理1．(1)正弦 余弦2．(2)(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0) (0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1) 3．左 自主探究解 正、余弦曲线如图所示．由图象可知①当x ＝π4或x ＝5π4时，sin x ＝cos x ，②当π4<x <5π4时，sin x >cos x .③当0≤x <π4或5π4<x ≤2π时，sin x <cos x .对点讲练例1 解 利用“五点法”作图 取值列表：x 0 π2π 3π2 2π sin x 0 1 0－1 0 1－sin x1 0 1 21变式训练1 x0 π2 π 3π2 2π cos x 1 0 －1 0 1 －1－cos x－2－1－1－2例2 解 由题意，x 满足不等式组⎩⎪⎨⎪⎧sin x >016－x 2≥0， 即⎩⎪⎨⎪⎧－4≤x ≤4sin x >0，作出y ＝sin x 的图象，如图所示．结合图象可得：x ∈[－4，－π)∪(0，π)．变式训练2 解 由⎩⎪⎨⎪⎧ 8x －x 2>0cos x ≥0，得⎩⎪⎨⎪⎧0<x <8cos x ≥0.画出y ＝cos x ，x ∈[0,3π]的图象，如图所示．结合图象可得：x ∈⎝⎛⎦⎤0，π2∪⎣⎡⎦⎤3π2，5π2.例3 解 建立坐标系xOy ，先用五点法画出函数y ＝sin x ，x ∈[0,2π]的图象，再依次向左、右连续平移2π个单位，得到y ＝sin x 的图象．描出点⎝⎛⎭⎫110，－1，(1,0)，(10,1)并用光滑曲线连接得到y ＝lg x 的图象，如图所示．由图象可知方程sin x ＝lg x 的解有3个．变式训练3 解 作函数y ＝cos x 与y ＝x 2的图象，如图所示， 由图象，可知原方程有两个实数解．课时作业 1．D2．C [结合图象易知．]3．C [∵sin x ≥0且－cos x ≥0，∴x ∈⎣⎡⎦⎤π2，π.] 4．A[∵sin x >|cos x |，∴sin x >0，∴x ∈(0，π)，在同一坐标系中画出y ＝sin x ，x ∈(0，π)与y ＝|cos x |，x ∈(0，π)的图象，观察图象易得x ∈⎝⎛⎭⎫π4，3π4.] 5．C [数形结合，如图所示．y ＝2sin x ，x ∈⎣⎡⎦⎤π2，5π2的图象与直线y ＝2围成的封闭平面图形面积相当于由x ＝π2，x ＝5π2， y ＝0，y ＝2围成的矩形面积，即S ＝⎝⎛⎭⎫5π2－π2×2＝4π.] 6.⎝⎛⎦⎤－π2＋2k π，π2＋2k π (k ∈Z) 解析 x 应满足：⎩⎪⎨⎪⎧1＋sin x ≠0⇒sin x ≠－1，cos x ≥0，综合正、余弦函数图象可知：－π2＋2k π<x ≤π2＋2k π. 7.⎣⎡⎦⎤2k π－2π3，2k π＋2π3 ，(k ∈Z) 解析 由2cos x ＋1≥0，得cos x ≥－12，∴2k π－2π3≤x ≤2k π＋2π3，k ∈Z.8.⎣⎡⎦⎤π4，5π4解析 由题意知sin x －cos x ≥0，即cos x ≤sin x ，在同一坐标系画出y ＝sin x ，x ∈[0,2π] 与y ＝cos x ，x ∈[0,2π]的图象，如图所示：观察图象得：π4≤x ≤5π4.9．解 利用“五点法”作图． (1)列表：x0 π2 π 3π2 2π sin x 0 1 0 －1 0 －sin x－11(2)列表：x0 π2 π 3π2 2π cos x 1 0 －1 0 1 1＋cos x211210．解 (1)y ＝|sin x |＝⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π＋π)－sin x (2k π＋π<x ≤2k π＋2π)(k ∈Z)．其图象如图所示，(2)y ＝sin|x |＝⎩⎪⎨⎪⎧sin x (x ≥0)－sin x (x <0)，其图象如图所示，。

1.4.2 正弦函数、余弦函数的性质(二)自主学习知识梳理自主探究正弦曲线与余弦曲线都既是轴对称图形又是中心对称图形，那么：(1)正弦函数y ＝sin x 的对称轴方程是______________，对称中心坐标是______________．(2)余弦函数y ＝cos x 的对称轴方程是______________，对称中心坐标是______________．对点讲练知识点一 求正、余弦函数的单调区间例1 求函数y ＝sin ⎝⎛⎭⎫π3－2x 的单调递减区间．回顾归纳 求y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)的单调区间时，如果式子中x 的系数为负数，先利用诱导公式将x 的系数变为正数再求其单调区间．变式训练1 求函数y ＝2cos ⎝⎛⎭⎫π4－x 2的单调增区间．知识点二 比较三角函数值的大小例2 利用三角函数的单调性，比较下列各组数的大小．(1)sin 196°与cos 156°；(2)sin 1，sin 2，sin 3.回顾归纳 用正弦函数和余弦函数的单调性来比较大小时，应先将异名化同名，再将不是同一单调区间的角用诱导公式转化到同一单调区间，再利用单调性来比较大小．变式训练2 比较下列各组数的大小．(1)cos 870°，cos 890°；(2)sin ⎝⎛⎭⎫－37π6，sin 49π3.知识点三 正、余弦函数的最值问题例3 已知函数f (x )＝2a sin ⎝⎛⎭⎫2x －π3＋b 的定义域为⎣⎡⎦⎤0，π2，最大值为1，最小值为－5，求a 和b 的值．回顾归纳 此类问题应特别注意正、余弦函数值域的有界性，即当x ∈R 时，－1≤sin x ≤1，－1≤cos x ≤1，另外还应注意定义域对值域的影响．变式训练3 若函数y ＝a －b cos x (b >0)的最大值为32，最小值为－12，求函数y ＝－4a cosbx 的最值和最小正周期．1．求函数y ＝A sin(ωx ＋φ) (A >0，ω>0)单调区间的方法是：把ωx ＋φ看成一个整体，由2k π－π2≤ωx ＋φ≤2k π＋π2(k ∈Z )解出x 的范围，所得区间即为增区间，由2k π＋π2≤ωx ＋φ≤2k π＋3π2(k ∈Z )解出x 的范围，所得区间即为减区间．若ω<0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．2．比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断．3．求三角函数值域或最值的常用求法(1)将y 表示成以sin x (或cos x )为元的一次或二次等复合函数再利用换元或配方、或利用函数的单调性等来确定y 的范围．(2)将sin x 或cos x 用所求变量y 来表示，如sin x ＝f (y )，再由|sin x |≤1，构建关于y 的不等式|f (y )|≤1，从而求得y 的取值范围.课时作业一、选择题1．若y ＝sin x 是减函数，y ＝cos x 是增函数，那么角x 在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．函数y ＝sin ⎝⎛⎭⎫x －π2 (x ∈k )在( ) A ．[0，π]上是增函数 B.⎣⎡⎦⎤－π2，π2上是增函数 C ．[0，π]上是减函数 D.⎣⎡⎦⎤－π2，π2上是减函数 3．当－π2≤x ≤π2时，函数f (x )＝2sin ⎝⎛⎭⎫x ＋π3有( ) A ．最大值为1，最小值为－1B ．最大值为1，最小值为－12C ．最大值为2，最小值为－2D ．最大值为2，最小值为－14．函数y ＝sin(x ＋φ)的图象关于y 轴对称，则φ的一个取值是( ) A.π2 B ．－π4C ．π B ．2π 5．函数y ＝sin 2x ＋sin x －1的值域为( )A.[]－1，1B.⎣⎡⎦⎤－54，－1 C.⎣⎡⎦⎤－54，1 D.⎣⎡⎦⎤－1，54二、填空题6．函数y ＝sin(π＋x )，x ∈⎣⎡⎦⎤－π2，π的单调增区间是________________． 7．函数y ＝log 12(1＋λcos x )的最小值是－2，则λ的值是________．8．函数y ＝－cos 2x ＋cos x (x ∈R )的值域是________．三、解答题9．求下列函数的单调增区间．(1)y ＝1－sin x 2； (2)y ＝log 12(cos 2x )．10．求下列函数的值域．(1)y ＝1－2cos 2x ＋2sin x ； (2)y ＝2－sin x2＋sin x.1.4.2 正弦函数、余弦函数的性质(二)答案(1)x ＝k π＋π2(k ∈Z ) (k π，0) (k ∈Z )(2)x ＝k π (k ∈Z ) ⎝⎛⎭⎫k π＋π2，0 (k ∈Z ) 对点讲练例1 解 由已知函数为y ＝－sin ⎝⎛⎭⎫2x －π3，则欲求函数的单调递减区间，只需求y ＝sin ⎝⎛⎭⎫2x －π3的单调递增区间． 由－π2＋2k π≤2x －π3≤π2＋2k π (k ∈Z )，解得－π12＋k π≤x ≤5π12＋k π (k ∈Z )．∴函数的单调递减区间为⎣⎡⎦⎤－π12＋k π，5π12＋k π (k ∈Z )． 变式训练1 解 y ＝2cos ⎝⎛⎭⎫π4－x 2＝2cos ⎝⎛⎭⎫x 2－π4.由2k π－π≤x 2－π4≤2k π，k ∈Z ，解得2k π－3π4≤x 2≤2k π＋π4，k ∈Z .即4k π－3π2≤x ≤4k π＋π2，k ∈Z ，∴函数的单调增区间是⎣⎡⎤4k π－3π2，4k π＋π2 (k ∈Z )． 例2 解 (1)sin 196°＝sin(180°＋16°)＝－sin 16°， cos 156°＝cos(180°－24°)＝－cos 24°＝－sin 66°， ∵0°<16°<66°<90°，∴sin 16°<sin 66°.从而－sin 16°>－sin 66°，即sin 196°>cos 156°.(2)∵1<π2<2<3<π，sin(π－2)＝sin 2，sin(π－3)＝sin 3.0<π－3<1<π－2<π2且y ＝sin x 在⎝⎛⎭⎫0，π2上递增， ∴sin(π－3)<sin 1<sin(π－2)， 即sin 3<sin 1<sin 2.变式训练2 解 (1)cos 870°＝cos(2×360°＋150°)＝cos 150°， cos 890°＝cos(2×360°＋170°)＝cos 170°， ∵余弦函数y ＝cos x 在[0°，180°]上是减函数， ∴cos 150°>cos 170°，即cos 870°>cos 890°.(2)sin ⎝⎛⎭⎫－37π6＝sin ⎝⎛⎭⎫－6π－π6＝sin ⎝⎛⎭⎫－π6， sin 49π3＝sin ⎝⎛⎭⎫16π＋π3＝sin π3， ∵正弦函数y ＝sin x 在⎣⎡⎦⎤－π2，π2上是增函数， ∴sin ⎝⎛⎭⎫－π6<sin π3，即sin ⎝⎛⎭⎫－37π6<sin 49π3. 例3 解 ∵0≤x ≤π2，∴－π3≤2x －π3≤2π3，∴－32≤sin ⎝⎛⎭⎫2x －π3≤1，易知a ≠0. 当a >0时，f (x )max ＝2a ＋b ＝1， f (x )min ＝－3a ＋b ＝－5.由⎩⎨⎧ 2a ＋b ＝1－3a ＋b ＝－5，解得⎩⎨⎧a ＝12－63b ＝－23＋123. 当a <0时，f (x )max ＝－3a ＋b ＝1， f (x )min ＝2a ＋b ＝－5.由⎩⎨⎧ －3a ＋b ＝12a ＋b ＝－5，解得⎩⎨⎧a ＝－12＋63b ＝19－123. 变式训练3 解 ∵y ＝a －b cos x (b >0)，∴y max ＝a ＋b ＝32，y min ＝a －b ＝－12.由⎩⎨⎧a ＋b ＝32a －b ＝－12，解得⎩⎪⎨⎪⎧a ＝12b ＝1.∴y ＝－4a cos bx ＝－2cos x ， ∴y max ＝2，y min ＝－2，T ＝2π. 课时作业 1．C 2.A3．D [∵－π2≤x ≤π2，∴－π6≤x ＋π3≤5π6.∴当x ＋π3＝－π6，即x ＝－π2时，f (x )有最小值－1.当x ＋π3＝π2，即x ＝π6时，f (x )有最大值2.]4．A [若y ＝sin(x ＋φ)的图象关于y 轴对称．则φ＝k π＋π2，∴当k ＝0时，φ＝π2.]5．C [y ＝sin 2x ＋sin x －1＝⎝⎛⎭⎫sin x ＋122－54 ∵－1≤sin x ≤1，∴当sin x ＝－12时，y 取最小值－54，当sin x ＝1时，y 取最大值1.] 6.⎣⎡⎦⎤π2，π 7．±3解析 由题意，1＋λcos x 的最大值为4， 当λ>0时，1＋λ＝4，λ＝3； 当λ<0时，1－λ＝4，λ＝－3. ∴λ＝±3.8.⎣⎡⎦⎤－2，14 解析 y ＝－⎝⎛⎭⎫cos x －122＋14 ∵－1≤cos x ≤1，∴当cos x ＝12时，y max ＝14.当cos x ＝－1时，y min ＝－2.∴函数y ＝－cos 2x ＋cos x 的值域是⎣⎡⎦⎤－2，14. 9．解 (1)由2k π＋π2≤x 2≤2k π＋32π，k ∈Z ，得4k π＋π≤x ≤4k π＋3π，k ∈Z .∴y ＝1－sin x2的增区间为[4k π＋π，4k π＋3π] (k ∈Z )．(2)由题意得cos 2x >0且cos 2x 递减．∴x 只须满足：2k π<2x <2k π＋π2，k ∈Z .∴k π<x <k π＋π4，k ∈Z .∴y ＝log 12(cos 2x )的增区间为⎝⎛⎭⎫k π，k π＋π4，k ∈Z . 10．解 (1)y ＝1－2cos 2x ＋2sin x ＝2sin 2x ＋2sin x －1＝2⎝⎛⎭⎫sin x ＋122－32 当sin x ＝－12时，y min ＝－32；当sin x ＝1时，y max ＝3.∴函数y ＝1－2cos 2x ＋2sin x 的值域为⎣⎡⎦⎤－32，3. (2)方法一 y ＝4－(2＋sin x )2＋sin x ＝42＋sin x－1∵－1≤sin x ≤1，∴1≤2＋sin x ≤3， ∴13≤12＋sin x ≤1，∴43≤42＋sin x ≤4， ∴13≤42＋sin x －1≤3，即13≤y ≤3.∴函数y ＝2－sin x 2＋sin x的值域为⎣⎡⎦⎤13，3. 方法二 由y ＝2－sin x 2＋sin x ，解得sin x ＝2－2yy ＋1，由|sin x |≤1，得⎪⎪⎪⎪⎪⎪2－2y y ＋1≤1，∴(2－2y )2≤(y ＋1)2， 整理得3y 2－10y ＋3≤0，解得13≤y ≤3.∴函数y ＝2－sin x 2＋sin x 的值域为⎣⎡⎦⎤13，3.。