材料力学第七章作业参考答案

250
−qx l⎞ ⎛ 9l 3 − 24lx 2 + 16 x 3 ) ⎜ 0 ≤ x ≤ ⎟ ( 384 EJ 2⎠ ⎝ − ql ⎛l ⎞ y2 = −l 3 + 17l 2 x − 24lx 2 + 8 x 3 ) ⎜ ≤ x ≤ l ⎟ ( 384 EJ ⎝2 ⎠
y1 =
41ql 4 ( x = 0.25l ) 1536 EJ 5ql 4 ⎛l⎞ y⎜ ⎟ = − 768EJ ⎝2⎠
习 题 7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI为常量。
7－1 （a） M( x) = M 0
∴ EJy '' = M 0 1 EJy ' = M 0 x + C EJy = M 0 x 2 + Cx + D 2 边界条件: x = 0 时 y = 0 ； y' = 0
代入上面方程可求得：C=D=0
（c）
l−x q0 l q0 1 3 ⎛l−x⎞ M ( x) = − q( x) ( l − x ) ⎜ ⎟ = − ( l − x) 2 6l ⎝ 8 ⎠ q 3 ∴ EJy '' = 0 ( l − x ) 6l q 4 EJy ' = − 0 ( l − x ) + C 24l q 5 EJy = 0 ( l − x ) + Cx + D 120l y = 0 ； y' = 0 边界条件： x = 0 时 q( x) =
）
（c）解：
q0 x l q x2 EJy ''' = 0 + C 2l q0 x3 '' EJy = + Cx + D 6l q x 4 Cx 2 EJy ' = 0 + + Dx + A 24l 2 q0 x5 Cx 3 Dx 2 ' EJy = + + + Ax + B 120l 6 2 ⎧y=0 ⎧y=0 边界条件： x = 0 ⎨ '' x = l ⎨ '' ⎩y = 0 ⎩y = 0 ql D=0 ∴C = − 0 6 7q l 3 A= 0 B=0 360 EJy '''' =

3．确定积分常数
(a) (b)
7
该梁的位移边界条件为：
在x 0处， w0 dw 在x 0处， 0 dx 将条件(c)与(d)分别代入式(b)和(a)，得 D 0，C 0 4．建立挠曲轴方程 将所得 C 与 D 值代入式(b)，得挠曲轴的通用方程为
1 Fa 2 F 3 3Fa [ x x xa EI 4 6 4 由此得 AC 段、 CD 段和 DB 段的挠曲轴方程依次为 w
5．计算 wC 和 θ B 将 x a 代入上述 w1或w2 的表达式中，得截面 C 的挠度为
41qa 4 ( ) 240EI 将以上所得 C 值和 x 2a 代入式(a)，得截面 B 的转角为 wC θB qa 3 7 4 16 1 187 203qa 3 [ ] EI 24 24 24 720 720 EI ()
(4)
D1 0 ， C1
由条件（4） 、式（a）与（c） ，得
qa 3 12 EI
C2
由条件（3） 、式（b）与（d） ，得
qa 3 3EI
D2
7qa 4 24 EI
3. 计算截面 C 的挠度与转角 将所得积分常数值代入式（c）与（d） ，得 CB 段的转角与挠度方程分别为
q 3 qa 3 x2 6 EI 3EI 3 q qa 7 qa 4 4 w2 x2 x2 24 EI 3EI 24 EI 将 x2=0 代入上述二式，即得截面 C 的转角与挠度分别为
5．计算 wC 和 θ B 将 x a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
Fa 3 ( ) 12 EI 将以上所得 C 值和 x 3a 代入式(a)，得截面 B 的转角为 wC

第七章应力状态与强度理论一、教学目标和教学内容1．教学目标通过本章学习，掌握应力状态的概念及其研究方法；会从具有受力杆件中截取单元体并标明单元体上的应力情况；会计算平面应力状态下斜截面上的应力；掌握平面应力状态和特殊空间应力状态下的主应力、主方向的计算，并会排列主应力的顺序；掌握广义胡克定律；了解复杂应力状态比能的概念；了解主应力迹线的概念。

掌握强度理论的概念。

了解材料的两种破坏形式（按破坏现象区分）。

了解常用的四个强度理论的观点、破坏条件、强度条件。

掌握常用的四个强度理论的相当应力。

了解莫尔强度理论的基本观点。

会用强度理论对一些简单的杆件结构进行强度计算。

2．教学内容○1应力状态的概念；○2平面应力状态分析；○3三向应力状态下的最大应力；○4广义胡克定律•体应变；○5复杂应力状态的比能；⑥梁的主应力•主应力迹线的概念。

讲解强度理论的概念及材料的两种破坏形式。

讲解常用的四个强度理论的基本观点，并推导其破坏条件从而建立强度计算方法。

介绍几种强度理论的应用范围和各自的优缺点。

简单介绍莫尔强度理论。

二、重点难点重点：1、平面应力状态下斜截面上的应力计算，主应力及主方向的计算，最大剪应力的计算。

2、广义胡克定律及其应用。

难点：1、应力状态的概念，从具体受力杆件中截面单元体并标明单元体上的应力情况。

2、斜截面上的应力计算公式中关于正负符号的约定。

3、应力主平面、主应力的概念，主应力的大小、方向的确定。

4、广义胡克定律及其应用。

5 强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。

6 常用四个强度理论的理解。

7 危险点的确定及其强度计算。

三、教学方式采用启发式教学，通过提问，引导学生思考，让学生回答问题。

四、建议学时10学时五、讲课提纲1、应力状态的概念所谓“应力状态”又称为一点处的应力状态（state of stresses at a given point）,是指过一点不同方向面上应力的集合。

第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。

(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说确的是（ B ）。

第七章习题7-1 直径d=2cm的拉伸试件，当与杆轴成斜截面上的切应力时，杆表面上将出现滑移线。

求此时试件的拉力P。

7-2在拉杆的某一斜截面上，正应力为，切应力为。

试求最大正应力和最大切应力。

7-3 已知应力状态如图a、b、c所示，求指定斜截面ab上的应力，并画在单元体上。

7-4已知应力状态如图a、b、c所示，求指定斜截面ab上的应力，并画在单元体上。

7-5求图示各单元体的三个主应力，最大切应力和它们的作用面方位，并画在单元体图上。

7-6 已知一点为平面应力状态，过该点两平面上的应力如图所示，求及主应力、主方向和最大切应力。

7-7 一圆轴受力如图所示，已知固定端横截面上的最大弯曲应力为40MPa，最大扭转切应力为30 Mpa，因剪力而引起的最大切应力为6kPa.（1）用单元体画出在A、B、C、D各点处的应力状态；（2）求A点的主应力和最大切应力以及它们的作用面的方位。

7-8 求图示各应力状态的主应力、最大切应力以及它们的作用面的方位。

7-9 设地层为石灰岩，波松比，单位体积重。

试计算离地面400m深处的压应力。

7-10 图示一钢制圆截面轴，直径d=60mm,材料的弹性模量E=210Gpa。

波松比，用电测法测得A点与水平面成方向的线应变，求轴受的外力偶矩m。

7-11 列车通过钢桥时，在大梁侧表面某点测得x和y向的线应变，材料的弹性模量E=200Gpa，波松比，求该点x、y面的正应力和。

7-12 铸铁薄壁管如图所示，管的外直径D=200mm,壁厚t=15mm，内压p=4MPa,轴向压力P=200Kn，许用应力，波松比，试用第二强度理论校核该管的强度。

7-13 薄壁锅炉的平均直径为1250mm，最大内压为23个大气压（1大气压0.1MPa），在高温下工作，屈服点。

若安全系数为1.8，试按第三、第四强度理论设计锅炉的壁厚。

参考答案7-2解已知：解：7-3 （a）解已知：=0(b) 解已知：=0解(c) 解已知：解：7-4(a) 解已知：解：(b) 解已知：(c) 解已知：解：7-57-6 已知一点为平面应力状态，过该点两平面上的应力如图所示，求及主应力、主方向和最大切应力。

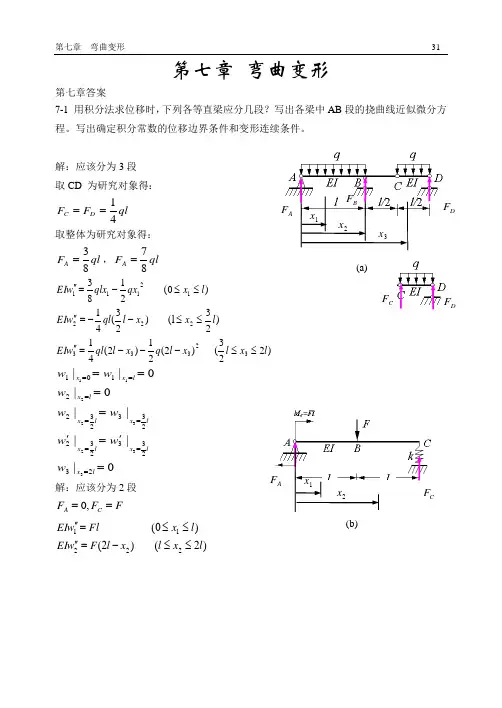
第七章 弯曲变形第七章答案7-1 用积分法求位移时，下列各等直梁应分几段？写出各梁中AB 段的挠曲线近似微分方程。

写出确定积分常数的位移边界条件和变形连续条件。

解：应该分为3段 取CD 为研究对象得：ql F F D C 41==取整体为研究对象得：ql F A 83=，ql F A 87= )223( )2(21)2(41)23(l )23(41)(0 21833233322212111l x l x l q x l ql w EI l x x l ql w EI l x qx qlx w EI ≤≤---=''≤≤--=''≤≤-=''0|||||0|0||23233232233232210133232211='='============l x lx lx lx lx l x l x x w w w w w w w w解：应该分为2段F F F C A ==,0)2( )2()(0 22211l x l x l F w EI l x Fl w EI ≤≤-=''≤≤=''1x x AF DF BF DF(b)AF 1xkFw w w w w w l x l x l x l x l x x -='='========22212101232321|||||0| 7.2 用积分法求图示梁跨度中点的挠度c w 和端截面转角A θ及B θ。

（EI ql w C 76854=，EI ql A 38473=θ，EI ql B 12833-=θ）解：ql F A 81=；ql F B 83=1113111211111 481 161)2(0 81D x C qlx EIw C qlx w EI l x qlx w EI ++=+='≤≤='' 2224232223222222222 )2(241 481 )2(61 161)2( )2(21 81D x C l x q qlx EIw C l x q qlx w EI l x l l x q qlx w EI ++--=+--='≤≤--='' 边界条件：0|011==x w ⇒ 01=D 0|22==l x w ⇒0 162414812244=++⋅-D l C ql ql 222132||l x l x w w ===⇒2211)2( )2(D l C D l C +=+ 222132||l x l x w w =='='⇒021==C C则：021==D D ，4213847ql C C -== 32111133113847 161)2(0 3847 481qlqlx w EI l x x ql qlx EIw -='≤≤-=3847)2(61 161)2( 3847)2(241 48133222222342322ql l x q qlx w EI l x l x ql l x q qlx EIw ---='≤≤---= AF BF1xEI ql w x A 3847|3011-='==θ EI ql w l x B 1283|322='==θ EIql l ql l ql EI w w C 3845)]2(3847 )2(481[13331-=-==7.3 用叠加法求下列各梁的指定位移。

材料力学(金忠谋)第六版答案第07章(总23页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除244习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI 为常量。

7－1（a ） 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ；'0y =代入上面方程可求得：C=D=0201M 2EJ y x ∴= '01=M EJy x θ= 01=M EJ B l θ 201=M 2EJB y l （b ）222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+- 3'2211EJ 226qx y ql x qlx C =-+-+ 422311EJ 4624qx y ql x qlx Cx D =-+-++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=02454223111()EJ 4624qx y ql x qlx ∴=-+- '2231111=(-)EJ 226y ql x qlx qx θ=+- 3-1=6EJ B ql θ 4-1=8EJB y ql （c ）()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l x q x q lq l x M x q x l x l x l q y l x lq y l x C lq y l x Cx D l-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++ 边界条件：0x = 时 0y = ；'0y = 代入上面方程可求得：4024q l C l -= 50120q l D l= ()455000232230120EJ 24EJ 120EJ (10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =- (d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D =-=-=-+=-++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=024623'232321112611253262B C C B y Pax Px EJ y Pax Px EJ Pa Pa Pa y y a a EJ EJ EJ Pa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==- ⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qax a y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=0()()()22118492024EJ 12EJqax qax y a x a x x a ∴=--=--≤≤ ''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++ 边界条件：x a = 时 12y y = ；12θθ=代入上面方程可求得：2296a C = 4224qa D =- ()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤247 43412476B B qa y EJ qa EJθ=-=- (f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件：x a = 时 12y y = ； ''''12y y =3296a C =- 4224a D =- 437124136B B qa y EJ qa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程，端截面转角θA 和θB ，跨度中点的挠度和最大挠度，梁的抗弯刚度EI 为常量。

[ ]
[]
0.5 x 0.4125
M(kN.m)
7
习题 7－10 图
解：画弯矩图如图所示： 对于梁：
M max = 0.5q M 0.5q σ max = max ≤ [σ ] , ≤ [σ ] W W [σ ]W = 160 ×106 × 49 ×10−6 = 15.68 ×103 N/m=15.68kN/m q≤ 0.5 0.5
A
B
W
a + Δa
W + ΔW
B
A
a图
b图
整理后得
Δa =
ΔW (l − a ) (W + ΔW )
此即为相邻跳水者跳水时，可动点 B的调节距离 Δa 与他们体重间的关系。 7－ 14 利用弯曲内力的知识，说明为何将标准双杠的尺寸设计成 a=l/4。
9
习题 7－14 图
解：双杠使用时，可视为外伸梁。 其使用时受力点应考虑两种引起最大弯矩的情况。如图a、b所示。
[ ]＋
[σ ]－ ＝120 MPa。试校核梁的强度是否安全。
6
30 x 10 M(kN.m) C 截面
+ = σ max － σ max
40
习题 7－9 图
30 ×103 N ⋅ m × 96.4 ×10−3 m = 28.35 × 106 Pa=28.35 MPa 1.02 ×108 ×10−12 m 4 30 ×103 N ⋅ m ×153.6 ×10−3 m = = 45.17 ×106 Pa=45.17 MPa 1.02 ×108 × 10−12 m 4 40 ×103 N ⋅ m ×153.6 ×10−3 m = 60.24 ×106 Pa=60.24 MPa> [σ ] 8 −12 4 1.02 ×10 × 10 m 40 ×103 N ⋅ m × 96.4 × 10−3 m = = 37.8 × 106 Pa=37.8 MPa 8 −12 4 1.02 × 10 × 10 m

答
案
网
τ 22.5°
ww
b 解 σ 22.5° =
− 30 + 10 − 30 − 10 cos 45° − 20 sin 45° = −38.3 MPa + 2 2 − 30 − 10 = sin 45° + 20 cos 45° = 0 2
w.
103
kh
da
w.
co
τ 45°
30 + 10 30 − 10 + cos 90° − (− 20 )sin 90° = 40 MPa 2 2 30 − 10 = sin 90° + (− 20 )cos 90° = 10 MPa 2
即
3 ， θ = 36.87° ， α = 90° − θ = 53.13° 4 σ α = 0 ， τ α = 0 ， τ max = 35 MPa σ +σ y σ x −σ y σα = x + cos 2α − τ xy sin 2α = 0 2 2 σ −σ y τα = x sin 2α + τ xy cos 2α = 0 2
代入式（b）得
σ 60° =
后
σ x + 40 σ x − 40
a 解 σ 45° =
课
c 解 σ −60 =
τ −60°
后
10 − 20 10 − (− 20 ) + cos(− 120°) − 15 sin (− 120°) = 0.490 MPa 2 2 10 − (− 20 ) = sin (− 120°) + 15 cos(− 120°) = 20.5 MPa 2
即
w. da
⎛σ x −σ y ⎞ 2 ⎟ τ max = ⎜ ⎜ ⎟ + τ xy = 35 2 ⎝ ⎠ σ x +σ y σ x −σ y + × (− 0.28) − τ xy × 0.96 = 0 2 2 σ x −σ y × 0.96 + τ xy × (− 0.28) = 0 2 2 ⎛σ x −σ y ⎞ 2 ⎜ ⎟ + τ xy = 1 225 ⎜ ⎟ 2 ⎠ ⎝

∑F
及
n
= 0， σ α dA = 0
∑F
分别得到
t
= 0， τ α dA = 0
σ α = 0，τ α = 0
由于方位角 α 是任取的，这就证明了 A 点处各截面上的正应力与切应力均为零。 顺便指出，本题用图解法来证更为方便，依据 A 点上方两个自由表面上的已知应力（零 应力）画应力图，该应力圆为坐标原点处的一个点圆。至此，原命题得证。
由此可知，主应力各为
σ1 = 60.0MPa, σ 2 = σ 3 = 0
5
σ1 的方位角为
α0 = 0o
对于应力图(b),其正应力和切应力分别为
σB = τB =
| M | | y B | 12 × 20 × 10 3 × 0.050 N = = 3.00 × 10 7 Pa = 30.0MPa 3 2 Iz 0.050 × 0.200 m Fs S z (ω) 12 × 20 × 10 3 × 0.050 × 0.050 × 0.075 N = = 2.25 × 10 6 Pa = 2.25MPa 3 2 I zb 0.050 × 0.200 × 0.050m
σα = (
− 30 + 10 − 30 − 10 + cos45 o − 20sin45 o )MPa = −38.3MPa 2 2 − 30 − 10 τα = ( sin45 o + 20cos45 o )MPa = 0 2
(c)解：由题图所示应力状态可知，
σ x = 10MPa，σ y = −20MPa，τ x = 15MPa，α = −60 o
7-7
已知某点 A 处截面 AB 与 AC 的应力如图所示（应力单位为 MPa） ，试用图解法

解：左支座为A，右支座为B，左集中力作用点为C，右集中力作用点为D。
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。

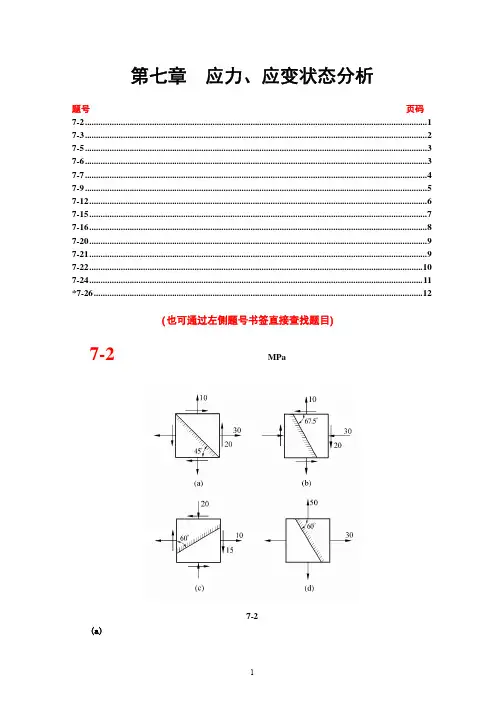
7-2. 在图示各单元体中，试用解析法和应力圆求斜面ab 上的应力。

应力单位为MPa 。

解：（a ）（1）应力分量oxyyxMPa MPa 30 0 70 70==-==ατσσ（2）用解析法求斜截面上的应力MPaMPaxyyxxyyxyx6.6060sin 270702cos 2sin 23560cos 27070270702sin 2cos 22=︒+=+-==︒++-=--++=ατασστατασσσσσαα（3）应力圆（b ）（1）应力分量oxyyxMPa MPa 30 0 70 70====ατσσ（2）用解析法求斜截面上的应力a)c)d)b)σ2cos 2sin 270270702sin 2cos 22=+-==+=--++=ατασστατασσσσσααxyxxyxyxMPa（3）应力圆：为一点圆（c ）（1）应力分量oxyyxMPa MPa 60 0 50 100====ατσσ（2）用解析法求斜截面上的应力MPaMPaxyxxyxyx7.21120sin 2501002cos 2sin 25.62120cos 2501002501002sin 2cos 22=︒-=+-==︒-++=--++=ατασστατασσσσσαα（3）应力圆σσ（d ）（1）应力分量oxyyxMPa MPa 150 0 100 50===-=ατσσ（2）用解析法求斜截面上的应力MPaMPaxyx xyxyx65300sin 2100502cos 2sin 25.12300cos 2100502100502sin 2cos 22=︒--=+-=-=︒--++-=--++=ατασστατασσσσσαα（3）应力圆7-3. 已知应力状态如图所示，图中的应力单位为MPa 。

试用解析法和应力圆求：（1）主应力大小，主平面位置；（2）在单元体上给出主平面位置及主应力方向；（3）最大剪应力。

解：（e ）（1）应力分量MPa MPa xyyx20 80 0=-==τσσ（2）求主平面位置和主应力大小20e)f)σoooyx xytg 7.7690 3.135.0220=+-=∴-=--=αασσταMPaMPa MPaMPa xyxyx7.84 0 7.47.847.420)280(280)2(23212222minmax-===∴⎩⎨⎧-=+±-=+-±+=⎩⎨⎧σσστσσσσσσ（3）主平面位置及主应力方向（4）最大剪应力MPa 7.4427.847.4231max=+=-=σστ（5）应力圆（f ）（1）应力分量MPa MPa MPa xyyx20 30 20==-=τσσ（2）求主平面位置和主应力大小ooo yxxytg 3.10990 3.198.0220=+=∴=--=αασστα1σMPaMPa MPaMPaxyxyx27 0 37273720)23020(23020)2(23212222minmax-===∴⎩⎨⎧-=+--±+-=+-±+=⎩⎨⎧σσστσσσσσσ （3）主平面位置及主应力方向（4）最大剪应力MPa 3222737231max=+=-=σστ（5）应力圆7-10. 薄壁圆筒的扭转-拉伸示意图如图所示。

题目二
说明杆件在拉伸或压缩时，其 应力与应变的关系。
题目三
一矩形截面梁，长度为L，截面 积为A，弹性模量为E，泊松比 为v，求梁的临界截面转角。
题目四
一圆截面杆，直径为D，弹性模 量为E，泊松比为v，求杆的临 界截面转角。
答案
第一季度
第二季度
第三季度
第四季度
答案一
材料力学的研究对象是 固体，特别是金属和复 合材料等工程材料。其 基本假设包括连续性假 设、均匀性假设、各向 同性假设和小变形假设 。
解析四
圆截面杆的临界截面转角是指杆在受到扭矩作用 时发生弯曲变形的角度。通过弹性力学和材料力 学的知识，我们可以计算出这个角度的值。其中 ，D表示杆的直径，E表示杆的弹性模量，v表示 杆的泊松比。
03
习题三答案及解析
题目
• 题目：一矩形截面简支梁，其长度为L，截面高为h，宽度为b，且h/b=2，梁上作用的均布载荷q=100N/m，试求梁上最大 弯矩值Mmax。
解释了材料力学的基本假设，包括连续性假设、 均匀性假设、各向同性假设和线性弹性假设。这 些假设是材料力学中常用的基本概念，对于简化 复杂的实际问题、建立数学模型以及进行实验研 究具有重要的意义。
题目二解析
强调了材料力学在工程实践中的重要性，说明了 它为各种工程结构的设计、制造、使用和维护提 供了理论基础和实验依据，能够保证工程结构的 可靠性和安全性。这表明了材料力学在工程实践 中的实际应用价值。
题目四解析
解释了材料力学中的应力和应变概念，说明了应 力表示单位面积上的内力，应变表示材料在受力 过程中发生的变形程度。这些概念是材料力学中 的基本概念，对于理解和分析材料的力学行为具 有重要的意义。
THANK YOU

第七章应力、应变状态分析7-1 已知应力状态如图所示（应力单位为），试用解析法计算图中指定截面的正应力与切应力。

解：与截面的应力分别为：；；；MPa7-2已知应力状态如图所示（应力单位为），试用解析法计算图中指定截面的正应力与切应力。

解：与截面的应力分别为：；；；7-6已知应力状态如图所示（应力单位为），试用图解法计算图中指定截面的正应力与切应力。

解：如图，得：指定截面的正应力切应力7-7 已知某点A处截面AB与AC的应力如图所示（应力单位为），试用图解法求主应力的大小及所在截面的方位。

解：由图，根据比例尺，可以得到，，7-8已知应力状态如图所示，试画三向应力圆，并求主应力、最大正应力与最大切应力。

解：对于图示应力状态，是主应力状态，其它两个主应力由、、确定。

在平面内，由坐标(,)与(,)分别确定和点，以为直径画圆与轴相交于和。

再以及为直径作圆，即得三向应力圆。

由上面的作图可知，主应力为，，，7-9已知应力状态如图所示（应力单位为），试求主应力的大小。

解：与截面的应力分别为：；；；在截面上没有切应力，所以是主应力之一。

；；；7-11已知构件表面某点处的正应变，，切应变，试求该表面处方位的正应变与最大应变及其所在方位。

解：得：7-12图示矩形截面杆，承受轴向载荷F作用，试计算线段AB的正应变。

设截面尺寸b和h与材料的弹性常数E和μ均为已知。

解：，，，AB的正应变为7-13在构件表面某点O处，沿，与方位，粘贴三个应变片，测得该三方位的正应变分别为，与，该表面处于平面应力状态，试求该点处的应力，与。

已知材料的弹性模量，泊松比解：显然，，并令，于是得切应变：第八章复杂应力状态强度8-1 圆截面轴的危险面上受有弯矩Ｍy、扭矩Ｍx和轴力ＦN x作用，关于危险点的应力状态有下列四种。

试判断哪一种是正确的。

请选择正确答案。

（图中微元上平行于纸平面的面对应着轴的横截面）答：B8-2图示钢质拐轴，承受集中载荷F作用。

作业参考答案（7-10章）7-１ (a )已知：045201030=-===ατσσMPa MPaMPaxy y xMPa MPa xy yx xy yx yx 1045220452210302224045220452210302103022224545=︒⨯-︒⨯-=+-==︒⨯+︒⨯-++=--++=cos sin cos sin sin cos sin cos ατασστατασσσσσ (b )已知：05.67203010-=-=-==ατσσMPaMPa MPaxy y x567220567223010222343856722056722(-30)102(-30)102222=︒⨯--+︒⨯-+=+-=-=︒⨯-+︒⨯--++=--++=).cos()().sin(cos sin .).sin().cos(sin cos ατασστατασσσσσααxy y x xy yx y x MPa(d )已知：012003050-====ατσσxy y x MPaMPaMPa MPa xy yx xy yx yx 668240230502223524023050230502222..)sin(cos sin )cos(sin cos -=︒--=+-==︒--++=--++=ατασστατασσσσσαα7-2 (a )已知：MPa MPaMPaxy y x 202040===τσσ︒-=︒︒-=-=-⨯-=--====⎩⎨⎧=+⎪⎭⎫ ⎝⎛-±+=+⎪⎪⎭⎫ ⎝⎛-±+=⎩⎨⎧3587316116463222040202220647365264736522022040220402200003212222....tan ....min max αασστασσστσσσσσσyx xyxy y x y x xMPa MPa MPa MPa(a )7-3(a )解：MPaMPa MPaMPaMPa 6527060260703060311321=+=-===-===σστσσσσσmax max(b )解：给定应力状态中有一个主应力是已知的，即σz =30MPa 。

第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

（图 1）
（图 2）
3．有 A、B、C 三种材料，其拉伸应力—应变实验曲线如图 3 所示，曲线( B )材料
的弹性模量 E 大，曲线( A )材料的强度高，曲线( C )材料的塑性好。
4．材料经过冷作硬化后，其( D )。
A．弹性模量提高，塑性降低
B． 弹性模量降低，塑性提高
C．比例极限提AB 梁的中点
D 任意点
14. 轴向拉伸杆，正应力最大的截面和剪应力最大的截面 ( A )
A 分别是横截面、450 斜截面
B 都是横截面
C 分别是 450 斜截面、横截面
D 都是 450 斜截面
15. 设轴向拉伸杆横截面上的正应力为σ，则 450 斜截面上的正应力和剪应力( D )。
A σ＝Eε＝300MPa
B σ＞300MPa
C 200MPa＜σ＜300Mpa
D σ＜200MPa
21．图 9 分别为同一木榫接头从两个不同角度视图，则（ B ）。
A. 剪切面面积为 ab,挤压面面积为 ch； B. 剪切面面积为 bh,挤压面面积为 bc；
C. 剪切面面积为 ch,挤压面面积为 bc； D. 剪切面面积为 bh,挤压面面积为 ch。
F
p
.D
.
.
.
.
...
解：设每个螺栓受力为 F，由平衡方程得
根据强度条件，有 ［σ］≥
故螺栓的内径取为 24mm。 4．图示一个三角架，在节点 B 受铅垂荷载 F 作用，其中钢拉杆 AB 长 l1=2m，截面面
积 A1=600mm2，许用应力 [ ]1 160MPa ，木压杆 BC 的截面面积 A2=1000mm2，许 用应力 [ ]2 7MPa 。试确定许用荷载[F]。