材料力学作业参考题解_扭转.

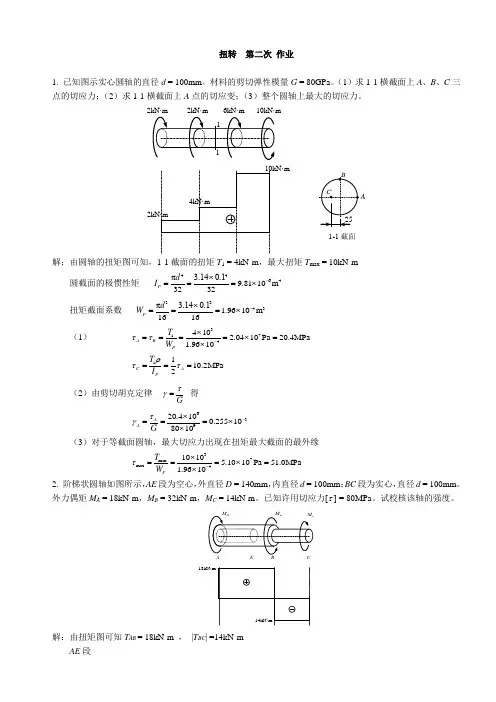
扭转 第二次 作业1. 已知图示实心圆轴的直径d = 100mm 。

材料的剪切弹性模量G = 80GPa 。

（1）求1-1横截面上A 、B 、C 三点的切应力；（2）求1-1横截面上A 点的切应变；（3）整个圆轴上最大的切应力。

2kN·m6kN·m10kN·m2kN·m1-1截面2kN·m4kN·m10kN·m解：由圆轴的扭矩图可知，1-1截面的扭矩T 1 = 4kN·m ，最大扭矩T max = 10kN·m圆截面的极惯性矩 4464π 3.140.19.8110m 3232P d I -⨯===⨯扭矩截面系数 3343π 3.140.1 1.9610m 1616P d W -⨯===⨯（1） 3714410 2.0410Pa 20.4MPa 1.9610A B P T W ττ-⨯====⨯=⨯ 1110.2MPa 2C A P T I ρττ=== （2）由剪切胡克定律 Gτγ=得63920.4100.255108010AA G τγ-⨯===⨯⨯ （3）对于等截面圆轴，最大切应力出现在扭矩最大截面的最外缘37max max41010 5.1010Pa 51.0MPa 1.9610P T W τ-⨯===⨯=⨯ 2. 阶梯状圆轴如图所示，AE 段为空心，外直径D = 140mm ，内直径d = 100mm ；BC 段为实心，直径d = 100mm 。

外力偶矩M A = 18kN·m ，M B = 32kN·m ，M C = 14kN·m 。

已知许用切应力[τ ] = 80MPa 。

试校核该轴的强度。

18kN·m14kN·m解：由扭矩图可知T AB = 18kN·m ， |T BC | =14kN·mAE 段()4334431π 3.140.1410011 3.9810m 1616140P D W α-⎛⎫⨯⎛⎫=-=-=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭[]36max41181045.210Pa 45.2MPa<3.9810AB P T W ττ-⨯===⨯=⨯ BC 段33432π 3.140.1 1.9610m 1616P d W -⨯===⨯ []36max 42141071.410Pa 71.4MPa<1.9610BC P T W ττ-⨯===⨯=⨯ 故，该轴安全。

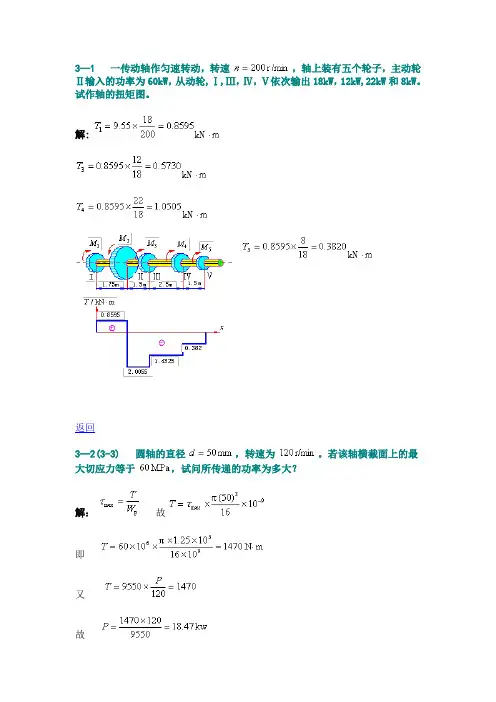
3—1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮,Ⅰ,Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

试作轴的扭矩图。

解:kNkNkNkN返回3—2(3-3)圆轴的直径，转速为。

若该轴横截面上的最大切应力等于，试问所传递的功率为多大？解：故即又故返回3—3（3—5）实心圆轴的直径mm，长m，其两端所受外力偶矩，材料的切变模量。

试求:（1)最大切应力及两端截面间的相对扭转角；（2)图示截面上A，B，C三点处切应力的数值及方向；（3）C点处的切应变。

解：=返回3-4(3—6)图示一等直圆杆，已知，，，。

试求:（1）最大切应力；（2）截面A相对于截面C的扭转角。

解：(1）由已知得扭矩图（a）(2)返回3-5(3—12)长度相等的两根受扭圆轴，一为空心圆轴，一为实心圆轴,两者材料相同,受力情况也一样。

实心轴直径为d;空心轴外径为D，内径为，且。

试求当空心轴与实心轴的最大切应力均达到材料的许用切应力），扭矩T相等时的重量比和刚度比。

解：重量比=因为即故故刚度比==返回3—6(3-15）图示等直圆杆，已知外力偶矩,，许用切应力，许可单位长度扭转角，切变模量。

试确定该轴的直径d。

解:扭矩图如图（a)(1)考虑强度，最大扭矩在BC段,且(1）(2）考虑变形（2）比较式（1）、(2），取返回3-7(3—16) 阶梯形圆杆,AE段为空心,外径D=140mm，内径d=100mm；BC段为实心，直径d=100mm。

外力偶矩，，。

已知：，,。

试校核该轴的强度和刚度。

解:扭矩图如图（a)（1)强度=，BC段强度基本满足=故强度满足。

（2）刚度BC段：BC段刚度基本满足.AE段：AE段刚度满足，显然EB段刚度也满足.返回3—8(3-17）习题3—1中所示的轴,材料为钢,其许用切应力，切变模量，许可单位长度扭转角。

试按强度及刚度条件选择圆轴的直径。

解:由3—1题得：故选用.返回3-9(3-18）一直径为d的实心圆杆如图，在承受扭转力偶矩后，测得圆杆表面与纵向线成方向上的线应变为。

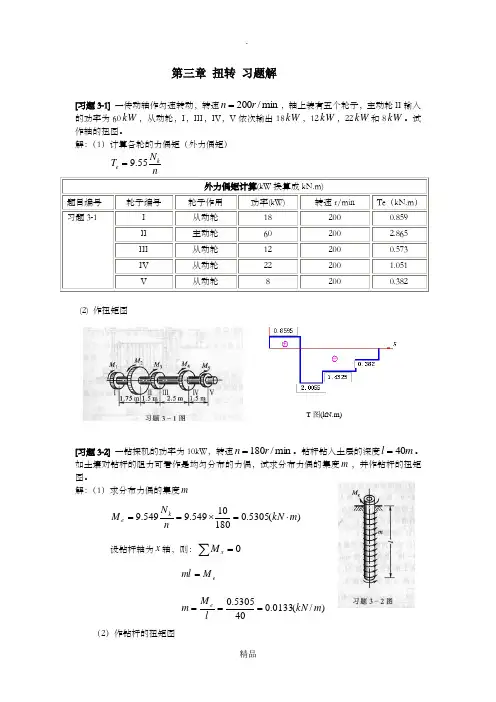
第三章扭转 习题解[习题3-1] 一传动轴作匀速转动，转速min /200r n =，轴上装有五个轮子，主动轮II 输入的功率为60kW ，从动轮，I ，III ，IV ，V 依次输出18kW ，12kW ，22kW 和8kW 。

试作轴的扭图。

解：（1）计算各轮的力偶矩（外力偶矩） nN T ke 55.9= 外力偶矩计算(kW 换算成kN.m)题目编号 轮子编号轮子作用 功率(kW) 转速r/minTe （kN.m ） 习题3-1I 从动轮 18 200 0.859 II 主动轮 60 200 2.865 III 从动轮 12 200 0.573 IV 从动轮 22 200 1.051 V从动轮82000.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ，转速min /180r n =。

钻杆钻入土层的深度m l 40=。

如土壤对钻杆的阻力可看作是均匀分布的力偶，试求分布力偶的集度m ，并作钻杆的扭矩图。

解：（1）求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴，则：0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===（2）作钻杆的扭矩图T 图(kN.m)x x lM mx x T e0133.0)(-=-=-=。

]40,0[∈x 0)0(=T ； )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。

[习题3-3] 圆轴的直径mm d 50=，转速为120r/min 。

若该轴横截面上的最大切应力等于60MPa ，试问所传递的功率为多大？ 解：（1）计算圆形截面的抗扭截面模量：)(245445014159.3161161333mm d W p =⨯⨯==π （2）计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=（3）计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=，内径mm d 50=。

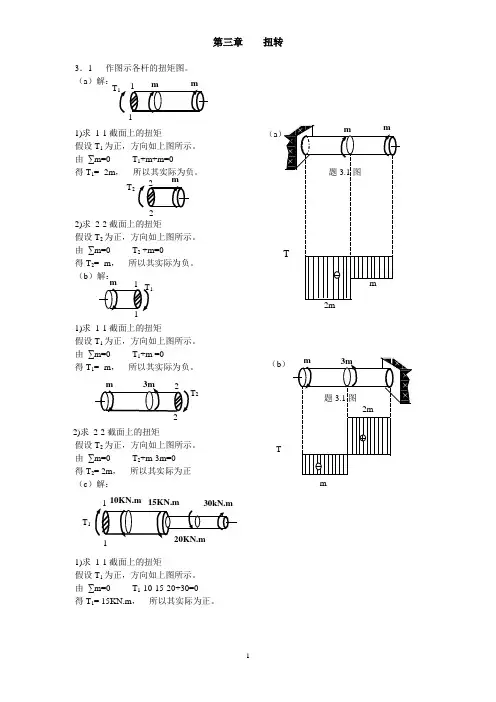
第三章 扭转3．1 作图示各杆的扭矩图。

（a ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1+m+m=0得T 1= -2m ， 所以其实际为负。

2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2 +m=0得T 2= -m ， 所以其实际为负。

（b ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1+m =0得T 1= -m ， 所以其实际为负。

2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2+m-3m=0 得T 2= 2m ， 所以其实际为正 （c ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m ， 所以其实际为正。

T 1T 2（a2（b ）mTT 12)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m ， 所以其实际为正。

3)求 3-3截面上的扭矩 假设T 3为正，方向如上图所示。

由 ∑m=0 T 3-20+30=0得T 3= -10KN.m ， 所以其实际为负。

4)求 4-4截面上的扭矩假设T 4为正，方向如上图所示。

由 ∑m=0 T 4 +30=0得T 4= -30KN.m ， 所以其实际为负。

3.2 T 为圆杆横截面上的扭矩，试画出截面上与T 对应的剪应力分布图。

解：3.5 D=50mm 直径的圆轴，受到扭矩T=2.15KN .m 的作用。

试求在距离轴心10mm 处的剪应力，并求轴横截面上的最大剪应力。

T 230kN.m T 3T 4（题3.2图（a ） （b ）解：求距离轴心10mm 处的剪应力， 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ，d 2=70mm ，轴上装有三个皮带轮，如图所示。

第三章 扭 转一、判断题1．圆杆受扭时，杆内各点均处于纯剪切状态。

（ ） 2．非圆截面杆不能应用圆杆扭转切应力公式，是因为非圆截面杆扭转时“平面假设”不能成立。

（ ） 3．当剪应力超过材料的剪切比例极限时，剪应力互等定律亦成立。

（ ） 4．一点处两个相交面上的剪应力大小相等，方向指向（或背离）该两个面的交线。

（ ） 5．直径和长度相同，材料不同的两根轴，受相同的扭转力偶矩作用，它们的最大剪应力和最大扭转角都相同。

6. 杆件受扭时，横截面上最大切应力发生在距截面形心最远处。

（ ）7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。

（ ）8. 圆杆扭转变形实质上是剪切变形。

（ ）9. 横截面的角点处的切应力必为零。

（ ） 1.√ 2.√ 3.√ 4.× 5.× 6.×（非圆截面） 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的（ ）。

A ．大小相等，正负号相同；B ．大小不等，正负号相同； C ．大小不等，正负号不同；D ．大小相等，正负号不同。

2. 直径为D 的实心圆轴，两端受扭转力矩作用。

轴内最大剪应力τ，若轴的直径改为D/2，则轴内的最大剪应力变为（ ）。

A ．2τ； B ．τ； C ． 8τ； D ．16τ。

3. 阶梯圆轴的最大切应力发生在（ ）。

A ．扭矩最大的截面；B ．直径最小的截面；C ．单位长度扭转角最大的截面；D ．不能确定。

4.空心圆轴的外径为D ，内径为d,α=d/D 。

其抗扭截面系数为（ ）。

A ．()απ-=1163D W P ；B 。

()23116απ-=D W P ；C 。

()33116απ-=D W PD ．()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于（ ）杆件。

A ．任意截面； B ．任意实心截面；C ．任意材料的圆截面； D ．线弹性材料的圆面。

扭 转1. 一直径为1D 的实心轴，另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴，若两轴横截面上的扭矩和最大切应力均分别相等，则两轴的横截面面积之比12/A A 有四种答案：(A) 21α-； (B)(C)； (D)。

2. 圆轴扭转时满足平衡条件，但切应力超过比例极限，有下述四种结论： (A) (B) (C) (D) 切应力互等定理： 成立 不成立 不成立 成立 剪切胡克定律： 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴，当两端承受扭转力偶时，若横截面上的最大切应力为τ，则内圆周处的切应力有四种答案：(A) τ ； (B) ατ； (C) 3(1)ατ-； (D) 4(1)ατ-。

4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。

扭转时，表面的纵向线倾斜了γ角，在小变形情况下，此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案：7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料， 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。

10. 矩形截面杆扭转变形的主要特征是 。

1-10题答案：1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩；4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ，扭转加载到整个截面全部屈服，将扭矩卸掉所产生的残余应力如图所示，试证明图示残余应力所构成的扭矩为零。

证：截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。

12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示，式中C ，m 为由实验测定的已知常数，试证明该轴的扭转切应力计算公式为：1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证：几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。

电气工程师-公共基础-材料力学-扭转[单选题]1.已知实心圆轴按强度条件可承担的最大扭矩为T，若改变该轴的直径，使其横截面积增加1倍。

则可承担的最大扭矩为()。

[2019年真（江南博哥）题]A.B.2TC.D.4T正确答案：C参考解析：扭转剪应力公式为：。

式中，Wp为抗扭截面系数，且。

当横截面面积增加一倍时，直径变为原来的倍。

根据扭转剪应力公式，当最大剪应力不变时，直径变为原来的倍时，可承受的最大扭矩为。

[单选题]2.圆轴直径为d，剪切弹性模量为G，在外力作用下发生扭转变形，现测得单位长度扭转角为θ，圆轴的最大切应力是()。

[2013、2010年真题]A.τ＝（16θG）/（πd3）B.τ＝（θGπd3）/16C.τ＝θGdD.τ＝θGd/2正确答案：D参考解析：由公式θ＝T/（GIp）得：T＝θGIp。

其中，Ip＝（d/2）·Wp。

则最大切应力τ＝T/Wp＝GθIp/Wp＝θGd/2。

[单选题]3.在一套传动系统中，有多根圆轴，假设所有圆轴传递的功率相同，转速不同。

该系统的圆轴转速与其扭矩的关系是()。

[2016、2014年真题]A.转速快的轴扭矩大B.转速慢的轴扭矩大C.全部轴的扭矩相同D.无法确定正确答案：B参考解析：根据公式T＝9550P/n可知，在功率相同的情况下转速慢的轴扭矩大。

式中，T为扭矩（N·m）；P为功率（kW）；n为转速（r/min）；9550为常系数。

[单选题]4.图5-3-1所示两根圆轴，横截面面积相同，但分别为实心圆和空心圆。

在相同的扭矩T作用下，两轴最大切应力的关系是()。

[2013年真题]图5-3-1A.τa＜τbB.τa＝τbC.τa＞τbD.不能确定正确答案：C参考解析：设d1为实心圆直径，D2为空心圆截面外径，d2为空心圆截面内径，α2＝d2/D2。

由最大切应力公式τmax＝T/WP，由两轴截面面积相等得：πd12/4＝πD22（1－α22）/4，即：实心圆截面的抗扭截面系数WPa＝πd13/16；空心圆截面的WPb＝πD23（1－α24）/16，因此两轴的抗扭截面系数之比为：故τa＞τb。

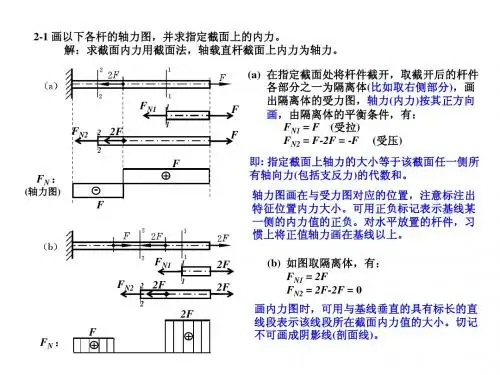
19-1 19-2 19-3 19-5 19-4、19-8 19-1019-1 绘制图示各杆的扭矩图。

参考答案略19-2 直径为D =5cm 的圆轴，受到扭矩n M =2.15kN ·m 的作用，试求在距离轴心1cm 处的剪应力，并求轴截面上的最大剪应力。

参考答案：由圆轴扭转横截面上任意一点剪应力计算公式可知，距轴心1cm 处的剪应力为MPa I M pn 353250101015.246=⨯⨯⨯==πρτρ截面上的最大剪应力：MPa W M tn 6.8716501015.236max =⨯⨯==πτ 19-3 已知作用在变截面钢轴上的外力偶矩1m =1.8kN ·m ，2m =1.2kN ·m 。

试求最大剪应力和最大相对转角。

材料的G =80GPa 。

参考答案：直径为75mm 段的扭矩为m KN m m T .3)(211-=+-=； 直径为50mm 段的扭矩为KNm m T 2.122-=-=。

最大剪应力计算：MPa W T t 2.3616751033611max 1=⨯⨯==πτ；MPa W T t 9.481650102.13622max 2=⨯⨯==πτ则最大剪应力MPa 9.48max =τ最大相对转角计算：22.10212773.0102231.121005416.932501080500102.13275108075010333436436222111max 2max 1max ==⨯+⨯=⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=+=+=--rad rad rad GI lT GI l T P P ππϕϕϕ 19-4 已知圆轴的转速n =300r /min ，传递功率330.75kW ，材料的][τ=60MPa ，G =82GPa 。

要求在2m 长度内的相对扭转角不超过1º，试求该轴的直径。

参考答案：计算外力偶矩（即扭矩）：m N n N Me T ⋅=⨯===875.1052830075.33095509550按强度条件设计轴的直径：[]MPa d W T t601610875.1052833max =≤⨯==τπτ mm d 32.966010875.105281633=⨯⨯≥π按刚度条件设计轴的直径：118032108210210875.105281804333max ≤⨯⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=⨯=πππϕd GI Tl p 得 mm d 64.110108232180********.1052842333=⨯⨯⨯⨯⨯⨯⨯≥π故该轴的直径mm d 64.110≥19-5 图示一圆截面直径为80cm 的传动轴，上面作用的外力偶矩为1m =1000N ·m ，2m =600N ·m ，3m =200N ·m ，4m =200N ·m ，（1）试作出此轴的扭矩图，（2）试计算各段轴内的最大剪应力及此轴的总扭转角（已知材料的剪切弹性模量G =79GPa ）；（3）若将外力偶矩1m 和2m 的作用位置互换一下，问圆轴的直径是否可以减少？注意：此题传动轴直径应为80mm 。

-12-基本概念题一、选择题（如果题目有5个备选答案，选出 2〜5个正确答案，有 4个备选答案选出 一个正确答案。

）1. 图示传动轴，主动轮 A 的输入功率为 P A = 50 kW ，从动轮B ，C , D ，E 的输出功率 分另为 P B = 20 kW ，P C = 5 kW ，P D = 10 kW ，P E = 15 kW 。

则轴上最大扭矩 T 出现在max)。

A . BA 段B . AC 段C . CD 段D . DE 段题1图2.图示单元体的应力状态中属正确的纯剪切状态的是（ ）。

题2图3. 上题图示单元体的应力状态中属正确的是（4. 下列关于剪应力互等定理的论述中正确的是（ A. 剪应力互等定理是由平衡B. 剪应力互等定理仅适用于纯剪切的情况C. 剪应力互等定理适用于各种受力杆件D. 剪应力互等定理仅适用于弹性范围E. 剪应力互等定理与材料的性能无关5.图示受扭圆轴，其横截面上的剪应力分布图正确的是鼻i题5图6.实心圆轴，两端受扭转外力偶作用。

直径为D时，设轴内的最大剪应力为，若轴的直径改为D 2，其它条件不变，则轴内的最大剪应力变为（）。

A. 8 C. 167.受扭空心圆轴（d/D ）,在横截面积相等的条件下，下列承载能力最大的轴是( )°A. 0 （实心轴）B.0.5 C. 0.6 0.88. 扭转应力公式+的适用范围是（A.C.9. B .实心或空心圆截面直杆D .弹性变形各种等截面直杆矩形截面直杆直径为D的实心圆轴，最大的容许扭矩为T,若将轴的横截面积增加一倍，则其最大容许扭矩为（E.弹性非弹性范围A. -2TB. 2TC. 2 2TD. 4T10.材料相同的两根圆轴，一根为实心，直径为D1；另一根为空心，内径为d2，外径亠d2为D2 £°若两轴横截面上的扭矩T,和最大剪应力max均相同，则两轴外径之比旦D2A. 1B. 1C. (1 3)13 4.13D . (1 )11.阶梯圆轴及其受力如图所示, 其中AB段的最大剪应力max1 与BC段的最大剪应力max2的关系是（)°A Rmax1 max 2 max1 3max22Cmax1 max 2D. max138 max2-13--14-题12图题13图12.在图示的圆轴中，AB 段的相对扭转角1和 BC段的相对扭转角2的关系:()。

材料力学第三章答案【篇一：材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴，关于如下结论：①最大剪应力只出现在横截面上；②在横截面上和包含杆件的纵向截面上均无正应力；③圆轴内最大拉应力的值和最大剪应力的值相等。

现有四种答案，正确的是（ a ）a ②③对 b①③对 c①②对d 全对 7.扭转切应力公式?mnp?i?适用于（ d）杆件。

pa 任意杆件；b 任意实心杆件；c 任意材料的圆截面；d 线弹性材料的圆截面。

9.若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ d a 2倍； b 4倍； c 8倍； d 16倍。

三、计算题1.试用截面法求出图示圆轴各段内的扭矩t，并作扭矩图2.图示圆轴上作用有四个外力偶矩 me1 =1kn/m, me2 =0.6kn/m,）me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图；⑵若 me1与me2的作用位置互换，扭矩图有何变化？(1)(2)解： me1与me2的作用位置互换后，最大扭矩变小。

3.如图所示的空心圆轴，外径d=100㎜，内径d=80㎜，m=6kn/m,m=4kn/m.请绘出轴的扭矩图，并求出最大剪应力解：扭矩图如上，则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜，l=500tr4?103?50?103ip5.8?104．图示圆形截面轴的抗扭刚度为g ip，每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。

ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二：《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动，转速n?200r/min，轴上装有五个轮子，主动轮ii输入的功率为60kw，从动轮，i，iii，iv，v依次输出18kw，12kw，22kw和8kw。

扭 转1. 一直径为1D 的实心轴，另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴，若两轴横截面上的扭矩和最大切应力均分别相等，则两轴的横截面面积之比12/A A 有四种答案：(A) 21α-； (B)(C)； (D)。

2. 圆轴扭转时满足平衡条件，但切应力超过比例极限，有下述四种结论： (A) (B) (C) (D) 切应力互等定理： 成立 不成立 不成立 成立 剪切胡克定律： 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴，当两端承受扭转力偶时，若横截面上的最大切应力为τ，则内圆周处的切应力有四种答案：(A) τ ； (B) ατ； (C) 3(1)ατ-； (D) 4(1)ατ-。

4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。

扭转时，表面的纵向线倾斜了γ角，在小变形情况下，此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案：料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D 重量比21W W 9. 10. 矩形截面杆扭转变形的主要特征是 。

1-10题答案：1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩；4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ，扭转加载到整个截面全部屈服，将扭矩卸掉所产生的残余应力如图所示，试证明图示残余应力所构成的扭矩为零。

证：截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。

12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示，式中C ，m 式为：证：几何方面 d d xρϕγρ=物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。