利用bode图求传递函数例题
- 格式:doc
- 大小:250.00 KB
- 文档页数:2
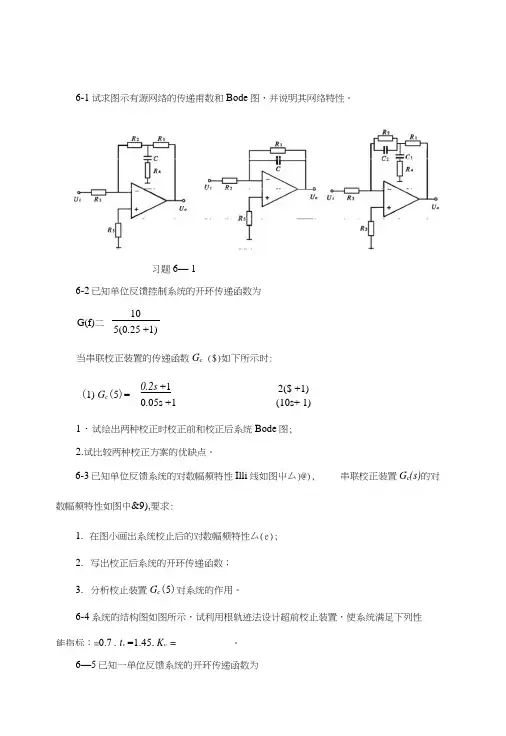
6-1试求图示有源网络的传递甫数和Bode 图,并说明其网络特性。
6-2已知单位反馈控制系统的开环传递函数为G(f)二 105(0.25 +1)当串联校正装置的传递函数G c ($)如下所示时:(1) G c (5)= 0.2s +10.05s +1 2($ +1) (10s+ 1)1・试绘出两种校正时校正前和校正后系统Bode 图;2.试比较两种校正方案的优缺点。
6-3已知单位反馈系统的对数幅频特性Illi 线如图屮厶)@),串联校正装置G c (s)的对数幅频特性如图中&9),要求: 1. 在图小画出系统校止后的对数幅频特性厶(e);2. 写出校正后系统的开环传递函数;3. 分析校止装置G c (5)对系统的作用。
6-4系统的结构图如图所示,试利用根轨迹法设计超前校止装置,使系统满足下列性 能指标:=0.7 , t s =1.45, K v = 。
6—5已知一单位反馈系统的开环传递函数为习题6— 1图试设计一•校正装置,使系统的相角裕量厂> 45° ,剪切频率0. > 50$ j 06-6单位反馈系统的开环传递函数为设计一串联滞后校正装置,使系统相角裕量/ > 40° ,并保持原有的开环增益。
6-7设单位反馈系统的开环传递函数为G(s)= --------------- ------------ 5(0.15 + 1)(0.255 + 1)试设计--校正装置,使系统满足下列性能指标,速度误差系数K,, 相角裕量 / > 40° ,剪切频率 > 0.5s~} o6-8单位反馈系统的开环传递函数为若耍求校正后系统的谐振峰值=1.4,谐振频率> lor 1,试确定校正装置的形 式与参数。
6-9单位反馈系统的结构如图所示,现用速度反馈来校正系统,校正后系统具有临界 G(s) =2005(0.15 + 1) G() =4 s(2s +1) G(s)=10 5(0.255 +1)(0.055 +1)习题6 —3图阻尼比< 试确定校正装置参数K,。
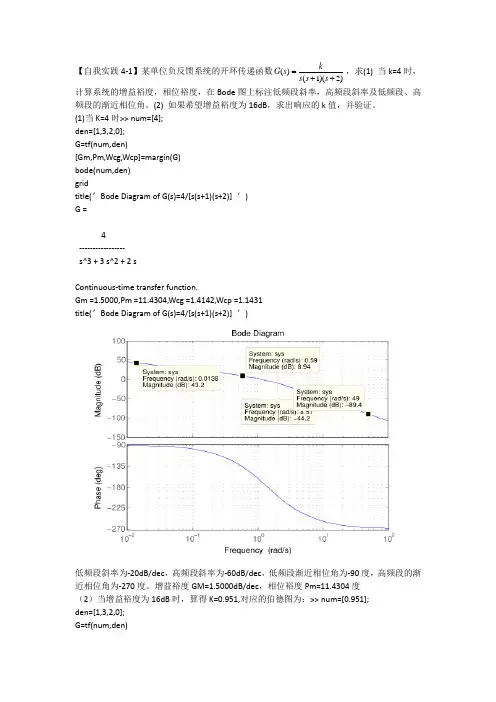
【自我实践4-1】某单位负反馈系统的开环传递函数()(1)(2)kG s s s s =++,求(1) 当k=4时,计算系统的增益裕度,相位裕度,在Bode 图上标注低频段斜率,高频段斜率及低频段、高频段的渐近相位角。
(2) 如果希望增益裕度为16dB ,求出响应的k 值,并验证。
(1)当K=4时>> num=[4]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G =4----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =1.5000,Pm =11.4304,Wcg =1.4142,Wcp =1.1431 title(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′)低频段斜率为-20dB/dec ,高频段斜率为-60dB/dec ,低频段渐近相位角为-90度,高频段的渐近相位角为-270度。
增益裕度GM=1.5000dB/dec ,相位裕度Pm=11.4304度 (2)当增益裕度为16dB 时,算得K=0.951,对应的伯德图为:>> num=[0.951]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G = 0.951 ----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =6.3091,Pm =54.7839,Wcg =1.4142,Wcp =0.4276 title(′Bode Diagram ′)【自我实践4-2】系统开环传递函数()(0.51)(0.11)kG s s s s =++,试分析系统的稳定性。

习 题 66-1 设控制系统的开环传递函数为:()()()s s s s G 1.015.0110++= 绘出系统的Bode 图并求出相角裕量和幅值裕量。
若采用传递函数为(1+0.23s)/(1+0.023s)的串联校正装置,试求校正后系统的幅值和相角裕度,并讨论校正后系统的性能有何改进。
6—2设控制系统的开环频率特性为()()()()ωωωωωj j j j H j G 25.01625.011++= ①绘出系统的Bode 图,并确定系统的相角裕度和幅值裕度以及系统的稳定性; ②如引入传递函数()()()0125.025.005.0++=s s s G c 的相位滞后校正装置,试绘出校正后系统的Bode 图,并确定校正后系统的相角裕度和幅值裕度。
6 3设单位反馈系统的开环传递函数为()()()8210++=s s s s G 设计一校正装置,使静态速度误差系数K v =80,并使闭环主导极点位于s=-2±j23。
6-4设单位反馈系统的开环传递函数为()()()93++=s s s K s G ①如果要求系统在单位阶跃输入作用下的超凋量σ =20%,试确定K 值;②根据所确定的K 值,求出系统在单位阶跃输入下的调节时间t s 。
,以及静态速度误差系数; ③设计一串联校正装置,使系统K v ≥20,σ≤25%,t s 减少两倍以上。
6 5 已知单位反馈系统开环传递函数为()()()12.011.0++=s s s K s G 设计校正网络,使K v ≥30,γ≥40º,ωn ≥2.5,K g ≥8dB 。
6-6 由实验测得单位反馈二阶系统的单位阶跃响应如图6-38所示.要求①绘制系统的方框图,并标出参数值;②系统单位阶跃响应的超调量σ =20%,峰值时间t p =0.5s ,设计适当的校正环节并画出校正后系统的方框图。
6-7设原系统的开环传递函数为()()()15.012.010++=s s s s G 要求校正后系统的相角裕度γ=65º。

自动控制理论第五章习题汇总填空题1、系统的频率响应与正弦输入信号之间的关系称为频率响应2、在正弦输入信号的作用下,系统输入的稳态分量称为频率响应简答题:5-2、什么是最小相位系统及非最小相位系统?最小相位系统的主要特点是什么?答在s平面上,开环零、极点均为负实部的系统称为最小相位系统;反之,开环零点或极点中具有正实部的系统称为非最小相位系统。
最小相位系统的主要特点是:相位滞后最小,并且幅频特性与相频特性有惟一的确定关系。
如果知道最小相位系统的幅频特性,可惟一地确定系统的开环传递函数。
5-3、什么是系统的频率响应?什么是幅频特性?什么是相频特性?什么是频率特性?答对于稳定的线性系统,当输入信号为正弦信号时,系统的稳态输出仍为同频率的正弦信号,只是幅值和相位发生了改变,如图5-3所示,称这种过程为系统的频率响应。
图5-3称为系统的幅频特性,它是频率的函数;称为系统的相频特性,它是频率的函数:称为系统的频率特性。
稳定系统的频率特性可通过实验的方法确定。
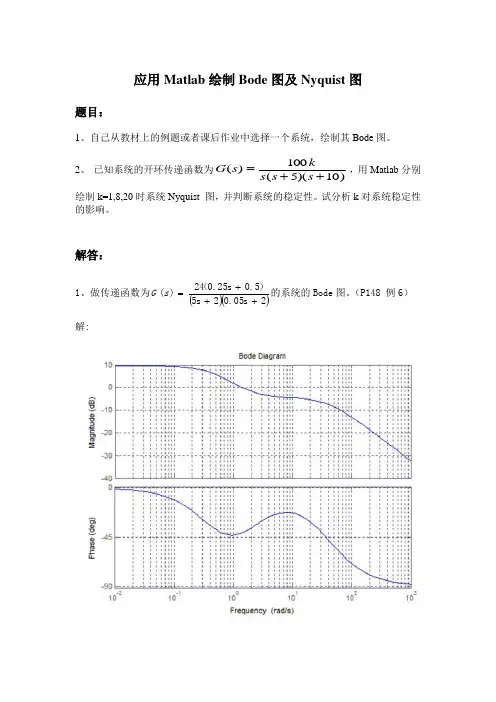
计算题5-1、设某控制系统的开环传递函数为)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图,并确定剪切频率c ω的值。
解:Bode 图如下所示剪切频率为s rad c /75.0=ω。
5-2、某系统的结构图和Nyquist 图如图(a)和(b)所示,图中2)1(1)(+=s s s G 23)1()(+=s s s H 试判断闭环系统稳定性,并决定闭环特征方程正实部根的个数。
解:由系统方框图求得内环传递函数为:ss s s s s s H s G s G +++++=+23452474)1()()(1)( 内环的特征方程:04742345=++++s s s s s由Routh 稳定判据:1:0310:16:44:171:01234s s s s s由此可知,本系统开环传函在S 平面的右半部无开环极点,即P=0。




2-1若i x 为输入位移,o x 为输出位移, 试列写出下图所示机械系统的微分方程式,并求出传递函数。
2-2下图所示系统中电压1U 和位移1x 为系统输入量,电压2U 和位移2x 为输出量,k 为弹簧弹性系数,f 为阻尼器的阻尼系数,试分别列写图示系统的传递函数)()(12s U s U 和)()(12s X s X ,并将其写成典型环节相串联的形式。
2-3试求下图所示有源网络的传递函数。
2-4试用信号流图求出下图所示四端网络的传递函数)()()(12s U s U s G .2-5试绘制下图所示RC 回路的方块图,并根据方块图,并根据方块图写出传递函数)()(s U s U r c 。
2-6 试绘制下图所示电路的结构图,并求传递函数)()(12s U s U 。
2-7 给定一速度调节器的电路如图所示,试求U(s)与)(,)(0s U s U t 之间的关系式。
2-8 下图为由运算放大器组成的控制系统的模拟图,试求其闭环传递函数。
2-9 某RC 网络为下图所示,其中21U U 、分别为网络的输入量和输出量,试求:(1)画出网络相应的结构图(即函数方框图);(2)求传递函数)()(12S U S U (化成标准形式);(3)讨论元件2121,,,C C R R 参数选择是否响应网络的绝对稳定性。
2-10 本题包括以下内容:1.已知由试验得出的环节输出时间特性如下(题图(1)):(1)试确定各环节的传递函数.(2)试确定各环节在s 平面上的零点.极点分部.(3)试画出各环节的伯德(Bode)图.2.设有如下环节(题图(2)):已知: 54321,,,,R R R R R 各为电阻值, 210,,C C C 各为电容值。
(1)试确定各环节的输入与输出的关系。
(2)试画出该环节的结构图。
3.在题图(3)所示系统中,i x :输入位移,0x :输出位移,f:阻尼器的阻尼系数,21k k 、各为弹簧系数.且假定系统是集中参数系统,输出端的负载效应可乎略.试求出图中所示机械系统传递函数。


考研控制工程试题真题及答案# 考研控制工程试题真题及答案## 一、选择题1. 题目:在控制系统中,开环传递函数为\[ G(s) =\frac{10}{s(s+10)} \],问该系统是否稳定?答案:是。
因为开环传递函数的极点s=0和s=-10都位于左半平面。
2. 题目:状态空间表示法中,状态变量的选取具有什么性质?答案:状态变量的选取具有任意性,但一般选择能反映系统动态特性的变量。
3. 题目:PID控制器中的I代表什么?答案:I代表积分(Integral),用于消除系统的稳态误差。
4. 题目:在控制系统设计中,Bode图的主要用途是什么?答案:Bode图主要用于分析系统的频率响应特性,帮助设计系统以满足性能要求。
5. 题目:线性时不变系统(LTI)的数学模型是什么?答案:线性时不变系统(LTI)的数学模型通常为线性微分方程或差分方程。
## 二、简答题1. 题目:简述控制系统的稳定性条件。
答案:控制系统的稳定性条件主要取决于系统开环传递函数的极点位置。
如果所有极点都位于复平面的左半部分,则系统是稳定的。
2. 题目:什么是根轨迹法?答案:根轨迹法是一种控制系统设计方法,通过分析系统开环传递函数的极点随参数变化的轨迹,来设计闭环系统的性能。
3. 题目:控制系统的频率响应特性有哪些?答案:控制系统的频率响应特性包括幅频特性和相频特性,它们描述了系统对不同频率信号的响应能力。
## 三、计算题1. 题目:给定一个二阶系统,其开环传递函数为\[ G(s) =\frac{\omega_n^2}{s^2 + 2\zeta\omega_ns + \omega_n^2} \],其中\[ \omega_n = 10 \] rad/s,\[ \zeta = 0.5 \]。
求系统的单位阶跃响应。
答案:首先确定系统的自然频率\[ \omega_n \]和阻尼比\[ \zeta \]。
然后使用二阶系统的时间响应公式计算单位阶跃响应的表达式。
开环Bode 图的绘制 1关于绘制开环Bode 图的解说教材中有绘制的步骤,熟悉典型环节Bode 图,惯性、一阶微分、振荡环节的近似折线画法的,自然能从阅读步骤中读出味道。
用各环节的高频近似折线绘制开环Bode 图,只能用高频近似表达式,而不能用精确表达式。
因此,必须熟悉惯性、一阶微分、振荡环节的高频近似表达式。
例4.4 设某系统的开环传递函数为⎥⎥⎦⎤⎢⎢⎣⎡+⨯+⎪⎭⎫ ⎝⎛++=1503.0250)141()1101(30)()(2s s s s s s H s G 试绘制其伯德图。
(绘制的图见4.23)解:(1)将开环传递函数中典型环节化为常数项为1的标准形式。
振荡环节也可采用固有频率表示的标准形式;注意,比例环节K 值将会发生变化。
本例的开环传递函数中各环节都是标准形式。
(2)计算K lg 2054.2930lg 20lg 20==K dB(3)开环传递函数中没有积分环节,则绘出K lg 20 dB 的水平直线开环传递函数中有积分环节,则绘出过(ω=1,K lg 20dB)点、斜率为-20dB/dec 的直线。
本例有积分环节,因此过(1,29.5 dB)点b 、斜率为-20dB/dec 的直线,此斜率线即为比例和积分环节对数幅频特性叠加的结果。
(4)从低到高列写各环节的转折频率,并标注在频率轴上。
本例有:惯性环节41=T ω,如图中c 点对应的频率;一阶微分环节102=T ω,如图中d 点的频率;振荡环节503=T ω,如图中e 点的频率;(5)从低到高,在原斜线转折频率对应处,将对应环节高频段近似线的斜率加到原斜线的斜率上,并从该转折频率对应点开始,按叠加所得斜率,绘制斜线,直至下一个环节的转折频率,再按频率叠加方法继续作图。
在本例中:在比例和积分环节叠加的斜线上,找到41=T ω对应的点c ,把惯性环节高频段斜率-20dB/dec 加到原斜率-20dB/dec 上,为-40dB/dec ,从c 点按-40dB/dec 斜率绘制斜线直到,102=T ω的d 点处,叠加上一阶微分环节的斜率,得-20dB/dec ,从d 点出发绘制-20dB/dec 斜率线到503=T ω的e 点处,叠加振荡环节的斜率,得-60dB/dec ,从e 点出发绘制-60dB/dec 斜率线。
例题:已知最小相位系统开环对数频率特性曲线如图所示。
试写出开环传递函数)(s G k 。
解:1) ω<ω1的低频段斜率为[-20],故低频段为K/s。
ω增至ω1,斜率由[-20]转为[-40],增加[-20],所以ω1应为惯性环节的转折频率,该环节为1111+s ω 。
ω增至ω2,斜率由[–40]转为[–20],增加[+20],所以ω2应为一阶微分环节的转折频率,该环节为112+s ω 。
ω增到ω3,斜率由[-20]转为[-40],该环节为1113+s ω,ω>ω3,斜率保持不变。
故系统开环传递函数应由上述各典型环节串联组成,即)11)(11()11()(312+++=s s s s K s G k ωωω2) 确定开环增益K当ω=ωc 时,A(ωc )=1 。
所以 1111)1()1(1)1()(12232122=≈+⋅+=cccc c c c c KK A ωωωωωωωωωωωωω故 12ωωωcK=所以,)11)(11()11()(31212+++=s s s s s G c k ωωωωωω练习:最小相位系统的对数幅频特性如下图所示,试分别确定各系统的传递函数。
(a)(b)(c )a :)1(10)(+=s s s Gb :)1)(110(100)(++=s s s Gc )12.0)(15.0(100)(++=s s s G。
例题:已知最小相位系统开环对数频率特性曲线如图所示。
试写出开环传递函数)(s G k 。
解:
1) ω<ω1的低频段斜率为[-20],故低频段为K/s。
ω增至ω1,斜率由[-20]转为[-40],增加[-20],所以ω1应为惯性环节的转折频率,该环节为
1
1
11
+s ω 。
ω增至ω2,斜率由[–40]转为[–20],增加[+20],所以ω2应为一阶微分环节的转折频率,该环节为
11
2
+s ω 。
ω增到ω3,斜率由[-20]转为[-40],该环节为
1
1
13+s ω,ω>ω3,斜率保持不变。
故系统开环传递函数应由上述各典型环节串联组成,即
)
11
)(
11
(
)11
(
)(3
1
2
+++=
s s s s K s G k ωωω
2) 确定开环增益K
当ω=ωc 时,A(ωc )=1 。
所以 11
1
1
)1
(
)1
(
1
)1
(
)(1
2
23
21
22
=≈
+⋅+=
c
c
c
c c c c c K
K A ωωωωωωωωωωωωω
故 1
2ωωωc
K =
所以,)
11
)(
11
()11
()(3
1
2
12+++=s s s s s G c k ωωωωωω
练习:
最小相位系统的对数幅频特性如下图所示,试分别确定各系统的传递函数。
(a)
(b)
(c )
a :)
1(10
)(+=
s s s G
b :)
1)(110(100
)(++=
s s s G
c )
12.0)(15.0(100
)(++=s s s G。