当前位置：文档之家 › 材料力学第8章应力状态分析

材料力学第8章应力状态分析

  • 格式：ppt
  • 大小：3.55 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

材料力学8-3-平面应力状态分析-课件

材料力学8-3-平面应力状态分析-课件

02
平面应力状态分析的基本概念
应力状态
1 2
定义
应力状态是指物体在某一点处的应力分布情况。
表示方法
通常采用主应力、应力张量和应力矩阵来表示。
3
分类
根据应力分量的变化规律，可分为平面应力状态、 空间应力状态和轴对称应力状态。
平面应力状态
定义
平面应力状态是指物体在某一平面内 的应力分布情况，其应力分量只有三 个，即σx、σy和τxy。
材料力学8-3-平面应力状 态分析-课件
• 引言 • 平面应力状态分析的基本概念 • 平面应力状态的分类与表示 • 平面应力状态的平衡方程与几何方程 • 平面应力状态分析的实例 • 总结与展望
01
引言
平面应力状态分析的定义
平面应力状态分析是材料力学中一个重要的概念，它主要研究物体在受力时，其内 部应力的分布情况。
特点
在平面应力状态下，物体内的剪切力分 量τxy与正应力分量σx、σy成比例关系， 即剪切力分量与正应力分量成正比。
应力分量与主应力
定义
主应力与材料性质的关系
应力分量是指物体在某一点处各个方 向的应力值，而主应力则是应力分量 中的最大和最小值。
主应力的大小反映了材料在该点所受 的应力和应变状态，与材料的弹性模 量、泊松比等性质有关。
应力集中系数
为了描述应力集中的程度，引入了应力集中系数，该系数反映了孔 边应力和平均应力的比值。
弯曲梁的平面应力状态分析
弯曲梁
当梁受到垂直于轴线的力矩作用时，梁发生 弯曲变形。
平面应力状态
在弯曲梁的横截面上，剪应力和正应力的分布情况 。
弯矩和剪力的关系
通过分析剪应力和正应力的分布和大小，可 以确定梁的弯矩和剪力之间的关系，从而进 行受力分析和设计。

周建方版材料力学习题解答[第八章9]分析

周建方版材料力学习题解答[第八章9]分析

8-49现用某种黄铜材料制成的标准圆柱形试件做拉伸试验。

已知临近破坏时，颈缩中心部位的主应力比值为113321::::=σσσ；并已知这种材料当最大拉应力达到770MPa 时发生脆性断裂，最大切应力达到313MPa 时发生塑性破坏。

若对塑性破坏采用第三强度理论，试问现在试件将发生何种形式的破坏？并给出破坏时各主应力之值。

解： 令主应力分别为：σσ31=，σσσ==32脆性断裂时，由第一强度理论=1r σσσ31==770MPa所以，塑性破坏时，由第三强度理论 所以故，试件将发生脆性断裂。

破坏时MPa 7701=σ，MPa 25732==σσ8-50 钢制圆柱形薄壁压力容器（参见图8-13），其平均直径mm d 800=，壁厚mm 4=δ，材料的M P a ][120=σ，试根据强度理论确定容器的许可内压p 。

解：在压力容器壁上取一单元体，其应力状态为二向应力状态。

p pd 504'==δσ ，p pd1002"==δσ 其三个主应力为p 100"1==σσ， p 50'2==σσ，03=σ据第三强度理论所以 ，MPa p 2.13≤，许可内压MPa p 2.13= 据第四强度理论所以，MPa p 39.14≤，许可内压MPa p 39.14=8-51 空心薄壁钢球，其平均内径mm d 200=，承受内压MPa p 15=，钢的MPa ][160=σ。

试根据第三强度理论确定钢球的壁厚δ。

解：钢球上任一点应力状态如图示 其三个主应力为：σσσ==21，03=σ而 MPa MPa d p R R p δδδδππσ4342.0152222=⨯=⋅=⋅⋅=据第三强度理论 所以 mm m 69.41069.41601433=⨯=⨯≥-δ 8-52 图8-77所示两端封闭的铸铁圆筒，其直径mm d 100=，壁厚mm 10=δ，承受内压MPa p 5=，且在两端受压力kN F 100=和外扭矩m kN T ⋅=3作用，材料的许用拉应力MPa ][40=+σ，许用压应力MPa ][160=-σ，泊松比250.=ν，试用莫尔强度理论校核其强度。

材料力学：第八章-应力应变状态分析

材料力学：第八章-应力应变状态分析
斜截面: // z 轴； 方位用 a 表示；应力为 sa , ta
正负符号规定:
切应力 t － 使微体沿顺时针 旋转为正 方位角 a － 以 x 轴为始边、逆时针旋转 为正
斜截面应力公式推导 设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等，同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制 作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍 互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的 应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究 的点, 故通常通过微体, 研究一点处的应力与应变状态

第八章2应力应变状态分析

第八章2应力应变状态分析

第八章2应力应变状态分析应力应变状态分析是研究材料或结构在外力作用下所产生的应力和应变的过程。

应力是单位面积上的内力，用于描述材料或结构对外力的抵抗能力。

而应变是形变相对于初始状态的变化量，用于描述材料或结构的变形程度。

针对材料或结构的应力应变状态进行分析，可以帮助我们了解其力学性能和稳定性，为工程实践提供重要依据。

应力应变状态分析是弹性力学的基本内容之一、根据材料的力学性质和外力的作用，可以得到不同的应力应变状态。

在弹性力学中，线弹性和平面应变假定是常用的简化假设。

线弹性假定材料仅在拉伸和压缩的方向上有应力，而在横截面上的应力是均匀分布的。

一维拉伸和挤压是线弹性应力应变状态的基本类型。

平面应变假定材料在一个平面内有应力，而在垂直于该平面的方向上无应力。

二维平面应变是平面应变应力应变状态的基本类型。

在应力应变状态分析中，我们通常关注应力和应变之间的关系。

最常见的是材料的应力-应变曲线。

应力-应变曲线描述了材料在外力作用下的力学行为，可以帮助我们了解材料的强度、塑性和韧性等性能。

在弹性阶段，应力-应变曲线呈线性关系，符合胡克定律。

而在屈服点之后，材料会发生塑性变形，应力不再是线性关系。

当应力达到最大值时，材料会发生破坏。

除了应力-应变曲线外，还有一些其他重要的参数和指标可用于描述应力应变状态。

例如，弹性模量是描述材料刚度的重要参数，表示单位应力引起的单位应变量。

剪切弹性模量描述了材料抵抗剪切变形的能力。

同时，杨氏模量和泊松比也是用于描述材料力学性质的常用参数。

应力应变状态分析在材料工程、结构工程以及土木工程等领域具有重要应用。

通过对材料和结构的应力应变状态进行分析，可以帮助我们评估其性能和强度，并且对设计和优化具有指导意义。

例如，在结构工程中，通过应力应变状态分析可以确定材料的承载能力和极限状态，从而确保结构在设计荷载下的安全运行。

然而，应力应变状态分析也面临一些挑战。

首先，材料的力学性质和变形行为往往是非线性的，需要使用复杂的数学模型进行描述。

材料力学应力状态分析

材料力学应力状态分析

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科，其中应力状态分析是材料力学中的重要内容之一。

应力状态分析是指对材料内部受力情况进行分析和研究，以揭示材料在外力作用下的应力分布规律和应力状态特征，为工程设计和材料选用提供依据。

本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。

首先，我们来介绍一下应力状态的基本概念。

应力是指单位面积上的力，是描述物体内部受力情况的物理量。

在材料力学中，通常将应力分为正应力和剪应力两种基本类型。

正应力是指垂直于截面的应力，而剪应力是指平行于截面的应力。

在实际工程中，材料往往同时受到多种应力的作用，因此需要对应力状态进行综合分析。

其次，我们将对应力状态进行分类。

根据应力的作用方向和大小，可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。

拉应力状态是指材料内部受到拉力作用的状态，压应力状态是指材料内部受到压力作用的状态，而剪应力状态是指材料内部受到剪切力作用的状态。

这三种应力状态在工程实践中都具有重要的意义，需要我们进行深入的分析和研究。

接下来，我们将介绍应力状态分析的方法。

应力状态分析的方法有很多种，常用的有应力分析法、应变分析法和能量方法等。

应力分析法是通过应力分布的计算和分析来揭示应力状态的特征，应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征，而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。

这些方法各有特点，可以根据具体情况选择合适的方法进行分析。

最后，我们需要注意的是，在进行应力状态分析时，需要考虑材料的本构关系、边界条件和载荷情况等因素，以确保分析结果的准确性和可靠性。

同时，还需要注意应力状态分析的结果对工程实践的指导意义，以便更好地指导工程设计和材料选用。

总之，材料力学应力状态分析是一个复杂而重要的课题，需要我们进行深入的研究和分析。

只有深入理解应力状态的特征和规律，才能更好地指导工程实践，为实际工程问题的解决提供科学依据。

材料力学 第八章：应力状态分析

材料力学 第八章：应力状态分析

2 )2
材料力学
整理可得：
(


x

2
y
)2
2


(
x

2
y
)2
x2
(3)
(3)式为以 、为变量的圆方程。
圆心坐标

(
x
y
,0)
横坐标为平均应力
2
半径

(
x

2
y
)2

2 x
为最大剪应力
材料力学
x x
y
x y
2

(
x

2
y
)2

2 x
材料力学
方法一：
27.5
x

2
y
x
y
2
cos(2 27.5) x
sin(2 27.5)
70 70 cos55 50sin 55 22
96MPa
96MPa
27.5
70MPa
62.5 50MPa 26MPa
117.5

x
上的应力对应-坐标系中的Dy点。Dy
点的横坐标
OF

、纵坐标
y
FDy

y
;连接
Dx、Dy与轴的交点C为圆心 , CDx 或
CDy 为半径画一圆，这个圆是该单元
体所对应的应力圆。
材料力学
n
y

x
y
x
x
y

F o
Dy
(y,y)
Dx(x,x) CK
材料力学
证明：
DxCK DyCF (对顶角) Dy FC DxKC (直角)

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析
1．绘出梁的剪力图和弯矩图；
2．确定梁内横截面上的最大拉应力和最大压应力；
3．确定梁内横截面上的最大切应力；
4．画出横截面上的切应力流。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
1．图（a）：
kN
， kN
剪力与弯矩图如图（b）、（c）；
2．形心C位置
MPa
MPa
3． m3
MPa
4．切应力流如图（e）。
（A）下移且绕点O转动；
（B）下移且绕点C转动；
（C）下移且绕z轴转动；
（D）下移且绕 轴转动。
知识点：弯曲中心、薄壁截面梁产生平面弯曲的加载条件
难度：一般
解答：
正确答案是D。
8－19试判断下列图示的切应力流方向哪一个是正确的。
知识点：横向弯曲时梁横截面上的切应力流、弯曲切应力分析方法
难度：难
解答：
（A）细长梁、横截面保持平面；
（B）弯曲正应力公式成立，切应力沿截面宽度均匀分布；
（C）切应力沿截面宽度均匀分布，横截面保持平面；
（D）弹性范围加载，横截面保持平面。
知识点：弯曲时梁横截面上切应力分析
难度：易
解答：
正确答案是B。
公式 推导时应用了局部截面的正应力合成的轴力，该正应力 则要求弯曲正应力公式成立；另外推导时在 时，应用了 沿截面宽度均匀分布假设。
难度：难
解答：
正确答案是D。
8－21简支梁受力与截面尺寸如图所示。试求N－N截面上a、b两点的铅垂方向的切应力以及腹板与翼缘交界处点c的水平切应力。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
FQ = 120kN，形心C位置。

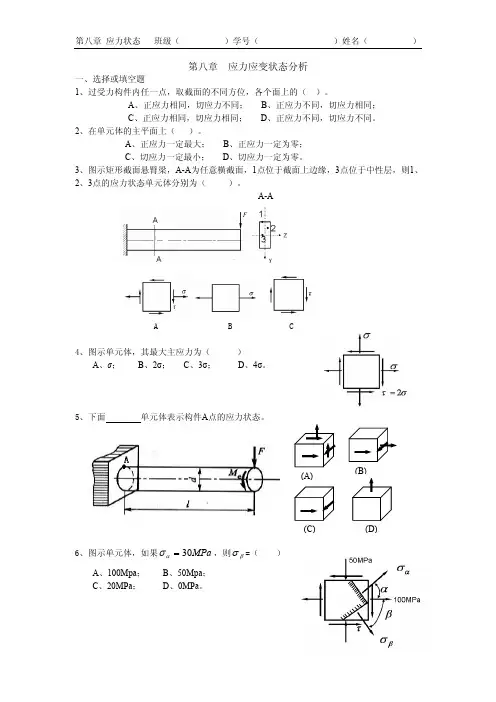
材料力学作业(8-11)

材料力学作业(8-11)

第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点，取截面的不同方位，各个面上的（ ）。

A 、正应力相同，切应力不同；B 、正应力不同，切应力相同；C 、正应力相同，切应力相同；D 、正应力不同，切应力不同。

2、在单元体的主平面上（ ）。

A 、正应力一定最大；B 、正应力一定为零；C 、切应力一定最小；D 、切应力一定为零。

3、图示矩形截面悬臂梁，A-A 为任意横截面，1点位于截面上边缘，3点位于中性层，则1、2、3点的应力状态单元体分别为（ ）。

A-AA B C4、图示单元体，其最大主应力为（ ）A 、σ；B 、2σ；C 、3σ；D 、4σ。

5、下面 单元体表示构件A 点的应力状态。

6、图示单元体，如果MPa 30=ασ，则βσ=（ ） A 、100Mpa ； B 、50Mpa ； C 、20MPa ； D 、0MPa 。

(C)7、图示单元体应力状态，沿x 方向的线应变εx 可表示为（ ）A 、Eyσ； B 、)(1y x E μσσ−；C 、)(1x y E μσσ− ；D 、Gτ。

8、图示应力圆对应于单元体( )。

9、已知单元体及应力圆如图所示，σ1所在主平面的法线方向为( )。

A 、n 1；B 、 n 2；C 、n 3；D 、n4。

二、计算题1、已知应力状态如图所示，试用解析法计算图中指定截面上的正应力和切应力。

2、试画图示应力状态的三向应力圆，并求主应力、最大正应力和最大切应力。

3、边长为20mm的钢立方块置于刚性模中，在顶面受力F=14kN作用。

已知材料的泊松比为0.3，求立方体各个面上的正应力。

4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m，Q=120 kN。

试绘出截面上1、2、3、4各点的应力状态单元体，并求其主应力。

第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下，水管中的水会受冻而结冰。

根据低温下水管和冰所受力情况可知（ ）。

A 、冰先破裂而水管完好；B 、水管先破裂而冰完好；C 、冰与水管同时破裂；D 、不一定何者先破裂。

材料力学(单辉组)第八章应力应变状态分析

材料力学(单辉组)第八章应力应变状态分析

由
tan
2a0

2t x sx s
y
得
cos 2a0
sx sy
2

s
x
s
2
y
2

t
2 x
sa

sx
sy
2

sx
s y
2
cos 2a
t x
sin 2a
最大和最小正应力(主应力)
s max s min

sx
sy
2


sx
s
2
y
2

t
2 x
应力状态：通过一点所有微截面上应力状况 应变状态：通过一点所有微截面上应变状况
6
如何描述复杂状态？ 微体法：---关注一点 一点的应力状态(静力学关系) 一点的应变状态(几何关系) 二者之间的联系(物理关系) 能量法: 应变能---关注整体
目的：解决复杂状态下的强度、刚度、稳定性
7
微体法
• 平面应力状态
T
T
s1 0，s2 0，s3 =0
• 空间应力状态
F
s1 0，s2 0，s3 0
11
EX1 画出矩形梁在滑动铰支座
右侧横截面内不同点的应力状态 F
y
1
1
Fs
2
2
z
M
3
3
4
5
4
s M z y t FSSA1( y)
Iz
Izb
5
12
EX2 画出螺旋桨轴杆表面一点的应力状态
由上式可得相差为900的两个a0值，在这两个相
互垂直的截面上，正应力取得最大值和最小值;

高等教育出版社简明材料力学第二版 第八章 应力状态分析和强度理论分析

高等教育出版社简明材料力学第二版 第八章 应力状态分析和强度理论分析

1 150 MPa, 2 75 MPa,
3 0
2018/10/12 15
8-2 二向和三向应力状态的实例
火车车轮与钢轨的接 触点也是三向应力状态
A
滚 珠 轴 承
2 A
3
1
2018/10/12
16
第八章
应力状态分析和强度理论
§8-1 应力状态的概述 单向拉伸时斜截面上的应力 §8-2 二向和三向应力状态的实例 §8-3 二向应力状态分析 §8-4 二向应力状态的应力圆 §8-5 三向应力状态简介 §8-6 广义胡克定律 §8-7 复杂应力状态下的应变能密度 §8-8 强度理论概述 §8-9 四种常用强度理论
则斜截面面积为： A Aα = cos α F F cosα F pα cos σ cosα Aα A A
σ σα = pα cosα =σ cos α τ α = pα sin α = σ sin α cos α = sin 2α 2
2
直杆拉伸应力分析结果表明：即使同一点不同方向面 上的应力也是各不相同的，此即应力的面的概念。
10
第八章
应力状态分析和强度理论
§8-1 应力状态的概述 单向拉伸时斜截面上的应力 §8-2 二向和三向应力状态的实例 §8-3 二向应力状态分析 §8-4 二向应力状态的应力圆 §8-5 三向应力状态简介 §8-6 广义胡克定律 §8-7 复杂应力状态下的应变能密度 §8-8 强度理论概述 §8-9 四种常用强度理论
8-3 二向应力状态分析
考虑到切应力互等定理：τxy=τyx


xy
x y



yx

x y
x y

应力状态分析和强度理论

应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态，当超过这一极限时，材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时，其内部应力状态会发生变化，当达到某一特定应力状态时，材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态，当超过这一极限时，材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服（即非弹性变形）的应力状态，是材料强度分析的重要依据。
根据不同的材料特性，存在多种屈服条件，如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示，用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据，当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时，材料会发生屈服和塑性变形，导致失效。该准则适用于韧性材料的失效分析，尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环，主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线，并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响，因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。

材料力学-应力状态与应变状态分析

材料力学-应力状态与应变状态分析

s2 引起 1 s 2 E 2 s 2 E 3 s 2 E
s3 引起 1 s 3 E 2 s 3 E 3 s 3 E
小变形 i i i i i 1,2,3
1
1 E
s1
(s 2
s 3 )
广
2
1 E
s 2
(s 3
s1 )
义 虎 克 定
3
1 E
s 3
(s 1
s 2)
t T ＝ 1 πD3 (1－a4) 16
1
＝
1 E
[s1－
(s2＋s3)]
＝
1＋
E
t
T＝8.38 kN·m
二、体积应变
单元体边长：dx、dy、dz
体积：V0 = dx·dy·dz
dy
dx → dx +△dx = dx + 1dx = (1 + 1) dx
dy → dy +△dy = dy + 2dy = (1 + 2) dy
体积的绝对增量：△V = V－V0 = V0 (1+ 2+ 3)
单位体积增量：
V V0
1 2
3
体积应变 体积的相对增量
1 2
E
(s1
s2
s
3)
讨论：
V V0
1 2
E
(s1 s 2
s 3)
⒈ 若 s1 + s2 + s3＞0，
则 ＞0 →△V ＞0，即体积增大；
若 s1 + s2 + s3＜0，
s2
s3 dsz 1
dx
dz → dz +△dz = dz + 3dz = (1 + 3) dz

工程力学材料力学之应力应变状态分析

工程力学材料力学之应力应变状态分析
工程力学材料力学之应力应变状态分 析
二、材料破坏的两种类型（常温、静载荷） (Two failure types for materials in normal temperature and static loads)
1. 断裂失效(Fracture failure) （1）脆性断裂 : 无明显的变形下突然断裂. （2）韧性断裂 : 产生大量塑性变形后断裂.
剪切
扭转
工程力学材料力学之应力应变状态分 析
上述强度条件具有如下特点： (1)危险点处于单向应力状态或纯剪切应力状态； (2)材料的许用应力 ，是通过拉(压)试验或纯剪试验测定试 件在破坏时其横截面上的极限应力,以此极限应力作为强度指 标,除以适当的安全系数而得，即根据相应的试验结果建立的 强度条件.
胡克（1635-1703）
波义耳（1627-1691）
惠更斯（1629-1695）工程力学材料力学牛析之顿应力（应1变64状3态-分1727）
复杂应力状态的应变能密度
三向应力状态
体积改变能密度 畸变能密度
工程力学材料力学之应力应变状态分 析
§7-8 强度理论(The failure criteria)
构件每单位体积的体积变化, 称为体积应变用θ表示.
各向同性材料在三向应力状态下的体应变
如图所示的单元体，三个边长为 a1 , a2 , a3 变形后的边长分别为
a1(1+，a2(1+2 ，a3(1+3
变形后单元体的体积为
2
a2
1
3
a1
a3
V1=a1(1+·a2(1+2 ·a3(1+3
工程力学材料力学之应力应变状态分 析
二向应力状态下(In plane stress-state) 设 3= 0

材料力学课件 第八章应力状态与强度理论

材料力学课件 第八章应力状态与强度理论
二向应力状态（Plane State of Stress）： 一个主应力为零的应力状态。
单向应力状态（Unidirectional State of Stress）： 一个主应力不为零的应力状态。
x B x
zx
xz
x
x
A
§8–2 平面应力状态下的应力分析
y
y
y
xy x
等价 y
x
xy
x z
Ox
一、解析法
30
x
y
2
sin 2
x cos2
80 (40) sin(2 30 ) 60 cos(2 30 ) 2
21.96MPa
确定主平面方位，将单元体已知应力代入 8.3，得
20 45
tan 20
2 x x y
2 (60) 80 (40)
1
0 22.5
0 即为最大主应力1 与 x 轴的夹角。主应力为
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane)：
剪应力为零的截面。 x
主应力(Principal Stress ）：
主平面上的正应力。
1
主应力排列规定：按代数值大小，
1 2 3
三向应力状态（ Three—Dimensional State of Stress）： 三个主应力都不为零的应力状态。
解：由于主应力1 ，2 ，3 与主应变1 ，2 ，3 一一对应，故由已知数据可知，
已知点处于平面应力状态且 2 0 。由广义胡克定律
1
1 E
(1
3 )
3
1 E
( 3
1)
联立上式

北航 材料力学 第八章 应力状态分析

北航 材料力学 第八章 应力状态分析

应力应变状态分析
y
y x
§8-2
y
dx dy
平面应力状态应力分析
什么是平面应力状态？
x
dz
x
•微体有一对平行表面不受力的应力状态。 由此推断
x
微体仅有四个面作用有应力； 应力作用线均平行于不受力表面； 平面应力状态的应力分析 问题：已知x , y, x , y, 求任 意平行于z轴的斜截面上的应力。
Page 2
第八章
应力应变状态分析


关于微体：
围绕杆件内某点所截取的一个边长无限小的长方体； 每个面上的应力分布差异可忽略，认为其均匀分布；
微体相对的两个面上的应力视为过该点的、法向相反的两 个平面在该点的应力，等值、反向 ； 微体三个相邻表面上的应力分别代表了过该点的、互相垂 直的三个平面在该点的应力状况； 微体的任意截面上的应力均匀，并且代表了同法向平面在 该点的应力
第八章
应力应变状态分析
第八章
§8-1 §8-2
应力应变状态分析
引言 平面应力状态应力分析
§8-3
§8-4 §8-5 §8-6 §8-7 §8-8
应力圆
平面应力状态的极值应力与主应力 复杂应力状态的最大应力 平面应变状态应变分析 各向同性材料的应力、应变关系 复杂应力状态下的应变能与畸变能
§8-9
复合材料的应力、应变关系
纯剪切受力状态
y
应力应变状态分析
单向受力状态
x x
双向等拉

x

R=x
R=x/2 o
C
C

o

o

x/2
Page16
第八章

材料力学08应力状态理论

材料力学08应力状态理论

1.公式推导：
Fin 0 ,
sa dA s xdA cos2 a t xydA cosa sina
s ydAsin2 a t yxdAsina cosa 0
sa
同理， Fit 0, ta
2.任意a斜截面上的应力公式
sa

sx
sy
2
sx
s y
2
cos2a

1 2
s11
等于所示阴影部分面积
切应力的极值作用面与正应力
的极值作用面互成 45o的夹角
t max
s
(
x
s
2
y
)2
t
2 xy
s max
s min
2
min
极值切应力作用面上的正应力：
s0
s0900
sx
sy
2
5.平面应力状态分析的特征 1）斜截面应力、主应力及最大切应力均是指 xy 平面内的应 力，即其作用面均垂宜于 xy 平面。 2)任意两相互垂直截面上的正应力之和为常量
sa0 及sa0900的方向是相互垂直的。其中，a0由sin2a0和cos2a0的
正负号唯一地确定。
3.正应力极值——主应力
sa0
a0 900
s max
min
sx
sy
2

sx

s
2
y
2

t
2 xy
又，ta0 0 极值正应力就是主应力！
a0 900
smax的指向是介于仅由单
2.纯剪切平面应力状态
V

1
2
E
(s
1

材料力学应力分析

材料力学应力分析

应力状态
-
yx
即又一次证明了切应力的互等定理。
xy
y
§2 平面应力状态分析
应力状态
３、平面应力状态的极值与主应力
x
+ y
2
+ x
- y
2
cos 2
- xy sin 2
x
- y
2
sin 2
+ xy cos 2
x
- y sin
2
tan 20
2 -
+ xy cos 2 xy
x - y
2＝0
得到xy 的极值
＝ 1 2
x
- y
2
+
4
2 xy
应力状态
需要特别指出的是，上述切应力极值仅对垂直 于xy坐标面的方向面而言，因而称为面内最大切应 力与面内最小切应力。二者不一定是过一点的所有 方向面中切应力的最大和最小值。
§2 平面应力状态分析
应力状态
过一点所有方向面中的最大切应力
为确定过一点的所有方向面上的最大切应力，可以
(
-
x
+
2
y
)
x
-
2
y
cos 2
-
xy
sin
2
(1)
x
- y
2
sin 2
+ xy
cos 2
x
- y
2
sin 2
+ xy cos 2
(2)
§2 平面应力状态分析
应力状态
(
-x
+ y
2
)2
+
2
a( a , a )

材料力学：ch8 应力应变状态分析

材料力学：ch8 应力应变状态分析

泊松比 = 0.33。试求板厚的改变量 与板件的体积改变量 V 。
题 8-16 图
6
解：此为平面应力状态问题。设板厚度方向的正应变为 εz ，则有
εz
μ E
(σ x
σ
y
)
板厚的改变量为
Δδ
z
E
(σ x
σy
0.33 0.010 70 109
(80
40) 106 m
1.886 106 m 0.001886mm
σ1 69.7MPa， σ2 9.9MPa 由于是平面应力状态，故知
σ3 0 从该应力圆上还可以量得 σ1 的方位角为
α0 23.7 式中负号表示从 AB 面的外法线沿顺时针方向旋转。
8-9 图示悬臂梁，承受载荷F = 20kN作用，试绘微体A，B与C的应力图，并确定主应
力的大小及方位。
题 8-9 图 解：由题图可知，指定截面的剪力与弯矩分别为
)
51.7
MPa
7
60
100 80 2
100 2
80
cos(120
)
50
sin(120
)(
MPa
)
128.3
MPa
根据广义胡克定律，得 30°的正应变为
30
1 E
( 30
60 )
200
1 109
Pa
(51.7
106
Pa
0.3128.3106
Pa
)
0.66
10
4
8-18 构件表层一点处的应力如图a所示，为了测量应力，在该点沿 0°，45°与 90°
根据平面应力状态的广义胡克定律，有
x
E 1 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

点。设想以A点为中心，用相互垂直的6个截面截取一个边长无限小的立方
体，我们将这样的立方体称为单元体。取决于截取平面的倾角变化，围绕同 一个点，可以截取出无数个不同的单元体，
图8.1（b）为依附着杆件横截面所截取单元体(图8.1（c）为其平面图形式)，而 图8.1（d）为依附着45°斜截面所截取的单元体。由于杆件轴向拉伸时，横 截面上只有正应力，且与杆件轴向平行的截面没有应力，因此，图8.1（b） 中的单元体只在左右两个面上有正应力作用。对于图8.1（d）中的单元体， 根据拉压杆斜截面应力分析（2.3节）可知，其4个面上既有正应力又有切应 力。
又有切应力。围绕A，B，C三点截取单元体如图8.2(d)所示，单元体的前后
两面为平行于轴线的纵向截面，在这些面上没有应力，左右两面为横截面的 一部分，根据切应力互等定理，单元体B和C的上下两面有与横截面数值相等
的切应力。至此，单元体各面上的应力均已确定。注意到图8.2（d）各单元
体前后面上均无应力，因此也可用其平面视图表示(见图8.2（e）)。
图8.2
从受力构件中截取各面应力已知的单元体后，运用截面法和静力平衡条件， 可求出单元体任一斜截面上的应力，从而可以确定出极值应力。
围绕构件内一点若从不同方向取单元体，则各个截面的应力也各不相同。其
中切应力为零的截面具有特殊的意义，称为主平面；主平面上的正应力称为 主应力。一般情况下，过构件内任一点总能找到3个互相垂直的主平面，因
图8.3
运用截面法可以求出与 z 截面垂直的任意斜截面 ac 上的应力（见图 8.3
（ a ））。设斜截面 ac 的外法线 n 与 x 轴的夹角为 α （斜截面 ac 称 为 α 截面），并规定从 x 轴正向逆时针转到斜截面外法线 n 时 α 角为正
（见图 8.3 （ b ）），反之为负。沿 α 截面将单元体截分为两个部分，保
即
以α 0表示极值正应力作用平面的法线与x轴的夹角，从而可求得
将式(8.4)与式（8.2）比较可见，极值正应力作用的截面上切应力为零，因 此，极值正应力作用的平面即为主平面，因此式（8.4）即为主平面倾角表
达式。
因为 tan 2α 0=tan 2(α
0
+ 90°)，所以方程（8.4）有两个解α 0和α ′0
=α 0+ 90°，它们确定了互相垂直的两个主平面的方位，在这两个主平面上
同时作用有正应力的极值，一个为极大值，另一个为极小值。由公式(8.4) 求出sin 2α 0，cos 2α 0，sin 2α ′0及cos 2α ′0，代入公式(8.1)中，则
正应力极大值和极小值为
由于这两个正应力极值，作用在主平面上，因此这两个正应力 极值即为两个主应力，式（8.5）即为平面应力状态主应力计算
式。由于平面应力状态中有一个主应力为零，因此3个主应力分
别为式（8.5）计算得到的σ
留左下部分， α 截面上的正应力和切应力分别用 σ α 和 α 表示，如图 8.3 （ c ）所示。若斜截面 ac 的面积为 A α ，则 ab 面和 bc 面的面积分别为 A α
cos α 和 A α sin α 。考虑左下部分的平衡，列法线 n 和切线 t 方向的
平上相等，以
图8.1
由以上分析可见，杆内各点应力的大小和方向不仅与该点所处位置有关，而
且还与过该点的截面方位有关。过一点所有截面上应力的集合，称为该点的
应力状态。为了解决构件在复杂受力情况下的强度问题，必须了解构件中的 危险点哪一截面的正应力最大，哪一截面的切应力最大，为此有必要研究一
点处各截面应力的变化规律，这就是一点的应力状态分析。一点的应力状态
第8章 应力状态分析
8.1应力状态概述 在研究杆件弯曲或扭转变形时，杆件内位置不同的点具有不同的应力情况。
因此，构件中某一点的应力随几何坐标变化，是几何坐标的函数。然而，即
使对空间位置确定的某一个点而言，通过该点的截面方位不同，其应力值也 不相同。现在以直杆拉伸为例（见图8.1），A点是杆件中位置确定的一个
向（或空间）应力状态，当有一个主应力为零时，称为二向（或平面）应力
状态，当有两个主应力为零时，称为单向应力状态。三向和二向应力状态又 称为复杂应力状态，单向应力状态则称为简单应力状态。
工程中经常遇到二向应力状态的问题，下面主要对二向应力状态进行分析研
究。
8.2二向应力状态分析——解析法 8．2．1二向应力状态的斜截面应力 如图8.3（a）所示单元体为二向应力状态的一般情况，在单元体上，与 x 轴垂直的平面称为x截面，其上作用有正应力σ x和切应力x；与y轴垂直的平 面称为y截面，其上作用有正应力σ y和切应力y；与z轴垂直的z截面上应力为 零，该平面是主平面。切应力x 或y的角标x(或y)表示切应力作用面的法线 方向。二向应力状态也可用如图8.3（b）所示的平面单元体来表示。应力的 符号规则如前（参见2.3节），图中的σ x，σ y和x为正值，而y为负值。
而存在3个主应力，这3个主应力按代数值排列分别表示为 σ 1，σ 2，σ 3，
按代数值大小排序，它们的关系为σ 1≥σ 2≥σ 3。3个相互垂直的主平面可 围成一个单元体，自然，该单元体各个面均为主平面，且该单元体上只有主
应力的作用，这样的单元体称为主单元体。
对于构件中的某一点，当3个主应力全都不为零时，该点的应力状态称为三
通常用单元体来描述。
在分析构件中一点的应力状态时，通常先用应力已知的截面来截取一个单元
体。例如，如图8.2（a）所示的悬臂梁，在横截面m—m上A，B，C这3点的应
力（见图8.1（b））可由弯曲应力公式确定。由应力沿截面高度的变化规律 （见图8.2（c））可知，A点只有正应力，B点只有切应力，C点既有正应力
x代替
y利用三角公式，上两式可简化为
利用式（8.1）和式（8.2）可求得二向应力状态单元体上任意斜截面上的应
力σ
α
和
8．2．2主平面与主应力的计算 由公式（8.1）可知，斜截面上的正应力σ
α
的数值随角度α 而改变，极值正
应力的数值及与之对应的斜截面法线与 x 轴的夹角，可由公式（8.1）通过
导数 求得。