当前位置：文档之家 › 分子几何构型判断3

分子几何构型判断3

  • 格式：ppt
  • 大小：734.00 KB
  • 文档页数：69

下载文档原格式

  / 69

合集下载

高中杂化轨道判断技巧

高中杂化轨道判断技巧

高中杂化轨道判断技巧杂化轨道是化学中的一个重要概念，它描述了原子中电子云的一种混合状态。

在高中化学中，学生需要掌握杂化轨道的概念，并能够判断分子中原子的杂化轨道类型。

本文将介绍几种高中杂化轨道判断技巧，帮助学生更好地掌握这个概念。

一、根据分子几何构型判断杂化轨道类型分子几何构型是指分子中原子的空间排列方式。

在杂化轨道理论中，不同的分子几何构型对应着不同的杂化轨道类型。

因此，通过观察分子几何构型，我们可以初步推断原子的杂化轨道类型。

例如，当分子几何构型为线性时，我们可以判断其中原子的杂化轨道为sp；当分子几何构型为三角形平面时，我们可以判断其中原子的杂化轨道为sp2；当分子几何构型为四面体时，我们可以判断其中原子的杂化轨道为sp3。

二、根据分子中原子的电子数判断杂化轨道类型在分子中，原子的杂化轨道类型还可以通过观察其电子数来判断。

通常情况下，一个原子的杂化轨道类型取决于其原子轨道中存在的电子数。

例如，当一个原子的s轨道和两个p轨道中共有四个电子时，我们可以判断其杂化轨道类型为sp3。

当一个原子的s轨道和一个p轨道中共有两个电子时，我们可以判断其杂化轨道类型为sp。

三、根据分子中原子的化学键数判断杂化轨道类型在分子中，原子的杂化轨道类型还可以通过观察其与其他原子形成的化学键数来判断。

通常情况下，一个原子的杂化轨道类型取决于其与其他原子形成的化学键数。

例如，当一个原子与三个其他原子形成共价键时，我们可以判断其杂化轨道类型为sp3。

当一个原子与两个其他原子形成共价键时，我们可以判断其杂化轨道类型为sp2。

四、根据分子的反应活性判断杂化轨道类型在分子中，原子的杂化轨道类型还可以通过观察其反应活性来判断。

通常情况下，原子的杂化轨道类型与其反应活性有关。

例如，当一个原子的杂化轨道为sp3时，其反应活性通常较低。

而当一个原子的杂化轨道为sp时，其反应活性通常较高。

总结杂化轨道是化学中的一个重要概念，学生需要掌握其概念和判断方法。

分子几何构型

分子几何构型

分子几何构型
分子几何构型是指分子中原子在空间的相对排列关系。

不同的分子几何构型对应于不同的化学键和键长、键角等参数。

了解分子几何构型对于了解物质的性能与其内部结构的关系具有十分重要的意义。

常见的分子几何构型包括直线型、平面正三角形、正四面体、三角锥形、折线形、平面形、折面形、平面正四边形、正四面梯形等。

这些构型可以通过实验测定的键长、键角等数据来确定。

在理论化学中，可以使用理论方法预测分子的几何构型。

例如，价键理论（VB理论）可以用线性变分法处理H₂分子，得到三个等同的sp2杂化轨道，形成平面正三角形的构型。

此外，分子轨道理论也可以用来预测分子的几何构型。

总之，分子几何构型是化学键和分子结构研究的重要内容之一，对于理解物质的性质和反应机理具有重要意义。

选修二2.2.3 解题策略 分子的空间结构及判断方法

选修二2.2.3 解题策略 分子的空间结构及判断方法


sp
1个ns和 1个np
轨道夹角 180°
实例
CO2
sp2
1个ns和 2个np
120°
BF3
sp3
1个ns和 3个np
109°28 ′ CH4
【典例1】下列分子中,中心原子杂化轨道类型相同,分子的空间结构也相
同的是( )
A.H2O、SO2 答案 B
B.BeCl2、CO2
C.H2O、NH3
D.NH3、CH2O
VSEPR模型
分子或离子的立体构型。
2.确定分子或离子的立体构型。
①若中心原子A无孤电子对,则分子或离子的立体构型为价层电子对的立体构
型—VSEPR模型。
②若中心原子A有孤电子对,则分子或离子的立体构型为略去中心原子孤电子
对后的成键电子对的立体构型。
【三言两语话重点】
(1)1个公式:
1
中心原子的价层电子对数=σ键电子对数+ 2 (a-xb)。
空间结构 间结构
直线形 直线形
三角形
三角形 V形
正四面体形
四面体形 三角锥形
V形
实例
BeCl2 BF3
SnBr2 CH4 NH3 H2O
3．利用键角判断 一般来说，高中阶段知道了多原子分子中的键角数据，就可确 定该分子的空间几何构型。常见分子的键角与分子构型如下表：
分子 硫化氢
水
氨
甲烷
二氧化碳
键角 约90° 105°
107° 109°28′
180°
分子构型 V形
V形 三角锥形 正四面体形 直线形
分子 白磷 三氯化硼 乙烯
乙炔
苯
键角 60° 120°
120°
分子或离子空间构型的判断方法

分子或离子空间构型的判断方法

分子或离子空间构型的判断方法
1.空间构型的可解析法：根据分子或离子的几何构型和化学键的长度、角度以及存在的非共面情况，可以通过几何推算来判断其空间构型。

例如
在VSEPR理论中，根据中心原子周围键的种类和数量以及孤对电子的影响，可以预测分子的空间构型。

2.实验技术法：通过实验手段来确定分子或离子的空间构型。

例如，
X射线晶体学可以通过测定晶体中原子的位置来确定其空间构型。

3.分子模拟法：借助于计算机模拟和量子化学计算的手段，可以通过
分子力场、量子力学计算等方法来预测分子或离子的空间构型。

这种方法
可以考虑更多的因素，如电荷分布和随机热运动的影响，从而更准确地判
断空间构型。

4.光谱技术法：在分子或离子存在谐振，激发或振动的情况下，通过
观察其产生的光谱特性，如红外光谱、拉曼光谱等，可以得出分子或离子
的空间构型信息。

以上是几种常用的判断分子或离子空间构型的方法，不同的方法在实
际应用中有其适用范围和局限性。

对于一些简单的分子和离子，几何推算
方法通常可以给出较为准确的空间构型信息。

而对于复杂的大分子和离子，分子模拟和实验技术往往是更可靠和准确的方法。

通过综合运用这些方法，可以对分子和离子的空间构型进行全面的判断和研究。

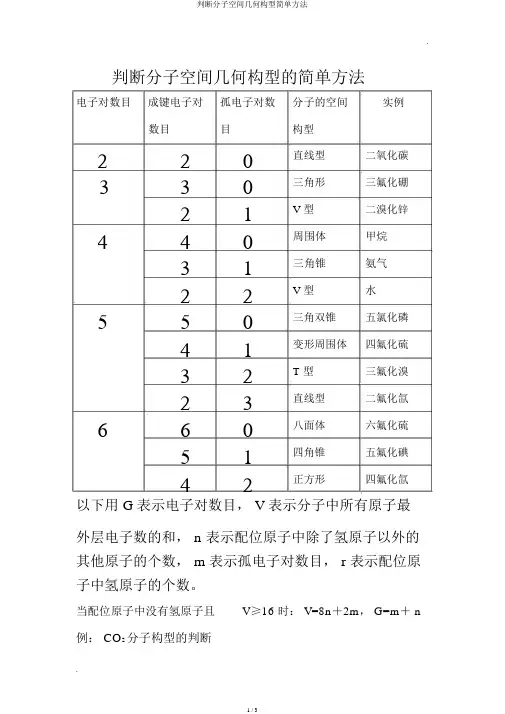
判断分子空间几何构型简单方法

判断分子空间几何构型简单方法

判断分子空间几何构型的简单方法电子对数目成键电子对孤电子对数分子的空间实例数目目构型220 33021 4403122 550413223 6605142直线型二氧化碳三角形三氟化硼V 型二溴化锌周围体甲烷三角锥氨气V 型水三角双锥五氯化磷变形周围体四氟化硫T 型三氟化溴直线型二氟化氙八面体六氟化硫四角锥五氟化碘正方形四氟化氙以下用 G表示电子对数目， V 表示分子中所有原子最外层电子数的和， n 表示配位原子中除了氢原子以外的其他原子的个数， m表示孤电子对数目， r 表示配位原子中氢原子的个数。

当配位原子中没有氢原子且V≥16 时： V=8n＋2m， G=m＋ n 例： CO2分子构型的判断V=4＋ 6× 2=8n＋ 2m，这里 n=2，∴ m=0,∴ G=m＋ n=0＋2=2，所以 CO2的分子构型为直线型BF3分子构型的判断V=3＋ 7× 3=8n＋ 2m，这里 n=3，∴ m=0,∴ G=m＋ n=0＋3=3，所以 BF3的分子构型为三角形PCl5分子构型的判断V=5＋ 7× 5=8n＋ 2m，这里 n=5，∴ m=0,∴ G=m＋ n=0＋5=5，所以 PCl5的分子构型为三角双锥SF4分子构型的判断V=6＋ 7× 4=8n＋ 2m，这里 n=4，∴ m=1,∴G=m＋ n=1＋4=5，所以 SF4的分子构型为变形周围体BrF3分子构型的判断V=7＋ 7× 3=8n＋ 2m，这里 n=3，∴ m=2,∴G=m＋ n=2＋3=5，所以 BrF3的分子构型为 T 型SF6分子构型的判断V=6＋ 7× 6=8n＋ 2m，这里 n=6，∴ m=0,∴ G=m＋ n=0＋6=6，所以 SF6的分子构型为八面体XeF4分子构型的判断V=8＋ 7× 4=8n＋ 2m，这里 n=4，∴ m=2,∴G=m＋ n=2＋4=6，所以 XeF4的分子构型为正方形当配位原子中有氢原子且 V＜ 16 时： V=2r ＋ 8n ＋ 2m，G=m＋ n＋ r 。

价电子对互斥理论（VSEPR）与分子几何构型

价电子对互斥理论（VSEPR）与分子几何构型

价电子对互斥理论(VSEPR )与分子几何构型（原载《结构化学问题选讲》，杨宗璐等编，科学出版社2000年）多原子分子的结构比双原子分子要复杂得多，因此一般需要用一组键长和键角的数据来表征其几何构型.原则上可以通过越来越多的计算方案来求解波动方程，得到所需的结合能、平衡几何构型和电荷密度.另一方面，针对大量的复杂分子，人们总是力图采用简化的模型和图象来推理和总结多原子分子中电子行为的规律.价电子对互斥理论（VSEPR ）正是这样一种简明、直观、可广泛预测许多简单多原子分子结构的一种方法.价电子对互斥理论（VSEPR ）实际上是建立在定域模型基础上的静电理论.按照定域键模型，分子中的电子可划分为：内层电子、孤对电子及成键电子（价电子）等独立组份.分子的能量则与这些独立组份能量及它们的相互作用有关.通过核间距的调整使键长和键角的相互适应，产生了能量最低的几何结构.此外，价电子的分布又受到Pauli 不相容原理和静电库仑作用的支配，除了要求分子中的电子尽量配对外，为使体系电子云分布具有能量最低值，还要求已配对的电子之间彼此尽可能远离，以降低库仑排斥作用.以ALmEn 代表多原子分子，其中A 为中心原子，L 为配位原子，E 则为A 原子价层上的孤对电子对，m 为价层总电子对数P，则可借上述价电子互斥理论提出判断分子几何构型的以下规则：n +1.一定数目的价电子对必定与一定的几何构型相联系.假定价电子对的中心与原子A的距离都是R，为使彼此间斥力最小，价电子对等距离地排布在以R为半径的球面上，形成规则的多面体.根据立体几何的知识，当P为2时，呈直线形（键角为180o）；P为3 时呈平面三角形（键角为120o）；P为4时呈四面体形（键角为10928′o ）；P为5时呈三角双锥形；P为6时呈八面体形；P为7 时则呈五角双锥形等.2. 价电子对互斥理论将分子的共价双键或三重键均视为一个电子对来计算.由于多重键中的电子对数多，占据的空间比一个单键电子对大，它对其它单键电子对的排斥作用较强，使分子中含多重键的键角变大，不同键电子对之间排斥作用的大小顺序为三键排斥＞双键排斥＞单键排斥显然，多重键的存在会影响分子的几何构型.例如 X 2C=0 型分子属于三角形构型，各键角标准值应为120o，不含双键的键角受到前者的影响应小于120o .具体实例见表1.表1 键角的比较X2C=0 ∠XCO ∠XCXF2C=0 123.20112.50Cl2C=0 124.30111.30H2C=0 1210118.00(NH2)2 C =0 1210118.00X2C=CX2∠XCX ∠XCCH2C=CH2116.60121.70(CH3)2C=CH2109012503.用于推测分子结构时，不能忽略孤对电子和成键电子的区别.因为孤对电子对比键电子对更集中于原子核附近，因而增加了排斥能.此外，成键电子对于两个原子核的吸引，电子云显得不如孤对电子的“肥大”，对邻近电子对的斥力也小.孤对电子与键对电子间的排斥强度符合以下排序：孤对/孤对＞孤对/键对＞键对/键对.一般情况下，由于孤对与键对的不同取向可形成一组异构构型，以上的排斥作用顺序可以帮助辨认能量最低的稳定构型.当某个构型中孤对与孤对的交角小于或等于90o，则必定是不稳定构型.例如，ICl4-的6对价电子对指向正八面体6个顶点，由于只有二对孤对电子，故可形成两种不同的异构构型（见图1）.在平面正方形的构型中，两对孤对电子相距最远，应为稳定构型.又如，在SF4，ClF3和IF2-的价电子层中，价电子对数P均为5,但孤对电子对数分别为1、2、3.根据价电子对互斥理论，孤对电子对应选择赤道方向的位置，这样可使与孤对电子对互成90o相互作用的键对数目最少.从图2可知，在它们各自的最稳定构型中，孤对电子对均处于三角平面内.4. 配位原子的电负性增大或中心原子电负性减小，也会使键角偏离标准值.端原子电负性增加时，共享电子对将偏向配位体，从而减少成键电子对之间的斥力，键角的度数随之减小.例如OF2的键角(103.2o)比OH2的键角(104.5o)要小.NF3的键角(102o)比NH3的键角(107.3o)也要小.此外，中心原子的半径增大使与端原子之间的键长增加，减小键电子对之间的排斥力，使键角缩小.实例参见表2.表2 键角的比较分子式 键角 分子式 键角NH3107.30H2O 104.50PH393.30H2S 92.20AsH391.80H2Se 91.00SbH391.30H2Te 89.005.价电子对的相邻电子对越多，所受斥力就越大，距离原子核也越远.当配位数为5和7时，分子呈三角双锥和五角双锥构型，这时主轴上两对电子受到的斥力较大，因而键长较长.例如PCl5分子中，垂直方向的键长为219pm，水平方向键长为204pm，见图3.价电子对互斥理论能够广泛地用于定性预测各类ABn型分子的几何构型，解释键长和键角变化，偏离标准值的规律性，但也有少数化合物的推测出现例外.例如BaI2，SrCl2都是弯曲形构型而非预计的直线性型.此外，对过渡金属化合物几何构型的判断也有一定的局限性.实际上，应用价电子对互斥理论的分子体系，都有一个共同的特点，即分子中所有电子都是成对的.如果分子中有未成对的电子，则不能简单地以此方法来推测分子的几何构型.对于不具有半满或全满d轨道的过渡元素，由于d轨道上电子分布不对称，将使分子形状不规则化，无法用价电子对互斥理论作出判断，因而配位场理论则能说明得更好.价电子对互斥理论被看成是杂化轨道理论简化了的方法.而它相当于只考虑了中心原子利用杂化轨道成键后，各电子对之间的相互排斥，因而只能作出大致的定性说明.而杂化轨道理论则还考虑了整个的杂化过程，并可得出定量的结果，如计算键角等.。

分子结构

分子结构


H－N＝N＝N
H－N－N≡N
（3） 可以判断原子之间键长的长短 一般来说键级越大，键能越大，键长越短 在HN3中，N(a)－N(b) 的键长＞N(b)－N(c) 的键长 在C6H6中，C－C键的键长都是一样的，都可以通 过键级来判断。
6、Lewis八电子结构式的例外（Special conditions）
形式电荷与元素性质没有任何直接联系，它是共价 键形成的平等与否的标志。
（2） QF的计算公式：
QF = 原子的价电子数 键数 孤电子数 在CO中： QF(C) = 4 3 2 = 1 QF(O) = 6 3 2 = +1
0 0 0
H N N N
H N N N
2
H N N N
（二）共价键的类型
1、σ键 原子轨道沿键轴（两原子核间联线）方向以 “头碰头” 方式重叠所形成的共价键称为σ键。 形成σ键时，原子轨道的重叠部分对于键轴呈圆 柱形对称，沿键轴方向旋转任意角度，轨道的形 状和符号均不改变。
2、π键 原子轨道垂直于键轴以 “肩并肩” 方式重叠 所形成的共价化学键称为π键。形成π键时，原子 轨道的重叠部分对等地分布在包括键轴在内的平面 上、下两侧，形状相同，符号相反，呈镜面反对称。
Positive overlap
Negative overlap Zero overlap
σ bond
π bond
δ bond
综上所述，形成共价键的条件： (i) 要有单电子 (ii) 原子轨道能量相近 (iii) 电子云最大重叠 (iv) 必须相对于键轴具有相同对称性原子轨道（即 波函数角度分布图中的 +、+ 重叠， 、 重叠， 称为对称性一致的重叠）。
（1） 对于奇电子化合物，如NO、NO2等，只能用 特殊的方法表示：
分子结构与性质：分子的几何构型

分子结构与性质：分子的几何构型


3
S
F F
2
结论：LP占据水平方向三角形, 稳定 分子构型为变形四面体(跷跷板形)。
电子对的
VP LP 空间构型 5 1 三角双锥 5 2 三角双锥 5 3 三角双锥
分子的
例
空间构型
变形四方体 SF4
T形
ClF3
直线形
XeF2
进一步讨论影响键角的因素：
①π键的存在，相当于孤对电子排斥成
键电子，使键角变小。例如：
强，形成化学键的键能大，生成的分子 稳定。
由于成键原子轨道杂化后.轨道角度分布图的形状发生 了变化(一头大，一头小)，杂化轨道在某些方向上的角 度分布，比未杂化的P轨道和s轨道的角度分布大得多， 成键时从分布比较集中的一方(大的一头)与别的原子成 键轨道重叠，能得到更大程度的重叠，因而形成的化 学键比较牢固。
6-3-2 杂化轨道理论
为解决价键理论的局限性，鲍林在价键 理论中引入了杂化轨道的概念。
6-3-2 杂化轨道理论
杂化轨道理论的要点
原子成键时, 参与成键的若干个能级相近的原 子轨道相互“混杂”, 组成一组新轨道 (杂化 轨道),这一过程叫原子轨道的“杂化”。
杂化轨道理论的要点
有几个原子轨道参与杂化，就形成几个杂 化轨道 。 杂化轨道比原来未杂化的轨道成键能力
实例
22
例２BeCls2、(gp) 180° 直线形 σ键 直线形 BeCl2、CO2
Be
激发
sp杂化
2p 2s
2p 2s
sp 2p
能量近似原则 Cl—Be—Cl
Cl
Be
Cl
思考题：为什么不形成BeCl4分子？直线形
杂化类型
sp2杂化——１个s 轨道+2个p 轨道
判断几何构型

判断几何构型

实例分析：试判断H2O分子的空间构型。
解 ：O是H2O分子的中心原子，它有 6个价电子，与O化合的2个H原子各提供1个电子，所以O原子价层电子对数为（6+2）/2 = 4，其排布方式为 四面体，因价层电子对中有2对孤对电子，所以H2O分子的空间构型为V形。
精心搜集整理，只为你的需要
判断几何构型
价层电子对理论(VSEPR theory)预测分子空间构型步骤为：
1.确定中心原子中价层电子对数
中心原子的价层电子数和配体所提供的共用电子数的总和减去离子带电荷数除以2[价电子对数=1/2(中心原子的价电子数+配位原子提供的σ电子数-离子电荷代数值）]，即为中心原子的价层电子对数。 规定：(1)作为配体，卤素原子和H 原子提供1个电子，氧族元素的原子不提供电子；(2)作为中心原子，卤素原子按提供7个电子计算，氧族元素的原子按提供6个电子计算；(3)对于复杂离子，在计算价层电子对数时，还应加上负离子的电荷数或减去正离子的电荷数；(4)计算电子对数时，若剩余1个电子，亦当作 1对电子处理。(5的空间构型
根据中心原子的价层电子对数，从表9-4中找出相应的价层电子对构型后，再根据价层电子对中的孤对电子数，确定电子对的排布方式和分子的空间构型。
实例分析:试判断PCl5离子的空间构型。
解：P离子的正电荷数为5，中心原子P有5个价电子，Cl原子各提供1个电子，所以P原子的价层电子对数为（5+5-0）/2 = 5，其排布方式为三角双锥。因价层电子对中无孤对电子，所以PCl5 为三角双锥构型。
分子的空间构型

分子的空间构型


SP3杂化
由1个s轨道和3个p轨道混杂并重新组合成4个能量 与形状完全相同的轨道。由于每个轨道中都含有1/4 的s轨道成分和3/4的p轨道成分，因此我们把这种轨 道称之为 sp3杂化轨道。
为了四个杂化轨道在空间尽可能远离,使轨道间的排 斥最小,四个杂化轨道的伸展方向分别指向正四面体 的四个顶点.
种轨道称之为sp2杂化轨道。
sp2杂化轨道的形成和空间取向示意图
sp2杂化轨道的形成和特点：
由1个s轨道与2个p轨道组合成3个sp2 杂化轨
道的过程称为sp2 杂化。每个sp2 杂化轨道中含有1/3 的s轨道成分和2/3的p轨道成分。
为使轨道间的排斥能最小，3个sp2杂化轨道呈正 三角形分布，夹角为1200。当3个sp2杂化轨道分别与 其他3个相同原子的轨道重叠成键后，就会形成平面 三角形构型的分子。
SP 2 2 180° 直线形 BeCl2 CO2 HgCl2 [Ag(NH3)2]+
SP2 3 3 120° 平面三 角形 BF3 COCl2 NO3— CO32—
SP3 4 4 109.5° 四面体 CH4 CCl4 CHCl3 PO43— 三角 双锥 PCl5 八面体 SF6
价电子 对数目 杂化类 型 理想几 何构型
注：在化合物中以等电子观点看：O－ 和F、Cl、NH2相当，O和CH2、NH相当。 则：
NO2 NOCl NO3 NO2 Cl
1个O 换 成 1个Cl
-
1个O 换 成1个Cl
-
CO3 COCl2
CH 3CH 2 CH 3 CH 3OCH 3
第一单元
分子构型与物质的性质
一 分子的空间构型
分子的空间构型 三原子分子的空间构型有直线型和V型两种.如 CO2分子为直线型,而水的空间构型为V型,键角为 104.5°
键类型、分子构型、分子极性判断方法

键类型、分子构型、分子极性判断方法

对排布的几何构型主要决定于中心原子的价电子层中电子对的数目。所
谓价层电子对包括成键的σ电子对和孤电子对。价层电子对各自占据的
位置倾向于彼此分离得尽可能地远些，这样电子对彼此之间的排斥力最 小，整个分子最为稳定。这样也就决定了分子的空间结构。也正因此， 我们才可以用价层电子对很方便地判断分子的空间结构。例如：甲烷分 子（CH4），中心原子为碳原子，碳有4个价电子，4个氢原子各有一个 电子，这样在中心原子周围有8个电子，4个电子对，所以这4个电子对 互相排斥，为了使排斥力最小，分子最稳定，它们只能按正四面体的方 式排布。这样就决定了CH4的正四面体结构。
用，它们趋向于尽可能的相互远离。于是价层电子对的空间构型与价层
电子对数目的关系如下表所示：
这样已知价层电子对的数目，就可及确定它们的空间构型。 ③分子空间构型的确定。价层电子对有成键电子对和孤电子对之分。
中心原子周围配位原子（或原子团）数，就是健对数，价层电子对的总 数减去键对数，得孤对数。根据键对数和孤对敌，可以确定相应的较稳 定的分子几何构型，如下表所示：
而 SO32－离子却是呈三角锥体，硫是锥顶，三个氧原子是三个锥角，象 一架撑开的照相用的三角架。又例如SO2的三个原子不在一条直线上， 而CO2却是直线分子等等。价层电子对互斥理论用以预测简单分子或离 子的立体结构，我们不难学会用这种理论来预测和理解分子或离子的立
体结构，并用来进一步确定分子或离子的结构。 价层电子对互斥理论认为，在一个共价分子中，中心原子周围电子
成
电
孤
电子 键
子
电
对的 电
对
子
空间 子
数
对
构型 对
目
数
数
电子对的 排列方式
分子的 空间构 实 例

判断分子空间几何构型的简单方法

判断分子空间几何构型的简单方法以下用G表示电子对数目,V表示分子中所有原子最外层电子数的与,n表示配位原子中除了氢原子以外的其它原子的个数,m表示孤电子对数目,r表示配位原子中氢原子的个数。

当配位原子中没有氢原子且V≥16时:V=8n＋2m,G=m＋n 例:CO2分子构型的判断V=4＋6×2=8n＋2m,这里n=2,∴m=0,∴G=m＋n=0＋2=2,所以CO2的分子构型为直线型BF3分子构型的判断V=3＋7×3=8n＋2m,这里n=3,∴m=0,∴G=m＋n=0＋3=3,所以BF3的分子构型为三角形PCl5分子构型的判断V=5＋7×5=8n＋2m,这里n=5,∴m=0,∴G=m＋n=0＋5=5,所以PCl5的分子构型为三角双锥SF4分子构型的判断V=6＋7×4=8n＋2m,这里n=4,∴m=1,∴G=m＋n=1＋4=5,所以SF4的分子构型为变形四面体BrF3分子构型的判断V=7＋7×3=8n＋2m,这里n=3,∴m=2,∴G=m＋n=2＋3=5,所以BrF3的分子构型为T型SF6分子构型的判断V=6＋7×6=8n＋2m,这里n=6,∴m=0,∴G=m＋n=0＋6=6,所以SF6的分子构型为八面体XeF4分子构型的判断V=8＋7×4=8n＋2m,这里n=4,∴m=2,∴G=m＋n=2＋4=6,所以XeF4的分子构型为正方形当配位原子中有氢原子且V＜16时:V=2r＋8n＋2m, G=m＋n＋r。

例:CH4分子构型的判断V=4＋1×4=2r＋8n＋2m,这里r=4,n=0,∴m=0, ∴G=m＋n＋r=0＋0＋4=4,所以CH4的分子构型为四面体NH3分子构型的判断V=5＋1×3=2r＋8n＋2m,这里r=3,n=0,∴m=1,∴G=m＋n＋r=1＋0＋3=4,所以NH3的分子构型为三角锥 H2O分子构型的判断V=6＋1×2=2r＋8n＋2m,这里r=2,n=0,∴m=2,∴G=m＋n＋r=2＋0＋2=4,所以H2O的分子构型为V型HClO分子构型的判断V=1＋7＋6=2r＋8n＋2m,这里r=1,n=1,∴m=2,∴G=m＋n＋r=2＋1＋1=4,所以HClO的分子构型为V型HNO分子构型的判断V=1＋5＋6=2r＋8n＋2m,这里r=1,n=1,∴m=1,∴G=m＋n＋r=1＋1＋1=3,所以HNO的分子构型为V型HCN分子构型的判断V=1＋4＋5=2r＋8n＋2m,这里r=1,n=1,∴m=0,∴G=m＋n＋r=0＋1＋1=2,所以HCN的分子构型为直线型注:以上所介绍的方法只有当V为偶数时才适用,当V为奇数时,只需将V与G瞧成比它们大1的偶数即可！。

化学键和分子结构几个问题的讨论

知识探究： 化学键和分子结构Chemical Bonds and Structures of Molecules这一章是化学的核心，因为结构决定性质。

如白磷、红磷的结构不同，性质也不同；石墨、金刚石和C 60等的结构不同，性质也不同。

这一章重点讲授共价键、离子键、金属键以及分子几何构型、金属晶体、原子晶体和离子晶体的晶体结构。

另外我们也讨论分子间的作用力以及对分子晶体的一些性质的影响。

共价键与分子几何构型Covalent Bonds and Molecular Geometric Structure*（要求了解）一、经典共价键理论（Classical Covalent Bond Theory ） − LewisStructure (Octet Rule)（八电子规则）1．基本思想：当n s 、n p 原子轨道充满电子，会成为八电子构型，该电子构型是稳定的，所以在共价分子中，每个原子都希望成为八电子构型（H 原子为2电子构型）。

2．共价分子中成键数和孤电子对数的计算：例如：P 4S 3、HN 3、N +5、H 2CN 2（重氮甲烷）、NO -3 (1) 计算步骤：a ．令n o − 共价分子中，所有原子形成八电子构型（H 为2电子构型）所需要的电子总数b ．令n v − 共价分子中，所有原子的价电子数总和c ．令n s − 共价分子中，所有原子之间共享电子总数 n s = n o - n v ，n s /2 = (n o - n v ) / 2 = 成键电子对数d ．令n l − 共价分子中，存在的孤电子数。

（或称未成键电子数）3．Lewis 结构式的书写P 4S 3HN 3HN N N H N N HNNNN 5+，，，N N NNNNNN NNNNNN N N NCH 2N 2（重氮甲烷） ，HCHNN HC HN N当Lewis 结构式不只一种形式时，如何来判断这些Lewis 结构式的稳定性呢？如HN 3可以写出三种可能的Lewis 结构式，5N +可以写出四种可能的Lewis 结构式，而重氮甲烷只能写出两种可能的Lewis 结构式。

判断分子空间几何构型的简单方法

判断分子空间几何构型的简单方法以下用G表示电子对数目，V表示分子中所有原子最外层电子数的和，n表示配位原子中除了氢原子以外的其它原子的个数，m表示孤电子对数目，r表示配位原子中氢原子的个数。

当配位原子中没有氢原子且V≥16时：V=8n＋2m，G=m＋n 例：CO2分子构型的判断V=4＋6×2=8n＋2m，这里n=2，∴m=0,∴G=m＋n=0＋2=2，所以CO2的分子构型为直线型BF3分子构型的判断V=3＋7×3=8n＋2m，这里n=3，∴m=0,∴G=m＋n=0＋3=3，所以BF3的分子构型为三角形PCl5分子构型的判断V=5＋7×5=8n＋2m，这里n=5，∴m=0,∴G=m＋n=0＋5=5，所以PCl5的分子构型为三角双锥SF4分子构型的判断V=6＋7×4=8n＋2m，这里n=4，∴m=1,∴G=m＋n=1＋4=5，所以SF4的分子构型为变形四面体BrF3分子构型的判断V=7＋7×3=8n＋2m，这里n=3，∴m=2,∴G=m＋n=2＋3=5，所以BrF3的分子构型为T型SF6分子构型的判断V=6＋7×6=8n＋2m，这里n=6，∴m=0,∴G=m＋n=0＋6=6，所以SF6的分子构型为八面体XeF4分子构型的判断V=8＋7×4=8n＋2m，这里n=4，∴m=2,∴G=m＋n=2＋4=6，所以XeF4的分子构型为正方形当配位原子中有氢原子且V＜16时：V=2r＋8n＋2m， G=m＋n＋r。

例：CH4分子构型的判断V=4＋1×4=2r＋8n＋2m，这里r=4，n=0，∴m=0，∴G=m＋n＋r=0＋0＋4=4，所以CH4的分子构型为四面体NH3分子构型的判断V=5＋1×3=2r＋8n＋2m，这里r=3，n=0，∴m=1，∴G=m＋n＋r=1＋0＋3=4，所以NH3的分子构型为三角锥 H2O分子构型的判断V=6＋1×2=2r＋8n＋2m，这里r=2，n=0，∴m=2，∴G=m＋n＋r=2＋0＋2=4，所以H2O的分子构型为V型HClO分子构型的判断V=1＋7＋6=2r＋8n＋2m，这里r=1，n=1，∴m=2，∴G=m＋n＋r=2＋1＋1=4，所以HClO的分子构型为V型HNO分子构型的判断V=1＋5＋6=2r＋8n＋2m，这里r=1，n=1，∴m=1，∴G=m＋n＋r=1＋1＋1=3，所以HNO的分子构型为V型HCN分子构型的判断V=1＋4＋5=2r＋8n＋2m，这里r=1，n=1，∴m=0，∴G=m＋n＋r=0＋1＋1=2，所以HCN的分子构型为直线型注：以上所介绍的方法只有当V为偶数时才适用，当V 为奇数时，只需将V和G看成比它们大1的偶数即可！。

分子几何构型公式

分子几何构型公式
分子几何构型公式是一种描述分子三维结构的表示方法。

它使用原子之间的连接关系以及电子对的排布来确定分子的形状。

以下是一些常见的分子几何构型及其相应的公式：
1. 线性（Linear）：M-A-B，其中 M 为中心原子，A 和 B 是两个连接在 M 上的原子。

例子：CO₂
2. 角形（Trigonal Planar）：M-A-B-C，其中 M 为中心原子，
A、B、C 是连接在 M 上的原子。

例子：BF₃
3. 四面体（Tetrahedral）：M-A-B-C-D，其中 M 为中心原子，
A、B、C、D 是连接在 M 上的原子。

例子：CH₄
4. 三角双锥（Trigonal Bipyramidal）：M-A-B-C-D-E，其中 M 为中心原子，A、B、C、D、E 是连接在 M 上的原子。

例子：PCl₅
5. 八面体（Octahedral）：M-A-B-C-D-E-F，其中 M 为中心原子，A、B、C、D、E、F 是连接在 M 上的原子。

例子：SF₆
这些是常见的几种分子几何构型，每种构型都有对应的原子连接关系和电子排布方式。

请注意，这些公式表示的是分子的理想化结构，实际分子的构型可能受到原子间的电子云排斥、键角扭曲等因素的影响而发生变化。

判断分子空间几何构型的简单方法

判断分子空间几何构型的简单方法
分子空间几何的构型是研究分子的化学性质和关联性质的重要参考，由此可以知道物质的密度、电荷密度分布特征和电子激发态的迁移以及分子的位移和变形，从而能够更好的预测分子的后续反应特性。

在实际的研究过程中，如何判断分子空间几何构型，是一个关于分子结构与功能之间关系的重要步骤。

最常用的方法是通过实验观察，采用X射线衍射或NMR技术，对分子中的原子进行测看和定位，获取分子空间几何构型的具体信息，从而判断该物质的构型模式。

但是，随着科技的发展，计算机模拟技术也在不断完善，它将实验所需的大量重复工作，转化为电脑的模拟运算，从而使得对分子构型的判断非常简单。

另一种常用的方法是对分子的构型进行理论推演，根据分子中所包含的原子及其电子表象力、共价键角以及化学键长等特征，以某种特定斥力场下的极限决定方程来预测分子的几何构型、结构和性质，从而进行判断。

而这种方法的优势在于可以较为直观的得到分子的轨道构型，而对于复杂的分子构型来说也是一种很直接的判断方法。

综上所述，判断分子空间几何构型的简单方法有实验观察和计算理论推演两种。

实验观察可以采用X射线衍射或NMR技术，而理论推演则是根据分子中所包含的原子及其相关特征，利用某种特定斥力场下的极限决定方程来判断分子的构型。

虽然这两种方法都能够较快得到预期结果，但在实际中，如何根据判断出来的结果应用到研究中还需要仔细结合该分子特性深入思考。

if3中i的几何构型

if3中i的几何构型在化学中，分子的几何构型对于分子的性质和反应具有重要影响。

if3是一种分子式为IF3的化合物，其中包含一个氟原子和三个碘原子。

本文将探讨if3中i的几何构型及其相关性质。

if3分子的结构if3是一种由一个氟原子和三个碘原子组成的分子。

根据VSEPR理论（Valence Shell Electron Pair Repulsion，价壳层电子对斥力理论），分子中的电子对会互相排斥，力求使其间距最大化。

根据这一理论，我们可以推测if3分子的几何构型。

VSEPR理论VSEPR理论基于以下假设：1.原子之间和孤立电子对之间的排斥力相等。

2.电荷密度越高，排斥力越强。

3.具有相同数目的电荷密度（双键或孤立电子对）之间的排斥力相等。

根据这些假设，我们可以预测if3分子中i原子周围电荷密度最低，并且与其他原子之间存在最小排斥力。

if3中i原子的几何构型根据上述推理，我们可以得出if3分子中i原子的几何构型为三角双锥形。

在这种构型中，i原子位于一个平面上，三个碘原子则位于该平面之外。

if3分子的性质if3分子的几何构型对于其性质具有重要影响。

下面将介绍if3分子的一些性质。

极性由于if3分子中包含一个氟原子和三个碘原子，而氟原子比碘原子更电负，因此if3分子是极性分子。

在三角双锥形几何构型中，氟原子位于平面上方，而碘原子则位于平面之外。

这种不均匀的电荷分布导致了分子整体呈现极性。

反应性if3分子由于其极性和几何构型的特殊性质，在化学反应中表现出一定的特异性。

例如，在与其他化合物发生反应时，if3可以作为路易斯酸（电荷亲合剂）与路易斯碱（电荷供体）发生相互作用。

此外，由于if3分子中i原子周围存在较高的电荷密度，它也可能参与其他相互作用或反应。

用途if3分子在化学领域具有一定的用途。

例如，它可用作催化剂，在某些有机合成反应中发挥重要作用。

此外，if3也可用于其他研究领域，如材料科学和表面化学等。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、 轨道杂化理论 ( Pauling, 1931) Hybridization Theory
1、轨道的杂化 、 在同一个原子中能量相近的不同类型的几 个原子轨道在成键时可以相互叠加而组成同等 个原子轨道在成键时可以相互叠加而组成同等 数量的能量完全相同的杂化原子轨道 数量的能量完全相同的杂化原子轨道 原子形成杂化轨道的一般过程 激发 杂化 轨道重叠
• 孤对电子相对来说带有较多的负电荷。受孤 孤对电子相对来说带有较多的负电荷。 对电子云的排斥， 分子中N－ 键间的夹 对电子云的排斥，NH3分子中 －H键间的夹 角被压缩为107º，H2O分子中 分子中O—H键间的夹 角被压缩为 ， 分子中 键间的夹 角被压缩到104º40¹。 角被压缩到 。 • 含有孤对电子的杂化被称为不等性杂化。 含有孤对电子的杂化被称为不等性杂化。 不等性杂化 NH3和H2O分子中 和O都发生了不等性 3杂 分子中N和 都发生了不等性 都发生了不等性sp 分子中 化
• 四个 3 杂化轨道在空间均匀对称地分布 四个sp 杂化轨道在空间均匀对称地分布— —以碳原子核为中心，伸向正四面体的四个 以碳原子核为中心， 以碳原子核为中心 顶点。 顶点。这四个杂化轨道的未成对电子分别与 氢原子的1s电子配对成键 电子配对成键， 氢原子的 电子配对成键，这就形成了甲烷 分子。 分子。
②sp2杂化
分子时， • 碳原子在形成乙烯（C2H4）分子时，每个碳原 碳原子在形成乙烯（ 子的2S轨道与两个 轨道发生杂化，称为sp 轨道与两个2p轨道发生杂化 子的 轨道与两个 轨道发生杂化，称为 2杂 杂化后形成3个杂化轨道 它们的形状与sp 个杂化轨道。 化。杂化后形成 个杂化轨道。它们的形状与 3 杂化轨道相似， 杂化轨道相似，在空间以碳原子梭为中心指向平 面正三角形的三个顶点。 面正三角形的三个顶点。 • 未杂化的 个2p轨道则垂直于杂化轨道所在的平 未杂化的l个 轨道则垂直于杂化轨道所在的平 面。3个sp2杂化轨道与未杂化的 1个2p轨道各有 个 个 轨道各有 1个未成对电子。两个碳原子分别以 个sp2杂化 个未成对电子。 个未成对电子 两个碳原子分别以1个 轨道互相重叠形成σ 两个碳原子的另外4个 轨道互相重叠形成σ键，两个碳原子的另外 个 sp2杂化轨道分别与氢原子结合。 杂化轨道分别与氢原子结合。
•
• 碳原子在形成乙炔（C2H2）时也发生 碳原子在形成乙炔（ 时也发生sp 杂化，两个碳原子以sp杂化轨道与氢原 杂化 ， 两个碳原子以 杂化轨道与氢原 子结合。 两个碳原子的未杂化2p轨道分 子结合 。 两个碳原子的未杂化 轨道分 别在Y轴和 轴方向重叠形成π键 轴和Z轴方向重叠形成 别在 轴和 轴方向重叠形成 键 。 所以 乙炔分子中碳原子间以叁挺相结合。 乙炔分子中碳原子间以叁挺相结合。
•
杂化轨道理论不仅说明了碳原子最外层虽 然只有2个未成对电子却可以与 个未成对电子却可以与4个氢原子形 然只有 个未成对电子却可以与 个氢原子形 成共价键， 成共价键，而且很好地说明了甲烷分子的正 四面体结构。 四面体结构。
• 在形成 2O、NH3分子时，O、N原子实际上 在形成H 、 分子时， 、 原子实际上 也发生了sp 杂化。 原子杂化不同的是N、 也发生了 3杂化。与C原子杂化不同的是 、 原子杂化不同的是 O原子最外层电子数分别为 个和 个，因而 原子最外层电子数分别为5个和 原子最外层电子数分别为 个和6个 四个sp 杂化轨道里必然分别有1个和 个和2个轨 四个 3 杂化轨道里必然分别有 个和 个轨 道排布了两个电子。 道排布了两个电子。这种已经自配对的电子 被称为孤对电子。 和 的未成对电子分别 被称为孤对电子 。 N和 O的未成对电子分别 原子的1s电子结合就形成了 与 H原子的 电子结合就形成了 3 分子和 原子的 电子结合就形成了NH H2O分子。 分子。 分子
3d杂化 ④sp 杂化
分子时，除最外层s、 轨 • 磷原子在形成 磷原子在形成PCl5分子时，除最外层 、p轨 道参与杂化外， 轨道也有1个参加了杂 道参与杂化外 ， 其 3d轨道也有 个参加了杂 轨道也有 称为sp 杂化 杂化。 化，称为 3d杂化。 • 杂化后形成 个杂化轨道， 杂化后形成5个杂化轨道 个杂化轨道， 其中各有1个未成对电子 个未成对电子。 其中各有 个未成对电子。 5个杂化轨道指向三角双锥 个杂化轨道指向三角双锥 个顶点， 的5个顶点，并与氯原子配 个顶点 对成键。 对成键。 • 除以上杂化方式外 ， 还有其它的杂化 ， 这里 除以上杂化方式外，还有其它的杂化， 从略。 从略。
(2) 等性杂化和不等性杂化 等性杂化： 等性杂化：参与杂化的原子轨道均为具有不 成对电子的轨道 不等性杂化： 不等性杂化：参与杂化的原子轨道不仅包含不 成对电子的轨道， 成对电子的轨道，也包含成对电子 的轨道。 的轨道。如NH3分子中的杂化轨道 孤对电子占有的杂化轨道不参与成 键作用 N ( 1s22s22px12py12pz1 ) 4个sp3 轨道 H2O
2、共价键的类型： 、共价键的类型： (1) σ键和 键 键和π键 键和 σ键 ：成键的两原子以“头碰头”的方式，沿 键 成键的两原子以“头碰头”的方式， 两原子核连线方向发生轨道重叠。 两原子核连线方向发生轨道重叠。
π键 ：成键时两原子轨道以“肩并肩”的方式 键 成键时两原子轨道以“肩并肩” 发生重叠，重叠部分对通过键轴、 发生重叠，重叠部分对通过键轴、密 度为零的一个平面呈对称分布
• 可以看出，杂化方式与分子的空间结构形状有关。一般 可以看出，杂化方式与分子的空间结构形状有关。 地说， 发生sp 杂化时， 形成的分子是正四面体， 地说 ， 发生 sp3 杂化时 ， 形成的分子是正四面体 ， 杂化 原子处于中心； 原子处于中心； • 发生不等性 sp3 杂化时 ， 如有一对孤对电子 ， 则分子呈 发生不等性sp 杂化时， 如有一对孤对电子， 三角锥形，杂化原子处于锥顶。如果有2对孤对电子， 三角锥形 ， 杂化原子处于锥顶 。 如果有 2 对孤对电子 ， 则分子呈V 则分子呈V型； • 发生 sp2 杂化时 ， 分子呈平面三角型 ， 杂化原子处于正 发生sp 杂化时， 分子呈平面三角型， 三角形中心， 未杂化的p 电子通常形成π 三角形中心 ， 未杂化的 p 电子通常形成 π 键 （ 构成双 键）； • 发生 sp 杂化时 ， 分子呈直线型 ， 未杂化的 p 电子通常也 发生sp杂化时，分子呈直线型，未杂化的p sp杂化时 参与形成π 构成双键或叁键） 参与形成π键（构成双键或叁键）； • 发生sp3d杂化时，分子是三角双锥形。杂化原子处于双 发生sp 杂化时，分子是三角双锥形。 三角雄的中心。 三角雄的中心。
两个原子的原子 核的连线称为键 键 轴。
一般说来，π键的重叠程度小于 σ键，所以π键的键能比σ键的பைடு நூலகம்键能小，更易于发生化学反应。
(2) 正常共价键和配位共价键 正常共价键：共用电子对由成键的两个原子 正常共价键： 共同提供。 共同提供。 配位共价键： 配位共价键：共用电子对由成键原子中的一个 原子提供 H H N : + H+ H H H N H H
• 所有碳原子和氢原子处于同一平面上，而两 所有碳原子和氢原子处于同一平面上， 个碳原子未杂化的2p轨道垂直于这个平面 轨道垂直于这个平面。 个碳原子未杂化的 轨道垂直于这个平面。 它们互相平行，彼此肩并肩重叠形成π 它们互相平行，彼此肩并肩重叠形成π键。 所以，在乙烯分子中两个碳原子是以双键相 所以， 结合，双键由一个σ和一个π键构成。 结合，双键由一个σ和一个π键构成。
①形成分子时，由于原子间的相互作用，使同 形成分子时，由于原子间的相互作用， 一原子中能量相近的不同类型原子轨道， 一原子中能量相近的不同类型原子轨道，例如 ns轨道与 轨道，发生混合，重新组合为一 轨道与np轨道 轨道与 轨道，发生混合， 组新轨道．称为杂化轨道。如一个2s轨道与三 组新轨道．称为杂化轨道。如一个 轨道与三 轨道混合， 个2p轨道混合，可组合成四个 3杂化轨道； 轨道混合 可组合成四个sp 杂化轨道； 一个2s轨道与二个 轨道混合，可得三个sp 轨道与二个2p轨道混合 一个 轨道与二个 轨道混合，可得三个 2 杂化轨道；一个2s轨道与一个 轨道混合， 轨道与一个2p轨道混合 杂化轨道；一个 轨道与一个 轨道混合， 可得二个sp杂化轨道 杂化轨道。 可得二个 杂化轨道。
CH4分子的形成 激发 2s 2p 2s 2p
杂化 Sp3 杂化轨道
成键 + 4H CH4分子
杂化
成键
• ①sp3杂化 杂化——碳原子在与氢原子形成甲烷分子 碳原子在与氢原子形成甲烷分子 时就发生了sp 杂化。发生杂化时， 时就发生了 3 杂化 。 发生杂化时 ， 碳原子的一 轨道和3个 轨道发生混杂 形成4个能量 轨道发生混杂， 个 2s轨道和 个 2p轨道发生混杂 ， 形成 个能量 轨道和 相等的杂化轨道，碳原子最外层的4个电子分别 相等的杂化轨道 ，碳原子最外层的 个电子分别 占据1个杂化轨道 个杂化轨道。 占据 个杂化轨道。 • 每一个 3杂化轨道的能量高于 轨道能量而低 每一个sp 杂化轨道的能量高于2s轨道能量而低 轨道能量； 于2p轨道能量；杂化轨道的形状也可以说介于 轨道能量 杂化轨道的形状也可以说介于s 轨道和p轨道之间 轨道之间。 轨道和 轨道之间。
• 此外，BF3分子中的 原子，SO3分子中的 此外， 分子中的B原子 原子， 分子中的S 原子都是发生sp 杂化的。 原子都是发生 2 杂化的 。 这些分子都呈平 面三角形。 面三角形。
③sp杂化 杂化
• 形成 形成CO2分子时，碳原子 个2s轨道与 个2p 分子时，碳原子1个 轨道与 轨道与1个 轨道发生杂化，形成两个sp杂化轨道 杂化轨道。 轨道发生杂化，形成两个 杂化轨道。两个 sp杂化轨道在 轴方向上呈直线排列，未杂化 杂化轨道在X轴方向上呈直线排列 杂化轨道在 轴方向上呈直线排列， 的两个即轨道分别在Y轴方向和 轴方向和Z铀方向垂直 的两个即轨道分别在 轴方向和 铀方向垂直 于杂化轨道。 于杂化轨道。 • 两个氧原子各以一个 轨道与碳原子的 杂 两个氧原子各以一个2p轨道与碳原子的 轨道与碳原子的sp杂 化轨道重叠形成σ 化轨道重叠形成σ键。而两个氧原子的另一个 未配对的2p轨道分别在 轨道分别在Y周 轴方向和Z轴方向 未配对的 轨道分别在 周 轴方向和 轴方向 与碳原子的未杂化的2p轨道 肩并肩” 轨道“ 与碳原子的未杂化的 轨道“肩并肩”重叠 形成π 所以CO2分子中碳、氧之间以双键 分子中碳、 形成π键。所以 相结合。 相结合。