2017年第十六届二升三学而思综合素质测评.数学解析

2016-2017年小升初数学试卷含答案解析往往是对基础知识的一种提升，基础知识没掌握好，会很容易失分，为此店铺准备了2016-2017年小升初数学试卷含答案解析，希望对你有所帮助!1. 有9名同学进羽毛球比赛，任意两名同学都进行一场比赛，共进行了_________场比赛。

2. 一个三位小数用四舍五入法取近似值是8.30，这个数原来最大是_________.3. 某校开展评选“优秀少先队员”和“好公民”活动，“好公民”占评上人数的，“优秀少先队员”占评上人数的，同时获得两种称号的有44人，只获得“优秀少先队员”称号的有_________人。

4. 在一个减法算式中，差与减数的比是3:5，减数是被减数的_________%。

5. 一台收音机原价100元，先提价10%，又降价10%，现在售价是_________元。

6. 一个长方形与一个正方形的周长相等，长方形的长与宽的比是5:3，已知正方形的面积是4平方厘米，则长方形的面积是_____________。

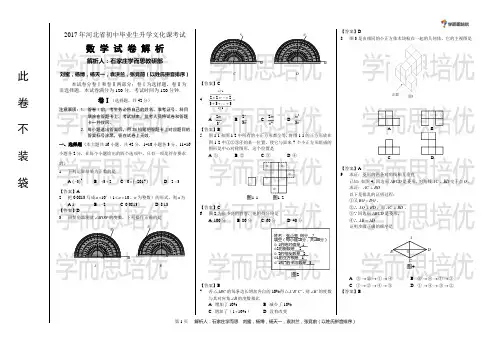
7. 如图，在棱长为3的正方形中由上到下，由左到右，有前到后，有三个底面积是1的正方形高为3的长方体的洞，则该几何体的表面积为_________。

(7题图) (10题图)8. 一种杂志，批发商按定价打七折批发給书摊，摊主将原定价格降10%卖给读者，如果这种杂志每本卖7.2元，每卖出一本摊主从中赢利_________元9. △+△=a, △—△=b, △×△=c，△÷△=d, a+b+c+d=100,那么△_________。

10. 将正整数1,2,3,4……按箭头所指的方向排列(如图)，在2,3,5,7,10……等位置转弯，则第50次转弯处的数是___________.得分二、选择题：(每小题2分，共20分)二、选择题：(每小题2分，共20分)11.如果用□表示一个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么右图由7个立方体叠加的几何体，从正面观察，可画出的平面图形是( )A. B. C. D.12. 投掷3次硬币，有2次正面朝上，1次反面朝上，那么投掷第4次反面朝上的可能性是( )A.1B.C.D.13.一个长方体的长、宽、高分别是a米、b米和h米，如果高增加4米，体积增加( )A.4bhB.4abhC.4abD.ab(h+4)14.有五根木条，他们的长度分别是1厘米，2厘米，3厘米，4厘米，5厘米，从他们当中选3根木条拼成一个三角形，一共可以拼成( )三角形。

绝密★启用前2017年秋季北京市小学生综合能力测评暨计算大比拼二年级数学试卷考试时间：60分钟满分：200分考生须知：请将所有的答案写在答题纸．．．对应横线上一、基础过关（每题8分，共40分）++++++++=________.1.123454321÷÷⨯⨯=________.2.4868233.比较图1和图2中的空白部分大小，图________空白部分所占的地方更大一些.图1图24.下面的线条图形中，只有．．一幅图可以一笔画出，这幅图是_____（请填入A/B/C/D）.5.下图是用火柴棒摆出的0~9共10个数字，用5根火柴棒能摆出的最大的数是______.二、思维拓展（每题10分，共50分）6.玲珑塔，塔玲珑，玲珑宝塔有7层，一层一桌4条腿，还有1个和尚点着灯；二层两桌8条腿，也是1个和尚点着灯；三层三桌12条腿，还是1个和尚来点灯；这个规律往下排，问玲珑塔中，桌腿和人腿共有______条.DCBA7.请根据你找到的规律，补全下方九宫格，并将正确图形的选项填入横线中，正确的图形是______（请填入A/B/C/D）.A B C D8.如果1个平底锅煎鸡蛋，每次最多能放2个鸡蛋，煎熟1个鸡蛋需要用时2分钟（正反面各需要1分钟）.同时用2个平底锅煎熟7个鸡蛋至少需要________分钟.9.找出数列的规律，在横线上填上正确的数：199,123,76,47,______,18,11,7,4,3.10.数一数下面这个小鸟图片里包含了_____个三角形.三、超常挑战（每题12分，共60分）11.下图是中国的“中”字，有________种方法可以将它一笔画出.12.有一张披萨被切成若干块，艾迪来了吃了一半多6块；减减来了吃了剩下部分的一半少6块；薇儿带来了和剩余披萨一样多的块数，还多6块，现在共有66块，那么这张披萨原来有________块.13.将“＋,－,×,÷”四个符号各一个填入合适的地方，使算式结果最大，那么算式结果最大是________.2017123＝（如20－1＋7÷1×23=20－1+7÷1×23=19＋7×23=19＋161=180）14.如图有一个五环广场，在下图每个黑点处原来各有1棵树.然后薇儿沿着5个圆环的边缘继续种树，每个圆环的长度是40米，最终每个圆环上的树的间隔是4米，那么薇儿又种了________棵树.15.薇儿从商店里买了一盒铅笔，里面只有红色和黄色的铅笔.薇儿打开盒子数了数发现：如果用这盒铅笔的总数加上其中红色铅笔的数量，那么和为18；如果这盒铅笔的总数加上其中黄色铅笔的数量，那么和为12．请问，这盒铅笔有________支.四、智力谜题（第16、17题每题15分，第18题20分，共50分）16.规则：在空格内填入数字1-5，使得每行、每列和4个凹形粗线框内数字都不重复.那么从上往下数第3行的数字依次是__________.17.规则：下面是一个立体方格数独，在每个方格里填入数字1,2,3,4,使得每个箭头方向的4个格内均有数字且数字不重复.那么红框处应填的数字是________.18.有1张足够长的长方形纸条，纸条的一面是黑色，另一面是红色；如果用1张纸条折出红、黑相间的“十”字图案，则折成“十”字图案最少需要折__________次（折纸之间允许叠加,多余部分和小的缝隙不用考虑）.。

启用前★绝密2017年第七届南京学而思综合能力䈀ᯣ数学（二年级）考试时间：60分钟满分：200分考生须知：请将所有的答案写在答题纸．．．对应位置上一、基础过关（每题8分，共40分）1.计算：（1）1＋4＋7＋10＋13＋16＋19= ▲．（2）96－（56＋19）= ▲．2.春天到啦，薇儿要出去郊游，她想要选择一条裙子和一双鞋子．薇儿一共有三条裙子，两双鞋子．薇儿一共有▲种不同的搭配方法．3.武西要看一本书，第一天看了这本书的一半，第二天看了剩下部分的一半，第三天看了8页，还剩5页没有看完，这本书一共有▲页．4.悟空招来他的猴子猴孙，4只小猴分一组，分了4组还剩3只小猴．聪明的小朋友，算一算，悟空招来了▲只小猴子．5.图中有红桃3，方片6和梅花10，请你再摆上一张黑桃牌，让黑色牌的点数之和是红色牌点数之和的2倍，你会放上黑桃▲．红桃3 方片6 梅花10 黑桃？二、思维训练（每题10分，共50分）6.25个小朋友排队，从左往右数艾迪是第12个，从右往左数薇儿是第9个，艾迪和薇儿之间有▲个小朋友．7.下面的线条图形中，只有一幅图可以一笔画出，这幅图是▲．（请填入A、B、C或D）A B C D8.4月1日是愚人节，今年的愚人节是星期六．现在有写着数字4、1、6的三张卡片，则共可以组成▲个不同的三位数．（6可以旋转变成9）9.一只鸡有1个头2条腿，一只兔子有1个头4条腿．如果笼子里的鸡和兔子共有10个头和26条腿，那么鸡有▲只，兔有▲只．10.艾迪寒假的时候去海边度假，穿着当地特色的衣服，拍了照片．现在我们一起来数一数，照片里一共．．可以数出▲个三角形．三、 思维拓展（每题10分，共50分）11. X 别动队队员找到个藏宝屋，发现藏宝屋的门锁是一个密码锁（如下图所示），其中的数是按照一定规律排列的，请按照你找到的规律，将正确的数填入空格内，这个数是 ▲ ．12. 我国的农历用“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”这十二种动物按顺序轮流代表各年的年号．例如，第一年如果是鼠年，那第二年就是牛年，第三年就是虎年，……如果从某年往后数的第1年是鸡年，那么第120年是 ▲ 年．13. 乘乘用四个相同的长方形和一个小正方形组成一个大正方形，每个长方形的周长为10厘米，大正方形的周长为 ▲ 厘米．14. 艾迪排在一个十字形队伍的正中间，这个队伍一共有27人，横排人数是竖排人数的 3 倍，那么横排有 ▲ 人．15. 薇儿一共有22张积分卡，平均分给了一些小朋友，最后还剩4张无法继续分，那么小朋友的人数有 ▲ 种可能．四ǃ挑战（每题12分，共60分）16. 有一个如图所示形状的花坛，艾迪要绕着这个花坛摆花盆，每隔2米摆一盆，一共要摆 ▲ 盆花．（图中单位均为米）17. 将1、2、3、4、5、6这6个数字分别填入下面的“” 中，使得下面的一句话成立．其中有一个中的数字已经填好．这句话是这样的：玲玲非常喜欢做《计算天天练》，每做完一页需要18分钟，玲玲从开始做，做完一页后正好是．18. 在空格中填入数字1-4，使得每行、每列和每个粗线框内数字都不重复．格里的小数表示这个格的上下左右四个格中有多少个比它大的数字．图中B 代表的数是 ▲ ．64101019.有4张卡片，每张卡片上各写着一个互不相同的数字．博士首先将这4张卡片发给大毛、二毛、三毛和四毛四个小朋友，然后收回来再分别发给四人各一张，如此一共发了3次．如果把3次收到的卡片上的数字相加，大毛的和是0，二毛的和是3，三毛的和是11，四毛的和是16．请问这四张卡片上最大的数字是▲．20.下图给出了用火柴棍摆数字0～9 的方法．（1）现有9根火柴棍，要求全用完，则能摆出最小．．的两位数是▲．（2）现有20根火柴棍，要求全用完，则能摆出最小．．的数是▲．2017年第七届南京学而思综合能力诊断（答题纸）数学(二年级)总分：200分考试时间：2017年4月4日8:30 - 9:30准考证号（请用2B铅笔填涂下方的考号）姓名17请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效启用前★绝密2017年第七届南京学而思综合能力诊断数学（二年级）考试时间：60分钟满分：200分考生须知：请将所有的答案写在答题纸．．．对应位置上一、 基础过关（每题8分，共40分） 1. 计算：（1）1＋4＋7＋10＋13＋16＋19= ▲ ． （2）96－（56＋19）= ▲ ．【解析】（1）等差数列求和，个数为奇数，和=中间数×个数，10×7=70 （2）去括号，96－56－19=21 【答案】70；212. 春天到啦，薇儿要出去郊游，她想要选择一条裙子和一双鞋子．薇儿一共有三条裙子，两双鞋子．仔细想一想，薇儿一共有 ▲ 种搭配方法． 【解析】三条裙子可分别标记为A 、B 、C ，两双鞋子可分别标记为1、2．所有搭配为：A 1、A 2、B 1、B 2、C 1、C 2，共6种． 【答案】63. 武西要看一本书，第一天看了这本书的一半，第二天看了剩下部分的一半，第三天看了8页，还剩5页没有看完，这本书一共有 ▲ 页． 【解析】逆向思考，画流程图【答案】524. 悟空招来他的猴子猴孙，4只小猴分一组，分了4组还剩3只小猴．聪明的小朋友，算一算，悟空招来了 ▲ 只小猴子．()()()5132652822−→−−→−−→−÷÷－【解析】4×4＋3=19（只）．【答案】195.图中有红桃3，方片6和梅花10，请你再摆上一张黑桃牌，让黑色牌的点数之和是红色牌点数之和的2倍，你会放上黑桃▲．【解析】红色扑克牌点数和为3＋6=9，那么黑色扑克牌点数和为9×2=18，还需放上的黑桃牌点数为18－10=8．【答案】8二、思维训练（每题10分，共50分）6.25个小朋友排队，从左边数起艾迪是第12个，从右边数起薇儿是第9个，艾迪和薇儿之间有▲个小朋友．【解析】排队问题．25－9－12=4（人）．【答案】47.下面的线条图形中，只有一幅图可以一笔画出，这幅图是▲．（请填入A、B、C或D）A B C D【解析】一笔画问题，数奇点个数，0个或2个奇点可以一笔画．A、B、C、D 分别有4个、4个、4个、2个奇点，D可以一笔画．【答案】D8.4月1日是愚人节，今年的愚人节是星期六．现在有写着数字4、1、6的三张卡片，问：共可以组成▲个不同的三位数．（6可以旋转变成9）【解析】因为数字6的卡片可以倒过来当作数字9．当卡片为4、1、6时，可以组成：416、461、146、164、641、614，6种．当卡片为4、1、9时，可以组成：419、491、149、194、941、914，6种．所以，一共有6+6=12（种）．【答案】129.一只鸡有1个头2条腿，一只兔子有1个头4条腿．如果笼子里的鸡和兔子共有10个头和26条腿，那么鸡有▲只，兔有▲只．【解析】假设法．假设全是鸡，2×10=20（条），26－20=6（条），4－2=2（条），6÷2=3（只）兔，10－3=7（只）鸡．【答案】7；310.艾迪寒假的时候去海边度假，穿着当地特色的衣服，拍了照片．现在我们一起来数一数，照片里一共．．可以数出▲个三角形．【解析】最上面帽子有2个小三角形和1个大三角形，帽子下面有5个小三角形，身体有2个小三角形和1个大三角形，脚有2个小三角形．2＋1＋5＋2＋1＋2=13（个）【答案】13三、思维拓展（每题10分，共50分）11.X别动队队员找到个藏宝屋，发现藏宝屋的门锁是一个密码锁（如下图所示），其中的数是按照一定规律排列的，请按照你找到的规律，将正确的数填入空格内，这个数是 ▲ ．【解析】从1开始按照方向在图中依次填上连续的奇数【答案】1312. 我国的农历用“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”这十二种动物按顺序轮流代表各年的年号．例如，第一年如果是鼠年，那第二年就是牛年，第三年就是虎年，……如果从某年往后数的第1年是鸡年，那么第120年是 ▲ 年．【解析】周期：鸡、狗、猪、鼠、牛、虎、兔、龙、蛇、马、羊、猴；周期是12．120÷12=10（组），没有余数，就是周期中的最后一个，猴． 【答案】猴13. 乘乘用四个相同的长方形和一个小正方形组成一个大正方形，每个长方形的周长为10厘米，大正方形的周长为 ▲ 厘米．【解析】大正方形的边长等于长方形的长+宽，长方形的长+宽是10÷2=5（厘米），大正方形的周长是5×4=20（厘米）． 【答案】2014. 艾迪排在一个十字形队伍的正中间，这个队伍一共有23人，横排人数是竖排人数的2倍，那么横排有 ▲ 人．【解析】排队问题，和倍问题．正中间的艾迪既在横排，又在竖排，所以横排人数+竖排人数为27+1=28（人）；竖排有：28÷（3+1）=7（人），横排有：7×3=21（人）． 【答案】2115. 薇儿一共有22张积分卡，平均分给了一些小朋友，最后还剩4张，那么小朋友的人数有 ▲ 种可能．【解析】22÷（人数）=（每人分的张数）……4，除数比余数大，人数可能是6人、9人、18人，有3种可能． 【答案】3四、 挑战（每题12分，共60分）16. 有一个如图所示形状的花坛，艾迪要绕着这个花坛摆花盆，每隔2米摆一盆，一共要摆 ▲ 盆花．（图中单位均为米）【解析】通过平移，花坛周长是长为20米，宽为10＋6=16（米）的长方形周长，周长为（20＋16）×2=72（米），隔2米摆一盆，共摆72÷2=36（盆）． 【答案】3664101066420101017. 将1、2、3、4、5、6这6个数字分别填入下面的“” 中，使得下面的一句话成立.其中有一个中的数字已经填好.这句话是这样的：玲玲非常喜欢做《计算天天练》，每做完一页需要18分钟，玲玲从开始做，做完一页后正好是．【解析】每个数字填一次，从2点多开始做，做完3点多．做一页需要18分钟，要满足条件，2：56到3：14． 【答案】2；5；6；1；418. 空格中填入数字1-4，使得每行、每列和每个粗线框内数字都不重复．格里的小数表示这个格上下左右四个格中有多少个比它大的数字．图中B 代表的数是 ▲ ．【答案】219. 有4张卡片，每张卡片上各写着一个互不相同的数字．博士首先将这4张卡片发给大毛、二毛、三毛和四毛四个小朋友，然后收回来再分别发给四人各一张，如此一共发了3次．如果把3次收到的卡片上的数字相加，大毛的和是0，二毛的和是3，三毛的和是11，四毛的和是16．请问这四张卡片上最大的数字是 ▲ ．【解析】大毛3次的和是0，大毛每次拿到的都是0；二毛3次的和是1，二毛每次拿到的都是1；三毛、四毛3次的和都不能被3整除，说明三毛、四毛另外两张卡片都拿到过，都是另外两张卡片各拿一次，剩余一次三毛拿了其中小的一张，四毛拿了其中大的一张．三毛的和比四毛的和小5，说明另外两张相差5．满足三毛和是11，四毛和是16，另两张为2，7．【答案】720.下图给出了用火柴棍摆数字0～9 的方法．（1）现有9根火柴棍，要求全用完，则能摆出最小．．的两位数是▲．（2）现有20根火柴棍，要求全用完，则能摆出最小．．的数是▲．【解析】（1）摆0~9分别要用6、2、5、5、4、5、6、3、7、6根火柴棍．要使两位数最小，十位最小为1，用去2根火柴棍，剩下7根只能摆出8，最小为18．（2）要使数最小，数位越少，数越小．用火柴棍摆出两位数最多用2×7=14（根），摆出三位数最多用3×7=21（根）．20根火柴棍摆出最小的数为三位数，并且一定要用14根组成2个8，剩余6根要使数最小，摆成6，最小为688．【答案】18；688。

学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．(2016·厦门高二检测)用火柴棒摆“金鱼”，如图2-1-7所示：图2-1-7按照上面的规律，第n个“金鱼”图需要火柴棒的根数为()A．6n－2B．8n－2C．6n＋2 D．8n＋2【解析】观察易知第1个“金鱼”图中需要火柴棒8根，而第2个“金鱼”图中比第1个“金鱼”图中多的部分需要火柴棒6根，第3个“金鱼”图中比第2个“金鱼”图中多的部分需要火柴棒6根，…….由此可猜测第n个“金鱼”图需要火柴棒的根数比第n－1个“金鱼”图需要火柴棒的根数多6，即各个“金鱼”图需要火柴棒的根数组成以8为首项，6为公差的等差数列，易求得通项公式为a n＝6n＋2.【答案】 C2．数列－3,7，－11,15，…的通项公式可能是()A．a n＝4n－7B．a＝(－1)n(4n＋1)C．a n＝(－1)n(4n－1)D．a n＝(－1)n＋1(4n－1)【解析】当数列中负项、正项交替出现时，用(－1)n来控制；若是正项、负项交替出现，则用(－1)n＋1来控制．【答案】 C3．定义A*B，B*C，C*D，D*B依次对应下列4个图形：图2-1-8那么下列4个图形中，图2-1-9可以表示A*D，A*C的分别是()A．(1)，(2) B．(1)，(3)C．(2)，(4) D．(1)，(4)【解析】由①②③④可归纳得出：符号“*”表示图形的叠加，字母A代表竖线，字母B代表大矩形，字母C代表横线，字母D代表小矩形，∴A*D是(2)，A*C 是(4)．【答案】 C4．下列推理正确的是()A．把a(b＋c)与log a(x＋y)类比，则log a(x＋y)＝log a x＋log a yB．把a(b＋c)与sin(x＋y)类比，则sin(x＋y)＝sin x＋sin yC．把(ab)n与(x＋y)n类比，则(x＋y)n＝x n＋y nD．把(a＋b)＋c与(xy)z类比，则(xy)z＝x(yz)【解析】A错误，因为log a x＋log a y＝log a xy(x>0，y>0)；B错误，因为sin(x＋y)＝sin x cos y＋cos x sin y；C错误，如当n＝2时，若xy≠0，则(x＋y)2＝x2＋2xy＋y2≠x2＋y2；D正确，类比的是加法、乘法的结合律．【答案】 D5．给出下列等式：1×9＋2＝11，12×9＋3＝111， 123×9＋4＝1 111， 1 234×9＋5＝11 111， 12 345×9＋6＝111 111， …猜测123 456×9＋7等于( ) A ．1 111 110 B ．1 111 111 C ．1 111 112D ．1 111 113【解析】 由题中给出的等式猜测，应是各位数都是1的七位数，即1 111 111. 【答案】 B 二、填空题 6．已知2＋23＝2·23，3＋38＝3·38，4＋415＝4·415，….若8＋a t ＝8·at (a ，t 均为正实数)，类比以上等式，可推测a ，t 的值，则a ＋t ＝________.【解析】 由所给等式知，a ＝8，t ＝82－1＝63，∴a ＋t ＝71. 【答案】 717．设n 为正整数，f (n )＝1＋12＋13＋…＋1n ，计算得f (2)＝32，f (4)>2，f (8)>52，f (16)>3，观察上述结果，可推测一般的结论为__________. 【导学号：05410041】【解析】 ∵f (2)＝32，f (4)>2＝42，f (8)>52，f (16)>3＝62，∴由此可推测一般性的结论为f (2n)≥n ＋22.【答案】 f (2n )≥n ＋228．对于命题“如果O 是线段AB 上一点，则| OB →|·OA →＋|OA →|·OB →＝0”，将它类比到平面的情形是：若O 是△ABC 内一点，有S △OBC ·OA →＋S △OCA ·OB →＋S △OBA ·OC →＝0，将它类比到空间的情形应为：若O 是四面体ABCD 内一点，则有________________________________________________．【解析】 根据类比的特点和规律，所得结论形式上一致，又线段类比平面，平面类比到空间，又线段长类比为三角形面积，再类比成四面体的体积，故可以类比为V O -BCD ·OA →＋V O -ACD ·OB →＋V O -ABD ·OC →＋V O -ABC ·OD →＝0.【答案】 V O -BCD ·OA →＋V O -ACD ·OB →＋V O -ABD ·OC →＋V O -ABC ·OD →＝0 三、解答题9．平面中的三角形和空间中的四面体有很多相类似的性质，例如在三角形中： (1)三角形两边之和大于第三边． (2)三角形的面积S ＝12×底×高．(3)三角形的中位线平行于第三边且等于第三边的12. …请类比上述性质，写出空间中四面体的相关结论．【解】 由三角形的性质，可类比得空间四面体的相关性质为： (1)四面体的任意三个面的面积之和大于第四个面的面积． (2)四面体的体积V ＝13×底面积×高．(3)四面体的中位面平行于第四个面且面积等于第四个面的面积的14.10．某少数民族的刺绣有着悠久的历史，如图2-1-10(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣(小正方形的摆放规律相同)，设第n 个图形包含f (n )个小正方形．图2-1-10(1)求出f (5)；(2)利用合情推理的“归纳推理思想”归纳出f(n＋1)与f(n)的关系式，并根据你得到的关系式求f(n)的表达式．【解】(1)∵f(1)＝1，f(2)＝5，f(3)＝13，f(4)＝25，∴f(5)＝25＋4×4＝41.(2)∵f(2)－f(1)＝4＝4×1，f(3)－f(2)＝8＝4×2，f(4)－f(3)＝12＝4×3，f(5)－f(4)＝16＝4×4，由上式规律得出f(n＋1)－f(n)＝4n.∴f(2)－f(1)＝4×1，f(3)－f(2)＝4×2，f(4)－f(3)＝4×3，…f(n－1)－f(n－2)＝4·(n－2)，f(n)－f(n－1)＝4·(n－1)．∴f(n)－f(1)＝4[1＋2＋…＋(n－2)＋(n－1)]＝2(n－1)·n，∴f(n)＝2n2－2n＋1.[能力提升]1．观察下列各式：1＝12，2＋3＋4＝32，3＋4＋5＋6＋7＝52，4＋5＋6＋7＋8＋9＋10＝72，…可以得出的一般结论是()A．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝n2B．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2C．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝n2D．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝(2n－1)2【解析】观察已知等式，第n个等式左边都是2n－1个数相加，第1个数是n，等式右边是(2n－1)2.由此可得一般结论为：n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2，故选B.【答案】 B2．已知x>0，由不等式x＋1x≥2x·1x＝2，x＋4x2＝x2＋x2＋4x2≥33x2·x2·4x2＝3，…，我们可以得出推广结论：x＋ax n≥n＋1(n∈N＋)，则a＝()A．2n B．n2 C．3n D．n n【解析】∵x＋1x≥2x·1x＝2，x＋4x2＝x2＋x2＋4x2≥33x2·x2·4x2＝3.…由此猜想，x＋ax n＝所以a＝n n，选D.【答案】 D3．在Rt△ABC中，∠C＝90°，AC＝b，BC＝a，则△ABC的外接圆半径为r＝a2＋b22，将此结论类比到空间，得到相类似的结论为：________.【导学号：05410042】【解析】利用类比推理，可把Rt△ABC类比为三棱锥P-ABC，且P A，PB，PC两两垂直，当P A＝a，PB＝b，PC＝c时，其外接球半径为R＝a2＋b2＋c22.【答案】在三棱锥P-ABC中，P A，PB，PC两两垂直，P A＝a，PB＝b，PC＝c，则三棱锥P-ABC的外接球的半径为R＝a2＋b2＋c224．如图2-1-11所示，为m行m＋1列的士兵方阵(m∈N＋，m≥2)．图2-1-11(1)写出一个数列，用它表示当m分别是2,3,4,5，…时，方阵中士兵的人数；(2)若把(1)中的数列记为{a n}，归纳该数列的通项公式；(3)求a10，并说明a10表示的实际意义；(4)已知a n＝9 900，问a n是数列的第几项？【解】(1)当m＝2时，表示一个2行3列的士兵方阵，共有6人，依次可以得到当m＝3,4,5，…时的士兵人数分别为12,20,30，….故所求数列为6,12,20,30，….(2)因为a1＝2×3，a2＝3×4，a3＝4×5，…，所以猜想a n＝(n＋1)·(n＋2)，n.∈N＋(3)a10＝11×12＝132.a10表示11行12列的士兵方阵的人数为132.(4)令(n＋1)(n＋2)＝9 900，解得n＝98，即a n是数列的第98项.。