郑君里信号与系统习题答案
- 格式:doc
- 大小:1.47 MB
- 文档页数:11

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?第L f (t)N0 ■(a) t只取1, 2, 3, 4值4321(b)iL f (t) 只取1, 2, 3值3, ! H I2I h I i10 1 2 3 4 5 6 7 8 t(C)1 I只取0,P11值___________________ k.0 12345678 n"1L f (t)h■-0 1 2 3 4 5 6 7 8 t(d)X (n)只取-1, 1值14 5 6 8 ■0 1 2 3 7 n r -1 4 JI-(f)申X(n)图1-2解信号分类如下:(a ) 连续信号(模拟信号); (b ) 连续(量化)信号; (C )离散信号,数字信号; (d ) 离散信号;(e ) 离散信号,数字信号; (f ) 离散信号,数字信号。
1-2分别判断下列各函数式属于何种信号?(重复 1-1题所示问) (1) e at Sin ( t ); (2) e nτ ; (3) cos (n );(4) Sin (n 。
)(。
为任意值); (5) I 2。
2解由1-1题的分析可知: (1) 连续信号; (2) 离散信号;(3) 离散信号,数字信号; (4) 离散信号; (5) 离散信号。
1-3分别求下列各周期信号的周期T : (1) COs (Iot ) cos (30t ); (2) e j10t ; (3) [5sin (8t )]2 ;(4) ( 1)n u (t nT ) u (t nT T )( n 为整数)。
n 0解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察 各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数; 若不存在,信号离散模拟:幅值、时间均连 量化:幅值离散,时间 续(例见图1 2( a ))抽样 数字 时间离散,幅值 幅值、时间均离 连续(例见图1 连续(例见图1囂)图1-1所示信号分别为 散(例见图1 2( d ))则该复合信号为非周期信号。

郑君⾥信号与系统习题答案第三章傅⾥叶变换⼀.周期信号的傅⾥叶级数⼆.傅⾥叶变换例题例题1:傅⾥叶级数——频谱图 ?例题2:傅⾥叶变换的性质 ?例题3:傅⾥叶变换的定义 ?例题4:傅⾥叶变换的性质 ?例题5:傅⾥叶变换的性质 ?例题6:傅⾥叶变换的性质例题7:傅⾥叶变换的性质、频响特性 ?例题8:傅⾥叶变换的性质 ?例题9:抽样定理–例题10:周期信号的傅⾥叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱;()?--??? ??++=328cos 265sin cos 3ππt t t t f 形式频谱:离散性、谐波性、收敛性周期矩形脉冲信号的频谱特点定义及傅⾥叶变换存在的条件典型⾮周期信号的频谱冲激函数和阶跃信号的傅⾥叶变换性质→应⽤:调制和解调→频分复⽤周期信号的傅⾥叶变换:由⼀些冲激函数组成抽样信号的傅⾥叶变换→抽样定理→应⽤:时分复⽤2. 画出双边幅度谱和相位谱。
双边幅度谱和相位谱例3-2 分析:f (t )不满⾜绝对可积条件,故⽆法⽤定义求其傅⾥叶变换,只能利⽤已知典型信号的傅⾥叶变换和性质求解。
下⾯⽤三种⽅法求解此题。
⽅法⼀:利⽤傅⾥叶变换的微分性质⽅法⼆:利⽤傅⾥叶变换的积分性质⽅法三:线性性质⽅法⼀:利⽤傅⾥叶变换的微分性质要注意直流,设f A(t )为交流分量,f D(t )为直流分量,则其中()?+-+? -++=ππππ328cos 2265cos cos 3t t t t f ?++??? ??-+=38cos 2315cos cos 3ππt t t()。
的傅⾥叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()??? ??-='211t G t f A ()ωωωωj Ae F j -??=∴2Sa⽅法⼆:利⽤傅⾥叶变换的积分性质⽅法三:利⽤线性性质进⾏分解此信号也可以利⽤线性性质进⾏分解,例如例3-3已知信号f (t )波形如下,其频谱密度为F (j ω),不必求出F (j ω)的表达式,试计算下列值:()ωωωωj e F j A -??=∴2Sa ()()()()ωπδωωωωωω32Sa +??? ??=+=∴-j e F F F j D为)()(21t f t f ()ωωωj e F -??? ??=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --??? ??+=??? ???+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -??? ??+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()?∞∞-ωωd 2F -t tj d ω(()?∞-====∴5.1d 00t t f F F ωω令t =0,则则例3-4按反褶-尺度-时移次序求解已知⽅法⼆:按反褶-时移-尺度次序求解已知⽅法三利⽤傅⾥叶变换的性质其它⽅法⾃⼰练习。

第一章1-1 分别判断图1-1所示各波形就是连续时间信号还就是离散时间信号,若就是离散时间信号就是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a)连续信号(模拟信号); (b)连续(量化)信号; (c)离散信号,数字信号; (d)离散信号;(e)离散信号,数字信号; (f)离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1); (2); (3); (4); (5)。
解由1-1题得分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号得周期T : (1); (2); (3); (4)。
解 判断一个包含有多个不同频率分量得复合信号就是否为一个周期信号,需要考察各分量信号得周期就是否存在公倍数,若存在,则该复合信号得周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于为得最小公倍数,所以此信号得周期。
(2)由欧拉公式 即得周期。
(3)因为 所以周期。
(4)由于原函数 n 为正整数其图形如图1-3所示,所以周期为2T 。
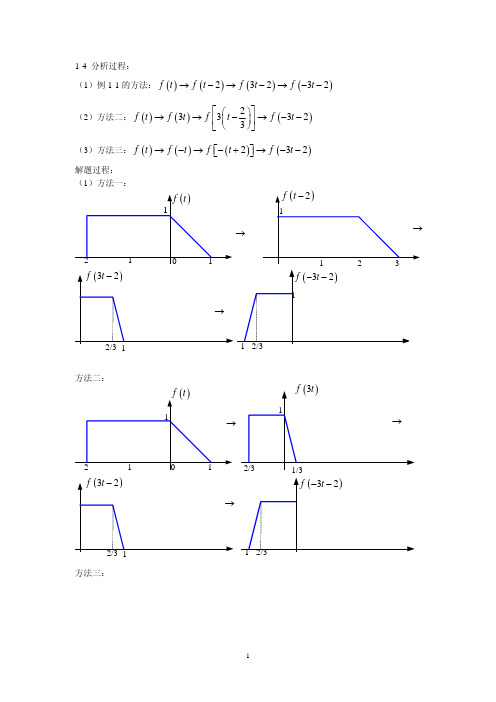
图1-31-4对于教材例1-1所示信号,由f (t )求f (-3t-2),但改变运算顺序,先求f (3t )或先求f (-t ), 讨论所得结果就是否与原例之结果一致。
解 原信号参见例1-1,下面分别用两种不同于例中所示得运算顺序,由f (t )得波形求得f (-3t-2)得波形。
两种方法分别示于图1-4与图1-5中。
方法一:倍乘32左移方法二:反褶32左移图1-4图1-51-5 已知f (t ),为求应按下列那种运算求得正确结果(式中都为正值)? (1)左移; (2)右移;(3)左移;(4)右移。
![信号与系统版课后答案_(郑君里)_高等教育出版社[1]](https://img.taocdn.com/s1/m/40d989225901020207409c1e.png)

【信号与系统(郑君⾥)课后答案】第三章习题解答3-1 解题过程:(1)三⾓形式的傅⽴叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅⽴叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn == F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e ? jn ω1t dt T 1 t 0F n =1( a n ? jb n ) F ? n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因⽽a 0 = a n = 0 4 Tb n = T ∫02= 2Eπ n4TE2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 ? cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三⾓形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5Tn = 0, ±2, ±4,F n = ? jb n jE=2 n = 0,± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = ? jE π ej ω1t+ πjE e ? j ω1t ? 3jE π e j 3ω1t + 3jEπ e ? j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅⽴叶变换有如下两种⽅法。
《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1~3-3,3-5,3-9,3-12,3-13,3-15~3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。
若:求直流分量大小以及基波、二次和三次谐波的有效值。
解:直流分量 ⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数,∴0=nb)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-== )(21T n Sa T E a F n n πςτ==基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1=,E=1V ;)(2t f 的参数为s μτ5.1=,s T μ3=,E=3V ,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3) )(1t f 和 )(2t f 的基波幅度之比; (4) )(1t f 基波与)(2t f 三次谐波幅度之比。
解:(1))(1t f s μτ5.0= s T μ1= E=1V 谱线间隔:khZ T 10001==∆带宽:KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔:khZ T 310001==∆谱线带宽:KHzB f 320001==τ(3) )(1t f 基波幅度:ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度:ππτ6)2cos(4201==⎰dt t T E T a幅度比:1:3(4) )(2t f 三次谐波幅度:ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比:1:13-5 求题图3-5所示半波余弦信号的傅立叶级数。
第三章 傅里叶变换一.周期信号的傅里叶级数二.傅里叶变换例题•例题1:傅里叶级数——频谱图 •例题2:傅里叶变换的性质 •例题3:傅里叶变换的定义 •例题4:傅里叶变换的性质 •例题5:傅里叶变换的性质 •例题6:傅里叶变换的性质•例题7:傅里叶变换的性质、频响特性 •例题8:傅里叶变换的性质 •例题9:抽样定理–例题10:周期信号的傅里叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱;()⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛++=328cos 265sin cos 3ππt t t t f 形式频谱:离散性、谐波性、收敛性 周期矩形脉冲信号的频谱特点定义及傅里叶变换存在的条件 典型非周期信号的频谱冲激函数和阶跃信号的傅里叶变换 性质→应用:调制和解调→频分复用 周期信号的傅里叶变换:由一些冲激函数组成 抽样信号的傅里叶变换→抽样定理→应用:时分复用2. 画出双边幅度谱和相位谱。
单边幅度谱和相位谱双边幅度谱和相位谱例3-2 分析:f (t )不满足绝对可积条件,故无法用定义求 其傅里叶变换,只能利用已知典型信号的傅里叶 变换和性质求解。
下面用三种方法求解此题。
方法一:利用傅里叶变换的微分性质 方法二:利用傅里叶变换的积分性质 方法三:线性性质方法一:利用傅里叶变换的微分性质要注意直流,设f A(t )为交流分量,f D(t )为直流分量,则 其中()⎪⎭⎫⎝⎛+-+⎪⎭⎫ ⎝⎛-++=ππππ328cos 2265cos cos 3t t t t f ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-+=38cos 2315cos cos 3ππt t t()。
的傅里叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()⎪⎭⎫ ⎝⎛-='211t G t f A ()ωωωωj Ae F j -⎪⎭⎫ ⎝⎛=∴2Sa方法二:利用傅里叶变换的积分性质方法三:利用线性性质进行分解此信号也可以利用线性性质进行分解,例如例3-3已知信号f (t )波形如下,其频谱密度为F (j ω),不必求出F (j ω)的表达式,试计算下列值:()ωωωωj e F j A -⎪⎭⎫⎝⎛=∴2Sa ()()()()ωπδωωωωωω32Sa +⎪⎭⎫ ⎝⎛=+=∴-j e F F F j DA ())(11t f t f +=的积分为)()(21t f t f ()ωωωj e F -⎪⎭⎫ ⎝⎛=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -⎪⎭⎫ ⎝⎛+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()⎰∞∞-ωωd 2F -t tj d ω(()⎰∞-====∴5.1d 00t t f F F ωω令t =0,则 则例3-4按反褶-尺度-时移次序求解已知方法二:按反褶-时移-尺度次序求解已知方法三利用傅里叶变换的性质其它方法自己练习。
《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5) ⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2- (6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果(3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5) ⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2- (6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果(3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果 1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
第三章 傅里叶变换一.周期信号的傅里叶级数二.傅里叶变换例题•例题1:傅里叶级数——频谱图 •例题2:傅里叶变换的性质 •例题3:傅里叶变换的定义 •例题4:傅里叶变换的性质 •例题5:傅里叶变换的性质 •例题6:傅里叶变换的性质•例题7:傅里叶变换的性质、频响特性 •例题8:傅里叶变换的性质 •例题9:抽样定理–例题10:周期信号的傅里叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱;()⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛++=328cos 265sin cos 3ππt t t t f 形式频谱:离散性、谐波性、收敛性 周期矩形脉冲信号的频谱特点定义及傅里叶变换存在的条件 典型非周期信号的频谱冲激函数和阶跃信号的傅里叶变换 性质→应用:调制和解调→频分复用 周期信号的傅里叶变换:由一些冲激函数组成 抽样信号的傅里叶变换→抽样定理→应用:时分复用2. 画出双边幅度谱和相位谱。
单边幅度谱和相位谱双边幅度谱和相位谱例3-2 分析:f (t )不满足绝对可积条件,故无法用定义求 其傅里叶变换,只能利用已知典型信号的傅里叶 变换和性质求解。
下面用三种方法求解此题。
方法一:利用傅里叶变换的微分性质 方法二:利用傅里叶变换的积分性质 方法三:线性性质方法一:利用傅里叶变换的微分性质要注意直流,设f A(t )为交流分量,f D(t )为直流分量,则 其中()⎪⎭⎫⎝⎛+-+⎪⎭⎫ ⎝⎛-++=ππππ328cos 2265cos cos 3t t t t f ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-+=38cos 2315cos cos 3ππt t t()。
的傅里叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()⎪⎭⎫ ⎝⎛-='211t G t f A ()ωωωωj Ae F j -⎪⎭⎫ ⎝⎛=∴2Sa方法二:利用傅里叶变换的积分性质方法三:利用线性性质进行分解此信号也可以利用线性性质进行分解,例如例3-3已知信号f (t )波形如下,其频谱密度为F (j ω),不必求出F (j ω)的表达式,试计算下列值:()ωωωωj e F j A -⎪⎭⎫⎝⎛=∴2Sa ()()()()ωπδωωωωωω32Sa +⎪⎭⎫ ⎝⎛=+=∴-j e F F F j DA ())(11t f t f +=的积分为)()(21t f t f ()ωωωj e F -⎪⎭⎫ ⎝⎛=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -⎪⎭⎫ ⎝⎛+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()⎰∞∞-ωωd 2F -t tj d ω(()⎰∞-====∴5.1d 00t t f F F ωω令t =0,则 则例3-4按反褶-尺度-时移次序求解已知方法二:按反褶-时移-尺度次序求解已知方法三利用傅里叶变换的性质其它方法自己练习。
例3-5解:()()()⎰∞∞-=ωωπωd 212etj F t f ()()⎰∞∞-=ωωπd 210F f ()()ππωω202d ==⎰∞∞-f F ()()[]()()[]。
利用傅里叶变换的性质已知t f F t f F F 26,,111-==ωω()[]()ω-=-11F t f F ()[]⎪⎭⎫ ⎝⎛-=-221211ωF t f F ()[]ωω31122126j e F t f F -⎪⎭⎫ ⎝⎛-=-反褶对t 倍压缩对2t 得时移对,26t ()()[]t f F F 11=ω()[]()ω-=-11F t f F ()[]()ωω6116j e F t f F --=-()[]ωω31122126j eF t f F -⎪⎭⎫ ⎝⎛-=-()()[]t f F F 11=ω得时移对,6t 反褶对t 倍压缩对2t ()[]a t j ea F a t at f F 010ωω-⎪⎭⎫ ⎝⎛=-代入上式,得这里6-2,a 0-==t ()[]ωω31122126j eF t f F -⎪⎭⎫ ⎝⎛-=-()()的频谱比较。
冲信号密度函数,并与矩形脉利用频移性质求其频谱已知升余弦信号⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=≤≤⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=22)(,0 cos 121ττττπt u t u E t f t t E t f()()()[]τττπτπ--+⎥⎦⎤⎢⎣⎡++=-t u t u e E e E E t f t t j j 442()ωττSa E ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-ττπωτSa 2E ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+ττπωτSa 2E升余弦脉冲的频谱τE τ2E τ2E比较1F例3-6 已知双Sa 信号()()()[]{}τωωπω2--=t Sa t Sa t f c c c ()t Sa c cωπω=已知由时移特性得到从中可以得到幅度谱为双Sa 信号的波形和频谱如图(d ) (e )所示。
()()()()()()所示。
的波形如图和为矩形。
波形,其频谱为因b t f tf F t f ,a Sa 000ω(a)(b)()所示。
的波形如图(c)20τ-t f ()[]⎩⎨⎧<<= )( 0)( 10c c t f F ωωωω(c)()[]⎪⎩⎪⎨⎧<<=-- )( 0)( 220c c j et f F ωωωωτωτ()的频谱等于因此t f ()()[]()[]⎪⎩⎪⎨⎧<<-=--=-)( 0)( 12200c c j e t f F t f F F ωωωωτωωτ()()⎩⎨⎧<<= )( 0)( sin 2c c F ωωωωωτω此时上式变成在实际中往往取,c ωπτ=()⎪⎩⎪⎨⎧<<⎪⎪⎭⎫⎝⎛=)( 0)( sin 2c c c F ωωωωωπωω(d )(e)例3-7-8由对称关系求又因为频谱图 由对称关系求幅频、相频特性幅频、相频特性分别如图(c)(d)所示。
(c) (d)幅度频谱无变化,只影响相位频谱例3-8已知信号 求该信号的傅里叶变换。
()).( , 1b t f 如图引入辅助信号()ω1F )()( 21ωωπG F =)1()(1-=t f t f ωπωωωωj j e G e F F --⋅=⋅=)()()(21()ω1F |)(|ωF ω)(ωφ⎩⎨⎧-000t t t ωωω左右相移⎪⎩⎪⎨⎧>≤+=ππt t t t f 0cos 1)(分析:该信号是一个截断函数,我们既可以把该信号看成是周期信号 经过门函数 的截取,也可以看成是 被信号 调制所得的信号.有以下三种解法: 方法一:利用频移性质 方法二:利用频域卷积定理方法三:利用傅里叶变换的时域微积分特性 方法一:利用频移性质利用频移性质:由于 利用欧拉公式,将 化为虚指数信号, 就可以看成是门函数 被虚指数信号调制的结果。
在频域上,就相当于对 的频谱进行平移。
又因所以根据频移性质,可得方法二:用频域卷积定理 将 看成是信号 经过窗函数 的截取,即时域中两信号相乘根据频域卷积定理有方法三:利用傅里叶变换的时域微积分特性 信号f (t )是余弦函数的截断函数,而余弦函数的二次导数又是余弦函数。
利用傅里叶变换的时域微积分特性可以列方程求解。
()t cos 1+()t G π2()t G π2()t cos 1+())(cos 1)(2t G t t f π+=()t cos 1+)(t f ()t G π2()t G π2())(21211)(cos 1)(22t G e e t G t t f jt jt ππ⎪⎭⎫ ⎝⎛++=+=-()ωπωπωππsin 2Sa 2)(2=↔t G ()[]()()()1sin 211sin 22111sin 221sin 2)(2--=++⋅+--⋅+==ωωπωωωπωωπωπωωt f F F )(t f ()t cos 1+()t G π2())(cos 1)(2t G t t f π+=()[]()[]t G F t F F ππω2cos 121*+=()()()[]11221++-+=ωπδωπδωπδπωπωsin 2*()1sin 22--=ωωπω()()()的波形为:t f t f t f ''',,对上式两端取傅里叶变换,可得即例3-9(1)要求出信号的频宽,首先应求出信号的傅里叶变换F (ω) 已知即利用傅里叶变换的对称性f (t )的波形和频谱图如下所以信号的频带宽度为()[])(22t G t f ππ--=()()()⎥⎦⎤⎢⎣⎡--=ωπωωωωsin 22F F j ()()ωπωωωsin 212=-F ()())项移到方程右边,即项,因此可将(中不可能含有根据时域积分特性,处都等于叶变换在均为能量信号,其傅里和由于21,00)()(ωωδωω-='''F t f t f ()()1sin 22--=ωωπωωF 。
和奈奎斯特奈奎斯特频率进行均匀冲激抽样,求分),若对的频宽(只计正频率部求信号N f t f t t f )()100(Sa )(=()⎪⎭⎫⎝⎛↔2Sa ωτττt G ωωτ1002=令200,=则τ()()ω100Sa 200200↔∴t G ()()ω100Sa 2001200↔t G ()()()ωπωπ20020010020012100Sa G G t =⋅↔Hz 502ππω==∴m m f s rad/100=m ω(2)最高抽样频率(奈奎斯特频率)为奈奎斯特间隔(即最大允许抽样间隔)为 例3-10已知周期信号f (t )的波形如下图所示,求f (t )的傅里叶变换F (ω)。
分析:求信号的傅里叶变换一般有两种解法。
方法一:将信号转化为单周期信号与单位冲激串 的卷积,用时域卷积定理来求解; 方法二:利用周期信号的傅里叶级数求解。
方法一将信号转化为单周期信号与单位冲激串的卷积。