全站仪三角高程记录计算表
- 格式:doc
- 大小:64.00 KB
- 文档页数:2

三角高程测距法计算公式在地理测量和导航领域,测距是一项非常重要的工作。
而三角高程测距法是一种常用的测距方法之一。
本文将介绍三角高程测距法的计算公式及其应用。
三角高程测距法是利用三角形的相似性原理,通过测量两个点之间的水平距离和垂直高程差来计算两点之间的实际距离。
这种方法通常用于测量山区或者其他地形复杂的地区,因为在这些地方使用其他测距方法可能会受到一些限制。
三角高程测距法的计算公式如下:d = √(ΔH^2 + ΔL^2)。
其中,d表示两点之间的实际距离,ΔH表示两点之间的垂直高程差,ΔL表示两点之间的水平距离。
在实际应用中,首先需要测量两个点之间的水平距离,通常可以使用测距仪或者全站仪来进行测量。
然后需要测量两个点之间的垂直高程差,这可以通过水准仪或者其他高程测量工具来实现。
最后,将这两个数据代入上述的计算公式中,就可以得到两点之间的实际距离。
三角高程测距法的应用非常广泛。
比如在地图制作中,为了准确绘制地图上的山脉、河流等地理要素,需要使用三角高程测距法来获取这些地理要素之间的实际距离。
另外,在军事领域和野外探险中,也常常需要使用三角高程测距法来获取地形的实际距离,以便进行作战或者导航。
除了上述的基本公式之外,三角高程测距法还有一些变种和衍生公式。
比如在实际测量中,可能会遇到一些地形复杂的地区,这时候就需要考虑地形因素对测距结果的影响。
在这种情况下,可以使用斜距修正公式来修正实际距离,以提高测距的准确性。
总之,三角高程测距法是一种简单而有效的测距方法,它通过测量水平距离和垂直高程差来计算实际距离,广泛应用于地理测量、地图制作、军事作战和野外探险等领域。
通过掌握三角高程测距法的计算公式及其应用,可以更好地进行地理测量和导航工作,提高测距的准确性和可靠性。

Excel电子表格在测量内业计算中的应用陕西蒲白西固煤业有限责任公司张龙刚武卫欣摘要采用Excel电子表格插入函数,对测量原始数据加工处理,可计算出坐标、三角高程、腰线高程以及坐标反算方位和平距等,可大大简化测量内业计算工作,只要电脑安装有Excel办公软件均可实现该项工作,简单、实用、方便。
关键词Excel电子表格导线计算三角高程坐标反算1前言随着科学技术水平的高速发展,测绘技术水平在快速进步,各类测绘手段也在不断的发展和更新,从经纬仪、全站仪、GPS、航空测量再到现在的无人机测绘,测绘技术已愈发普遍和成熟。
测量工作外业数据采集的方法和精度越来越简单和准确,作为测量数据处理的内业来说,提高工作效率和正确率,就显得更为重要。
很多测量工作者也在编程和使用一些小的程序和软件或者表格等计算工具完成简单的数据处理。
笔者在陕西蒲白西固煤业公司从事矿山测量工作。
井下测量多为复测支导线,现将平时自己编制使用的一些Excel电子表格在测量内业计算中的实例和经验做一简单总结,以供分享。
2导线测量计算表导线测量首先需要已知起始点,坐标和起始方位,在验证完起始数据和点位准确无误后,进行导线测设,获得导线夹角、斜距或平距、前视高、仪器高、垂直角或垂距等数据,然后进行内业计算。
以前在内业处理时,测量人员将所测的所有数据经计算器计算、对算后,手工填写纸质导线台账,计算工序繁琐且容易出错。
如果采用Excel电子表格相关功能进行导线计算,可大大提高工作效率,降低出错率。
现就导线计算的Excel电子表格具体形式、表格编辑举例说明如下:2.1前期数据采集准备工作为配合该表格和减少中间计算环节,全站仪导线测量时,测距采用平距模式,高差采集为垂距,直接在全站仪上采集生成水平距离和垂距。
2.2表格编辑和相关函数表-1导线测量计算表将起始方位(F4G4H4)(见表-1,后同)和起始坐标(N4、O4)录入表中作为整张表计算的最基础数据,然后分别将导1点测站测得的导线夹角(C5D5E5)录入表中,用计算器算出导线方位角(F5G5H5);之后录入水平距离(I5)、仪器高(J5)、前视高(K5)、垂距(L5),然后表格自动算出高差(M5)、X坐标(N5)和Y坐标(O5):高差计算:Δh=垂距+前视高-仪器高,故M5=L5+K5-J5;平面坐标X计算:X=cosα+X前,故N5=I5*cos (RADIANS(F5+G5/60+H5/3600))+N4;平面坐标Y计算:X=sinα+Y前,故O5=I5*sin (RADIANS(F5+G5/60+H5/3600))+O4;高程H计算:H=△h+H前,故P5=M5+P4。

三角高程全站仪方法
三角高程全站仪方法是一种常用的测量方法,适用于较为平坦的地形,能够精确地测量地面高程。
以下是具体步骤:
1. 在测量范围内设置三个固定测站,并利用全站仪进行点名、定向和坐标测量,得到这三个测站的坐标和高程数据。
2. 然后在需要测量高程的目标点上,再次使用全站仪进行点名和定向测量,得到该点的坐标和水平角度。
3. 然后,利用全站仪测量目标点到三个固定测站的斜距,计算出目标点到三个测站的夹角,即目标点所处的三角形内角。
4. 利用三角形内角定理和正弦定理,计算出目标点的高程。
需要注意的是,在使用全站仪测量时,需要保持仪器的水平,并进行准确的点名和定向。
另外,由于测量误差的存在,建议多次测量并取平均值,以提高测量精度。



三角高程测量是一种常用的测量方法,它可以用来测量地面上点的准确高程。
在这篇文章中,我们将着重介绍三角高程测量中的往返观测计算公式。
一、三角高程测量原理三角高程测量是利用三角形的相似性原理,通过已知两点的高程和这两点到待测点的水平距离,来计算待测点的高程。
三角高程测量的基本原理如下:1. 在地面上选择一个已知高程的点A,以及要测量高程的点P。
2. 通过测量仪器测量点A和点P之间的水平距离d和两点的高程差h。
3. 通过三角函数计算出点P的高程。
二、三角高程测量的往返观测在实际测量中,为了提高精度,常常采用往返观测的方法进行测量。
往返观测的原理是利用观测仪器来回测量两点之间的距离和高程差,然后取平均值作为最终结果,以减小由于观测仪器误差、大气温度、大气压力等因素造成的误差。
三、三角高程测量往返观测计算公式往返观测的三角高程测量计算公式如下:1. 求点P的高程差首先需要计算出点P的高程差,使用以下公式:\[ \Delta h = h_1 - h_2 \]其中,\(h_1\) 为第一次测量的高程,\(h_2\) 为第二次测量的高程。
2. 求两次测量的平均距离将两次测量的距离\(d_1\)和\(d_2\)求均值,得到平均距离:\[ \bar{d} = \frac{d_1 + d_2}{2} \]3. 计算点P的高程利用三角函数计算出点P的高程:\[ H = h_2 + \frac{\Delta h \times \bar{d}}{d_2} \]其中,\(H\)为最终计算出的点P的高程。
四、注意事项在进行三角高程测量的往返观测时,需要注意以下几点:1. 观测仪器的选择和校准非常重要,需要保证其精度和稳定性。
2. 大气温度和大气压力对测量结果有较大影响,需要进行相应的修正。
3. 观测时需要注意周围环境的影响,避免受到建筑物、树木、地形等因素干扰。
4. 测量终点的选取应当避免大坡度地形,以减小误差。
通过以上介绍,我们了解了三角高程测量中的往返观测计算公式及其应用注意事项。

三角高程全站仪方法
三角高程测量是一种通过三角形相似,利用已知的变量来求解未
知量的方法。
全站仪可以测量距离、角度和高程等参数,因此被广泛
用于三角高程测量中。
具体方法如下:
1. 确定测量点:在需要进行三角高程测量的地区,选择两个已
知高程点和一个需要求解高程的未知点。
2. 进行见证点观测:在已知高程点与未知点之间设置几个见证点,并在这些点上安装全站仪。
在使用全站仪测量时,需要保证全站
仪朝向测站的望远镜指向要测点的方向,并进行水平校正。
3. 进行三角形观测:全站仪进行观测时,需要记录望远镜与三
个预先设置的见证点之间的角度,以及每个见证点与需要测量的未知
点之间的距离。
4. 计算高程:在完成三角形观测后,根据三角形相似原理,可
以得出未知点的高程值。
计算过程需要用到三角函数和高程测量公式,具体方法比较复杂,可以参考相关的高等数学和测量学课程来学习。
在三角高程测量过程中需要注意的是,全站仪的误差对测量结果
影响非常大,因此需要严格按照使用手册进行操作,并进行精度调整。
此外,在选择已知高程点和定位见证点时,应尽可能选择地势平坦、
视线通畅的地方,以避免误差和干扰。


全站仪三角高程测量方法全站仪三角高程测量是一种常见的测量方法,它是利用全站仪的功能完成的。
全站仪是一种先进的测量仪器,可以同时测量水平角、垂直角和斜距,具有高精度和高效率的特点。
三角高程测量是通过测量三角形的角度和边长来计算出待测点的高程。
全站仪三角高程测量的步骤如下:1. 建立三角测量网:首先,需要在待测区域内建立起一定数量的控制点,这些控制点要能够互相看见,形成一个闭合的三角形控制网。
控制点的位置可以根据地形和实际需求来选择,一般要选取在地势较高且不易遮挡的地方。
2. 选择目标点:选择待测点,即需要测量高程的点。
目标点的选择要考虑到测量的准确性和可行性,一般要选择在可观测的控制点旁边,以保证测量的精度。
3. 进行观测:使用全站仪观测待测点与控制点之间的角度和斜距。
观测时,首先要对控制点进行测量,测量控制点的位置和高程,以确定其空间坐标。
然后,将全站仪转至待测点,观测待测点与控制点之间的角度和斜距。
观测时,要注意保持仪器的水平和垂直,控制观测的时间和操作使其尽量减小。
4. 数据处理:观测完成后,需要对观测数据进行处理。
处理的主要内容包括角度观测值的平差、斜距观测值的平差和高程计算。
角度观测值的平差可以使用三角闭合平差法或最小二乘法进行,斜距观测值的平差可以使用杆长观测法或三边观测法进行平差。
在计算高程时,需要使用三角形的高程计算公式,结合已知的控制点高程和测得的控制点与待测点之间的高差,来计算待测点的高程值。
5. 矫正高程:为了提高测量的精度,需要对观测到的高程进行矫正。
主要的矫正方式有大地水准面、大地水准面高差改正、六参数高差改正等。
根据实际情况,选择合适的矫正方法进行矫正。
全站仪三角高程测量方法具有测量精度高、操作简便、测量效率高的特点,因此被广泛应用于各种测量工程中。
但是,在实际测量中,还需要注意一些技术要点,如全站仪的校准、观测时的操作规范、数据处理的准确性等,以确保测量结果的准确性和可靠性。
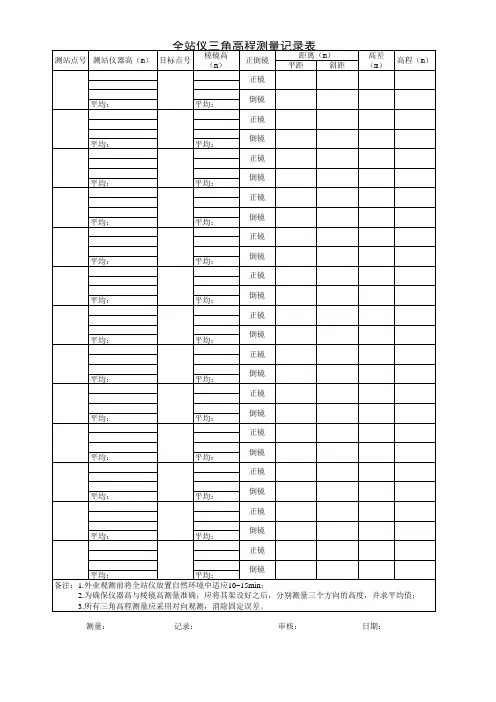
全站仪三角搞成测量记录数据测站照准点号镜高(m) 高差读数(m)平均值(m)高差(m)高程(m)L R自由设站轴2 1.6350.08730.0910.0890.288自由设站轴4 1.570.0260.0260.026-0.630.0290自由设站靶140.00000.15560.1560.1560.067 1.9900.0667自由设站靶120.00000.1660.1660.1660.077 2.000自由设站靶100.00000.2960.2970.2970.207 2.130自由设站靶050.00000.1330.1330.1330.044 1.967自由设站靶040.00000.1070.1080.1080.019 1.942自由设站靶090.00000.120.120.1200.031 1.954自由设站靶110.00000.1530.1530.1530.064 1.987自由设站靶130.00000.2540.2540.2540.65 2.088自由设站白球0.0000-0.514-0.514-0.514-0.0603 1.320后视高差减去前视高差等于前视为要测量的目标测量坐标方法;架设在已知点上,建立作业文件夹名,然后输入已知点坐再根据提示输入定向点坐标(后视点坐标),然后照准后视点瞄准测量提示设站成《此方法是已知点坐标定向模式》照准那个点,屏幕出现的就是那个点的坐测量要求;要有三个通视的符合精度的已知点,水准和导线都要符合这个要求,因0.355 1.99用后视棱镜高加上前视点地上高程等于目标点与地面高程等于前视地面高程是拿后视高程加上后视和测量点之间差减去前视高差等于前视高差,后视为定向点目标,的目标,公式后视-前视等于测量点和后视的高差,入已知点坐标,然后点击测量程序设站,输入(或调出已经录入有的坐标名),瞄准测量提示设站成功,然后再对准要测量的点,就能出现任一点坐标值,是那个点的坐标。
2012年第29期(总第44期)科技视界Science &Technology VisionSCIENCE &TECHNOLOGY VISION 科技视界0引言确定地面点高程的测量工作,称为高程测量,按所使用的仪器和施测方法不同,高程测量方法主要有水准测量、三角高程测量、GPS 高程测量。
水准测量精度高,可用于任何等级的高程测量,但劳动强度大、进度慢。
全站仪三角高程测量受地形条件的限制少,具有测距精度高、测量速度快、适用范围广等特点,采用全站仪中间法三角高程测量,既可以避免量取仪器高和棱镜高所产生的误差,减少三角高程的误差来源,又有水准测量的任意设站的特点,灵活自由设站且不用对中,极大地提高了作业效率,在一定范围内可替代三四等水准测量。
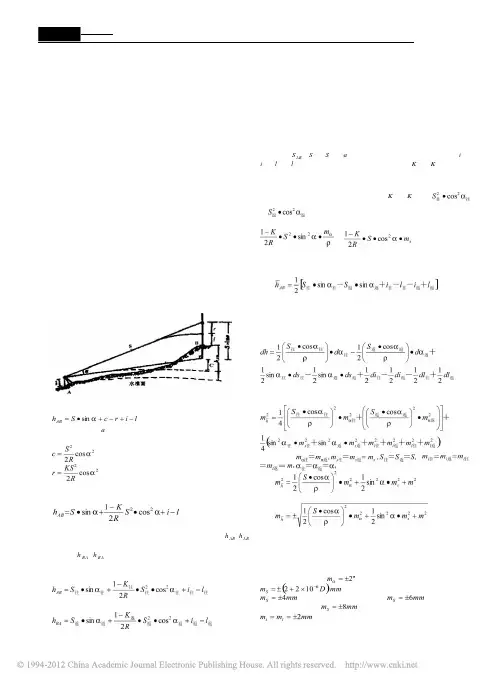
1三角高程测量的传统方法如图所示,设A,B 为地面上高度不同的两点。
已知A 点高程H A ,只要知道A 点对B 点的高差H AB 即可由H B =H A +H AB 得到B 点的高程H B 。
图1三角高程测量示意图图中:D 为A、B 两点间的水平距离,а为在A 点观测B 点时的垂直角,i 为测站点的仪器高,t 为棱镜高,H A 为A 点高程,H B 为B 点高程,V 为全站仪望远镜和棱镜之间的高差(V=Dtanа)首先我们假设A,B 两点相距不太远,可以将水准面看成水平面,也不考虑大气折光的影响。
为了确定高差hAB,可在A 点架设全站仪,在B 点竖立对中杆,观测垂直角а,并直接量取仪器高i 和棱镜高t,若A,B 两点间的水平距离为D,则hAB=V+i-t故H B =H A +Dtanа+I-t (1)或H B =H A +i+S sin α-t这就是三角高程测量的基本公式,但它是以水平面为基准面和视线成直线为前提的。
因此,只有当A,B 两点间的距离很短时,才比较准确。
当A,B 两点距离较远时,就必须考虑地球曲率和大气折光的影响(当两点距离大于300m 时,须加球气差改正数,或采用对向观测后取平均高差的方法,抵消球气差的影响)。
工程水平测量之全站仪全站仪,即全站型电子测距仪,是一种集光、机、电为一体的高技术测量仪器,是集水平角、垂直角、距离(斜距、平距)、高差测量功能于一体的测绘仪器系统。
与光学经纬仪比较电子经纬仪将光学度盘换为光电扫描度盘,将人工光学测微读数代之以自动记录和显示读数,使测角操作简单化,且可避免读数误差的产生。
因其一次安置仪器就可完成该测站上全部测量工作,所以称之为全站仪。
因为用全站仪(附加棱镜)、经纬仪(附加塔尺)测量高程,是根据两点间的距离和竖直角,应用三角公式计算两点的高差,用全站仪测定高程的方法通常称为三角高程测量(或称测距高程)。
用全站仪测量高程的特点是,精度比用水准仪测量低,但是这种方法简便、灵活,受地形的限制小。
因此通常用于山区的高程测量和地形测量。
三角高程测量,一般应在一定密度的水准测量控制之下。
通常三角高程测量是高程控制测量的一种补充手段,其精度应同同等级的水准测量相同。
当我们采用全站仪(光电测距仪)进行高程测量放样时,如图2-2所示,由于全站仪的视线不都在一个水平面上,而全站仪所读读数由正负之分,在进行高程测量放样计算时,我们输入的数据必须以全站仪所读读数实际输入,设后视点BM的高程为H0,在同一测站下(全站仪的仪器高恒等),放样点的实测高程的计算公式(以下为棱镜高度保持不变的放样点高程推导公式)如下:= H0-h0 + v视线高程H视线放样点高程Hn = H-hn-v =(H0-h0 + v)+ hn-v视线= H0-h0 + hn当棱镜高度改变时,设棱镜改变后的高度相对与后视时的高度改变值为w(改变后的高度减去棱镜初始高度),则放样点的的实测高程为:Hn = H0-h0 + hn-w。
为避免误差因距离的传递,各等级的三角高程测量必须限制一次传递高程的距离。
三角高程测量路线的总长原则上可参考同等级的水准路线的长度,路线尽可能组成闭合多边形,以便对高差闭合差进行校核。
除以上介绍的基本方法外,采用全站仪测量高程中,视线高程有两种计算方法:一、若已知置站点地面高程,则视线高程为“置站点地面高程与全站仪仪器高之和”。