频率波数谱精编版
- 格式:docx
- 大小:26.20 KB
- 文档页数:11
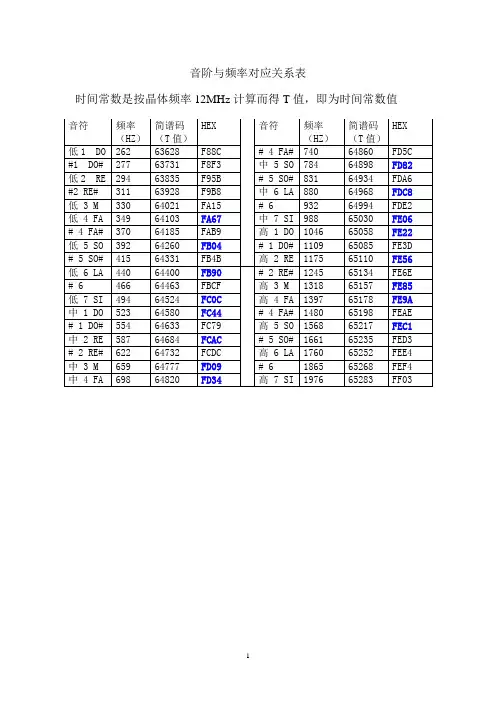
音阶与频率对应关系表时间常数是按晶体频率12MHz计算而得T值,即为时间常数值音符频率(HZ)简谱码(T值)HEX 音符频率(HZ)简谱码(T值)HEX低1 DO 262 63628 F88C # 4 FA# 740 64860 FD5C #1 DO# 277 63731 F8F3 中 5 SO 784 64898 FD82 低2 RE 294 63835 F95B # 5 SO# 831 64934 FDA6 #2 RE# 311 63928 F9B8 中 6 LA 880 64968 FDC8 低 3 M 330 64021 FA15 # 6 932 64994 FDE2 低 4 FA 349 64103 FA67 中 7 SI 988 65030 FE06 # 4 FA# 370 64185 FAB9 高 1 DO 1046 65058 FE22 低 5 SO 392 64260 FB04 # 1 DO# 1109 65085 FE3D # 5 SO# 415 64331 FB4B 高 2 RE 1175 65110 FE56 低 6 LA 440 64400 FB90 # 2 RE# 1245 65134 FE6E # 6 466 64463 FBCF 高 3 M 1318 65157 FE85 低 7 SI 494 64524 FC0C 高 4 FA 1397 65178 FE9A 中 1 DO 523 64580 FC44 # 4 FA# 1480 65198 FEAE # 1 DO# 554 64633 FC79 高 5 SO 1568 65217 FEC1 中 2 RE 587 64684 FCAC # 5 SO# 1661 65235 FED3 # 2 RE# 622 64732 FCDC 高 6 LA 1760 65252 FEE4 中 3 M 659 64777 FD09 # 6 1865 65268 FEF4 中 4 FA 698 64820 FD34 高 7 SI 1976 65283 FF03频率简谱码频率简谱码低F88C # 4 FA# FD5C 音符 (HZ ) (T 值) HEX 音符 (HZ ) (T 值) HEX 1 DO 262 63628 740 64860 #1 DO# 277 63731 F8F3 中 5 SO 784 64898 FD82 低2 RE 294 63835 F95B # 5 SO# 831 64934 FDA6 #2 RE# 311 63928 F9B8 中 6 LA 880 64968 FDC8 低 3 M 330 64021 FA15 # 6 932 64994 FDE2 低 4 FA 349 64103 FA67 中 7 SI 988 65030 FE06 # 4 FA# 370 64185 FAB9 高 1 DO 1046 65058 FE22 低 5 SO 392 64260 FB04 # 1 DO# 1109 65085 FE3D # 5 SO# 415 64331 FB4B 高 2 RE 1175 65110 FE56 低 6 LA 440 64400 FB90 # 2 RE# 1245 65134 FE6E # 6466 64463 FBCF 高 3 M 1318 65157 FE85 低 7 SI 494 64524 FC0C 高 4 FA 1397 65178 FE9A 中 1 DO 523 64580 FC44 # 4 FA# 1480 65198 FEAE # 1 DO# 554 64633 FC79 高 5 SO 1568 65217 FEC1 中 2 RE 587 64684 FCAC # 5 SO# 1661 65235 FED3 # 2 RE# 622 64732 FCDC 高 6 LA 1760 65252 FEE4 中 3 M 659 64777 FD09 # 6 1865 65268 FEF4 中 4 FA698 64820FD34高 7 SI 1976 65283FF03机器周期Tc = 1.085μs音符频率(HZ)信号周期 T T0/Tc 时间常数X值HEX 低 4 FA 349 2865 1320 64216 FAD8 低 5 SO 392 2551 1175 64361 FB69 低 6 LA 440 2273 1047 64489 FBE9 低 7 SI 494 2024 933 64603 FC58 中 1 DO 523 1912 881 64655 FC8F 中 2 RE 587 1704 785 64751 FCEF 中 3 M 659 1517 699 64837 FD45 中 4 FA 698 1433 660 64876 FD6C 中 5 SO 784 1276 588 64948 FDB4 中 6 LA 880 1136 524 65012 FDF4 中 7 SI 988 1012 466 65070 FE2E 高 1 DO 1046 956 440 65096 FE48 高 2 RE 1175 851 392 65144 FE78 高 3 M 1318 759 350 65186 FEA2 高 4 FA 1397 716 330 65206 FEB6 高 5 SO 1568 638 294 65242 FEDA。


可见光的波长与频率对照表绿光波长为500-560nm,黄光波长为580-595nm。
不同波长的可见光所对应的不同颜色。
声波的频率范围0.0001Hz~10^12Hz以上,人耳可以听到的频率范围20Hz-20000Hz,把(20000Hz~10^12Hz以上)的声音称为超声波,把(0.0001Hz~20Hz)的声音称为次声波.可见光的波段频率范围是3.9×10^14到7.7×10^14赫兹,紫外线的波段频率范围大致在8×10^14到3×10^17赫兹之间,而红外线波长的范围大致在3×10^11到约4×10^14赫兹之间.光波是电磁波,声波是机械波.光波(即电磁波的可见光谱)的速度为每秒30万公里,声波的速度为每秒340米,人的视觉神经的传递速度为每秒1200~1400米,人的听觉神经的传递速度为每秒 800~1200米.声波与光波的更大的区别在于前者需要介质,而后者不需要.声波的多普勒效应与波源、介质及观察者三者之间的相互运动有关.而光波因为没有介质,光的多普勒效应只涉及光源与观察者之间的相对运动。
换一个角度来讲,可以说光在真空中的传播也是通过某种介质,但这种介质有一个非常特殊的性质,它相对于所有的惯性参照系的运动速度都为零.正是这个特征,使得“光速与光源的运动速度无关”与“光速与观察者的运动速度无关”等价.而声波的传播媒介(空气、水等)都不具备这种“永远静止”的性质,故不存在“声速不变原理”,也无法由此导出相对论.另外,光波也能在非真空介质(如玻璃等)中传播,但是这些介质也不具备这种“永远静止”的性质,所以也不能用光波在这类介质中的传播速度替代相对论中的光速。
可见光的色散谱根据波长依次为红、橙、黄、绿、青、蓝、紫。
对应的波长(频率)在下表中列出。
可见光的波长与频率对照表名称波长(纳米)频率(兆赫)紫光波长400~435 790-680蓝光波长450~480 680-620青光波长480~490 600-620绿光波长500~560 600-530黄光波长580~595 530-510橙光波长595~605 510-480红光波长605~700 480-405光通过材料后,其强度或多或少地会减弱,实际上就是一部分光能量被固体吸收。






电磁波谱频率电磁波谱频率是描述电磁波传播特性的物理量,它指的是电磁波的振动次数或周期在单位时间内重复的次数。
电磁波是由电场和磁场交替变化而形成的,在空间中传播并传递能量。
电磁波谱频率的范围非常广泛,从极低频到极高频都有不同的电磁波。
根据频率的不同,可以将电磁波分为以下几种:1. 无线电波:无线电波是电磁波中频率最低的一种。
它的频率范围从几十赫兹到几百千赫兹。
无线电波被广泛应用于无线通信、广播和雷达等领域。
2. 微波:微波的频率范围介于无线电波和红外线之间,大致在几百千赫兹到几百千兆赫兹之间。
微波主要应用于通信、雷达、热感应和微波炉等领域。
3. 红外线:红外线的频率范围从几百千兆赫兹到几百万千兆赫兹。
红外线是一种辐射热能的电磁波,它被广泛应用于红外线热像仪、红外线通信和安防系统等领域。
4. 可见光:可见光是人眼可见的电磁波,频率范围从几百万千兆赫兹到几百万千万千赫兹。
可见光的颜色与频率有关,包括红、橙、黄、绿、青、蓝和紫七种颜色。
可见光被广泛应用于照明、显示和光通信等领域。
5. 紫外线:紫外线的频率范围从几百万千万千赫兹到几百千兆赫兹。
紫外线有短波紫外线、中波紫外线和长波紫外线等不同类型。
紫外线具有辐射和杀菌作用,在紫外线消毒、紫外线固化和紫外线检测等领域得到广泛应用。
6. X射线:X射线的频率范围从几百千兆赫兹到几百亿千兆赫兹。
X射线具有穿透力强的特点,被广泛应用于医学影像学、材料检测和安全检查等领域。
7. γ射线:γ射线的频率范围最高,可以达到几千亿千赫兹甚至更高的频率。
γ射线是一种高能电磁辐射,用于核物理研究、医学治疗和工业无损检测等领域。
在不同的频率范围内,电磁波的特性和应用也不同。
随着频率的增加,电磁波的能量也增加,其穿透力和波长也会发生变化。
对于无线通信和数据传输来说,较高频率的电磁波具有更高的带宽和传输速率,但穿透能力较低。
而对于辐射治疗和材料检测来说,具有更高能量的γ射线则更加有效。

电磁波谱频率和波长电磁波,这个看似神秘却又无处不在的“家伙”,其实与我们的生活息息相关。
要真正了解电磁波,就不得不提到它的两个重要属性——频率和波长。
想象一下,电磁波就像是在大海中航行的波浪,而频率就是波浪起伏的快慢,波长则是两个相邻波峰或波谷之间的距离。
频率越高,意味着电磁波的能量越大;波长越短,它的穿透力可能就越强。
先来说说频率。
频率的单位是赫兹(Hz),它表示电磁波在每秒内完成周期性变化的次数。
比如,我们日常使用的无线电广播,其频率通常在几百千赫兹到几百兆赫兹之间。
而可见光的频率则要高得多,这也是为什么我们能看到五彩斑斓的世界。
不同频率的电磁波有着不同的用途。
低频率的电磁波,像长波无线电,能够传播很远的距离,甚至可以绕过一些障碍物,所以常用于远距离的通信,比如航海通信。
中频率的电磁波,比如调幅广播,能够在较大的范围内传播,为我们带来各种新闻和音乐。
高频的电磁波,比如微波炉中使用的微波,其能量较高,可以用来加热食物。
而极高频率的电磁波,如 X 射线和伽马射线,则具有很强的穿透力,在医学和科学研究中发挥着重要作用。
接下来谈谈波长。
波长和频率之间有着密切的关系,它们的乘积等于电磁波传播的速度,而在真空中,这个速度就是光速,约为 30 万公里每秒。
所以,频率越高,波长就越短;频率越低,波长就越长。
波长较长的电磁波,比如无线电波,能够绕过障碍物传播,因此适用于远程通信。
但它们的分辨率较低,难以传递精细的信息。
相比之下,波长较短的电磁波,如紫外线、X 射线和伽马射线,虽然传播距离较短,容易被物质吸收,但却具有很高的分辨率,可以用于医学成像、材料检测等领域。
再看看我们身边常见的例子。
手机通信使用的电磁波波长较短,频率较高,能够在有限的频谱资源中传输大量的数据,让我们可以快速上网、视频通话。
而卫星通信则使用波长较长的电磁波,以便覆盖更广阔的区域。
在科学研究中,对电磁波谱频率和波长的研究也具有重要意义。
天文学家通过观测来自宇宙深处的不同波长的电磁波,来探索星系的形成和演化。

信号的频率谱
信号的频率谱是信号在频率领域的表示,它描述了信号在不同频率下的幅度和相位。
对于离散信号,其频谱是离散的;对于连续信号,其频谱是连续的。
频率谱的获取通常需要对信号进行傅里叶变换,将时域信号转换到频域。
对于周期信号,频谱是一个无限长的序列,对于非周期信号,频谱是一个连续函数。
在频率谱中,幅度谱表示了信号在不同频率下的幅度,相位谱表示了信号在不同频率下的相位。
对于复杂信号,如调制信号,其频谱可能包含多个频率成分,包括基波和各次谐波。
在通信系统中,频率谱的使用非常重要,因为它可以帮助我们了解信号的频率成分,从而优化信号处理和传输效率。
频率波数谱三、频率波数域中的面波面波的各个模态,在时间和距离上往往是相互穿插叠合的。
在频率波数域中,可以清楚地区分开面波不同模态的波动能量,从而能够单一地提取出基阶模态的频散数据。
频率波数谱、相速度、谱振幅面波沿地表传播的波场,在时间和空间上都可以分解为正弦和余弦形式的波动组份,转换成二维的频谱。
单个波动组份在时间上的频度,以每秒中的波动次数来计量,就是一般称的频率(F),单位为赫芝(Hz),而在空间(距离)上的频度,以每米中的波动次数来计量,称为波数(K),单位为1/米(1/m)。
由频率波数谱中某个波动组份的频率和波数,可以确定它的周期(T = 1/F)和波长(L = 1/K)。
这个波动组份的波形在波场中传播时,每个周期的时间前进一个波长,计算出的速度就是它的传播速度(Vc = L/T, 或Vc = F/K),也称为该组份的相速度。
由波动组份正弦和余弦分量的振幅,可以合成该组份的谱振幅,反映了该组份传播的弹性能量的大小。
运用二维富里叶变换,可以将时间距离域的弹性波场数据,转换为频率波数谱数据,表现为二维座标中的图形。
一般其左上角为座标原点,纵座标为频率轴,沿纵座标向下波动频率增高,也就是在时间上波动越快。
横座标为波数轴,沿横座标向右波数增多,也就是在空间上波长越短。
各个波动组份谱振幅的大小,用不同颜色的色标来表示,一般色度越亮,表示谱振幅越大。
波动组份座标点(F,K) 和原点联线的斜率(F/K),体现了它的相速度。
这条联线越陡该波动组份的相速度越大,越缓相速度越小。
离散数据的二维富里叶变换,对于转换的频率和波数区间,都有相应的限定。
转换的频率限(Fmax)是采样时间间隔(dT)的倒数的的一半(Fmax = 0.5/dT)。
转换的波数限(Kmax)是采样道间距离(dX)的倒数的一半(Kmax=0.5/dX),对于单向传播的波场,最大波数可以扩大一倍(Kmax=1/dX)。
在频率和波数限定区间以外,会出现变换折叠造成的干扰。
面波的频率波数谱、谱能量轴层状地层上激发的面波波场数据,经过频率波数转换,其波动组份的谱振幅会形成连续的线状“山脉”,其峰值点的连线称为能量轴。
面波的弹性能量是在这些能量“山脉”所包含的频率和波数范围内传播的。
各个能量轴的波动组份合成面波波场的各个模态。
由能量轴的频率和波数值,可以计算出面波各个模态的频散特征。
左图是一个多道面波数据的频率波数谱图形。
白线长框圈出的就是基阶模态的能量轴,它的右上方没有出现显著的其他能量轴,而左下方显出的不很连续的能量轴,大都是面波高阶模态的表现。
基阶模态能量轴延续性较好,贯穿的频率和波数区间,包含了面波其他能量轴的展布范围,一般能说明地层在采集排列的区间内是层状或似层状的,而且最底层的地层刚度最强。
左图是上面谱图左上部放大的图形。
红色和白色的圆点分别标示出基阶模态和高阶模态能量轴上的两个波动组份。
它们都位于同一频率的横线上,但具有的波数值不同。
不同的波数代表不同的波长,从而相速度也有差别。
相速度的差别,可以从它们和座标原点连线的斜率看出,基阶模态红点连线的斜率缓,相速度小,白点连线的斜率陡,相速度也大。
同一频率的面波波动,会出现两种以上不同相速度(不同波长)的波动组份,是层状地层中面波具有多种传播方式(模态)造成的。
特别当地层中具有明显的软弱夹层时,构成的波导会导致出现强的高阶模态能量轴。
时间距离域窗口对频率波数谱的作用为了排除其他干扰波的影响,在作频率波数转换时,对时间距离域数据加时距窗口,也就是把窗口外的波形数据置以零值。
时距窗口的位置和边沿数据的梯度,对形成的频率波数谱都有影响。
左图显示的是以上谱图的面波采集数据记录,黄色线条圈出所用的时距窗口。
窗口包含了完整的面波波场范围。
在时间轴方向上,窗口边沿通过的数据都比较小,从而时间梯度也不会很大。
但是在空间(距离)轴方向上,由于不可能将采集道延伸到面波消失的距离,所以在采集排列的两端,不可避免地会出现空间梯度很大的数据台阶。
图中的红色箭头指向面波基阶模态出现的部位,以上谱图中白色线框圈出的谱能量轴,就是时间距离域中这个部位数据的频率波数谱。
由于它在时间及空间(特别在右部)都和上部的高阶模态数据交错叠合,很难单纯用时距窗口把它提取出来。
左图显示的是设置的另一个时距窗口,它圈出的主要是高阶模态(红色箭头)出现的部位。
窗口下边沿通过起伏很大的波形数据,预期在谱图上将出现截断台阶的效应。
下图就是用这个时距窗口作出的谱图。
左图显示的就是用以上时距窗口作出同一采集记录的谱图。
其中基本显出了以上完整谱图中高阶模态的强能量轴(红色箭头)。
同时在两旁出现了多条平行的弱能量轴(白色箭头),应属于时距窗口边沿截断不当的结果,当然也会包含记录道两端的空间截断效应。
采集道间距离对频率波数谱的影响面波的波场一般都是单向传播的。
采集数据转换成频率波数谱图,其最大波数限是道间距离的倒数。
例如:以上谱图波数轴右端的最大波数值Kmax = 0.5(1/m),就是采集道间距2(m) 的倒数。
谱图波数轴右端的最大波数,限定了谱图能够正确确定的最小面波波长,也就是采集记录的道间距。
如果把以上24 道的采集记录(道距为2m),抽取单数道,组成一个12 道的记录(道距为4m),显示如左图。
新记录转换成频率波数谱图,显示如下图。
预期谱图波数轴右端的最大波数,将是原来24 道记录谱图的一半,可以确定的最小面波波长,将扩大成原来谱图的一倍。
左图为12 道新记录的频率波数谱图。
它可以确定的最大波数为0.25(1/m) ,显示在波数轴的右端(最小面波波长为4m)。
比这个波数限更大波数(更小波长) 的面波波动组份的谱能量,会在波谱转换中折叠到波数轴的左端。
图中显示由左上延伸向右下的基态面波能量轴,在波数轴上的跨度比波数限更宽。
它在波数轴右端被截断(红色箭头所指处),而它的延伸部分,被折叠到谱图同一频率座标(白色横线)的波数轴的左端(黄色箭头所指处),并向右延伸成为虚假的低波数能量轴。
这种由于采集道间距过大造成的波数谱折叠,在区分面波的各个模态时会产生误会,应予识别和排除。
采集道排列长度对频率波数谱的影响频率波数谱能够确定的面波最大波长(Lmax),不能大于采集通道排列跨距(排列道数乘以道间距)的两倍。
这个最大波长的倒数,决定了波数谱能够确定的最小波数值,也是谱图波数分辨能力的限度。
采集排列越长,谱图能正确反映的面波波长越长,区分不同面波波长的能力越强,与此同时,排列两端的空间数据截断对谱图的影响也越弱。
左图是24 道采集记录的谱图。
道间距为2m,排列跨距为48m,对应的最小波数值为0.0104(1/m),以白色的垂直线表示在谱图的左方。
白色箭头指出的是两端道数据空间截断产生的能量轴。
由于排列长度比较大,面波的各个能量轴都比较窄,空间截断效应也比较弱,从而各个模态能量轴的区分比较明显。
左图是24 道记录取中间12 道所作的谱图。
道间距仍为2m,排列跨距缩短为24m,对应的最小波数值为0.0208(1/m),也以白色的垂直线表示在谱图的左方。
白色箭头指出的仍是两端道数据空间截断产生的能量轴。
由于排列长度缩短,面波的能量轴都变宽,空间截断效应变强,各个模态能量轴的区分也变差。
左图是24 道记录取中间 6 道所作的谱图。
道间距仍为2m,排列跨距缩短为12m,对应的最小波数值为0.0417(1/m),仍以白色的垂直线表示在谱图的左方。
白色箭头指出的仍是两端道数据空间截断产生的能量轴。
由于排列长度更加缩短,面波的能量轴变得更宽,空间截断效应更强,各个模态能量轴的区分也相应变得更加模糊。
以上三个不同采集排列长度的谱图左方的三条波数限度线,同时也是相应采集排列的谱图能够可靠确定的面波波长的上限。
在它们左方的谱图中,能量轴表现出的波数和频率数值,只能是转换中的外推结果,已经不会有充分的时间距离域原始数据作为依据。
面波的频率波数谱向低频小波数(长波长)区延伸的表现在频率波数谱的左上角,频率降低、波数减小,反映大深度的长波长面波应该在这个区域内分布。
但正就是在这个区域,波谱对不同类型波的相对分辨能力降低,如果基阶面波不具备较强的能量峰脊,就很难提取到正确的频散数据。
下图显示了在频率波数谱左上角经常遇到的图景:左图是一个实测的面波记录的频率波数谱上,阴影圈定了明显的基阶面波的能量峰,其中白色点标记出峰脊的位置。
在反映低频长波长的左上方(红框内),分布着一些弱的能量轴,难以作出明确的选择,可靠的频散数据低频端只能到此为止。
了解基阶面波能量峰向频率波数谱左上角延伸的一般规律,将有利于识别和提取频散数据。
为此,我们在这个面波记录的频率波数谱上,标上由它得到的地层模型正演的基阶和高阶频散数据点,并且正演了原来未拾取到的左上角低频频散数据点,一并显示如下图:……………………………………………………………最新资料推荐…………………………………………………左图是标上了正演得到的频散数据点的实测记录频率波数谱图形。
其中白色点组成的线是正演的基阶频散数据,淡灰色点组成的两条线属正演的高阶频散数据。
它们的中下部均能和谱图中相应的能量峰脊相吻合,说明正演采用的地层模型正确地反映了这部分谱图的面波能量。
正演基阶频散数据线向左上方的延伸部分逐渐逼近频率波数座标的原点,这就是基阶面波能量峰脊向低频小波数(长波长)区延伸的方向。
图中还以红色直线标出地层最大剪切波速(底层)在频率波数谱中反映的位置,在此红线左方出现的能量峰,其相速度都大于地层底层的波速,不属于面波能量的表现。
11。