三年级下数学教学设计面积的估测_沪教版

树叶的面积教学目标：1. 知识目标：能用数方格的方法估测出不规则平面图形的面积。

2. 能力目标：通过让学生亲身经历估测活动的过程，初步体会“四舍五入”的思想方法，发展学生的空间观念。

3. 情感目标：激励学生大胆思考、积极主动发表自己的见解，并能与同学交流探讨，分享解决问题的快乐。

教学重点：体验用一个标准的方格（面积单位）来进行测量的必要性。

教学难点：判断哪些格子“小于半格的可以舍去，大于等于半格的算一格”。

教学准备：课件、透明厘米方格纸教学过程：一、比较引入出示课件：上海的秋天师：秋天一到，上海的许多树的树叶飘落了，今天我们数学课也来研究这树叶。

研究树叶的什么呢？——板书：树叶的面积师：先指一指树叶的面积是哪一部分？（拿出事先准备的树叶摸一摸，指一指）师：求这片树叶的面积，你们发现与上学期学习图形的面积时有什么不同？（上学期所学的平面图形是规则的图形。

有的能通过公式进行计算，像长方形、正方形。

有的能通过用方格数出来。

这片树叶的周围是凹凸不平的。

）师：（课件出示：一片树叶）它是一个不规则的图形，面积如何算呢？这就是今天我们一起来研究的内容。

[通过让学生比较，不仅再现上学期求平面图形面积时的方法，而且发现今天所学图形的形状是不规则的，激发学生的求知欲望，探索知识的兴趣。

]二、探索新知1. 师：这一片树叶的面积有多大？每一个同学积极思考、大胆猜想，以小组为单位进行思考。

（可以用厘米透明方格纸来计数……）全班讨论哪一种方法好，为什么？师：还是要用一个统一的标准的方格进行计数。

（课件演示：在树叶上摆放透明的厘米方格纸），发现出现了一些什么情况？（树叶有的在透明的厘米方格纸中，出现了满格、半格，还出现了大于半格和小于半格的情况。

）师：观察得真仔细！（课件出示）先来数一下整格的：31格。

余下的怎么办？（可以把少的与多的拼在一起算一格；可以……，请学生大胆思考，畅所欲言，积极发表自己的见解。

）师：生活中我们可以大于等于半格的算一格，小于半格的可以舍去不算。

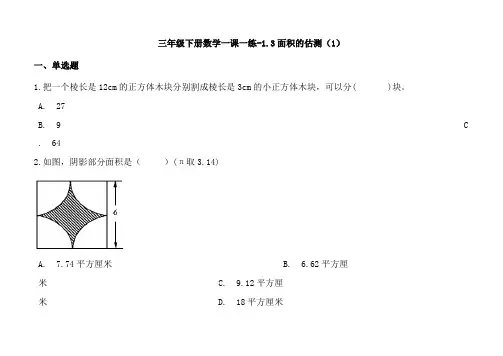
三年级下册数学一课一练-1.3面积的估测（1）一、单选题1.把一个棱长是12cm的正方体木块分别割成棱长是3cm的小正方体木块，可以分( )块。

A. 27B. 9 C . 642.如图，阴影部分面积是（）(π取3.14)A. 7.74平方厘米B. 6.62平方厘米 C. 9.12平方厘米 D. 18平方厘米3.如图，图中圆的半径为r，长方形的长为2r，图中甲乙两块阴影部分的面积相比较，( )。

A. 甲的面积大B. 乙的面积大 C. 一样大 D. 无法比较4.用一张长8厘米，宽6厘米的长方形剪出一些边长为3厘米的正方形，最多能剪（）个．A. 2 B . 4C. 65.求图中阴影部分的面积是（）平方厘米．A. 28.5B. 31.4C. 36D. 42.56.把棱长是6cm的正方体切成棱长是1cm的小正方体，可切（）块．A. 216B.36 C . 6二、判断题7.计算组合图形的面积也要用到基本图形的面积公式。

8.将100个棱长1cm的小正方体拼在一起，无论怎样拼，拼出的图形的体积都是100cm2．．（判断对错）9.下面两图中阴影部分的面积相等。

(每个小方格的边长表示1cm)10.右图中的阴影部分面积占长方形的。

三、填空题11.数一数，填一填。

(每个小方格的面积表示1平方厘米)________________________12.估一估，下面每个图形所占的面积大约是多少？(每个小方格的面积表示1cm2)________13.下面是阳阳设计的运动场图纸．这个运动场有8条跑道，在图纸上每条跑道宽0.122cm，最里侧半圆跑道的直径为3.6cm，直跑道长9.6cm．比例尺： 1 ∶ 1 000 ．回答下列问题．（1）这个运动场的占地面积是________平方米？(得数保留整平方米)（2）如果要给这个运动场铺上15cm厚的沙子，需要沙子________立方米？（3）如果要给8条跑道和排球场地上铺设塑胶，每平方米价格是170元，一共要用________钱？(保留整数) （4）弯道面积是________平方米？(保留整数)14.用不同的方法计算下图的面积________．(单位：厘米)15.计算下面图形的面积________．(单位：厘米)四、计算题16.先量一量，再计算下面图形的面积。

估测图形的面积教学内容：小学数学三年级下册第54页教学目标1.进一步感知面积单位平方厘米、平方分米、平方米的大小，能自选单位正确估计不规则的图形面积的大小，能用数方格的方法计算一些不规则图形的面积，初步体会“四舍五入”的思想方法。

2.能借助方格图估算不规则图形的面积，在估算面积的过程中，体验解决问题策略的多样性，培养初步的估算意识和估算习惯，体验估算的必要性和重要作用。

3.通过学生参与教学，培养学生的观察、分析、归纳能力及学生的分组讨论、合作探究，培养学生合作学习的意识和能力。

4.经历观察、估计、测量图形的面积的过程，进一步发展学生的空间观念。

5.在估测图形的面积的过程中，体会数学与现实生活的密切联系，感受数学的应用价值。

教学重难点教学重点：能用数方格的方法估测出不规则平面图形得面积；初步体会“四舍五入”的思想方法。

教学难点：经历观察、估测、归纳等探索物体和图形大小的过程。

教具、学具多媒体课件、方格纸、1平方厘米和1平方分米纸片。

教学过程一、创设情境，提出问题1.情景：同学们，上节课我们学习了面积和面积单位，谁来说一说常用的面积单位有哪些？（平方米、平方分米、平方厘米）谁举例说明1平方米、1平方分米、1平方厘米有多大？生活中有的图形是不规则的，今天我们就来学习怎样估测图形的面积。

板书课题：估测图形的面积出示情境图：星期天,小丁丁、小胖、小亚和小巧组织的雏鹰假日小队活动，一起到森林公园去游玩，他们看到树林里的草地上有些树叶，他们会提什么问题呢？一片树叶的面积有多大？一片树叶到底有多大呢?今天我们来学习树叶的面积。

1、能用数方格的方法估测出不规则平面图形的面积。

初步体会“四舍五入”的思想方法。

2、通过学生参与教学，培养学生的观察、分析、归纳能力。

3、通过分组讨论、合作探究，培养学生合作学习的意识和能力。

师： 这片树叶的面积是多少呢？同学们，你们可以帮助他们 吗？学生交流后师总结：对呀！我们必须用一个标准的方格来测量。

面积计算教学目标：1. 知识目标：能通过观察，弄清图形的组合关系。

2. 能力目标：通过割、补的方法，求出组合图形的面积。

3. 情感目标：培养学生观察问题，分析问题的能力。

教学重点：能通过割、补的方法，求出组合图形的面积。

教学难点：能通过观察，弄清图形的组合关系。

教学过程：一、情景引入1．你能算出小巧卧室和书房各占地面积有多大吗？（单位：米）生：①8x4=32（m2），②5x5=25（m2）。

2. 师：两个房间总占地面积是多少？生：32+25=57（m2）3. 师：今天我们继续来学习面积的计算。

揭示课题：面积的计算二、探究学习1.2. 生小组讨论，尝试计算。

3. 交流：（1） 4×9+15×5=36+75=111m2（2） 9×9+6×5=81+30=111m2（3） 9×15-6×4=135-24=111m2（4）可能会出现的情况9×4+5×9+6×5=36+45+30=111m24. 教师小结：同学们通过分割【如方法（1）（2）（4）】，可以把这个不规则图形变成我们认识的长方形、正方形这两个基本图形。

这样我们就能计算出面积了。

（板书：分割）还有的同学将原图形“补”一块，使之成为基本图形。

用补出的大图形减去填补的小图形也能求出原来图形的面积。

（板书：补）比较，你喜欢哪种方法？（如学生中出现方法4，可通过比较，让学生明白分成两个图形能解决问题就不要分成三个图形去计算。

）三、巩固练习1. 模仿练习：求出小亚的卧室占地面积。

（小亚卧室）问：三个人谁的卧室最大？谁的最小？2.学生先独立做，再交流。

三年级数学下册1.5《面积计算》教案4沪教版教学目标：1. 知识目标：（1）通过观察、分析，弄清图形的组合关系。

（2）通过割、补的方法，求组合图形的面积。

2. 能力目标：通过实践操作，培养学生观察、分析以及合理解决问题的能力。

3. 情感目标：在运用数学知识解决实际问题的过程中，让学生体验到成功的乐趣，体会数学的价值。

教学重点：能正确合理地求组合图形的面积。

教学难点：弄清图形的组合关系，准确判断分割后图形的尺寸。

教学准备：简单图形的纸片、剪刀、多媒体课件。

教学过程：一、复习1. 课件出示：长方形和正方形。

师：这是我们学过的长方形和正方形。

师：现在要求它们的面积必须知道什么呢？生：要知道长方形的长和宽，以及正方形的边长。

2. 标上相应尺寸。

师：求图形的面积必须要有相应的尺寸，请看！课件出示：10dm5dm师：现在能算了吗？左右同学各口算一题。

生汇报：长方形的面积=长×宽=10×5=50（dm2）正方形的面积=边长×边长=4×4=16（dm2）[复习长方形、正方形的面积的计算公式，为求组合图形的面积作铺垫，同时让学生体会求图形的面积必须知道相应的尺寸。

]二、探究1. 把引入部分的长方形和正方形合二为一。

课件出示：师：这个图形是由我们学过的图形组合而成的，这样的图形叫组合图形。

（出示部分课题：组合图形）2. 课件出示一些组合图形。

①②③让学生仔细观察图形的特点后，以小组为单位互相说说它们是由哪些图形组合而成的，然后汇报。

图①图②图③学生可能有其它想法，教师根据学生汇报后小结。

3．小结：1)组合图形的组合关系，可以是几个图形的“和”（一般用“割”的方法）。

也可以是几个图形的“差”（一般用“补”的方法）。

2)图形的组合关系，由于观察、分析思考的方法不同，可以有不同的组合关系。

[这一层次设计，让学生弄清图形的组合关系，学会一般的“割”“补”方法，为后一层次找相应尺寸，计算面积作铺垫。

1.3《面积的估测》教学设计1.3《面积的估测》教学设计
徐汇区园南小学龚海英
教学目标：
1
1
2
1
1
2
教学过程：
教学过程：
一复习导入
1、计算下面图形的面积（口答）
【说明：通过复习回忆得出如果是简单图形，如长方形、正方形、平行四边形、三角形、梯形就可以用面积公式求面积。

】
二、探究新知：
1、你知道下面图形的面积吗？
今天我们来探究不规则图形《面积的估测》
2.
(
3.
(2)
(3)
5
角形的面积差不多，可以通过计算三角形的面积近似地得出这个不规则图形的面积。

) （重点让学生找出三角形三个顶点的位置，以及三角形的底和高的长度）
(1)把这个图形近似地看作三角形来估测它的面积.
(2)计算这个三角形的面积是:
10×7÷2=35cm2
(3)估测结果:这个图形的面积大约是:35cm2.
6、比较这两种方法：
(1)这两种方法所得到的结果往往会不一样.
(2)第二种方法使用的是新的估测方法,所需要的条件：通过将图形近似地看作可求面积的多边形，从而对不规则图形的面积进行估测，这种方法适用于某些不规则图形与已经学习过的可求面积
5
6
1.
1
2、用你喜欢的方法估测下面的图形的面积。

3、估测下面的图形的面积。

四、课堂小结
估测不规则图形的面积时，我们可以根据图形的的特点近似看作一个或几个简单图形，运用面积公式，估测出它的面积。

五、课堂作业：练习册P3A3,B级。

第一部分本册教材概述一、教学内容与要求(一)关于《课标》的相关内容与要求本册教材涉及《上海市中小学数学课程标准》中“基本内容”的“数与运算”、“图形与几何”、“数据整理与概率统计”的部分内容，“拓展内容”的“计算工具的发展”、“长方形周长与面积的最大值与最小值”、“平面组合图形的面积”等内容，及“专题研究与实践”的“物体周长的估计、测量与计算”等内容，《上海市中小学数学课程标准》对本册教材相关内容的要求如下：1．基本内容数与运算图形与几何数据整理与概率统计2．拓展内容拓展1（二）本册教材的具体内容1．基本内容（1）数与运算①小复习（课本第2页）②带小括号的四则运算（课本第3页）③用两位数乘除（课本第8~37页）④分数的初步认识（一）（课本第41~50页）⑤计算器（课本第53页）⑥使用计算器计算（课本第54~57页）⑦乘与除（课本第66~68页）⑧分数（课本第69页）“用两位数乘除”部分包括“速度、时间、路程”、“用两位数乘”、“用两位数除”等内容。

“用两位数乘”的主要内容有：整十数乘两位数和两位数乘两、三位数。

整十数乘两位数是两位数乘两、三位数的基础，也是估算的基础，为学生探索两位数乘两、三位数的笔算方法做好必要的准备；两位数乘两、三位数通过让学生亲身经历两位数乘两、三位数的计算过程，培养学生的迁移能力和探究能力；教材在安排乘法计算的同时，还提倡学生在乘法计算前先对乘出的积进行估计，促进学生计算能力的提高，培养他们良好的计算习惯。

“用两位数除”的关键是试商，因此教材分三个层次编排：整十数除两、三位数，两位数除两、三位数，两位数除多位数。

通过生动的情景及具体操作活动，探索除数是两位数除法的计算方法，在对除数是两位数除法试商方法的探究过程中，培养学生的算法思维。

“分数的初步认识（一）”这个单元的教学内容是通过“分蛋糕”、“分纸带”、“分糖果…”等活动，直观认识“几分之一”，初步认识分数单位；由“几分之一”的累积来认识“几分之几”，初步认识分数的概念。

面积计算
教学目标：
1. 知识目标：
复习长方形与正方形面积计算方法。

2. 能力目标：
能通过观察弄清图形之间的组合关系，能运用割补法求组合图形的面积。

3. 情感目标：
培养学生观察问题，分析问题的能力。

教学重点：
能运用割补法求组合图形的面积。

教学难点：
正确选择数据计算图形面积。

教学准备：
多媒体课件。

教学过程：
一、导入
师：草坪上有很多小朋友在玩，看看这两块草坪分别是什么形状？你能算算它们的面积吗？
5m 4m
5m 6m
长方形面积=长×宽
正方形面积=边长×边长
二、中心
师：穿过这两块草坪，我们来到了游乐场，看有很多的小伙伴！游乐场的草坪是什么形状呢？你有什么方法可以计算它的面积吗？
1)学生独立思考并计算。

2)组内讨论交流方法。

3)全班汇报交流。

方法一：方法二：方法三：方法四：
小结：计算组合图形面积时，我们可以采用割或补的方法。

将复杂的图形分割成简单图形的和或差进行计算。

讨论：对于以上的四种方法，你喜欢哪种？不喜欢哪一种？为什么？
结论：用割补法计算组合图形面积时，要注意分割出的图形不宜过多，尽可能分割出少的图形进行计算。

三、练习
计算下列组合图形的面积（单位：厘米）
2
四、小结：
今天你学会了什么本领？。

树叶的面积
教学目标：
1. 知识目标：
能用数方格的方法估测出不规则平面图形的面积。

2. 能力目标：
初步体会“四舍五入”的思想方法。

3. 情感目标：
让学生亲身经历估测活动的过程，发展学生的空间观念。

教学重点：
会用数方格的方法估测不规则平面图形的面积。

教学难点：
会用“四舍五入”的思想方法处理非满格的格子。

教学准备：
树叶、透明方格纸
教学过程：
一、导入
师：你知道这个图形的面积是多大吗？用什么方法？
生讨论：先数满格5格，再用拼凑法得出剩下的格共7格，面积是7平方厘米。

（1格表示1平方厘米）。

师：可是小胖和小巧在公园里玩时，小胖对落叶产生了兴趣，问大家，一片树叶的面积有多大？
二、中心
1. 生讨论：可以用透明方格纸方在树叶上进行测量。

每一格面积是1平方厘米，先数出满格，在数剩下的，可以求出面积。

师：树叶的边是不规则的，可不像我们刚才求的那个图形的边是直边，可以用拼凑法，该怎么办呢？
生讨论：大于等于半格的算1格，小于半格的可以舍去。

2. 生完成书P4，求出一片树叶的面积。

交流；整格31格，大于等于半格共17格，树叶的面积大约是48平方厘米。

3. 同桌两人，拿出准备的叶片，动手操作，测量一片树叶的面积大约是多少？
三、小结
师：今天你学到了什么？。