同底数幂的乘法
- 格式:doc
- 大小:84.50 KB
- 文档页数:4


同底数幂的乘法公式首先,我们先明确一些基本概念和符号:- 底数(base):指数运算中的下标数字,表示要进行乘方运算的数字。
- 幂(exponent):指数运算中的上标数字,表示底数要进行的乘方运算的次数。
- 乘法(multiplication):基本数学运算,两个数相乘得到的结果。
a^m*a^n=a^(m+n)其中,a表示底数,m和n表示指数。
这个公式表明,如果两个数的底数相同,那么它们的乘积可以表示为同一个底数的幂,其指数等于两个数的指数之和。
这个公式可以通过以下步骤来证明:假设有两个数a^m和a^n,它们的底数相同,我们可以将它们相乘:a^m*a^n=(a*a*...*a)*(a*a*...*a)其中,a*a*...*a表示连乘m次a,有m个a相乘。
通过乘法的交换律,我们可以重新排列乘积的顺序:a^m*a^n=(a*a*...*a)*(a*a*...*a)=(a*a*...*a*a*a*...*a)两个连乘可以合并成一个连乘,得到:a^m*a^n=a^(m+n)这个证明说明了同底数幂的乘法公式的成立。
举一个例子来说明这个公式的应用:假设有一个数2^3*2^5,根据同底数幂的乘法公式,我们可以将它们相乘并将指数相加:2^3*2^5=2^(3+5)=2^8因此,2^3*2^5=2^8利用同底数幂的乘法公式,我们可以将乘法运算简化为指数运算,从而更容易计算和处理。
-`(a^m)^n=a^(m*n)`:指数的指数等于底数的指数的乘积。
-`a^(-m)=1/(a^m)`:负指数等于底数的倒数的正指数。
-`a^0=1`:任何数的零次方等于1这些性质和公式可以进一步扩展和应用,帮助我们处理更加复杂的指数运算和代数表达式。
总结起来,同底数幂的乘法公式是一个非常有用的数学工具,它可以将乘法运算简化为指数运算,并且可以帮助我们处理复杂的指数表达式。
同底数幂的乘法公式是指当两个数的底数相同时,它们的乘积可以表示为同一个底数的幂,其指数等于两个数的指数之和。

同底数幂相乘的法则
同底数幂是数学术语,它指的是当两个数字的幂都以同一个基数建立时,它们会相乘而不是相加。
这个法则早就被发现,它不仅有助于学生对数学基本概念的理解,同时也有助于开发出有效的解算方法。
这个法则很容易理解,它可以用计算机中的幂表示为:x x m = (x * m)。
样,这个法则也可以用加减乘除的形式表达:x/ m = (x/m) 。
同底数的幂乘法的最重要的优势在于它可以节省计算时间。
如果对两个数进行加减乘除的算术运算,那么就需要一系列步骤,而同底数的幂乘法只需要一步即可完成。
此外,同底数的幂乘法还可以用于看上去很复杂的问题,但只要运用这个法则,就能够很容易和简单地解决它们。
推广开来,同底数的幂乘法也可以用于解决复杂的数学问题,如解决方程,寻找函数的极值,求解多项式的值等等,甚至可以用于实际的工程问题。
由于同底数的幂乘法的优势,它已经被广泛用于科学计算,现代计算机也都采用了这种法则。
它还被应用于金融市场,用来计算未来投资行为的预期回报,通过它可以预测风险和投资收益,也可以用来分析未来股市走势。
同底数的幂乘法应用广泛,它不仅可以用于学校里学生的学习,也可以用于实际工程问题的求解。
它能够节省计算时间和成本,极大地提高计算效率,是一个很重要的数学工具。
综上所述,同底数的幂乘法是一个十分重要的数学工具,可以节
省计算时间和成本,从而极大的提高计算效率。
它可以用来解决学校里的学习问题,也可以用于实际工程等领域问题的解算,是一种值得赞赏的数学工具。

《同底数幂的乘法》教学案例(精选4篇)《同底数幂的乘法》教学案例篇1[课题]义务教育课程标准试验教科书数学(北师大)七班级下册第一章第3节一、教学目的:1、在肯定的情境中,经受探究同底数幂的乘法运算性质的过程,进一步体会幂的意义,进展推理力量和有条理的表达力量。
2、了解同底数幂的乘法运算性质,并能把解决一些简洁的实际问题。
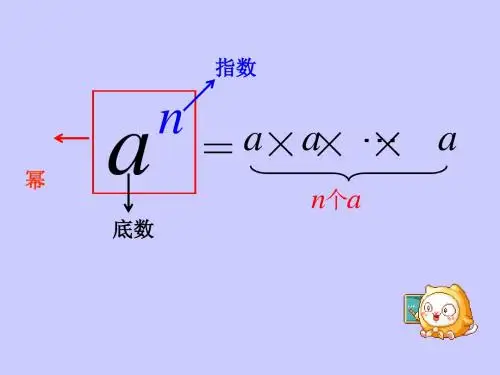
二、教学过程实录:(铃响,上课)老师:在an这个表达式中,a是什么?n是什么?当an作为运算时,又读作什么?同学:a是底数,n是指数,an又读作a的n次幂。
老师:(多媒体投影出示习题)用学过的学问做下面的习题,在做题的过程中,仔细观看,乐观思索,相互讨论,看看能发觉什么。
计算:(1) 22 × 23 (2) 54×53(3) (-3)2 × (-3)2 (4) (2/3)2×(2/3)4(5) (- 1/2)3 × (- 1/2)4 (6) 103×104(7) 2m × 2n (8)(1/7)m×(1/7)n (m,n是正整数)(同学开头做题,相互讨论、争论,气氛热闹,老师巡察、教导,待同学充分争论有所发觉后,提问有何发觉)同学A:依据乘方的意义,可以得到:(1) 22 × 23 = 25(2) 54 × 53 =57(3) (-3)2 × (-3)2 = (-3)5……老师:刚才A同学说出了依据乘方的意义计算上面各题所得结果,计算是否精确?同学:计算精确。
老师:通过刚才的计算和讨论,发觉什么规律性的结论了吗?同学 B:不管底数是什么数,只要底数相同,结果就是指数相加。
老师:请你举例说明。
同学B到前边黑板上板书:22×23=(2×2)×(2×2×2)=2×2×2×2×2=25底数不变,指数2+3=5老师:其他几个题是否也有这样的规律呢?特殊是后两个?同学:都有这样的规律。

同底数幂相乘的法则
同底数幂相乘的法则:同底数幂相乘,底数不变,指数相加。
首先,从法则来看,关键是确定底数是否相同,相同的话,就可以直接进行指数相加。
因此在做同底数幂的乘法时,分析底数是我们必须要做的工作。
底数分析一般有两种情况:第一种情况都是乘法方的形式,底数互为相反数。
在这种情况下,我们需要借助“-1的n次方,对n的奇偶性的判定”来确定整体的一个正负,从而把运算转化成同底数幂的乘法,再借助法则完成计算;第二种情况是底数有乘方关系或者都是某个数的乘方时,我们先把不是乘方形式的数转化成乘方,再判断是不是同底数,最后按照法则进行计算。
无论底数是哪一种情况,我们都需要把能化成同底数的数给化简出来,再进行计算。
其次,法则的逆用。
我们通过同底数幂的乘法法则知道同底数幂的结果的指数是通过求和得来的,那么反过来,我们就可以去求另一个因数的指数。
知道了这些以后,为我们以后解题又提供了一种解题方法。

同底数幂的乘方幂数是指在数学中,对一个数进行连乘运算的次数,也就是指数部分。
而底数则是指乘方运算的基数,也就是底数部分。
本文将详细讨论同底数幂的乘方,并探究其特性和运算规则,以便更好地理解和应用乘方运算。
1. 同底数幂的定义同底数幂指底数相同、指数不同的幂。
比如,对于底数a和指数m、n,a的m次方和a的n次方就是同底数幂。
具体表示为:a^m和a^n。
2. 同底数幂的运算规则同底数幂的运算规则有以下几个重要性质:a. 幂的乘法法则对于同底数的乘方运算,指数相加即可,即a^m * a^n = a^(m+n)。
例如,2^3 * 2^4 = 2^(3+4) = 2^7。
b. 幂的除法法则对于同底数的除法运算,指数相减即可,即a^m / a^n = a^(m-n)。
例如,5^6 / 5^3 = 5^(6-3) = 5^3。
c. 幂的乘方法则对于同底数的乘方运算,底数不变,指数相乘即可,即(a^m)^n =a^(m*n)。
例如,(3^2)^4 = 3^(2*4) = 3^8。
为了更好地理解同底数幂的运算,我们来看一些具体的实例。
a. 例子1:2^4 * 2^5根据乘法法则,我们可以将指数相加,得到2^(4+5) = 2^9 = 512。
因此,2^4 * 2^5 = 512。
b. 例子2:5^7 / 5^4根据除法法则,我们可以将指数相减,得到5^(7-4) = 5^3 = 125。
因此,5^7 / 5^4 = 125。
c. 例子3:(4^3)^2根据乘方法则,我们可以将指数相乘,得到4^(3*2) = 4^6 = 4096。
因此,(4^3)^2 = 4096。
通过以上实例可以发现,同底数幂的乘方运算可以简化为对指数的运算,从而使得复杂的计算变得更加简便。
4. 同底数幂的应用同底数幂在数学和实际生活中有着广泛的应用。
以下是一些常见的应用场景:a. 科学计算在科学领域中,同底数幂的乘方运算是常见的数学操作。
例如,在物理学中,计算物体的能量、功率等都涉及到幂数运算。

同底数幂的乘法典型题同底数幂的乘法是指当底数相同时,指数相加的运算规则。
在数学中,同底数幂的乘法是非常常见的题型,它在代数运算中扮演着重要的角色。
我们来看一个简单的例子:计算2的3次方乘以2的4次方。
根据同底数幂的乘法规则,我们可以将底数相同的幂相加。
所以,2的3次方乘以2的4次方等于2的(3+4)次方,即2的7次方。
通过计算,我们可以得到2的7次方等于128。
这个例子清楚地展示了同底数幂的乘法规则。
同底数幂的乘法也可以用代数式来表示。
如果我们有两个数a和b,并且它们的底数相同,那么a的m次方乘以a的n次方等于a的(m+n)次方。
这个规则可以推广到任意个数的乘法。
例如,a的m 次方乘以a的n次方乘以a的p次方等于a的(m+n+p)次方。
这个规则在解决代数问题时非常有用。
在实际应用中,同底数幂的乘法常常用来简化计算。
例如,在科学计算、工程设计以及金融领域等等,同底数幂的乘法可以帮助我们快速计算复杂的表达式。
通过运用同底数幂的乘法规则,我们可以将复杂的问题转化为简单的乘法运算,提高计算效率。
除了同底数幂的乘法,指数运算还包括同底数幂的除法和幂的幂等运算。
同底数幂的除法是指当底数相同时,指数相减的运算规则。
例如,2的5次方除以2的3次方等于2的(5-3)次方,即2的2次方。
幂的幂等运算是指当进行多次幂运算时,指数相乘的运算规则。
例如,(2的3次方)的4次方等于2的(3*4)次方,即2的12次方。
同底数幂的乘法在数学中有着广泛的应用。
它不仅在代数运算中起到重要作用,还在其他数学分支如几何学、概率论和数论中发挥着重要的作用。
对于学习数学的学生来说,掌握同底数幂的乘法规则是非常重要的基础知识。
总结起来,同底数幂的乘法是指当底数相同时,将指数相加的运算规则。
它在数学中扮演着重要的角色,用于简化计算、解决代数问题以及应用于其他数学分支。
同底数幂的乘法规则可以通过数学表达式来表示,也可以通过具体的例子进行理解。
掌握同底数幂的乘法规则是数学学习中的基础知识,对于提高计算效率和解决实际问题具有重要意义。

人教版同底数幂的乘法同底数幂的乘法是数学中的一个重要概念,常常在代数运算中会遇到。
在人教版的教材中,同底数幂的乘法是初中数学知识的一部分,旨在帮助学生理解指数、幂和乘法运算的关系。
以下是我为你准备的内容:一、同底数幂的概念和性质同底数幂的概念是指具有相同底数的幂,在进行相乘运算时,底数不变,指数相加。
例如,对于底数为a的两个幂a^m和a^n,它们的乘积可以用同底数幂的性质表示为a^m * a^n = a^(m+n)。
这个性质使得我们能够简化复杂的乘法计算,降低运算的难度。
二、同底数幂的乘法计算方法为了更好地理解同底数幂的乘法,我们可以通过具体的计算示例来进行说明。
考虑以下例子:例1:计算2^3 * 2^4。
解:根据同底数幂的乘法性质,我们可以将这两个幂的指数相加,即2^(3+4) = 2^7。
例2:计算10^2 * 10^(-1)。
解:同样地,我们可以将这两个幂的指数相加,即10^(2+(-1)) = 10^1 = 10。
例3:计算3^(-2) * 3^(-3)。
解:同底数幂的乘法性质同样适用于负指数的情况,所以我们可以将这两个幂的指数相加,即3^(-2) * 3^(-3) = 3^(-2-3) = 3^(-5)。
通过这些例子,我们可以看到,在进行同底数幂的乘法运算时,我们只需要将底数保持不变,将指数相加即可得到结果。
三、同底数幂的乘法规律除了上述的同底数幂的乘法性质之外,还有一些其他的规律可以帮助我们更好地理解和运用同底数幂的乘法。
规律1:对于任意非零实数a,a^0 = 1。
这个规律告诉我们,任何非零实数的0次幂都等于1。
例如,2^0 = 1,3^0 = 1,10^0 = 1等等。
规律2:对于任意非零实数a,a^1 = a。
这个规律告诉我们,任何非零实数的1次幂都等于它本身。
例如,2^1 = 2,3^1 = 3,10^1 = 10等等。
规律3:对于任意非零实数a,a^(-n) = (1/a)^n。

同底数幂的乘法运算法则
同底数幂的乘法运算法则是一种有效的数学运算方法,它可以帮助我们快速计算出复杂的数学表达式。
它的基本原理是:如果两个数字的底数相同,那么它们的乘积等于这两个数字的幂相乘。
例如,如果我们要计算2^3 * 2^4,我们可以使用同底数幂的乘法运算法则,将它们转换为2^(3+4),即2^7,这样就可以得到结果128。
另一个例子是,如果我们要计算3^2 * 3^3,我们可以使用同底数幂的乘法运算法则,将它们转换为3^(2+3),即3^5,这样就可以得到结果243。
同底数幂的乘法运算法则不仅可以用于计算两个数字的乘积,还可以用于计算多个数字的乘积。
例如,如果我们要计算2^2 * 3^3 * 5^4,我们可以使用同底数幂的乘法运算法则,将它们转换为2^2 * 3^3 * 5^4,即2^(2+3+4) * 3^(2+3+4) * 5^(2+3+4),这样就可以得到结果2^9 * 3^9 * 5^9,即1953125。
同底数幂的乘法运算法则可以帮助我们快速计算出复杂的数学表达式,而不需要花费大量的时间和精力。
它的使用可以大大提高我们的效率,节省我们的时间和精力,使我们能够更好地利用时间来完成更多的任务。
此外,同底数幂的乘法运算法则还可以帮助我们更好地理解数学原理,更好地掌握数学知识,从而更好地应用数学知识。
总之,同底数幂的乘法运算法则是一种有效的数学运算方法,它可以帮助我们快速计算出复杂的数学表达式,提高我们的效率,节省我们的时间和精力,帮助我们更好地理解数学原理,更好地掌握数学知识,从而更好地应用数学知识。

同底数幂的乘除法a m ×a n =a m+n (n m ,都是正整数)同底数幂相乘,底数不变,指数相加。
注意底数可以是多项式或单项式。
如: (a+b)2×(a+b)3=(a+b)51、幂的乘方法则:mn n m a a =)((n m ,都是正整数) 幂的乘方,底数不变,指数相乘。
如:10253)3(=- 幂的乘方法则可以逆用:即m n n m mn a a a )()(== 如:23326)4()4(4==2、积的乘方法则:n n b a ab =)((n 是正整数) 积的乘方,等于各因数乘方的积。
如:(523)2z y x -=5101555253532)()()2(z y x z y x -=∙∙∙-3、同底数幂的除法法则:n m n m a a a -=÷(n m a ,,0≠都是正整数,且)n m 同底数幂相除,底数不变,指数相减。
如:3334)()()(b a ab ab ab ==÷4、零指数和负指数;10=a,即任何不等于零的数的零次方等于1。
ppaa1=-(p a ,0≠是正整数),即一个不等于零的数的p -次方等于这个数的p 次方的倒数。
如:81)21(233==-同底数幂的乘除法专项练习1一、填空题1、=⋅53x x ;=⋅⋅32a a a ;=⋅2x x n ;=⋅53x x =⋅4x ⋅x = ;2、=⋅-32)(x x ;=-⋅-32)()(a a ;3、=⋅10104 ;=⨯⨯32333 ;4、⋅2x =6x ;⋅-)(2y =5y ;5、=⋅++312n n x x ;=-⋅-43)()(a b a b ;6、=-⋅--n n y x y x 212)()( 二、计算;1、34a a a ⋅⋅2、()()()53222---3、231010100⨯⨯4、()()()352a a a -⋅-⋅--5、254242423a a a a a a a ⋅-⋅⋅+⋅6、()()m m 2224⨯⨯三、选择题1、333+m x 可以写成( )A 、13=m xB 、33x x m +C 、13+⨯m x xD 、33x x m ⨯ 2、3,2==nm aa ,则m n a+=( )A 、5B 、6C 、8D 、9 四、已知n 为正整数,试计算 ()()()a a a n n -⨯-⨯-++2312同底数幂的乘除法专项练习21.计算:(1)32a a ⋅=___________; (2)43)(x =___________;(3)32)(ab =___________; (4)35a a ÷=___________; (5)ba ab32552⋅-=___________; (6))2)(2(y x y x +-=___________;2.(1)当时,则的取值范围是_________。
若干个同底数幂相乘的法则同底数幂相乘的法则是数学中基本的指数运算法则之一、当我们要计算同一个底数的多个幂的乘积时,可以利用同底数幂相乘的法则进行简化运算。
下面将介绍几个常用的同底数幂相乘的法则。
1.幂的乘法法则:当求两个数的乘积的幂时,可以将底数相乘,并将指数相加。
即,对于任意的实数a,b以及整数m,n,有:a^m*a^n=a^(m+n)。
例如:2^3*2^4=(2*2*2)*(2*2*2*2)=2^(3+4)=2^7=128这个法则可以推广到任意多个同底数幂相乘的情况,即:a^m*a^n*a^p=a^(m+n+p)。
2.幂的乘方法则:当求一个幂的指数次幂时,可以将指数相乘。
即,对于任意的实数a以及整数m,n,有:(a^m)^n=a^(m*n)。
例如:(2^3)^2=(2*2*2)^2=2^(3*2)=2^6=643.幂的积法则:当求多个幂的积的幂时,可以将幂内的幂分别进行求幂操作,并将结果相乘。
即,对于任意的实数a以及整数m,n,有:(a^m)*(a^n)=a^(m+n)。
例如:(2^3)*(2^4)=(2*2*2)*(2*2*2*2)=2^(3+4)=2^7=1284.幂的除法法则:当求两个数的商的幂时,可以将底数相除,并将指数相减。
即,对于任意的实数a,b以及整数m,n,有:(a^m)/(a^n)=a^(m-n)。
例如:(2^4)/(2^3)=(2*2*2*2)/(2*2*2)=2^(4-3)=2^1=2需要注意的是,在使用这些法则时,底数必须相同。
如果底数不同,则不能直接使用同底数幂相乘的法则进行简化运算。
同底数幂相乘的法则在数学中的应用非常广泛,特别是在代数方程的计算和证明过程中。
它可以帮助我们简化复杂的指数运算,便于计算和推导。
总结起来,同底数幂相乘的法则包括幂的乘法法则、幂的乘方法则、幂的积法则和幂的除法法则。
这些法则能够帮助我们在计算同底数幂的乘积时进行简化运算,提高计算的效率。
《同底数幂的乘法》的教案第一章:同底数幂的乘法概念引入教学目标:1. 理解同底数幂的乘法概念。
2. 掌握同底数幂的乘法法则。
教学内容:1. 引入同底数幂的概念,解释同底数幂的乘法。
2. 通过举例说明同底数幂的乘法法则。
教学活动:1. 引导学生思考同底数幂的乘法问题,引发学生对同底数幂的乘法概念的兴趣。
2. 利用数学软件或教具展示同底数幂的乘法过程,帮助学生直观理解。
作业与练习:1. 让学生完成一些同底数幂的乘法练习题,巩固所学知识。
第二章:同底数幂的乘法法则教学目标:1. 掌握同底数幂的乘法法则。
2. 能够运用同底数幂的乘法法则进行计算。
教学内容:1. 讲解同底数幂的乘法法则。
2. 通过示例和练习让学生掌握同底数幂的乘法法则。
教学活动:1. 通过讲解和示例,让学生理解同底数幂的乘法法则。
2. 组织学生进行小组讨论和练习,让学生互相交流和学习。
作业与练习:1. 让学生完成一些同底数幂的乘法法则应用题,巩固所学知识。
第三章:同底数幂的乘法运算教学目标:1. 能够正确进行同底数幂的乘法运算。
2. 掌握同底数幂的乘法运算技巧。
教学内容:1. 讲解同底数幂的乘法运算规则。
2. 通过示例和练习让学生掌握同底数幂的乘法运算技巧。
教学活动:1. 通过讲解和示例,让学生理解同底数幂的乘法运算规则。
2. 组织学生进行小组讨论和练习,让学生互相交流和学习。
作业与练习:1. 让学生完成一些同底数幂的乘法运算题目,巩固所学知识。
第四章:同底数幂的乘法应用教学目标:1. 能够运用同底数幂的乘法解决实际问题。
2. 掌握同底数幂的乘法在数学中的应用。
教学内容:1. 通过实际问题引入同底数幂的乘法应用。
2. 讲解同底数幂的乘法在数学中的应用。
教学活动:1. 通过实际问题的引入,让学生理解同底数幂的乘法应用。
2. 组织学生进行小组讨论和练习,让学生互相交流和学习。
作业与练习:1. 让学生完成一些同底数幂的乘法应用题,巩固所学知识。
同底数幂的乘法概念稿子一:嘿,亲爱的小伙伴们!今天咱们来聊聊同底数幂的乘法这个有趣的数学概念。
你看啊,同底数幂,啥意思呢?其实就是底数相同的幂啦。
比如说 2 的 3 次幂乘以 2 的 4 次幂,这里面 2 就是那个相同的底数。
那同底数幂相乘有啥规律呢?这可简单啦!就把指数相加就行。
像刚才说的 2 的 3 次幂乘以 2 的 4 次幂,就等于 2 的(3 + 4)次幂,也就是 2 的 7 次幂。
为啥是这样呢?咱们来想想哈。
2 的 3 次幂就是2×2×2,2 的4 次幂是2×2×2×2,那它们相乘不就是 7 个 2 相乘嘛,所以就是2 的 7 次幂啦。
再举个例子,5 的 2 次幂乘以 5 的 3 次幂,那就是 5 的 5 次幂。
是不是还挺好玩的?学会了这个,做题可就容易多啦。
比如说让你算 3 的 4 次幂乘以 3 的 5 次幂,你一下子就能知道答案是 3 的 9 次幂。
怎么样,同底数幂的乘法是不是没那么难呀?多练练,你会更厉害的!稿子二:嗨呀,朋友们!今天咱们一起来琢磨琢磨同底数幂的乘法概念。
先来说说啥叫同底数幂。
就好比一群小伙伴,都有一个共同的“老大”,这个“老大”就是底数。
比如 10 的 2 次幂和 10 的 3 次幂,10 就是它们共同的“老大”。
那同底数幂相乘咋算呢?哈哈,超简单,只要把它们的指数加起来就行。
比如说 4 的 2 次幂乘以 4 的 3 次幂,那就是 4 的(2 + 3)次幂,也就是 4 的 5 次幂。
咱们想想为啥是这样哈。
4 的 2 次幂是两个 4 相乘,4 的 3 次幂是三个 4 相乘,那它们乘到一起,不就是五个 4 相乘嘛,所以就是 4 的 5 次幂啦。
再比如说 7 的 3 次幂乘以 7 的 4 次幂,那肯定就是 7 的 7 次幂咯。
掌握了这个小窍门,做题的时候就像有了一把神奇的钥匙,能轻松打开好多难题的大门。
不信你试试,碰到那种让你算同底数幂相乘的题目,心里是不是特有底啦?好啦,同底数幂的乘法概念咱们就聊到这儿,多练习练习,数学的世界会更精彩哟!。
同底数幂的乘除法a m ×a n =a m+n (n m ,都是正整数)同底数幂相乘,底数不变,指数相加。
注意底数可以是多项式或单项式。
如: (a+b)2×(a+b)3=(a+b)51、幂的乘方法则:mn n m a a =)((n m ,都是正整数) 幂的乘方,底数不变,指数相乘。
如:10253)3(=- 幂的乘方法则可以逆用:即m n n m mn a a a )()(== 如:23326)4()4(4==2、积的乘方法则:n n b a ab =)((n 是正整数) 积的乘方,等于各因数乘方的积。
如:(523)2z y x -=5101555253532)()()2(z y x z y x -=∙∙∙-3、同底数幂的除法法则:n m n m a a a -=÷(n m a ,,0≠都是正整数,且)n m 同底数幂相除,底数不变,指数相减。
如:3334)()()(b a ab ab ab ==÷4、零指数和负指数;10=a,即任何不等于零的数的零次方等于1。
ppaa1=-(p a ,0≠是正整数),即一个不等于零的数的p -次方等于这个数的p 次方的倒数。
如:81)21(233==-同底数幂的乘才除法专项练习1一、填空题1、=⋅53x x ;=⋅⋅32a a a ;=⋅2x x n ;=⋅53x x =⋅4x ⋅x = ;2、=⋅-32)(x x ;=-⋅-32)()(a a ;3、=⋅10104 ;=⨯⨯32333 ;4、⋅2x =6x ;⋅-)(2y =5y ;5、=⋅++312n n x x ;=-⋅-43)()(a b a b ;6、=-⋅--n n y x y x 212)()( 二、计算;1、34a a a ⋅⋅2、()()()53222---3、231010100⨯⨯4、()()()352a a a -⋅-⋅--5、254242423a a a a a a a ⋅-⋅⋅+⋅6、()()m m 2224⨯⨯三、选择题1、333+m x 可以写成( )A 、13=m xB 、33x x m +C 、13+⨯m x xD 、33x x m ⨯ 2、3,2==nm aa ,则m n a+=( )A 、5B 、6C 、8D 、9 四、已知n 为正整数,试计算 ()()()a a a n n -⨯-⨯-++2312同底数幂的乘除法专项练习21.计算:(1)32a a ⋅=___________; (2)43)(x =___________;(3)32)(ab =___________; (4)35a a ÷=___________; (5)ba ab32552⋅-=___________; (6))2)(2(y x y x +-=___________;2.(1)当时,则的取值范围是_________。
同底数幂的乘法法则同底数幂的乘法法则是指当两个数的底数相同,指数分别为a和b时,它们的乘积等于底数不变,指数相加的结果。
这个法则在数学中有着广泛的应用,特别是在代数、几何和物理等领域。
在本文中,我们将深入探讨同底数幂的乘法法则,并举例说明其应用。
首先,让我们来看一个简单的例子,2的3次方乘以2的4次方。
根据同底数幂的乘法法则,这个乘积等于2的3次方加4次方,即2的7次方。
这个例子直观地展示了同底数幂的乘法法则的运用。
接下来,让我们来证明同底数幂的乘法法则。
假设有两个数x和y,它们的底数相同,分别为a,指数分别为m和n。
根据指数的定义,x等于a的m次方,y等于a的n次方。
那么,x乘以y等于a的m次方乘以a的n次方。
根据指数的乘法法则,这个乘积等于a的m加n次方。
因此,我们得出了同底数幂的乘法法则,当底数相同时,指数相加。
同底数幂的乘法法则在代数中有着重要的应用。
例如,当我们需要计算两个多项式的乘积时,可以利用同底数幂的乘法法则来简化计算。
假设有两个多项式f(x)和g(x),它们的形式分别为:f(x) = a0x^m + a1x^(m-1) + ... + am。
g(x) = b0x^n + b1x^(n-1) + ... + bn。
其中,ai和bi分别为多项式f(x)和g(x)的系数,m和n分别为它们的最高次幂。
那么,f(x)乘以g(x)的结果可以表示为:f(x) g(x) = (a0 b0)x^(m+n) + (a0 b1 + a1 b0)x^(m+n-1) + ... + am bn。
在这个计算过程中,我们可以利用同底数幂的乘法法则来简化计算。
通过将同类项合并,我们可以得到f(x)和g(x)的乘积的最简形式,从而方便后续的计算和分析。
同底数幂的乘法法则也在几何中有着重要的应用。
例如,在计算三角函数的乘积时,我们也可以利用同底数幂的乘法法则来简化计算。
假设有两个三角函数sin(x)和cos(x),它们的乘积可以表示为sin(x) cos(x)。
6.2(1)同底数幂的乘法------学案2018.3.21
学习目标:
1. 理解同底数幂的乘法法则的由来,会用语言叙述和用字母表示幂的运算性质;掌握同底数幂相乘的乘法法则;并运用同底数幂的乘法法则进行计算;
2. 在性质推导过程中初步体验研究数学问题的一般方法,及认识事物的过程从具体到抽象,由特殊到一般再到特殊。
3. 通过自主学习,体验观察、归纳、猜想、推理证明的思维过程的快乐。
4. 要养成规范运算书写,做到步步有据,正确熟练,养成良好的学习习惯,提高运算能力。
一、 有意义的回忆:
1、什么叫乘方?_______________________________________
2、 a n 叫做____________; a 叫做___________,; n 叫做___________. a n 表示有_________个a 相_________.即可以写成a n =___________________
3.说出下列各式的底数、指数及表示的含义?
①3² ②(-3)² ③ -3² ④x ⑤(a+b)² 底数是______; 底数是______; 底数是______; 底数是_____; 底数是______; 指数是______;指数是______; 指数是______; 指数是______; 指数是______; 意义________; 意义________; 意义________; 意义________; 意义________;
二、挑战问题:试一试,会算吗?会的话,说出每一步依据;如果不会的话,说说你遇到了什么障碍?还需解决什么问题?
计算:(1) 5552x x + (2) 5352x x ∙ (3)()z xy y x 25223-∙
(4))35(222b a ab ab + (5) (-3a 2)3 • (-2a)4 (6)(x-1)(x 2+x+1)
三、新知探究:你认真思考相信一定可以完成的!
1、有一种国产新型电子计算机,每秒钟可以作108次运算,103秒可以作多少次运算呢?
解:______________________________________________
答:________________________________________________
2、试试看: 102 ×103103 ×105=________________;108 ×103
3、再试试:计算
a 2·a 3=__________; a 3·a 5a 5·a 6=______; a 3·a 84、并猜想a m ·a n =?(m,n
用文字语言叙述你的结论:
5、此公式应注意问题 :
(1)底数a 可以表示____________________________;
(2)m ,n 都是__________数;
(3)适用条件: ① ②
结论:
6.巩固练习: 1.
判断下列各式是否正确?说明理由,并改正:
①a 5·
a 5=2 a 10( )
②1055a a a =+( ) ③933b b b =⋅( ) ④6332b b b =+( ) ⑤65a a a =⋅( ) ⑥65a a a =+( ) ⑦33332x x x =+( )⑧62424)(x x x x x =⋅=-⋅-( )
2.光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?
7、新知拓展:
(1)当三个或三个以上的同底数幂相乘时,是否也符合上述性质?请你把三个同底数幂相乘的性质用公式表示出来:
推广:
(2)运算性质反之是否成立?如何表示? 逆向应用:
四、应用:试试自己的能力,注意步骤要规范、严谨
例1. 计算:
A 组:①35·36 ;②107×103 ;③ x 3·x 12 ④ y m-1·y ;⑤ a m-1·a m+1 ;
是正整数)
,( _______________n m a n m =+思考:同底数幂乘法与整式加减的区别:
B 组:例2:计算
① a 2·a 3a 5; ② x·x 2·x 3x 5; ③ ④9×3×27×34 ⑤(a-b)2· (a-b)3
想一想: (-a)n ( n 为正整数)表示的意义是什么? 如何去掉(-a)n 的括号?
C 组:例3:计算 ① ; ② ③ -x 2·x 6 ; ④ (-m)3·(-m)2 ;
⑤(b-a)4· (a-b)3 ⑥ ; ⑦(-m)m-1·
(-m)m+2;
⑧ ⑨x 3·x 4 + 3x 2·x·x 4+ (-x)·(-x)3·x 3
拓展提高:
()()()()()()写出三组)
?(?a 则,18a 已知)7(__________则,42;1282已知6__________
a 则,3,2a 已知5_______2则,32已知4________
则;9273若3;
2_______;
x ,则82若1n
m m m 3x x x 7(___)2x ============⨯==⋅⋅==++++n m n m n n n a m a x x x x x
五:学习小结:把你这节课学习的收获记录下来,和同伴交流你的收获吧! 知识方面:
能力方面:
数学思想方面:
研究数学问题的方法:
还有哪些学习困惑:
()()()x y x y y x ---23()62a a ⋅-62a
a ⋅-234x x x x ⋅+
⋅。