【免费下载】平行四边形真的不是轴对称图形吗？

轴对称图形的定义及常见图形
轴对称图形的含义
在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，并且对称轴用点画线表示。

这时，我们也说这个图形关于这条直线对称。

常见的轴对称图形
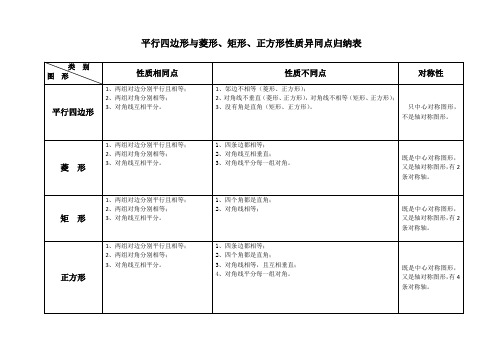
1.等腰三角形有一条对称轴，是顶角平分线所在的直线。

2.等边三角形有三条对称轴，分别是三个顶角平分线所在的直线。

3.矩形有两条对称轴，是相邻两边的垂直平分线。

4.正方形有四条对称轴，是相邻两边的垂直平分线和对角线所在的直线。

5.菱形有两条对称轴，是对角线所在的直线。

轴对称和轴对称图形区别
1.轴对称是指两个图形间的位置关系，轴对称图形是指一个具有特殊形状的图形。

2.轴对称涉及两个图形，轴对称图形是对一个图形而言的。

3.如果把轴对称图形沿对称轴分成两部分（即看成两个图形），那么这两个图形就关于这条直线成轴对称。

如果把轴对称的两个图形看成一个整体，那么它就是一个轴对称图形。

2024-2025学年浙江省嘉兴市小学四年级数学上册期中质量考试试卷班级：________________ 学号：________________ 姓名：______________一、单选题（每题3分）1.下列各数中，最接近2的数是（）。

A. 1.9B. 1.99C. 2.01D. 2.1答案：B解析：本题主要考察学生对小数大小比较的理解。

题目要求找出最接近2的数，通过比较各选项与2的差值，可以得出1.99与2的差值最小，因此选B。

2.一个平行四边形，若高增加5厘米，底不变，面积就增加45平方厘米；若高不变，底减少5厘米，面积就减少30平方厘米。

原来平行四边形的面积是（）平方厘米。

A. 54B. 45C. 90D. 108答案：A解析：本题考查平行四边形的面积公式。

设平行四边形的高为h厘米，底为b厘米。

根据题目条件，我们可以列出两个方程：5b = 45 和h×5 = 30。

解这两个方程得到b = 9，h = 6。

最后，原平行四边形的面积= b×h = 9×6 = 54（平方厘米）。

3.一个长方体的长、宽、高都扩大到原来的2倍，它的体积扩大到原来的（）倍。

A. 2B. 4C. 6D. 8答案：D解析：本题考查长方体体积的计算。

设长方体的长、宽、高分别为a、b、c，原体积为V1 = a×b×c。

当长、宽、高都扩大到原来的2倍时，新的长、宽、高分别为2a、2b、2c，新体积V2 = 2a×2b×2c = 8abc = 8V1。

因此，体积扩大到原来的8倍，选D。

4.在一个除法算式中，除数是6，商是12，被除数最大是（）。

A. 72B. 71C. 70D. 69答案：B解析：本题考查除法运算中余数的概念。

在除法中，余数必须小于除数。

已知除数是6，商是12，那么被除数 = 除数×商 + 余数。

要使被除数最大，余数必须取最大值5（因为余数必须小于6）。

平行四边形的性质平行四边形是一种特殊的四边形，具有独特的性质和特点。

本文将逐一介绍平行四边形的几个重要性质，让我们深入了解这一几何形态。

1. 相对边平行性质平行四边形的最基本性质就是它的对边是平行的。

这意味着平行四边形的任意两条对边都是平行的。

例如，若ABCD为平行四边形，那么AB和CD、AD和BC也一定是平行的。

这一性质是平行四边形最为明显和重要的特征之一。

2. 相对边长度性质当我们研究平行四边形的性质时，不仅仅是对边的平行性是关键，对边的长度也有一定的关系。

对边长度性质指的是平行四边形的相对边长相等。

具体而言，平行四边形的相对边长相等，即AB = CD，AD = BC。

这一性质进一步强调了平行四边形的对称性与整体结构。

3. 对角线性质平行四边形的对角线有一些独特的性质。

首先，平行四边形的对角线相互平分。

也就是说，如果ABCD是平行四边形，那么对角线AC和BD将把平行四边形分成两个面积相等的三角形。

其次，平行四边形的对角线交点称为对角线的交点，通常用字母O表示。

对角线交点O将对角线AC和BD平分，并且连线AO与BO以及CO与DO的长度相等。

最后，对角线AC和BD的长度满足关系：AC² + BD² = 2(AB² + AD²)。

这一关系进一步表明了平行四边形的几何关系。

4. 内角性质平行四边形的内角性质非常特殊。

它的重要特点是相邻内角的和为180度，即相邻内角对是补角。

例如，若ABCD是平行四边形，那么∠A + ∠D = 180度，∠B + ∠C = 180度。

此外，平行四边形的对角线相交处的四个内角也是相等的。

这一性质使得我们能够更加深入地研究平行四边形的内部结构和角度特点。

5. 垂直性质平行四边形还具有一项重要的垂直性质。

当平行四边形的一个内角与一个外角相等时，这两个角组成对顶角，即对顶角是相等的。

例如，若∠A和∠C分别是平行四边形ABCD的内角和外角，且∠A = ∠C，那么∠B和∠D也一定相等。

平行四边形真的不是轴对称图形吗？杨建维2010年6月29日前段时间，在某处听到小学数学四年级的《轴对称图形》一节课，教师在课中设计了这样一个问题：学过的平面图形中哪些是轴对称图形，哪些不是轴对称图形？学生在交流到平行四边形是否是轴对称图形时，教师给学生非常肯定的结论：平行四边形不是轴对称图形。

听到这个结论引发了我的思考：平行四边形真的不是轴对称图形吗？说到平行四边形到底是不是轴对称图形，有两个问题不能回避，那就是什么是轴对称图形和什么是平行四边形？青岛版小学数学教科书第八册中《图案美》单元对轴对称图形有比较明确的概念：将图形沿着一条直线对折，如果直线两侧的部分能够完全重合，这样的图形叫做轴对称图形，折痕所在的这条直线叫做它的对称轴。

在《小学数学研究》的第九章《小学数学中的几何变换》中对轴对称图形的概念进行了更为数学化的描述：两个图形具有一一变换的关系，如果以每对对应点为端点的线段都和同一条直线垂直且被平分，那么称这种变换为轴对称（或直线反射），每对对应点互称对称点，垂直平分对称点所连线段的直线叫做对称轴。

事实上，轴对称刻画的是两个图形之间的一种关系，也就是说，如果两个图形中的一个图形通过反射变换，变成了另一个图形，那么，这两个图形就是以反射轴为对称轴的轴对称图形。

也就是说，对于某两个图形，如果沿某条直线对折，两个图形在直线两旁的部分能完全重合，那么，这样的两个图形通常叫成轴对称的（两个图形），简称成轴对称。

特别地，如果一个图形的一部分通过反射变换成了这个图形的另一部分，那么，这个图形就是一个轴对称图形。

青岛版小学数学教科书第八册在《水产养殖场》中对平行四边形也有定义，就是两组对边分别平行的四边形叫做平行四边形。

《新课标小学数学教学素材与方略》在《空间与几何》部分对平行四边形的特征有以下归纳：平行四边形的两组对边分别平行且相等；平行四边形具有易变形、不稳定的特性；平行四边形的四个内角和是360。

，且两组内对角大小分别相等；平行四边形对角线互相平分。

平面几何平行四边形的性质平行四边形是平面几何中一种重要的图形，具有独特的性质和特征。

本文将介绍平行四边形的定义、性质以及相关定理，探讨其在几何学中的应用。

一、平行四边形的定义平行四边形是指四边形的对边两两平行的四边形。

简单来说，对于一个四边形，如果它的对边互相平行，则称之为平行四边形。

除了对边平行外，平行四边形还具有其他重要的性质。

二、平行四边形的性质1. 对边性质：平行四边形的对边长度相等。

这意味着平行四边形的相对边长是相等的，可以用于解题和判断。

2. 对角线性质：平行四边形的对角线互相平分。

具体而言，平行四边形的对角线AB和CD交于E点，那么AE和EC的长度相等，BE和ED的长度也相等。

3. 对角线垂直性质：平行四边形的对角线互相垂直。

即平行四边形的对角线交于一点时，也是互相垂直的。

4. 同位角性质：平行四边形的同位角相等。

同位角是指位于平行四边形相邻顶点之间的内角，这些角的度数是相等的。

5. 内角和性质：平行四边形的内角和为360度。

我们可以通过这个性质来验证一个四边形是否为平行四边形。

三、平行四边形的相关定理除了上述的基本性质外，还有一些与平行四边形相关的定理。

1. 平行四边形的定理：如果一个四边形的对边互相平行，则它是一个平行四边形。

2. 平行四边形的推论定理：如果一个四边形的对边长度相等，则它是一个平行四边形。

3. 平行四边形的性质定理：如果一个四边形的对角线互相垂直，则它是一个平行四边形。

以上定理可以帮助我们在解题过程中判断和证明一个四边形是否为平行四边形，并且使用这些定理可以简化证明过程，提高解题效率。

四、平行四边形的应用平行四边形在几何学中有广泛的应用。

下面列举几个常见的应用场景：1. 计算面积：平行四边形的面积计算公式为面积 = 底边长 ×高度。

通过求解平行四边形的面积，我们可以对平行四边形进行比较和分类。

2. 证明性质：平行四边形的性质可以在证明过程中起到重要的作用。

平行四边形的定义,性质及判定方法平行四边形的定义、性质及判定方法在我们的数学世界中，平行四边形是一种非常常见且重要的几何图形。

它不仅在数学理论中有着重要地位，还在实际生活中有着广泛的应用。

接下来，就让我们一起深入了解平行四边形的定义、性质以及判定方法。

一、平行四边形的定义平行四边形是指在同一平面内，两组对边分别平行的四边形。

这是平行四边形最基本的特征，也是判断一个四边形是否为平行四边形的首要条件。

比如说，我们可以想象一个由四根木条组成的框架，如果相对的两根木条始终保持平行，那么这个框架所围成的四边形就是平行四边形。

二、平行四边形的性质1、对边平行且相等平行四边形的两组对边分别平行，这是定义所决定的。

同时，这两组对边的长度也是相等的。

例如，在平行四边形 ABCD 中，AB 平行且等于 CD，AD 平行且等于 BC。

2、对角相等平行四边形的两组对角分别相等。

也就是说，∠A ＝∠C，∠B ＝∠D。

3、邻角互补相邻的两个角之和为 180 度。

比如∠A 和∠B 是邻角，那么∠A ＋∠B ＝ 180°；同样，∠B 和∠C，∠C 和∠D，∠D 和∠A 也是如此。

4、对角线互相平分平行四边形的两条对角线相交于一点，并且这一点将每条对角线都平分成两段。

例如，在平行四边形 ABCD 中，对角线 AC 和 BD 相交于点 O，那么 AO ＝ CO，BO ＝ DO。

5、平行四边形是中心对称图形对称中心是两条对角线的交点。

将平行四边形绕着对角线的交点旋转 180 度后，能够与原来的图形重合。

这些性质在解决与平行四边形相关的问题时非常有用，我们可以通过已知条件灵活运用这些性质来得出所需的结论。

三、平行四边形的判定方法1、两组对边分别平行的四边形是平行四边形这是根据平行四边形的定义直接得出的判定方法。

如果一个四边形的两组对边都相互平行，那么它一定是平行四边形。

2、两组对边分别相等的四边形是平行四边形例如，在四边形 ABCD 中，如果 AB ＝ CD，AD ＝ BC，那么四边形 ABCD 就是平行四边形。

平行四边形是轴对称图形吗?作者：梁万美来源：《云南教育·小学教师》2011年第03期在一次全县小学五年级数学课堂教学竞赛中，有幸观摩了人教版五年级下册“轴对称”一课的教学实况。

其中的精彩片段，至今记忆犹新。

新课部分，教师按课前的预设上得井然有序。

在做练习时，老师让学生判断学过的平面图形中哪些是轴对称图形，哪些不是轴对称图形。

当判断平行四边形是不是轴对称图形时，出现了两种答案，于是一场精彩的辩论开始了。

正是课堂生成的这场争论，使这节课呈现出异样的精彩。

现撷取精彩片段以飨同人。

师：请同学们仔细观察下面的图形，判断哪些是轴对称图形，哪些不是轴对称图形？（教师逐一出示长方形、正方形、圆形、平行四边形等。

当学生判断到一般的平行四边形时，出现了分歧，“是”与“不是”尖锐对立着。

）师：认为一般的平行四边形是轴对称图形的同学请举手。

（大部分学生举手。

）师：你们有什么办法证明自己的观点是正确的呢？生：动手折一折就可以验证。

（好多学生动手折平行四边形。

）师：通过动手折，大家对平行四边形是不是轴对称图形已有自己的看法，下面就请发表意见吧！生1：我认为平行四边形肯定不是轴对称图形，你们看（边说边演示），我把平行四边形横着折、竖着折、斜着折，不管怎么折，两侧的图形都不能重合，所以我认为平行四边形不是轴对称图形。

生2：我认为平行四边形是轴对称图形，因为沿着它的高剪开，可以拼成一个长方形，长方形是轴对称图形，所以平行四边形也是轴对称图形。

生3：你说得不对，判断一个图形是不是轴对称图形，要沿着一条直线对折，再看“折痕”两边的图形是不是完全重合。

生4：用剪刀剪后拼成的长方形不是我们要判断的原来的平行四边形。

生5：我是对折，也不用剪刀剪。

你们看我把平行四边形对折以后再对折，两侧的图形就能完全重合，所以我认为平行四边形是轴对称图形。

师：你们觉得有道理吗？生6：我认为折两次是错误的。

轴对称图形是沿着一条直线对折，直线两边的图形要能够完全重合在一起。

高中数学几何图形中的对称分析对称是数学图形中的一种重要性质，它在几何、代数、分析等多个领域有着广泛的应用。

在高中数学中，对称也是学生们必须掌握的一个重要知识点。

本文将通过分析高中数学中的一些几何图形，探讨对称的性质和应用。

一、轴对称图形轴对称图形是指沿着一条直线对折，如果左右两边能够完全重合，那么这个图形就是轴对称图形。

常见的轴对称图形有正方形、等腰三角形、圆形等。

轴对称图形的对称轴可以是直线，也可以是曲线。

例如，圆的对称轴就是圆所在的整个平面。

在轴对称图形中，对称轴两侧的图形具有相似的性质。

例如，在等腰三角形中，对称轴两侧的边长相等、角度相等，性质相似。

因此，可以通过分析一个轴对称图形的对称轴，来判断另一个图形的性质。

二、中心对称图形中心对称图形是指将图形绕着某一点旋转180度后，能够与原来的图形重合。

常见的中心对称图形有矩形、菱形、平行四边形等。

中心对称图形的对称中心可以是任意一点，也可以是两条直线。

例如，矩形的对称中心就是对角线的交点，菱形的对称中心是两条对角线的交点。

在中心对称图形中，可以通过分析一个图形的对称中心或对称轴，来判断另一个图形的性质。

例如，矩形具有稳定性、平行四边形具有传递性等性质，这些性质都可以通过中心对称或轴对称的性质来解释。

三、对称在几何中的应用对称在几何中的应用非常广泛，它可以用来解决一些与角度、边长、面积等问题相关的问题。

例如，在求圆的面积时，可以通过轴对称将圆分成两个完全相等的扇形，再乘以π来计算；在求矩形周长时，可以通过中心对称将矩形分成两个完全相等的部分，再乘以两倍的边长来计算周长。

此外，对称还可以用来解决一些与角度问题相关的问题。

例如，在求一个角度的补角或余角时，可以通过轴对称将角度旋转180度来得到补角或余角；在判断两个角是否相等时，可以通过中心对称将两个角分别旋转180度后是否重合来判断；在证明三角形内角和为180度时，可以通过将三角形分成两个完全相等的扇形来证明。

平行四边形的知识点
平行四边形的知识点：平行四边形（Parallelogram），是在同一个二维平面内，由两组平行线段组成的闭合图形。

平行四边形一般用图形名称加四个顶点依次命名。

注：在用字母表示四边形时，一定要按顺时针或逆时针方向注明各顶点。

在欧几里德几何中，平行四边形是具有两对平行边的简单（非自相交）四边形。

平行四边形的相对或相对的侧面具有相同的长度，并且平行四边形的相反的角度是相等的。

1、平行四边形是中心对称图形，对称中心是两对角线的交点;
2、过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形;
3、如果一个四边形是平行四边形，那么这个四边形的邻角互补;
4、如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等;
5、如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等;
6、如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分;
7、平行四边形对角线把平行四边形面积分成四等份;
8、平行四边形中，两条在不同对边上的高所组成的夹角，较小的角等于平行四边形中较小的角，较大的角等于平行四边形中较大的角。