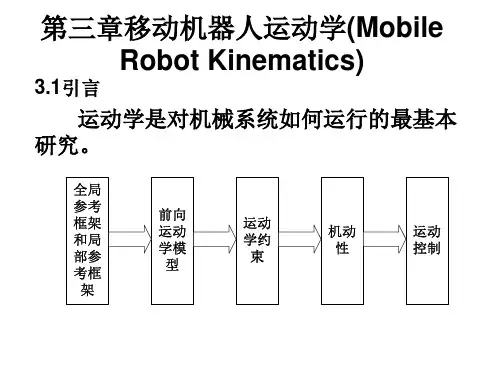
机器人学第3章 机器人运动学
- 格式:ppt
- 大小:1.22 MB
- 文档页数:34


第三章机器人运动学机器人运动学是研究机器人如何在二维或三维空间中进行运动的学科。
它涉及到机器人的轨迹规划、运动控制和路径规划等重要内容。
本章将介绍机器人运动学的基本概念和常用模型,帮助读者全面了解机器人的运动规律和控制原理。
1. 机器人运动学的基本概念机器人运动学是研究机器人位置和姿态变化的学科,包括正运动学和逆运动学两个方面。
正运动学研究机器人的末端执行器的位置和姿态如何由关节变量确定;逆运动学则研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值。
机器人的运动学建模一般采用DH(Denavit-Hartenberg)参数表示方法。
DH 参数是由Denavit和Hartenberg提出的一种机器人坐标系的选择和旋转轴的确定方法。
通过定义一系列关节坐标系,建立起机器人的坐标系链,并确定各个关节的旋转轴和约定的方向,可以方便地描述机器人的运动学特性。
2. 机器人正运动学机器人正运动学是研究机器人末端执行器位置和姿态如何由关节变量确定的问题。
在机器人的正运动学中,常用的方法有几何法和代数法。
2.1 几何法几何法是一种较为直观的方法,通过对机器人各个关节坐标系的位置和旋转进行推导,得到机器人末端执行器的位置和姿态。
几何法适用于无约束和无外力干扰的情况,可以简单快速地推导出机器人的正运动学方程。
2.2 代数法代数法是一种基于运动学链的代数运算的方法,通过DH参数建立起机器人的坐标系链,并通过矩阵运算推导出机器人的正运动学方程。
代数法在机器人正运动学的推导和计算过程中更具有普适性和灵活性。
3. 机器人逆运动学机器人逆运动学是研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值的问题。
机器人逆运动学在机器人运动规划和路径控制中起到重要的作用。
机器人逆运动学的求解一般采用迭代方法,通过迭代计算来逼近解析解,实现对机器人关节变量的求解。
逆运动学的求解过程中可能会出现奇异点和多解的情况,需要通过约束条件和优化方法来处理。



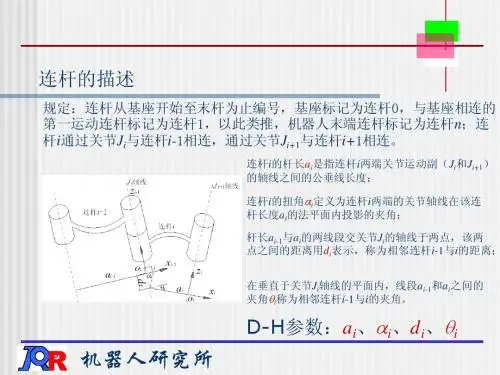



第3章工业机器人运动学和动力学机器人操作臂可看成一个开式运动链,它是由一系列连杆通过转动或移动关节串联而成。
开链的一端固定在基座上,另一端是自由的,安装着工具,用以操作物体,完成各种作业。
关节由驱动器驱动,关节的相对运动导致连杆的运动,使手爪到达所需的位姿。
在轨迹规划时,最感兴趣的是末端执行器相对于固定参考系的空间描述。
为了研究机器人各连杆之间的位移关系,可在每个连杆上固接一个坐标系,然后描述这些坐标系之间的关系。
Denavit和Hartenberg提出一种通用方法,用一个4*4的齐次变换矩阵描述相邻两连杆的空间关系,从而推导出“手爪坐标系”相对于“参考系”的等价齐次变换矩阵,建立出操作臂的运动方程。
称之为D-H矩阵法。
3.1 工业机器人的运动学教学时数:4学时教学目标:理解工业机器人的位姿描述和齐次变换;掌握齐次坐标和齐次变换矩阵的运算;理解连杆参数、连杆变换和运动学方程的求解;教学重点:掌握齐次变换及运动学方程的求解教学难点:齐次变换及运算教学方法:讲授教学步骤:齐次变换有较直观的几何意义,而且可描述各杆件之间的关系,所以常用于解决运动学问题。
已知关节运动学参数,求出末端执行器运动学参数是工业机器人正向运动学问题的求解;反之,是工业机器人逆向运动学问题的求解。
3.1.1 工业机器人位姿描述1.点的位置描述在选定的指教坐标系{A}中,空间任一点P的位置可用3*1的位置矢量表示,其左上标代表选定的参考坐标系。
2.点的齐次坐标如果用四个数组成4*1列阵表示三维空间直角坐标系{A}中点P,则该列阵称为三维空间点P的齐次坐标,如下:必须注意,齐次坐标的表示不是惟一的。
我们将其各元素同乘一个非零因子后,仍然代表同一点P,即其中:,,。
该列阵也表示P点,齐次坐标的表示不是惟一的。
3.坐标轴方向的描述用i、j、k分别表示直角坐标系中X、Y、Z坐标轴的单位向量,用齐次坐标来描述X、Y、Z轴的方向,则有,,从上可知,我们规定:4*1列阵中第四个元素为零,且,则表示某轴(某矢量)的方向。

教案首页课程名称农业机器人任课教师李玉柱第3章机器人运动学和动力学计划学时 3教学目的和要求:1.概述,齐次坐标与动系位姿矩阵,了解平移和旋转的齐次变换;2.机器人的运动学方程的建立与求解*;3.机器人的动力学*重点:1.机器人操作机运动学方程的建立及求解;2.工业机器人运动学方程3.机器人动力学难点:1. 机器人动力学方程及雅可比矩阵基本原理思考题:1.简述齐次坐标与动系位姿矩阵基本原理。
2.连杆参数及连杆坐标系如何建立?3.机器人动力学方程及雅可比矩阵基本原理是什么?第3章机器人运动学和动力学教学主要内容:3.2 齐次坐标与动系位姿矩阵3.3 齐次变换3.4 机器操作机运动学方程的建立与求解3.5 机器人运动学方程3.6 机器人动力学本章将主要讨论机器人运动学和动力学基本问题。
先后引入了齐次坐标与动系位姿矩阵、齐次变换,通过对机器人的位姿分析,介绍了机器人运动学方程;在此基础上有对机器人运动学方程进行了较为深入的探讨。
3.1 概述机器人,尤其是关节型机器人最有代表性。
关节型机器人实质上是由一系列关节连接而成的空间连杆开式链机构,要研究关节型机器人,必须对运动学和动力学知识有一个基本的了解。
分析机器人连杆的位置和姿态与关节角之间的关系,理论称为运动学,而研究机器人运动和受力之间的关系的理论则是动力学。
3.2 齐次坐标与动系位姿矩阵3.2.1 点的位置描述在关节型机器人的位姿控制中,首先要精确描述各连杆的位置。
为此,先定义一个固定的坐标系,其原点为机器人处于初始状态的正下方地面上的那个点,如图3-1(a)所示。
记该坐标系为世界坐标系。
在选定的直角坐标系{A}中,空间任一点P的位置可以用3×1的位置向量A P表示,其左上标表示选定的坐标系{A},此时有A P=XYZ P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦式中:P X、P Y、P Z—点P在坐标系{A}中的三个位置坐标分量,如图3-1(b)。
3.2.2 齐次坐标将一个n维空间的点用n+1维坐标表示,则该n+1维坐标即为n维坐标的齐次坐标....。