四点共圆基本判断方法超全 ppt课件
- 格式:ppt
- 大小:1.08 MB
- 文档页数:11


四点共圆知识嘿,朋友!今天咱们来聊聊神秘又有趣的“四点共圆”知识。
你知道吗,四点共圆就像是四个小伙伴手拉手围成一个圈圈,共同玩耍。
那到底啥是四点共圆呢?简单说,就是平面上的四个点在同一个圆上。
这有啥用呢?用处可大了去啦!比如在几何题里,要是能发现四点共圆,那解题思路可能就像开了闸的洪水,一下子涌出来了。
咱们先来说说怎么判断四点共圆。
有一种方法叫“对角互补法”。
啥意思呢?就是如果四边形的对角互补,那这四个点就在同一个圆上。
这就好比两个脾气互补的朋友,能相处得特别好,一起在一个圈子里快乐玩耍。
再比如说“同弦所对的圆周角相等”。
这就好像一把钥匙开一把锁,同一个弦对应的圆周角,那肯定是“一伙儿”的,这四个点也就共圆啦。
四点共圆还有很多神奇的性质呢。
比如说,共圆的四个点所连成的同侧共底的两个三角形的顶角相等。
这是不是有点像双胞胎,长得像,性格也差不多。
还有啊,如果四点共圆,那么其中一个点到另外三个点的距离之积等于另外一个点到这三个点的距离之积。
这是不是很奇妙?就好像是这四个点之间有着一种神秘的约定。
那怎么在实际解题中运用四点共圆呢?给你举个例子。
有个几何题,给了你一些角度和线段长度的条件,怎么都解不出来。
这时候你突然发现,如果能证明这四个点共圆,那就能利用四点共圆的性质找到突破口,一下子就把难题给解决了,是不是感觉超级爽?学习四点共圆知识,就像是探索一个神秘的宝藏,每发现一个新的性质或者方法,都像是找到了一颗闪闪发光的宝石。
所以啊,朋友,别小看这四点共圆的知识,它可是几何世界里的一把神奇钥匙,能帮你打开一扇又一扇难题的大门,让你的数学之旅更加精彩!你说,这么有趣又有用的知识,咱们能不好好学吗?。



四点共圆的判定与性质一、四点共圆的判定(一)判定方法1、若四个点到一个定点的距离相等,则这四个点共圆。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
5、同斜边的直角三角形的顶点共圆。
6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理)。
7、若AB、CD两线段延长后相交于P。
且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理)。
8、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆(托勒密定理的逆定理。
(二)证明1、若四个点到一个定点的距离相等,则这四个点共圆。
若可以判断出OA=OB=OC=OD,则A、B、C、D四点在以O为圆心OA为半径的圆上。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
若∠A+∠C=180°或∠B+∠D=180°,则点A、B、C、D四点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
若∠B=∠CDE,则A、B、C、D四点共圆证法同上。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
若∠A=∠D或∠ABD=∠ACD,则A、B、C、D四点共圆。
5、同斜边的直角三角形的顶点共圆。
如图2,若∠A=∠C=90°,则A 、B 、C 、D 四点共圆。
6、若AB 、CD 两线段相交于P 点,且PA ×PB=PC ×PD ,则A 、B 、C 、D 四点共圆(相交弦定理的逆定理)。
7、若AB 、CD 两线段延长后相交于P 。


第14课 四点共圆一、基本结论与方法:判断四点共圆的方法有:1.到定点等距离的几个点在同一个圆上;2.同斜边的直角三角形的各顶点共圆;3.同底同侧张角相等的三角形的各顶点共圆;4、如果一个四边形的一组对角互补,那么它的四个顶点共圆;5、如果四边形的一个外角等于它的内对角,则它的四个顶点共圆;6、四边形的对角线相交于点P ,且PA•PC=PB•PD,那么四个顶点共圆;7、四边形ABCD 的一组对边AB 、DC 的延长线交于点P ,若PA•PB=PC•PD, 那么四个顶点共圆.托勒密定理:圆内接四边形的对边之积的和,等于对角线之积。
即:如图,四边形ABCD 内接于圆,求证:BD AC BC AD CD AB ⋅=⋅+⋅.DB二、例题与习题例1、如图,ABCD 是等腰梯形,求证:BD 2=AB•CD+BC 2.CD 例2、△ABC 中,∠A:∠B:∠C=1:2:4,:求证:BC AC AB 111=+A D例3、在边长为1的正七边形中,对角线AD=a,BG=b,求证:22)()(ab b a b a =-+.C 例4、两圆相交于A 、B,P 是BA 延长线上一点,PCD 、PEF 分别是两圆的割线,求证:C 、D 、E 、F 四点共圆。
F例5、由圆外定直线上任意点,引圆的两条切线,求证:两切点的连线必经过某定点。
CA例6、点P 是正三角形外接圆的劣弧AB 上一点,连接PC 交AB 于D ,求证:(1)PA+PB=PC;(2)111PA PBPD +=.例7、P为△ABC内一点,D、E、F分别在三角形的边上,已知P、D、C、E四点共圆,P、E、A、F四点共圆,求证:B、D、P、F四点共圆。
例8、设凸四边形ABCD的对角线互相垂直,垂足为E,证明:点E关于AB、BC、CD、DA 的对称点也共圆。
A例9、两个圆彼此相交,从它们的对称中心引出两条射线交圆周于不在同一直线上的四个点,证明:这四个点共圆。
例10、梯形ABCD的两条对角线相交于点K,分别以梯形的两腰围直径作圆,点K位于两圆之外,证明:由K向两圆所作的切线长度相等。
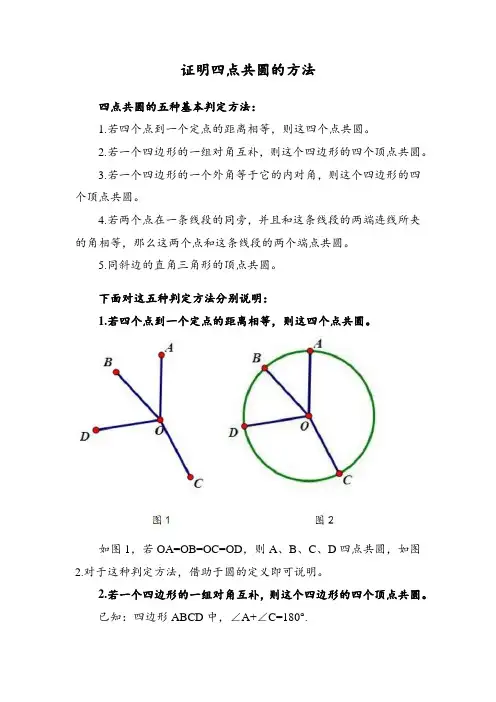
证明四点共圆的方法四点共圆的五种基本判定方法:1.若四个点到一个定点的距离相等,则这四个点共圆。
2.若一个四边形的一组对角互补,则这个四边形的四个顶点共圆。
3.若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆。
4.若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆。
5.同斜边的直角三角形的顶点共圆。
下面对这五种判定方法分别说明:1.若四个点到一个定点的距离相等,则这四个点共圆。
如图1,若OA=OB=OC=OD,则A、B、C、D四点共圆,如图2.对于这种判定方法,借助于圆的定义即可说明。
2.若一个四边形的一组对角互补,则这个四边形的四个顶点共圆。
已知:四边形ABCD中,∠A+∠C=180°.求证:四边形ABCD内接于一个圆(A,B,C,D四点共圆).证明:用反证法过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,若C在圆外,设BC交圆O于C’,连结DC’(如图3),据圆内接四边形的性质得∠A+∠DC’B=180°,∵∠A+∠C=180°∴∠DC’B=∠C 这与三角形外角定理矛盾,故C不可能在圆外.类似地可证C不可能在圆内.∴C在圆O上,也即A,B,C,D四点共圆.3.若一个四边形的外角等于它的内对角,则这个四边形的四个顶点共圆。
证明方法同2,把外角等于内对角的情况转化为一组对角互补4.若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆。
已知:如图4,BC同侧△ABC和△CBD,且∠A=∠D.求证:A、B、C、D四点共圆.证明:假设四点不在同一圆上,作△ABC外接圆,则D点不在圆上,∵∠A,∠D共用弧AB,∴∠A≠∠D,与实际不符,∴D点在△ABC外接圆上,故A、B、C、D四点共圆。
5.同斜边的直角三角形的顶点共圆.证明方法:取斜边的中点,再连接斜边中点和直角顶点,利用斜边中点等于斜边一半即可说明。

四点共圆的判定与性质一、四点共圆的判定(一)判定方法1、若四个点到一个定点的距离相等,则这四个点共圆。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
5、同斜边的直角三角形的顶点共圆。
6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理)。
7、若AB、CD两线段延长后相交于P。
且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理)。
8、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆(托勒密定理的逆定理。
(二)证明1、若四个点到一个定点的距离相等,则这四个点共圆。
若可以判断出OA=OB=OC=OD,则A、B、C、D四点在以O为圆心OA为半径的圆上。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
若∠A+∠C=180°或∠B+∠D=180°,则点A、B、C、D四点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
若∠B=∠CDE,则A、B、C、D四点共圆证法同上。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
若∠A=∠D或∠ABD=∠ACD,则A、B、C、D四点共圆。
5、同斜边的直角三角形的顶点共圆。
如图2,若∠A=∠C=90°,则A 、B 、C 、D 四点共圆。
6、若AB 、CD 两线段相交于P 点,且PA ×PB=PC ×PD ,则A 、B 、C 、D 四点共圆(相交弦定理的逆定理)。
7、若AB 、CD 两线段延长后相交于P 。

第十五讲 四点共圆“四点共圆”问题在数学竞赛中经常出现,这类问题一般有两种形式:一是以“四点共圆”作为证题的目的,二是以“四点共圆”作为解题的手段,为解决其他问题铺平道路. 一、四点共圆如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
1、四点共圆的性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等; (2)圆内接四边形的对角互补;(3)圆内接四边形的一个外角等于它的内对角。
以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。
2、四点共圆的判定方法:(1)从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆.(2)把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆。
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆。
)(3)把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等(同弧所对的圆周角相等),从而即可肯定这四点共圆.(若能证明其两顶角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。
)(4)把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆(相交弦定理的逆定理);或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.(割线定理逆定理) (5)证被证共圆的点到某一定点的距离都相等,从而确定它们共圆.既连成的四边形三边中垂线有共同交点,即可肯定这四点共圆.(6)同斜边的两个直角三角形的四个顶点共圆,其斜边为圆的直径。
二、托勒密定理及其逆定理托勒密定理是平面几何中的一个重要定理,它揭示了圆内接四边形的对角线与边的关系。
1.托勒密定理:圆内接四边形两组对边乘积之和,等于两条对角线的乘积。
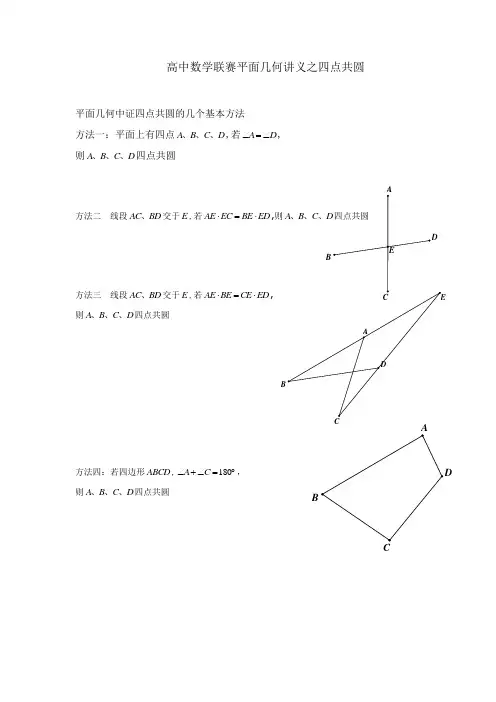
BB高中数学联赛平面几何讲义之四点共圆平面几何中证四点共圆的几个基本方法 方法一:平面上有四点A B C D 、、、,若A D ∠=∠, 则A B C D 、、、四点共圆方法二 线段AC BD 、交于E ,若AE EC BE ED ⋅=⋅,则方法三 线段AC BD 、交于E ,若AE BE CE ED ⋅=⋅, 则A B C D 、、、四点共圆方法四:若四边形ABCD ,180A C ∠+∠=︒, 则A B C D 、、、四点共圆DCBPB方法四、已知 AD 是ABC △内角或外角平分线,AB AC ≠,且BD DC =,则A B C 、、证明 设BAD α∠=,因为AD AD DB DC =,所以sin sin sin sin B C BAD CAD=∠∠,所以sin sin B C =,内角时180B C +=︒,外角时B C =,所以A B C D 、、、四点共圆托勒密定理:Tolemy(托勒密定理)若四边形ABCD 是圆O 内接四边形,则AD •BC+AB •CD=AC •BD证明 在AC 上取点E,使∠EDC=∠ADB,因为∠ABD=∠ACD,所以△ABD ∼△EDC,△ADE ∼△BDC ,于是(AB/CE)=(DB/DC),(AD/AE)=(DB/BC),于是AD •BC+AB •DC=AE •BD+BD •CE=AC •BD例1、(等角共轭点性质)已知 点D E 、在ABC ∆内,ABD CBE ∠=∠,BAE CAD ∠=∠.求证ACD BCE ∠=∠.BCBB证明(一)(文武光华数学工作室南京潘成华)作E关于BC AB AC、、对称点P R Q、、,易知BRD∆≌BPD∆,ARD∆≌AQD∆,于是DP DR DQ==,所以DCP∆≌DCQ∆,得到PCD QCD∠=∠,进而BCE ACD∠=∠.证明(二)作BDS∆外接圆交AD延长线于S,可知ASC DBC ABE∠=∠=∠,得到ABE∆∽ASC∆,所以ABS∆∽AEC∆,得到ACE ASB DSB∠=∠=∠,所以BCE ACD∠=∠.南京潘成华)E是ABC∆内一点,点D在BC上,且BAE DAC∠=∠,EDB ADC∠=∠.则180AEC BED∠+∠=︒证明先证明AB BEAC EC=,过E作AB AC BC、、垂线EF EG EL、、交AB AC BC、、分别于F G L、、,直线EL AD、交于J,取AF中点K,易知B F E L、、、四点共圆,E G C L、、、四点共圆,所以sinsinFLAB C FL CEBEAC B LG LG BECE===⋅(1),(B C、是ABC∆的内角),因为EDB ADC∠=∠,所以EL LJ=,于是//KL AJ,易知A F E G、、、四点共圆,B圆心是K,BAE DAC∠=∠,所以AD FG⊥,进而//KL FG,得到KL是FG中垂线,所以FL LG=,(1)得AB BEAC EC=下面我们证明180AEC BED∠+∠=︒,因为sin sin,ACAEC EACAE∠=∠sin sin,ABBAE BAEBE∠=∠,两式相除得sin sin sinsin sin sinAEC EAC BADBAE BAE DAC∠∠∠==∠∠∠sin sinsin sinAB BAD EC BD EC BEDAC DAC BE CD BE DEC∠∠=⋅=⋅=∠∠,因为360AEC BAE BED DEC∠+∠+∠+∠=︒所以,180AEC BED∠+∠=︒证明(二)在AB取H,使得AHB PDB∠=∠,所以AHD∆∽APC∆,易知H P D B、、、四点共圆,所以180APC BPD BHD AHD∠+∠=∠+∠=︒例3、叶中豪老师2013年国庆讲义一几何题我的解答已知,D是ABC∆底边BC上任一点,P是形内一点,满足12∠=∠,34∠=∠。
第二讲:四点共圆一.有关定理或结论1.共斜边的两个直角三角形的四个顶点共圆,且直角三角形的斜边为圆的直径. 2.共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆. 3.若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆.4.相交弦逆定理:凸四边形ABCD 其对角线AC 、BD 交于P,PD BP PC AP ⋅=⋅⇔四点共圆。
5.割线长定理:凸四边形ABCD 其边的延长线AB 、CD 交于P.PD PC PB PA ⋅=⋅⇔四点共圆。
图3 图4 图5二.证“四点共圆”的基本方法例1.如图1,⊙1o ,⊙2o ,⊙3o … 都经过点A 和B.点P 是线段AB 延长线上任意一点,且PC ,PD ,PE …分别与⊙1o ,⊙2o ,⊙3o …相切于点C,D,E,…。
求证:C,D,E …在同一个圆上。
例2. 如图,在△ABC 中,AD ⊥BC ,DE ⊥AB ,DF ⊥AC .求证:B 、E 、F 、C 四点共圆.例3.如图3,在梯形ABCD 中,AB ∥DC ,AB >CD ,K ,M 分别在AD ,BC 上, ∠DAM =∠CBK.求证:C ,D ,K ,M 四点共圆例4. 如图,E 、F 、G 、H 分别是菱形ABCD 各边的中点.求证:E 、F 、G 、H 四点共圆. AB C D A B C D P A BCD PC图3MK BACD三.四点共圆的应用1. 用于证明两角相等例1.如图,梯形ABCD中AB//DC, 且∠CBN 求证:∠CNB = ∠2.用于证明两条线段相等例2. 已知: 圆O的弦CF、DE交于点B, PB//EF, 交CD的延长线于点P, PA与圆O切于点A.求证: PA=PB .3. 用于证明两直线平行例3 如图3,在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC.4.用于证明两直线垂直5. 用于判定切线例5 如图5,AB为半圆直径,P为半圆上一点,PC⊥AB于C,以AC为直径的圆交PA于D,以BC为直径的圆交PB于E,求证:DE是这两圆的公切线.6. 用于证明比例式例6 AB、CD为⊙O中两条平行的弦,过B点的切线交CD的延长线于G,弦PA、PB分别交CD 于E、F.7. 用于证明平方式例7:已知: 点P是等边⊿ABC外接圆的劣弧BC上任意一点, AP交BC于点D.求证: PA2=AC2+PB•PC.8. 用于解计算题例8如图8,△ABC的高AD的延长线交外接圆于H,以AD为直径作圆和AB、AC分别交于E、F点,EF交 AD于 G,若 AG=16cm,AH=25cm,求 AD的长.。
判断四点共圆的方法嘿,咱今儿就来聊聊判断四点共圆的那些事儿!你说这四点共圆啊,就好像是四个小伙伴要一起玩个特别的游戏。
你看哈,要是这四个点到一个定点的距离相等,那不就像四个小伙伴都被同一种魔力吸引着,这不就共圆了嘛!这就好比是大家都喜欢吃同一种糖果,自然而然就凑到一块儿去了。
还有呢,如果一个四边形的一组对角互补,嘿,那它们也大概率是共圆的啦!这就好像是两个人,一个特别开朗,一个特别内敛,互补得很,不就容易成为好朋友,一起在圆这个“大圈子”里玩嘛!再说说,如果两个三角形有一条公共边,并且这条边上的两个端点对于这两个三角形的外接圆的张角相等,那这四个点也很可能共圆哟!这就好像是有一条路,两边分别有两组人,他们看这条路的角度一样,那他们不就处在一个特别的“圈子”里了嘛。
咱再想想,要是把这四个点放在一个平面上,它们之间有着某种特殊的关联,能让你感觉到它们就是应该在一起,形成一个圆。
就像一家人一样,有着特殊的亲情纽带,紧紧地联系在一起。
比如说,你在解题的时候,突然发现这四个点怎么看怎么觉得它们应该在一个圆上,那你就可以大胆地去验证一下呀!看看是不是符合上面说的那些条件。
这就跟你走在路上,看到一群人,感觉他们很合拍,然后去观察发现他们果然有着共同的爱好或者特点是一个道理。
判断四点共圆可不是一件随随便便的事儿呢,得仔细观察,认真思考。
就像侦探破案一样,从各种蛛丝马迹中找到关键线索,然后得出结论。
你可不能马虎,不然就可能错过重要的信息哦!你想想,要是在几何的世界里,你能熟练地掌握这些判断方法,那遇到相关的问题不就迎刃而解啦?就像你有了一把万能钥匙,啥样的锁都能轻松打开。
所以啊,同学们,好好记住这些方法,多去实践,多去运用。
等你真正掌握了,你就会发现几何的世界是多么的奇妙和有趣!别小看这四点共圆,这里面的学问可大着呢!你还等什么,赶紧去试试吧!判断四点共圆,让你的几何学习更上一层楼!。