数学建模实验 ——曲线拟合与回归分析

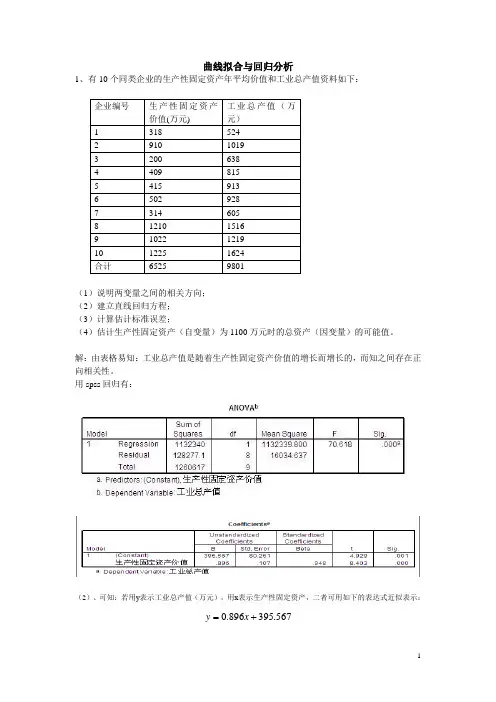
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下：（1）说明两变量之间的相关方向；（2）建立直线回归方程；（3）计算估计标准误差；（4）估计生产性固定资产（自变量）为1100万元时的总资产（因变量）的可能值。

解：由表格易知：工业总产值是随着生产性固定资产价值的增长而增长的，而知之间存在正向相关性。

用spss回归有：（2）、可知：若用y表示工业总产值（万元），用x表示生产性固定资产，二者可用如下的表达式近似表示：=x.0+y.567395896（3）、用spss回归知标准误差为80.216（万元）。

（4）、当固定资产为1100时，总产值可能是（0.896*1100+395.567-80.216~0.896*1100+395.567+80.216）即（1301.0~146.4）这个范围内的某个值。

另外，用MATLAP也可以得到相同的结果：程序如下所示：function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示：b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值（万元）工业总价值（万元）2、设某公司下属10个门市部有关资料如下：（1）、确定适宜的 回归模型； （2）、计算有关指标，判断这三种经济现象之间的紧密程度。

yi )
0
Q(a, b)
b
m
2 (a bxi
i 1
yi )xi
0
整理得到拟合曲线满足的方程：
ma
(
m i 1
xi )b
m i 1
yi
m
m
m
(
i 1
xi )a
(
i 1
xi2 )b
xi yi
i 1
最小二乘算法介绍
上式称为拟合曲线的法方程，可用消元法或者克莱姆方法解得：
m
yi
a i1 m xi yi i1
属性
text text text text Caption Caption Caption Caption Caption Caption Caption Caption Caption Scale Caption Caption Caption
值
自变量的观测值 因变量的观测值
X坐标名称 Y坐标名称 拟合类型 三次样条函数插值 最小二乘法 对数拟合 双曲线拟合 指数拟合
m
xi
i1
m
xi2
i1
m
m
xi
mm
mm
m
m
m
i1 m
( yi xi2 xi xi yi ) (m xi2 ( xi )2
xi
xi2
i1 i1
i1 i1
i1
i1
i1
i1
m
m
m
m
mHale Waihona Puke b (m xi yi xi yi ) (m xi2 ( xi )2 )
i 1
i1 i1
CH3COOC2H5 +Na+ +OH- = CH3 COO- +Na++C2H5OH 设NaOH和CH3COOC2H5 的初始浓度分别为a和b. 当a = b时, 有线性方程

生物医学研究
研究生物标志物与疾病之间的 关系，预测疾病的发生风险。
金融市场分析
分析股票价格、利率等金融变 量的相关性，进行市场预测和 风险管理。
社会科学研究
研究社会现象之间的相关关系 ，如教育程度与收入的关系、 人口增长与经济发展的线性回归模型
线性回归模型是一种预测模型，用于描 述因变量和自变量之间的线性关系。
SPSS实现
SPSS实现步骤 1. 打开SPSS软件； 2. 导入数据；
SPSS实现
01
3. 选择回归分析命令；
02
4. 设置回归分析的变量和选项；
03
5. 运行回归分析；
04
6. 查看并解释结果。
THANKS
感谢观看
回归分析曲线拟合通用课件
• 回归分析概述 • 线性回归分析 • 非线性回归分析 • 曲线拟合方法 • 回归分析的实践应用 • 回归分析的软件实现
01
回归分析概述
回归分析的定义
01
回归分析是一种统计学方法，用 于研究自变量和因变量之间的相 关关系，并建立数学模型来预测 因变量的值。
02
它通过分析数据中的变异关系， 找出影响因变量的主要因素，并 建立回归方程，用于预测和控制 因变量的取值。
线性回归模型的假设包括：误差项的独立性、误差项的同方差性、误差 项的无偏性和误差项的正态性。
对假设的检验可以通过一些统计量进行，如残差图、Q-Q图、Durbin Watson检验等。如果模型的假设不满足，可能需要重新考虑模型的建立 或对数据进行适当的变换。
03
非线性回归分析
非线性回归模型
线性回归模型的局限性
回归分析的分类
01
02
03
一元线性回归

14 0.687 0.691
17 0.64 0.638
27 0.493 0.488
31 0.44 0.439
c=1.003819exp(-0.02669t)
c,t 关系图 1 0.8 0.6 0.4 0.2 0 0 10 20 t 30 40 系列1 系列2
c
c, t¹ Ø Ï µ Í ¼ 1
© ¨mol/L£ c£
0.8 0.6 0.4 0.2 0 0 10 20 t£ ¨min£ ©
3
µ Á Ï Ð 1
30
40
Ⅱ、选 y
1 型试探，将曲线变直，这时 ax b
y=1/cA x=t 算得 1/cA 为：
T 1/cA 2 1.005 5 1.018 8 1.28 1/cA~ t 数表 11 14 1.335 1.445 17 1.568 27 2.028 31 2.273 35 2.507
1
在某液相反应中，不同时间下测的某组成的浓度见下表， 试作出其经验方程。 浓度随时间的变化关系 2 5 8 11 14 17 27 31 时间 t(min) 浓度 cA 0.948 0.879 0.813 0.749 0.687 0.640 0.493 0.440 (mol/L)
35 0.391
Ⅰ、首先将实验数据 t~cA 作图，图像表明，这是一条曲线，不是 y=a+bx 型直线，因此，对照样板曲线重新选型。
lnc， lnt 关系图 0 -0.2 0 1 2 3 4
lnc
-0.4 -0.6 -0.8 -1 lnt 系列1
作 lnc ~lnt 的图，发现原来的曲线不但没变直，反而更加弯曲了。说明这 个类型的经验公式更不适合了。
Ⅳ、又重新选型，选用 y=aebx 型，再试探 y=lncA x=t

beta = 21.0058 19.5285
所以：养护日期 x(日)及抗压强度 y(kg/cm2)的回归方程：y=21.0050+19.5288ln(x)
(2)、主程序如下： x=[2 3 4 5 7 9 12 14 17 21 28 56]; y=[35 42 47 53 59 65 68 73 76 82 86 99]; beta0=[1 1]'; [beta,r,J]=nlinfit(x',y','volum',beta0); beta
(3)、输出结果：
实验目的 1、直观了解回归分析基本内容。 2、掌握用数学软件求解回归分析问题。 实验内容 1、回归分析的基本理论。 2、用数学软件求解回归分析问题。
程序设计
1、考察温度 x 对产量 y 的影响，测得下列 10 组数据：
温度（℃） 20 25 30
35
40
45
50
55
60
65
产量（kg） 13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3
差的置信区间均包含零点，这说明回归模型 y=9.1212+0.2230x 能较好的符合原 始数据，没有异常点.
（5）、预测及作图： z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r')
预测 x=42℃时产量的估值.y=18.4872
2、某零件上有一段曲线，为了在程序控制机床上加工这一零件，需要求这段曲 线的解析表达式，在曲线横坐标 xi 处测得纵坐标 yi 共 11 对数据如下：
s=[0.6 2.0 4.4 7.5 11.8 17.1 23.3 31.2 39.6 49.7 61.7];

曲线拟合摘要根究已有数据研究y关于x的关系，对于不同的要求得到不同的结果。

问题一中目标为使的各个观察值同按直线关系所预期的值的偏差平方和为最小，利用MATLAB中tlsqcurvefi函数在最小二乘法原理下拟合出所求直线。

问题二目标为使绝对偏差总和为最小，使用MATLAB中的fminsearch函数，在题目约束条件内求的最优答案，以此方法同样求得问题三中最大偏差为最小时的直线。

问题四拟合的曲线为二阶多项式，方法同前三问类似。

问题五为求得最佳的曲线，将之前的一次曲线换成多次曲线进行拟合得到新的结果。

经试验发现高阶多项式的阶数越高拟和效果最好。

)关键词：函数拟合最小二乘法线性规划|<￥一、问题的重述已知一个量y 依赖于另一个量x ，现收集有数据如下：（1）求拟合以上数据的直线a bx y +=。

目标为使y 的各个观察值同按直线关系所预期的值的偏差平方和为最小。

（2）求拟合以上数据的直线a bx y +=，目标为使y 的各个观察值同按直线关系所预期的值的绝对偏差总和为最小。

（3）求拟合以上数据的直线，目标为使y 的各个观察值同按直线关系所预期的值的最大偏差为最小。

（4）求拟合以上数据的曲线a bx cx y ++=2，实现（1）（2）（3）三种目标。

}（5）试一试其它的曲线，可否找出最好的？二、问题的分析对于问题一，利用MATLAB 中的最小二乘法对数据进行拟合得到直线，目标为使各个观察值同按直线关系所预期的值的偏差平方和为最小。

对于问题二、三、四均利用MATLAB 中的fminsearch 函数，在题目要求的约束条件下找到最佳答案。

对于问题五，改变多项式最高次次数，拟合后计算残差，和二次多项式比较，再增加次数后拟合，和原多项式比较残差，进而找到最好的曲线。

~三、基本假设1.表中数据真实可信，每个点都具有意义。

四、模型的建立与求解1.问题一 ：对给定数据点(){}),,1,0(,m i Y X i i =，在取定的函数类Φ 中，求()Φ∈x p ，使误差的平方和2E 最小，()[]22∑-=i i Y X p E 。

回归分析
一、变量之间的两种关系 1、函数关系：y = f (x) 。
2、相关关系：X ，Y 之间有联系，但由 其中一个不能唯一的确定另一个的值。 如： 年龄 X ，血压 Y ； 单位成本 X ，产量 Y ； 高考成绩 X ，大学成绩 Y ； 身高 X ，体重 Y 等等。
二、研究相关关系的内容有
1、相关分析——相关方向及程度（第九章）。 增大而增大——正相关； 增大而减小——负相关。 2、回归分析——模拟相关变量之间的内在 联系，建立相关变量间的近似表达式 （经验 公式）（第八章）。 相关程度强，经验公式的有效性就强， 反之就弱。
三、一般曲线性模型 1、一般一元曲线模型
y = f ( x) + ε
对于此类模型的转换，可用泰勒展开 公式，把 在零点展开，再做简单的变 f ( x) 换可以得到多元线性回归模型。 2、一般多元曲线模型
y = f ( x1 , x2源自,⋯ , xm ) + ε
对于此类模型也要尽量转化为线性模 型，具体可参考其他统计软件书，这里不 做介绍。
ˆ ˆ ˆ ˆ y = b0 + b1 x1 + ⋯ + bm x m
2、利用平方和分解得到 ST , S回 , S剩。 3、计算模型拟合度 S ，R ，R 。 （1）标准误差（或标准残差）
S =
S剩 ( n − m − 1)
当 S 越大，拟合越差，反之，S 越小， 拟合越好。 （2）复相关函数
R =
2
仍是 R 越大拟合越好。 注： a、修正的原因：R 的大小与变量的个数以及样本 个数有关； 比 R 要常用。 R b、S 和 R 是对拟合程度进行评价，但S与 R 的分 布没有给出，故不能用于检验。 用处：在多种回归模型（线性，非线性）时， 用来比较那种最好；如：通过回归方程显著性检验 得到：

2、多项式回归
设变量 x、Y 的回归模型为 Y 0 1x 2 x2 ... p x p
其中 p 是已知的，i (i 1,2,, p) 是未知参数， 服从正态分布 N (0, 2 ) .
Y 0 1x 2 x2 ... k xk
腿长
88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102
以身高x为横坐标，以腿长y为纵坐标将这些数据点（xI，yi） 在平面直角坐标系上标出.
解答
102
100
98
y 0 1x
96
949290 Nhomakorabea88
86
84
140
145
150
155
160
165
2019/7/8
17
二、模型参数估计
1、对 i 和 2 作估计
用最小二乘法求0 ,..., k 的估计量：作离差平方和
n
Q yi 0 1xi1 ... k xik 2 i 1
选择 0 ,..., k 使 Q 达到最小。
解得估计值 ˆ
进行检验.
假设 H 0 : 1 0 被拒绝，则回归显著，认为 y 与 x 存在线性关 系，所求的线性回归方程有意义；否则回归不显著，y 与 x 的关系 不能用一元线性回归模型来描述，所得的回归方程也无意义.
2019/7/8
8
（Ⅰ）F检验法
当 H 0 成立时，
F
U
~F（1，n-2）
Qe /(n 2)
变量的值 x1* ,..., xk ，用 yˆ * ˆ0 ˆ1 x1* ... ˆk xk * 来预测

A=polyfit(x,y,2)
%做出数据点和拟合曲线的图形
z=polyval(A,x);
plot(x,y,'k+',x,z,'r')
h=(y-z).^2;
disp('抛物线拟合函数的残差平方和')
Q=[1 1 1 1 1 1 1 1 1 1]*h'
A = 0.4356 -9.3114 74.3258
A=polyfit(1./x,y,1)
%做出数据点和拟合曲线的图形
z=polyval(A,1./x);
plot(1./x,y,'k+',1./x,z,'r')
A =87.3300 18.1604
五、实验心得（质疑、建议）：
A =-8.0803 17.9488 0.5429
3.
x=[2 3 4 5 6 7 8 9 10 11];
y=[58 50 44 38 34 30 29 26 25 24];
A=polyfit(x,y,1)
%做出数据点和拟合曲线的图形
z=polyval(A,x);
plot(x,y,'k+',x,z,'r')
湖南第一师范学院数学系实验报告
姓名：
学号：
专业：
数学与应用数学
班级：
课程名称：
线性规划与数学建模
实验名称：
曲线拟合
实验类型：
基础实验
实验室名称：
实验地点：
实A302
实验时间：
2016年5月17日
指导教师：
成绩评定：
一、实验目的与要求：
1、了解曲线拟合基本原理。

编号 1 2 3 4 5 6 7 8 身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172cm的女大学生的体重。
解：1、选取身高为自变量x，体重为因变量y，作散点图：
由于解释变量和随机误差的总效应（总偏差平方和）为354，而随机误差的效应为 128.361，所以解析变量的效应为
354-128.361=225.639 这个值称为回归平方和。
解析变量和随机误差的总效应（总偏差平方和） =解析变量的效应（回归平方和）+随机误差的效应（残差平方和）
我们可以用相关指数R2来刻画回归的效果，其计算公式是
R2越接近1，表示回归的效果越好（因为R2越接近1，表示解释变量和预报变量的 线性相关性越强）。
如果某组数据可能采取几种不同回归方程进行回归分析，则可以通过比较R2的值 来做出选择，即选取R2较大的模型作为这组数据的模型。
总的来说：
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中，它代表自变量刻画预报变量的能力。
虽然这种向中心回归的现象只是特定领域里的结论，并不具有普遍性，但从它 所描述的关于X为自变量，Y为不确定的因变量这种变量间的关系看，和我们现在的 回归含义是相同的。
不过，现代回归分析虽然沿用了“回归”一词，但内容已有很大变化，它是一种应用 于许多领域的广泛的分析研究方法，在经济理论研究和实证研究中也发挥着重要作用。
回归分析：研究一个随机变量Y对另一个(X)或一组(X1， X2，…，Xk)变量的相依关系的统计分析方法
回归分析（regression analysis)是确定两种或两种以上变数 间相互依赖的定量关系的一种统计分析方法。运用十分广泛， 回归分析按照涉及的自变量的多少，可分为一元回归分析和 多元回归分析；按照自变量和因变量之间的关系类型，可分 为线性回归分析和非线性回归分析。如果在回归分析中，只 包括一个自变量和一个因变量，且二者的关系可用一条直线 近似表示，这种回归分析称为一元线性回归分析。如果回归 分析中包括两个或两个以上的自变量，且因变量和自变量之 间是线性关系，则称为多元线性回归分析。

数据拟合与回归分析数据拟合和回归分析是统计学和数据分析中常用的方法，用于建立变量之间的关系并预测未知值。

在本文中，我将介绍数据拟合和回归分析的基本概念、方法和应用。

数据拟合是指找到一个函数或曲线，使其最好地描述已知数据的分布。

这个函数或曲线被称为拟合函数。

拟合函数的选择取决于数据类型和问题的特点。

例如，对于线性关系，可以使用线性拟合，即拟合函数是一个直线。

对于非线性关系，可以使用多项式、指数、对数等函数形式。

回归分析是根据已知数据建立一个模型，用来描述变量之间的关系，并预测未知值。

回归分析的目标是找到一个最佳拟合模型，使其尽量准确地预测未知值。

回归分析通常包括以下步骤：收集数据、确定模型类型、拟合模型、评估模型、预测未知值。

数据拟合和回归分析在许多领域中都有广泛的应用。

例如，在经济学中，回归分析可以用来研究变量之间的关系，如收入和消费之间的关系。

在医学研究中，回归分析可以用来预测疾病的发展和治疗效果。

在市场营销中，回归分析可以用来预测产品销售量和推广效果。

在进行数据拟合和回归分析时，需要注意以下几点。

首先，数据的质量对于拟合和预测的准确性至关重要。

因此，需要对数据进行筛选、清洗和处理，以去除错误、异常值和缺失值。

其次，选择适当的拟合函数和模型类型对于获得准确的拟合和预测结果至关重要。

这需要根据数据类型和问题特点进行选择和调整。

最后，对拟合和预测结果进行评估和解释是非常重要的。

评估方法可以包括残差分析、检验假设等。

总之，数据拟合和回归分析是统计学和数据分析中常用的方法，用于建立变量之间的关系和预测未知值。

它们在许多领域中有广泛应用，如经济学、医学研究、市场营销等。

在进行数据拟合和回归分析时，需要注意数据质量、选择适当的拟合函数和模型类型，并对结果进行评估和解释。

通过合理使用数据拟合和回归分析，我们可以更好地理解变量之间的关系，并做出准确的预测和决策。

曲线拟合与回归分析1、有 10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1说明两变量之间的相关方向;(2建立直线回归方程;(3计算估计标准误差;(4估计生产性固定资产(自变量为 1100万元时的总资产(因变量的可能值。

解:(1工业总产值是随着生产性固定资产价值的增长而增长的,存在正向相关性。

用 spss 回归(2 spss 回归可知:若用 y 表示工业总产值(万元,用 x 表示生产性固定资产,二者可用如下的表达式近似表示:567.395896. 0+=xy(3 spss 回归知标准误差为 80.216(万元。

(4当固定资产为 1100时,总产值为:(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216 即(1301.0~146.4这个范围内的某个值。

MATLAB 程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x', x'];[b,bint,r,rint,stats] = regress(y',X,0.05;display(b;display(stats;x1 = [300:10:1250];y1 = b(1 + b(2*x1;figure;plot(x,y,'ro',x1,y1,'g-';生产性固定资产价值 (万元工业总价值 (万元industry = ones(6,1; construction = ones(6,1; industry(1 =1022; construction(1 = 1219; for i = 1:5industry(i+1 =industry(i * 1.045;construction(i+1 = b(1 + b(2* construction(i+1; enddisplay(industry; display( construction; end运行结果:b = 395.5670 0.8958 stats = 1.0e+004 *0.0001 0.0071 0.0000 1.6035 industry = 1.0e+003 * 1.0220 1.0680 1.1160 1.16631.2188 1.2736 construction = 1.0e+003 * 1.2190 0.3965 0.3965 0.3965 0.3965 0.3965。

n-2
21 22 23 24 25 26 27 28 29 30
0.05 0.01
0.413 0.404 0.396 0.388 0.381 0.374 0.367 0.364 0.355 0.349
0.526 0.515 0.505 0.496 0.487 0.478 0.470 0.463 0.456 0.449
单击此处添加大标题内容
04
05
从偏回归平方和的意义可以看出,凡是对Y作用显著的因素一般具有较大的Ｐi值。Ｐi愈大,该因素对Y的作用也就愈大,这样通过比较各个因素的Pｉ值就可以大致看出各个因素对因素变量作用的重要性。在实用上,在计算了偏回归平方和后,对各因素的分析可以按下面步骤进行:
01
为此,我们要先计算
腐蚀时间x（秒）
腐蚀深度y（μ）
5 5 10 20 30 40 50 60 65 90 120
4 6 8 13 16 17 19 25 25 29 46
40 30 20 10
y
x
10 20 30 40 50 60 70 80 90 100 110 120
只有当正规方程的系数矩阵为对角型
在化工实验数据处理中，我们经常会遇到这样的问题，即已知两个变量之间存在着函数关系，但是，不能从理论上推出公式的形式，要我们建立一个经验公式来表达这两个变量之间的函数关系。
01Leabharlann 二元溶液的溶解热与浓度的函数关系
02
反应物的浓度与反应时间的函数关系
03
做散点图，选经验方程，曲线变直，相关系数对比，求出常数
相关系数临界值表
预报与控制
01
当我们求得变量x、y之间的回归直线方程后，往往通过回归方程回答这样两方面的问题：

数据点集(x1,y1),…,(xn,yn)最小二乘直线方程 y=a+bx 将所有点代入直线方程后相加，我们得到 y=an+bx(或 y a b x) 以及 xy=ax+bx2 这两个方程称为最小二乘的正规方程。由上 面的方程组我们可以达到a,b分别为：
yx xxy a , 2 2 n x ( x ) nxy xy b , 其中b也可以写成 2 2 n x ( x )
1 1 0 z ln( ), z 2 1 0
1 n3
z
1
2
这里
Z Z Z Z , Z Z
1 2 1 2 1 2
2 1
2 2
1 1 n1 3 n2 3
是近似正态分布。
回归的概率解释
从同一总体抽取不同的样本作拟合，我们会 得到不同的回归曲线。 给定两个随机变量X和Y的联合密度函数和概 率函数。如果使E{[Y-g(X)]2}=最小值的y=g(x) 曲线称为Y关于X的最小二乘回归曲线有如下 定理： 定理一：y=g(x)=E(Y|X=x)满足E{[Y-g(X)]2}= 最小值，所以它是Y关于X的最小二乘曲线。
定理二：如果X和Y是具有二元正态分布的随机变量， 那么Y关于X的最小二乘回归曲线是一条回归直线，为
y Y
Y
(
x X
X
)
这里
XY ＝ XY
前面对样本的最小二乘回归的叙述容易推广到总体上。 例如，总体情况下的估计的标准误差用方差和相关系数 2 2 2 ( 1 ) 项给定为 Y . X Y
曲线拟合、回归和相关
曲线拟合
实践中寻求两个(或多个) 变量间存在的关系，拟 合给定数据用以确定变 量间的近似曲线方程， 此过程叫曲线拟合。

如何在报告中准确解读回归与拟合曲线一、回归分析的基本原理和概念1.1 回归分析的定义和应用领域1.2 简单线性回归与多元线性回归的区别1.3 回归分析中的相关系数和确定系数的含义二、回归线的解读2.1 回归线的方程及参数估计2.2 利用回归线进行预测和精确度评估2.3 回归线的显著性检验和解释三、拟合曲线的解读3.1 拟合曲线的定义和建立方法3.2 拟合曲线的优度评估指标3.3 拟合曲线中的过拟合与欠拟合问题四、误差项的解读4.1 误差项的定义和性质4.2 常见的误差分布假设4.3 残差分析和异常值的处理五、多元回归的解读5.1 多元回归模型的基本构建和参数估计5.2 多元回归模型的显著性检验和系数解释5.3 多重共线性和变量选择的问题六、回归与拟合曲线的应用案例解析6.1 金融领域中的回归分析应用6.2 生物医学中的拟合曲线应用6.3 工程领域中的多元回归分析案例回归分析在统计学和数据分析中被广泛应用，用于探究变量之间的关系和预测未来趋势。

在报告中准确解读回归与拟合曲线是非常重要的，能够帮助读者对数据进行深入理解和正确的应用。

本文将从回归分析的基本原理和概念开始，逐步展开，通过六个小标题进行详细论述。

首先，我们需要了解回归分析的基本原理和概念。

回归分析是一种用于研究因变量与一个或多个自变量之间关系的统计方法。

在不同的应用领域中，回归分析有着广泛的应用，比如金融领域的股市预测和走势分析，生物医学领域的药物疗效评估等。

同时，我们还介绍了简单线性回归和多元线性回归的区别，以及回归分析中使用的相关系数和确定系数的含义。

接下来，回归线的解读是非常重要的一环。

我们介绍了回归线的方程及参数估计的方法，以及如何利用回归线进行预测和精确度评估。

此外，还需要进行回归线的显著性检验和解释，以确定回归模型是否具有统计学意义。

在拟合曲线的解读中，我们首先介绍了拟合曲线的定义和建立方法，说明了拟合曲线的优度评估指标。

同时，我们讨论了拟合曲线中的过拟合与欠拟合问题，这对于解读拟合曲线的准确性和稳定性有着重要意义。