【信号与系统(郑君里)课后答案】第七章习题解答
- 格式:docx
- 大小:193.16 KB
- 文档页数:4

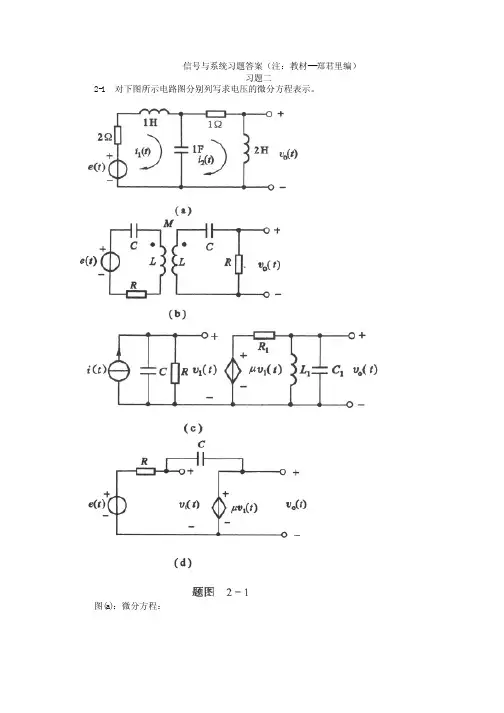
15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5-1(a)所示。
)()2(n x 序列的图形如图5-1(b)所示。
)()3(n x 序列的图形如图5-1(c)所示。
)()4(n x 序列的图形如图5-1(d)所示。
)()5(n x 序列的图形如图5-1(e)所示。
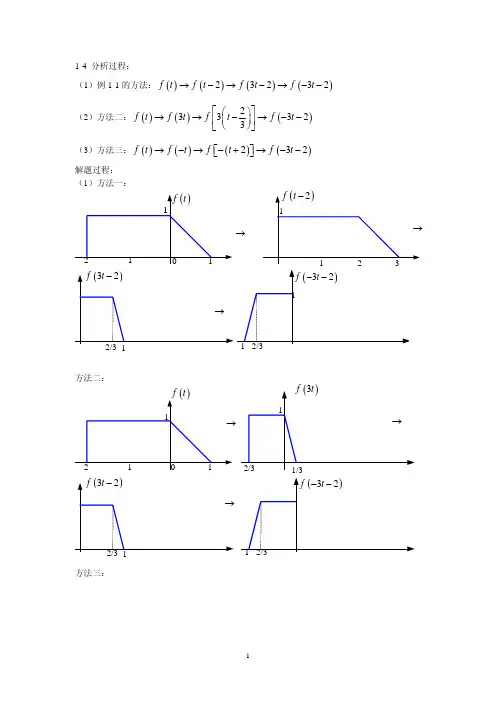
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5-2(b)所示。
x()2(n 序列的图形如图5-2(c)所示。
x))3(n(x 序列的图形如图5-2(d)所示。
)4(n())5(n 序列的图形如图5-2(e)所示。
x()x 序列的图形如图5-2(f)所示。
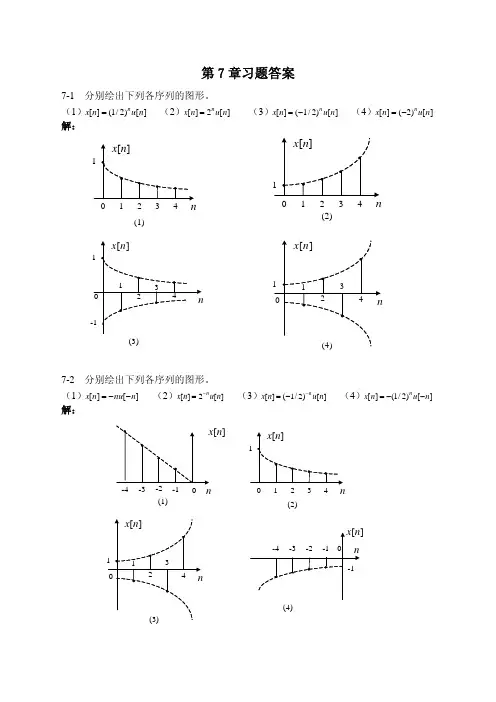
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-3(a)所示。
)()2(n x 序列的图形如图5-3(b)所示。
)()3(n x 序列的图形如图5-3(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的,如果是周期性的,试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数,所以)(n x 是周期性的,且周期为14。


信号与系统第三版郑君里课后习题答案第一章习题参考解1,判刑下列信号的类型解:()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。
()(2y n x n =) 离散、模拟、非周期、功率型信号。
()()y n n x n = 离散、模拟、非周期、功率型信号。
1-6,示意画出下列各信号的波形,并判断其类型。
(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数,不是物理量。
(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1-6题,1-4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1-6 5-6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1-8,判断下列系统的类型。


信号与系统课后答案:郑君里第7章简介本文是《信号与系统》课程的第7章课后答案,该章节由著名作者郑君里所撰写。
本章主要介绍了信号与系统的离散傅里叶变换(DFT)和离散时间傅里叶变换(DTFT)。
信号处理是一门研究如何用数学方法描述和处理各种信号的科学。
信号是信息的载体,而系统是对信号进行处理的载体。
离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一,它们具有广泛的应用。
理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。
第7章课后题答案第1题根据定义,离散傅里叶变换(DFT)的计算公式如下:$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中,N表示信号的长度,N(N)表示输入信号的离散采样值,N(N)表示变换结果中的频谱系数。
根据公式,我们可以计算出给定信号的DFT变换。
第2题离散傅里叶变换的逆变换公式如下:$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。
第3题离散时间傅里叶变换(DTFT)的计算公式如下:$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示,它不仅适用于周期信号,也适用于非周期信号。
第4题DTFT的逆变换公式如下:$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。
第5题离散时间傅里叶变换的频谱无法在计算机中实现,因为DTFT变换结果是连续的函数。


目 录第一部分 名校考研真题第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第二部分 课后习题第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第三部分 章节题库第7章 离散时间系统的时域分析第8章 z变换、离散时间系统的z域分析第9章 离散傅里叶变换以及其他离散正交变换第10章 模拟与数字滤波器第11章 反馈系统第12章 系统的状态变量分析第四部分 模拟试题第一部分 名校考研真题 说明:本部分从指定郑君里主编的《信号与系统》(第3版)为考研参考书目的名校历年考研真题中挑选最具代表性的部分,并对其进行了详细的解答。
所选考研真题既注重对基础知识的掌握,让学员具有扎实的专业基础;又对一些重难点部分(包括教材中未涉及到的知识点)进行详细阐释,以使学员不遗漏任何一个重要知识点。
第7章 离散时间系统的时域分析一、填空题1.周期分别为3和5的两个离散序列的卷积和的周期性为______。
[北京航空航天大学2007研]【答案】7【解析】对于线性卷积,若一个周期为M,另一个周期为N,则卷积后周期为M+N-1,所以。
2.某线性时不变(L TI)离散时间系统,若该系统的单位阶跃响应为则该系统的单位脉冲响应为______。
[北京交通大学研]【答案】【解析】本题考查离散时间系统的单位脉冲响应。
用表示单位阶跃响应,由于利用线性和时不变特性可得二、判断题一个离散时间信号实际上就是一组序列值的结合{x(n)}。
( )[南京大学2010研]【答案】√【解析】离散时间函数,只有在某些离散时给出函数值,只是在某些离散瞬时给出函数值。
因此,它是时间不连续的“序列”的。
三、选择题1.信号的周期是( )。
