画法几何及工程制图第二章相对位置

h
2、过直线EF作正垂
e 平面P。
3、求平面P与平面 KMN的交线ⅠⅡ。
he
4、求交线ⅠⅡ 与 EF的交点H。
5、连接KH，KH即 为所求。
k
27
2-3 垂直问题
2.3.1 直线与平面垂直 2.3.2 平面与平面垂直
28
2.3.1 直线与平面垂直
V
C A
E BDΒιβλιοθήκη H 几何条件：若一直线垂直于一平面，则必垂直于属于该 平面的一切直线。
求解综合问题主要包括：空间几何元素的定位问 题（交点、交线）和空间几何元素的度量问题（如 距离、角度）。
综合问题解题的一般步骤： 1. 分析题意 2. 明确所求结果，找出解题方法 3. 拟定解题步骤
43
2.4.1 空间几何元素定位问题
例14 已知三条直线CD、EF和GH，求作一直线AB与CD平
行，并且与EF、GH均相交。
38
A
Ⅰ Ⅱ
B
两平面垂直
A
Ⅰ
B
Ⅱ
两平面不垂直
反之，两平面相互垂直，则由属于第一个平面的任意一点 向第二个平面作的垂线必属于第一个平面。
39
例12 平面由 BDF给定，试过定h点K作已知平面的垂面
f
c
g
k
a
b
d
X
a d
f c
O k
g
b h
40
例13 试判断 ABC与相交两直线KG和KH所给定的平面是否
24
例7 试过K点作一直线平行于已知平面ΔABC，并与直线EF相 交。
b
X
b
c f
a
a f
k
e
eO

第二章点、直线、平面的投影————点的投影班级学号姓名. 学习帮手.第二章点、直线、平面的投影————点的投影班级学号姓名. 学习帮手.13 第二章点、直线、平面的投影————点的投影班级学号姓名. 学习帮手.14 第二章点、直线、平面的投影————直线的投影班级学号姓名. 学习帮手.15 第二章点、直线、平面的投影————直线的投影班级学号姓名. 学习帮手.16 第二章点、直线、平面的投影———直线的实长班级学号姓名. 学习帮手.. 学习帮手.17 第二章点、直线、平面的投影———直线的实长班级学号姓名. 学习帮手.18 第二章点、直线、平面的投影———直线上的点班级学号姓名. 学习帮手.19 第二章点、直线、平面的投影———两直线的相对位置班级学号姓名. 学习帮手.. 学习帮手.20 第二章点、直线、平面的投影———直线的相对位置班级学号姓名. 学习帮手.. 学习帮手.21第二章点、直线、平面的投影———两直线的相对位置班级学号姓名. 学习帮手.. 学习帮手.22 . 学习帮手.第二章点、直线、平面的投影———两直线的相对位置班级学号姓名. 学习帮手.23第二章点、直线、平面的投影———两直线的相对位置班级学号姓名. 学习帮手.24第二章点、直线、平面的投影———两直线的相对位置班级学号姓名. 学习帮手.25第二章点、直线、平面的投影——平面的投影班级学号姓名. 学习帮手.. 学习帮手 .26第二章 点、直线、平面的投影——平面的投影 班级 学号 姓名A 面是 正垂面B 面是水平面C 面是 侧平面A 面是 水平面B 面是 圆柱面C 面是 正平面A 面是侧平面 。

B 面是 正平面 C 面是 水平面. 学习帮手 .27第二章 点、直线、平面的投影——平面的投影 班级 学号 姓名A 面是 圆柱面B 面是 水平面A 面是 正平面A 面是 侧垂面 。

B 面是 水平面 。

. 学习帮手.28第二章点、直线、平面的投影——平面的投影班级学号姓名. 学习帮手.. 学习帮手.29第二章点、直线、平面的投影——平面的投影班级学号姓名2-56 完成下列平面的两面投影。

直线、平面的相对位置关系教学目的要求：研究直线与平面以及平面与平面的相对位置关系在投影图中的投影特性和基本作图方法。

包括：平行、相交和垂直。

教学重点难点：相交关系的作图方法与步骤，及可见性的判断，线、面相对位置综合作图。

学时：3§ 1平行关系1．1直线与平面平行几何条件：如果平面外的一直线和这个平面上的一直线平行，则此直线平行于该平面，反之亦然。

投影：如果直线的投影与平面内任意一直线的同面投影平行，在空间则直线与平面平行。

根据此定理，我们可以在投影图上判断直线与平面是否平行，并解决直线与平面平行的作图问题。

作图：如图5-1所示，已知b’d’∥e’f’,bd∥ef,且BD是ABC平面上的一直线，因此，直线BD∥ΔABC。

图5-1例1：过点K作一水平线，使之平行于ΔABC（图5-2）解：①在ΔABC上作一水平线AD。

（先作正面投影 aˊdˊ∥X）②过K点作直线KL∥AD。

（kl∥ad，kˊlˊ∥aˊdˊ）直线KL即为所求。

图5-2例2：过点K作一铅垂面（用迹线表示），使之平行于直线AB解：由于铅垂面的H投影为一直线，所以作铅垂面平行于直线AB，则P H必平行于ab。

1）过k作P H∥ab,与X轴交于P X点。

2）过P X点作P V⊥X轴，则P平面即为所求。

图5-31.2平面与平面平行几何条件：如果一平面上的两条相交直线分别平行于另一平面上的两条相交直线，则此两平面平行。

投影：一个平面内任意两条直线的投影分别与另一个平面内两条相交直线的同面投影对应平行，则这两个平面平行。

作图：由于AB∥A1B1,BC∥B1C1,所以平面ABC∥平面A1B1C1，如图5-4所示图5-4两平行平面的同面迹线一定平行，反之，如果两平面的两对同面迹线分别相互平行，则不能确定两平面是相互平行的。

在图5-5中两平面平行，在图5-6中两平面不平行。

图5-5图5-6§2相交关系求直线与平面的交点和两平面的交线是解决相交问题的基础。

▪ 在投影图上判断两点的相对位置关系
Z
a’
a”
H 面上：左右，前后
b’
X
O
a b
b” V 面上：左右，上下 W 面上：上下，前后
YW
B 点在A 点的左、
前、下方
YH
§2-4 点的相对位置
二、重影点
定义：在同一条投射线上的两点，其在某投影面上的
投影重合，称这两点为该投影面的重影点。
A、B 为H 面上的重影点。
V a’
Z
a’
Z a”
b’ A
B X
a” O b”
b’ X
b” O
YW
a ( b)
Y a( b)
YH
水平投影重影，由正(侧)面投影判断上下关系。
§2-4 点的相对位置
二、重影点
C、D 为V面上的重影点。
Z
V
c’( d)’
c(’ d)’
D
d”
C O
c” X
ห้องสมุดไป่ตู้
X d
d
c
Yc
Z d” c”
O YW
YH
正面投影重影，由水平(和侧面)投影判断前后。
一、两点相对位置的判断方法
▪ 空间两点的相对位置，可以通过两点的同组投影
判断其前后、上下、左右关系。
V
b’
X
左右
Z 上 约定:
a’ A
下 X 轴方向 称 左右
a”
Y 轴方向 称 前后
Z 轴方向 称 上下
B
O
a b
b”
后 B 点在A 点的 前 左、前、下方
Y
§2-4 点的相对位置
一、两点相对位置的判断方法

第五页，共43页。
第二章 直线
5
§2—2 直线上的点
迹点投影的两个特征：
1.迹点所在投影面上的投影
就是迹点本身，即Mm、Nn′、 Ss″；
2.迹点的其他投影必在直 线的相应投影与投影轴的相交
处，即m′在OX轴上，m″在OY 轴上（因zm=0）；n在OX轴上， n″在OZ轴上（因yn=0）；s 在OY轴上，ｓ′在OZ轴上（因 xs=0）。
α有 倾角 β= 0° 迹点
γ=有
M有
N有
S无
第十九页，共43页。
第二章 直线
19 19
§2—5 两直线的相对位置
有三种情况：平行、相交、交错（交叉）
相交
平行
交错
第二十页，共43页。
20
第二章 直线
20
§2—5 两直线的相对位置
一、两直线平行
空间平行的两直线，其所有的同面投影彼此平行.
反之，若三面体系中两直线的所有同面投影都平行，则空间两直 线平行。
倾斜态，并非直线的远近、上下、左右、前 后等线性度量关系。
铅垂线
投影面垂直线 正垂线 侧垂线
水平线
投影面平行线 正平线
侧平线
一般位置直线
第十一页，共43页。
11
第二章 直线
11
§2—4 各种位置直线的投影
二、特殊位置直线的投影特征
投影面垂直线和投影平行线，统
称为特殊位置直线。
投影面垂直线的投影特征:
第九页，共43页。
第二章 直线
9
§2—3 直线的倾角和直线段的实长
例2-2 已知直线CD的正面
投影c′d′和点C的水平 投影c，且知直线CD对H面
的 倾 角 α=30° ， 求 作 线

平面投影的实际应用
PRT SIX
建筑制图的投影应用
建筑平面图：表示建筑物的平面形状和尺寸
建筑立面图：表示建筑物的立面形状和尺寸
建筑剖面图：表示建筑物的剖面形状和尺寸
建筑详图：表示建筑物的细部构造和尺寸
工程制图的投影应用
建筑设计：绘制建筑平面图、立面图、剖面图等
机械设计：绘制机械零件图、装配图等
,
画法几何制图—平面的投影及相对位置
目录
Prt One
添加目录标题
Prt Two
平面投影的基本概念
Prt Three
平面投影的特性
Prt Four
平面间的相对位置关系
Prt Five
平面与投影面间的相对位置关系
Prt Six
平面投影的实际应用
添加章节标题
PRT ONE
平面投影的基本概念
PRT TWO
平面的表示方法
投影面：将物体投影到平面上形成平面图形
投影线：连接物体与投影面的直线
投影点：物体与投影面的交点
投影方向：投影线与投影面的夹角
投影面法线：垂直于投影面的直线
投影面坐标：表示平面图形在投影面上的位置和方向
投影面与平面的关系
投影关系：物体与投影面之间的相对位置关系
投影面：将物体投影到平面上形成投影面
特点：平面与投影面之间没有交点且平行于投影面
垂直关系
垂直关系：平面与投影面之间的一种相对位置关系
垂直关系特点：平面与投影面之间的夹角为90度
垂直关系应用：在工程制图中垂直关系常用于表示物体的高度、宽度和深度
垂直关系判断：通过测量平面与投影面之间的夹角判断是否满足垂直关系
倾斜关系
倾斜角度：平面与投影面之间的夹角

[例2] 已知点A(6,3,4),B点在A点的右、前、上方各2个
的投影
单位，C点在B点的正下方3个单位，求各点的投影。
b
a c
2
X
6
2
3
Z
4
a"
0
b" c"
YW
a b (c)
2
3
YH
[ ]
[例3] 已知点A(10,15,20),点B距W、V、H面分别为20mm、 影投的点求 3例 10mm、15mm，点C在点A之左15mm，之前5mm、 之下10mm，求各点的投影。
点A到W面的距离为：
Aa"=a’az=aayH =X坐标；
点A到V面的距离为：
Aa’=a"az=aax =Y坐标；
点A到H面的距离为：
Aa=a"ayW=a’ax=Z坐标；
Z A到W面
A到V面 Va' aZ
距离
距离
A
A到H面X ax
O
a" W
距离
a
aY
H
Y
A到W面
距离 Z
点的H面投影反映点的X、Y坐标；
水平投影面（水平面、H面） 正立投影面（正面、V面） 投影轴：X轴。
四个分角：H、V两投影面将空间划分为四个分角。
A点的投影：H面投影a , V面投影a’。
投影面的展开：V面不动，H面绕X轴向下旋转与V面重合。
实际画图不画外框线
Ⅱ Ⅰ
Ⅲ Ⅳ
a' V
X X ax H
a
V第
Ⅰ
A
分
角
aH H
V a'
X ax
a H

1(2) 3 4
e k l f a b b l f a
d
X
d
g g
3(4)
2 k c 1 e
利 用 重 影 点 判 别 可 见 性
35
垂直问题
三、垂直问题
m k
e
c
f
d
1.直线与平面垂直 a
X
b
a
e
k
f d
c
m
b
直线与平面垂直，则直线 垂直平面上的任意直线。
X
a
b a
c Y
b
YV
YH 投影特性： (1) abc、 abc重影为一条线，具有积聚性 (2) 水平投影 abc反映 ABC实形 9
c
正平面
b' a' B A C c b a Y Z
b' b"
a" c' X c b a a'
Z
b" a" c" YV
c'
X
c"
YH
投影特性： (1) abc 、 abc 重影为一条线，具有积聚性 (2) 正平面投影 abc反映 ABC实形
反之，直线垂直平面上 的任意两条相交直线，则直 线垂直该平面。
36
垂直问题
分析：
[例题一]求点C到直线AB的距离。 a
过C点作一平面与直线AB垂 直，求出平面与AB的交点K， K 即是C点到AB的垂足。再求出CK 的实长。
c
X
b b
c
a
37
垂直问题
作图过程
a
1
k
d
c 实长
2
X
b
21

● ●
⑵ 直线为特殊位置
b m
k
a
●
●
n
1(2)
c
b
k● 2 m(n) ● 1
●
a
c
空间及投影分析 直线MN为铅垂线，其 水平投影积聚成一个点， 故交点K的水平投影也积聚 在该点上。 作图 用面上取点法 ① 求交点 ② 判别可见性 点Ⅰ位于平面上，在前； 点Ⅱ位于MN上，在后。故 k 2为不可见。
a f
c
① 求交线 ② 判别可见性 点Ⅰ在FH上，点Ⅱ在BC上， 点Ⅰ在上，点Ⅱ在下，故fh可 见，n2不可见。
•
V
直线与特殊位置平面相交
b
N n
a
P m
k
B
K a b k M c n k
A PH a
c
C H
m
b
c
由于特殊位置平面的某些投影有积聚性，交点可直接求出。
•
V
判断直线的可见性
a
P m
b
n
N
k
B
K
A PH M a
c a n k b
b k c
C H
m
c
特殊位置线面相交，根据平面的积聚性投影，能直接判别直线的可见性。
第三节 直线、平面与平面的相对位置
相对位置包括平行、相交和垂直。 一、平行问题
包 括
⒈ 直线与平面平行
直线与平面平行 平面与平面平行
定理：
若一直线平行于平面上的某一直 线，则该直线与此平面必相互平行。
例1：过M点作直线MN平行于平面△ABC。
b
有无数解
n
c m
●
a
b
n a
●
c

工程制图直线与平面平面与平面的 相对位置
直线与平面、平面与平面得相对位置 相对位置包括平行、相交与垂直。
一、直线与平面平行
若平面外的一直线与平面内的一 条直线平行，则该直线与此平面平行。
利用该定理:① 在平面外作一直线与平面平行 ② 判断平面外直线与平面就是否平行
例1:过M点作直线MN平行于平面ABC。
p m
c
A
判别
可见性
a
n b
a
P
M
C
N
B m
a
m
n
pH b
作图过程
pHn b
c H
空间及投影分析
c
ABC就是一般位置平面, 平
面P就是铅垂面,其水平投影积聚成
直线 pH ,pH与abc得交点m、n 即 为两平面交线MN得水平性投影。
例2:求矩形平面P与ABC得交线MN,并判别可见性。
p b m
a n
有多少解？ a
a
b c m
●
b
●
mc
n
有无数解
n
例2:过M点作一正平线MN平行于平面 ABC。
b
a a
b
cm n ●
c
m●
n
唯一解
例 3
不平行
二、直线与平面相交
直线与平面相交,其交点就是直线与平 面得共有点。
要讨论得问题: ● 求直线与平面得交点。
● 判别两者之间得相互遮挡关系,即判别可 见性。 我们先讨论直线或平面中至少有一个 处于特殊位置得情况。
⒉ 两平面平行 必须就是一个平面上得一对相交直线对应平行
于另一个平面上得一对相交直线。
1、平面为特殊位置
例:求直线MN与平面ABC得交点K,并判别可见性。

分析：线线//，则线面//；过A点做直线AD//BC。
f’
f
可过A点任意作直线AF
例2：过M点作直线MN平行于平面ABC。
n
a
c
b
m
a
b
c
m
n
有无数解
分析:过M点作一条//平面内的任意直线的直线,即得.
正平线
c
●
b
a
m
a
b
c
m
n
唯一解
n
分析:在平面ABC内作一条正平线,MN//此正平线,即得.
例3：过M点作直线MN平行于V面和平面ABC。
2.另两个投影面上的投影有类似性。
γ
β
是什么位置的平面？
投影特征：一斜两类似
2） 投影面平行面的投影
V
W
H
水平面
投影特性： 1.abc//OX、 abc//OYW，分别积聚为直线; 2 .水平投影abc反映 ABC实形。
C
A
B
a
b
c
b
a
c
a
b
c
c
a
b
b
b
a
a
椭圆的画法
一节到此
椭圆的近似画法(四心法)：
A
B
C
D
E
F
1
2
3
4
1.CF=CE=OA-OC
O
2.作AF的中垂线,与两轴交得1.2两点，取对称点3.4。
3.分别以1.2.3.4点为圆心，1为半径作弧，拼成近似椭圆。
四、相互垂直的两直线的投影特性
⒈ 两直线同时平行于某一投影面时，在该投影面上的投影反映直角。
⒈ 直线与平面平行

21:14:50 8
Y a
§2.6 平面的投影-各类平面的投影特性－投影面平行面－水平面 Z a' A X b' c' B a b" a" C c" b' c Z
b" a"
c"
X
a
b a
c Y
b
YV
YH 投影特性： (1) abc、 abc重影为一条线，具有积聚性 (2) 水平投影 abc反映 ABC实形
21:14:50 6
§2.6 平面的投影-各类平面的投影特性－投影面垂直面－正垂面 b QV a c X C A B Z a' b' Z b"
a"
c"
c'
X
Q c
Y
a
YV
投影特性 b YH (1) abc重影为一条线 (2) abc、 abc为 ABC的类似形 (3) abc与OX、OZ的夹角反映α、 的真实大小
工程制图
Engineering Drawing
十五国家重点图书
第2章 平面
§2.6 平面的投影
§2.7 平面上的点和直线
§2.8 直线、平面与平面的相对位置
§2.6 平面的投影-平面的投影图 c c a a b
c b b b a a b a a c b b
b
a a c a d b b d
e
1 k
m d
c
a b
2
X
c
b k
1(2)
e m d
a
特殊位置直线与一般位置平面
21:14:50 28
§2.8直线、平面与平面间的相对位置-相交－重影性法-例子 [例2]求直线AB与铅垂面EFGH的交点K。 e h a

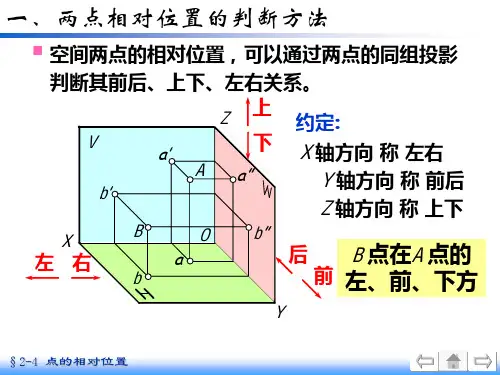
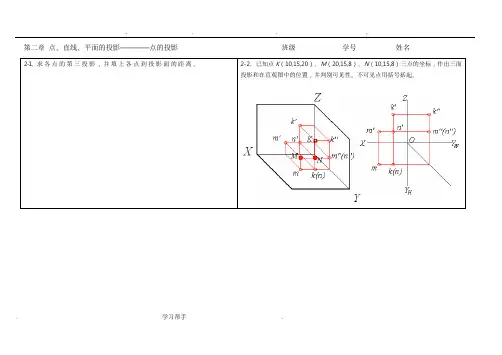
2-1、求各点的第三投影，并填上各点到投影面的距离。

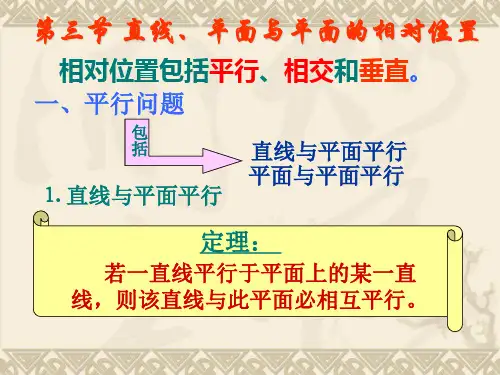
2-2、已知点K（10,15,20）、M（20,15,8）、N（10,15,8）三点的坐标，作出三面投影和在直观图中的位置，并判别可见性。

不可见点用括号括起。

精选文档A点距V面（5 ）、距H面（6）、距W面（8 ）B点距V面（ 4 ）、距H面（ 3 ）、距W面（ 2 ）C点距V面（ 2 ）、距H面（ 2 ）、距W面（2）D点距V面（0）、距H面（ 3 ）、距W面（ 6 ）E点距V面（ 2 ）、距H面（0 ）、距W面（ 3 ）F点距V面（6 ）、距H面（5 ）、距W面（0 ）2-3、比较A、B、C三点的相对位置。

（下）mmB点在A点（左）mm（前）mm（上）mmB点在C点（左）mm（后）mm（下）mmC点在A点（右）mm（前）mm第二章点、直线、平面的投影————点的投影班级学号姓名精选文档2-4 已知E（22，30，20），F点在E点之左10mm，之下10mm，之后10mm；G点在E点的正右方12mm，作出点E 、F 、G的三面投影。

2-5已知A（24，18，20），B点（24，18，0），以及点C在点A之右10mm，之上16mm，之前12mm，作出点A 、B 、C的三面投影。

2-6 作出点D（30，0，20）、点E（0，0，20），以及点F在点D的正前方25mm，作出这三个点的三面投影。

13第二章点、直线、平面的投影————点的投影班级学号姓名精选文档2-7已知物体的立体图和投影图，试把A、B、C、D、E各点标注到投影图上的对应位置，并把重影点处不可见点加上括号。

2-8已知A、B两点是一对V面重影点，相距10mm；A、C两点是一对H面的重影点，C 在H面上；D点在H面上，且在C后15mm，右15mm，求B、C、D三点的三面投影，并判别重影点的可见性。

OXZY HY Wa′(b′)bc′(c)dd′a″ad″c″b″14第二章点、直线、平面的投影————直线的投影班级学号姓名精选文档15第二章点、直线、平面的投影————直线的投影班级学号姓名精选文档第二章点、直线、平面的投影———直线的实长班级学号姓名精选文档精选文档第二章点、直线、平面的投影———直线的实长班级学号姓名精选文档18第二章点、直线、平面的投影———直线上的点班级学号姓名精选文档第二章点、直线、平面的投影———两直线的相对位置班级学号姓名精选文档2-23判别AB和CD两直线的相对位置（平行、相交、交叉）。

例2：判别直线AB 是否 平行于平面DEF。
b c m b a c m
n
a
b
e
a
d
g
f
n
a b e 结论：直线AB不平行于定平面 d g f
方法：作MN平行于AB。
例3：试过点D作水平线DE平行于ΔABC平面
b d e a f c
e d
c
f
c a
２.两平面平行
条件： 若一平面上的两相交直线对应平行于另一平面上的 两相交直线，则这两平面相互平行。 Q D
§2-5
直线与平面及两平面的相对位置
2.5.1 直线与平面及两平面平行
2.5.2 直线与平面及两平面相交 2.5.3 直线与平面及两平面垂直
2. 5. 1 直线与平面及两平面平行
１.直线与平面平行
P m
条件:
若一直线平行于平面上
A
的某一直线，则该直线与此
平面平行。
n
B
例1：过M点作直线MN 平行于平面ABC。
f ef k b
1
2
a
k
(二) 一般位置平面与特殊位置平面相交
——求交线并判别可见性 m
M B K P
b
f n k l
c
a
a l
A L
F N m C f b n k a l
m
k b
f
c
n
c PH
将一般位置平面视为两相交直线，分别求一般位置直线与特殊位置 平面的交点，交点相连即为交线
例2：求两特殊位置平面的交线并判断可见性。
e
c
A B C ab cd ef
E D F H G b a d c e

画法几何及工程制图2§3.2 点的二面投影（two-plane projection of point）一、二面投影体系的建立及点的二面投影点是形体最基本的元素。

在几何学中无大小、薄厚、宽窄，只占有位置。

空间点用大写字母表示，投影点用小写字母表示。

图 2设立一个投影面P，则A1、 A2、A3点在投影面P上的正投影是唯一的。

但反过来，若知道了点的一个投影，却不能确定点的空间位置（缺少一个坐标）。

因此要确定一个点的空间位置，只有一个投影是不够的。

现设立两个互相垂直的投影面正立投影面V（也称正面或V面）、水平投影面H（也称水平面或H面），从而构成二投影面体系。

V面和H面的交线OX称为投影轴。

A点的在V面上的投影称为A点的正面投影或A点的正投影、A 点的V投影，用a’表示。

A点的在H面上的投影称为A点的水平投影或A点的H投影，用a表示。

图 3我们需要把这种空间关系在一种图纸上（一个平面上）表达出来。

保持V面不动，H面绕OX轴向下旋转90o直至与V面重合，从而得到点的二面投影图。

为简便起见，投影图中投影面的边框不必画出。

在点的二面投影体系中，X、Y、Z三个坐标均能体现，故点的二面投影就唯一确立了点在空间的相对位置（相对二面投影体系）。

图4容易得出点在二面投影体系中的投影规律：⒈点的两投影的连线⊥投影轴。

证明。

⒉投影点到投影轴的距离，反映该空间点到另一投影面的距离。

二、点在四个象角中的投影平面本身是可以无限延长的，因此就有上V面、下V面、前H面和后H面，它们把空间分为四个部分──四个象限或象角。

分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ标记。

画投影图时仍然保持V面不动，前H面向下旋转与下V重合，后H面向上旋转与上V重合，只画OX轴，不必注投影面标记，也不用画边框。

⒈在四个象角内的点。

（1）A点在Ⅰ象角内。

其正面投影a’在OX轴上方，水平投影a在OX轴下方。

（2）B点在Ⅱ象角内。

H面之上，V面之后。

正投影b’在OX 轴上方，水平投影b也在OX轴上方。