北京市海淀外国语实验学校2020-2021学年第一学期 12月月练习八年级数学试题

2020-2021学年北京市海淀区八年级上期中数学试卷
一、选择题（每题3分，共30分，每题只有一个正确选项，请填写在后边给出的括号内）. 1．（3分）下列四个图形中，不是轴对称图形的是（）
A．B．
C．D．
2．（3分）点P（3，﹣5）关于x轴对称的点的坐标为（）
A．（﹣3，﹣5）B．（5，3）C．（﹣3，5）D．（3，5）
3．（3分）如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（）
A．∠A＝∠C B．∠D＝∠B C．AD∥BC D．DF∥BE
4．（3分）下列计算中正确的是（）
A．2x+3y＝5xy B．x•x4＝x4
C．（x2y）3＝x6y3 D．x8﹣x2＝x6
5．（3分）若一个正多边形的每一个内角为156°，则这个正多边形的边数是（）A．14B．15C．16D．17
6．（3分）如果等腰三角形的两边长是10cm和5cm，那么它的周长为（）A．20cm B．25cm C．20cm或25cm D．15cm
7．（3分）AD是△ABC的角平分线，作DE⊥AB于E，DF⊥AC于F，下列结论错误的是（）
A．BD＝CD B．AE＝AF C．DE＝DF D．∠ADE＝∠ADF 8．（3分）如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（）
第1 页共18 页。

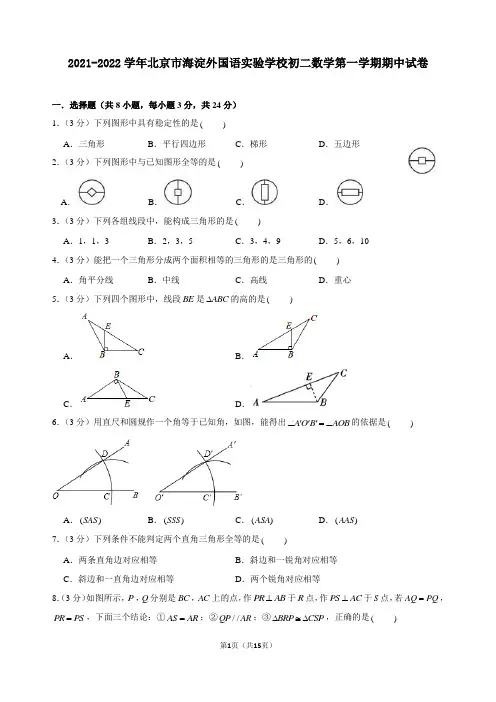
2021-2022学年北京市海淀外国语实验学校初二数学第一学期期中试卷一．选择题（共8小题，每小题3分，共24分）1．（3分）下列图形中具有稳定性的是( )A ．三角形B ．平行四边形C ．梯形D ．五边形2．（3分）下列图形中与已知图形全等的是( )A ．B ．C ．D ．3．（3分）下列各组线段中，能构成三角形的是( )A ．1，1，3B ．2，3，5C ．3，4，9D ．5，6，104．（3分）能把一个三角形分成两个面积相等的三角形的是三角形的( )A ．角平分线B ．中线C ．高线D ．重心5．（3分）下列四个图形中，线段BE 是ABC ∆的高的是( )A ．B ．C ．D ．6．（3分）用直尺和圆规作一个角等于已知角，如图，能得出AO B AOB ∠'''=∠的依据是( )A ．()SASB ．()SSSC ．()ASAD ．()AAS7．（3分）下列条件不能判定两个直角三角形全等的是( )A ．两条直角边对应相等B ．斜边和一锐角对应相等C ．斜边和一直角边对应相等D ．两个锐角对应相等 8．（3分）如图所示，P ，Q 分别是BC ，AC 上的点，作PR AB ⊥于R 点，作PS AC ⊥于S 点，若AQ PQ =，PR PS =，下面三个结论：①AS AR =；②//QP AR ；③BRP CSP ∆≅∆，正确的是( )A ．①和③B ．②和③C ．①和②D ．①，②和③二、填空题（共8小题.每小题3分，共24分）9．（3分）如图，已知AD AE =，请你添加一个条件，使得ADC AEB ∆≅∆，你添加的条件是 ．（不添加任何字母和辅助线）10．（3分）已知直角三角形的一个锐角的度数为37︒，则其另一个锐角的度数为 度．11．（3分）一个多边形的内角和跟它的外角和相等，则这个多边形是 边形．12．（3分）如图是由6个边长相等的正方形组合成的图形，123∠+∠+∠= ．13．（3分）如图，ABC ∆中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，垂足为E ，10AB =，6AC =，则BE 的长为 ．14．（3分）在ABC ∆中，已知6AB =，5AC =，AD 是BC 边上的中线，则AD 取值范围是 ．15．（3分）如图，AOD BOC ∆≅∆，50C ∠=︒，40COD ∠=︒，AD 与BC 相交于点E ，则DEC ∠= ︒．16．（3分）当三角形中一个内角β是另外一个内角α的12时，我们称此三角形为“友好三角形”，α为友好角．如果一个“友好三角形”中有一个内角为54︒，那么这个“友好三角形”的“友好角α”的度数为．三、解答题（共6小题，17、18每小题4分，19、20、21、22每小题4分，共32分）17．（4分）求出下列图形中x的值．18．（4分）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．（1）利用尺规作图在AC边上找一点D，使点D到AB、BC的距离相等．（不写作法，保留作图痕迹）（2）在网格中，ABC∆的下方，直接画出EBC∆，使EBC∆与ABC∆全等．19．（6分）看对话答题：小梅说：这个多边形的内角和等于1125︒．小红说：不对，你少加了一个角．问题：（1）他们在求几边形的内角和？（2）少加的那个内角是多少度？20．（6分）已知：如图，CB CD=，分别过点B和点D作AB BC⊥，AD DC⊥，两垂线相交于点A．求证：AB AD=．21．（6分）如图，A，E，C三点在同一直线上，且ABC DAE∆≅∆．（1）线段DE，CE，BC有怎样的数量关系？请说明理由．（2）请你猜想ADE∆满足什么条件时，//DE BC，并证明．22．（6分）如图，大小不同的两块三角板ABC=，DC EC=，∆直角顶点重合在点C处，AC BC∆和DEC连接AE、BD，点A恰好在线段BD上．（1）找出图中的全等三角形，并说明理由；（2）当4AD AB cm==，则AE的长度为cm．（3）猜想AE与BD的位置关系，并说明理由．四．能力展示题（共3小题，第23、24每小题6分，25题8分，共20分）23．（6分）在ABC∆中，70∠=︒．A（1）如图1，ABC∠=︒；∠、ACB∠的平分线相交于点O，则BOC（2）如图2，ABC∠的平分线相交于点O'，则BO C'∠=︒；∠、BCE∆的外角CBD（3）探究如图3，ABC∠的平分线相交于点O，设A n∠=︒，则∠的平分线与其外角ACD∆的内角ABC∠的度数是．（用n的代数式表示）BOC24．（6分）若三边均不相等的三角形三边a 、b 、c 满足(a b b c a ->-为最长边，c 为最短边），则称它为“不均衡三角形”．例如，一个三角形三边分别为7，5，4，因为7554->-，所以这个三角形为“不均衡三角形”．（1）以下4组长度的小木棍能组成“不均衡三角形”的为 （填序号）．①4cm ，2cm ，1cm ；②13cm ，18cm ，9cm ；③19cm ，20cm ，19cm ；④9cm ，8cm ，6cm ．（2）已知“不均衡三角形”三边分别为22x +，16，26x -，直接写出x 的整数值为 ．25．（8分）数学课上，老师给出了如下问题：已知：如图1，在Rt ABC ∆中，90C ∠=︒，AC BC =，延长CB 到点D ，45DBE ∠=︒，点F 是边BC 上一点，连接AF ，作FE AF ⊥，交BE 于点E ．（1）求证：CAF DFE ∠=∠；（2）求证：AF EF =．经过独立思考后，老师让同学们小组交流．小辉同学说出了对于第二问的想法：“我想通过构造含有边AF 和EF 的全等三角形，因此我过点E 作EG CD ⊥于G （如图2所示），如果能证明Rt ACF ∆和Rt FGE ∆全等，问题就解决了．但是这两个三角形证不出来相等的边，好像这样作辅助线行不通．”小亮同学说：“既然这样作辅助线证不出来，再考虑有没有其他添加辅助线的方法．”请你顺着小亮同学的思路在图3中继续尝试，并完成（1）、（2）问的证明．参考答案与试题解析一．选择题（共8小题，每小题3分，共24分）1．【解答】解：A．三角形具有稳定性，故本选项符合题意；B．平行四边形不具有稳定性，故本选项不符合题意；C．梯形不具有稳定性，故本选项不符合题意；D．五边形不具有稳定性，故本选项不符合题意；故选：A．2．【解答】解：A、圆里面的正方形与已知图形不能重合，错；B、与已知图形能完全重合，正确；C、中间是长方形，与已知图形不重合，错；D、中间是长方形，与已知图形不重合，错．故选：B．3．【解答】解：A、1123+=<，∴无法构成三角形，不合题意；B、235+=，∴无法构成三角形，不合题意；+=<，C、3479∴无法构成三角形，不合题意；D、561110+=>，∴可以构成三角形，符合题意；故选：D．4．【解答】解：能把一个三角形分成两个面积相等的三角形的是三角形的中线．故选：B．5．【解答】解：线段BE是ABC∆的高的图是选项D．故选：D．6．【解答】解：作图的步骤：①以O为圆心，任意长为半径画弧，分别交OA、OB于点D、C；②任意作一点O'，作射线O B''，以O'为圆心，OC长为半径画弧，交O B''于点C'；③以C'为圆心，CD长为半径画弧，交前弧于点D'；④过点D '作射线O A ''．所以AO B ∠'''就是与AOB ∠相等的角；作图完毕．在OCD ∆与△O C D '''，OC O C OD O D CD C D =''⎧⎪=''⎨⎪=''⎩，OCD ∴∆≅△()O C D SSS '''，AO B AOB ∴∠'''=∠，显然运用的判定方法是SSS ．故选：B ．7．【解答】解：A 、根据SAS 定理可知，两条直角边对应相等的两个三角形全等，本选项不符合题意； B 、根据AAS 定理可知，斜边和一锐角对应相等的两个三角形全等，本选项不符合题意； C 、根据HL 定理可知，斜边和一直角边对应相等的两个三角形全等，本选项不符合题意； D 、两个锐角对应相等的两个三角形不一定全等，本选项符合题意；故选：D ．8．【解答】解：连接AP ，PR PS =，AP ∴是BAC ∠的平分线，()APR APS HL ∴∆≅∆AS AR ∴=，①正确．AQ PQ =BAP QAP QPA ∴∠=∠=∠//QP AR ∴，②正确．BC 只是过点P ，并没有固定，明显BRP CSP ∆≅∆③不成立．故选：C ．二、填空题（共8小题.每小题3分，共24分）9．【解答】解：A A ∠=∠，AD AE =，∴可以添加AB AC =，此时满足SAS ；添加条件ADC AEB ∠=∠，此时满足ASA ；添加条件ABE ACD ∠=∠，此时满足AAS ，故答案为AB AC =或ADC AEB ∠=∠或ABE ACD ∠=∠；10．【解答】解：直角三角形的一个锐角的度数为37︒，∴其另一个锐角的度数903753=︒-︒=︒，故答案为：53．11．【解答】解：设多边形的边数为n ，根据题意(2)180360n -⋅︒=︒，解得4n =．故答案为：4．12．【解答】解：如图，根据题意得DE BC =，EC AB =，GF GC =，90DEC ABC FGC ∠=∠=∠=︒， CGF ∴∆为等腰直角三角形，245∴∠=︒，在ABC ∆和CED ∆中，AB CE ABC CED BC ED =⎧⎪∠=∠⎨⎪=⎩，()ABC CED SAS ∴∆≅∆，1DCE ∴∠=∠，390DCE ∠+∠=︒，1390∴∠+∠=︒，1239045135∴∠+∠+∠=︒+︒=︒．故答案为135︒．13．【解答】解：AD 是CAB ∠的平分线，EAD CAD ∴∠=∠，DE AB ⊥，90DEA C ∴∠=∠=︒，在ADE ∆和ADC ∆中，DEA DCA EAD CAD AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADE ADC AAS ∴∆≅∆，6AE AC ∴==，1064BE AB AE ∴=-=-=，故答案为4．14．【解答】解：延长AD 到E 使DE AD =，连接BE ，如图， AD 是BC 边上的中线，BD CD ∴=，在BDE ∆和CDA ∆中，BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩，()BDE CDA SAS ∴∆≅∆，5BE AC ∴==，AB BE AE AB BE -<∠+，即65265AD -<<+， ∴11122AD <<． 故答案为11122AD <<．15．【解答】解：设DO 交BC 于F ，AOD BOC ∆≅∆，50C ∠=︒，D C ∴∠=∠，180D DEC DFE ∠+∠+∠=︒，180C DOC OFC ∠+∠+∠=︒，又DFE OFC ∠=∠，DEC COD ∴∠=∠，40COD ∠=︒，40DEC ∴∠=︒，故答案为：40．16．【解答】解：①54︒角是α，则友好角度数为54︒；②54︒角是β，则1542αβ==︒， 所以，友好角108α=︒；③54︒角既不是α也不是β，则54180αβ++︒=︒， 所以，1541802αα++︒=︒， 解得84α=︒，综上所述，友好角度数为54︒或84︒或108︒．故答案为：54︒或84︒或108︒．三、解答题（共6小题，17、18每小题4分，19、20、21、22每小题4分，共32分）17．【解答】解：（1）180?90?5040x =︒︒︒=︒；（2）40180x x ++=︒，70x ∴=；（3）7010x x x +=++，解得60x =．18．【解答】解：（1）如图点D 即为所求；（2）EBC ∆或△E BC '即为所求；19．【解答】解：（1）设少加这个内角为x ︒，这个多边形的边数为n 则1125(2)180x n +=-，(2)1801125x n =--，0180x <<，0(2)1801125180n ∴<--<， n 为整数，9n ∴=．（2）(92)1801125135x =-⨯-=，∴少加这个内角为135度．20．【解答】证明：连接AC ，AB BC ⊥，AD CD ⊥90B D ∴∠=∠=︒，在Rt ABC ∆和Rt ADC ∆中AC AC BC DC =⎧⎨=⎩Rt ABC Rt ADC(HL)∴∆≅∆AB AD ∴=21．【解答】（1）解：DE CE BC =+．理由：ABC DAE ∆≅∆，AE BC ∴=，DE AC =． A ，E ，C 三点在同一直线上，AC AE CE ∴=+，DE CE BC ∴=+；（2）当ADE ∆满足90AED ∠=︒时，//DE BC ，证明：ABC DAE ∆≅∆，90AED ∠=︒，90C AED ∴∠=∠=︒，18090DEC AED ∠=︒-∠=︒，C DEC ∴∠=∠．//DE BC ∴，即当ADE ∆满足90AED ∠=︒时，//DE BC ．22．【解答】解：（1）CBD CAE ∆≅∆，理由如下：90ACB DCE ∠=∠=︒，ACB ACD DCE ACD ∴∠+∠=∠+∠，即BCD ACE ∠=∠，在CBD ∆与CAE ∆中，BC AC BCD ACE DC EC =⎧⎪∠=∠⎨⎪=⎩，()CBD CAE SAS ∴∆≅∆；（2）CBD CAE ∆≅∆，448()BD AE AD AB cm ∴==+=+=，故答案为：8；（3）AE BD ⊥，理由如下：AE 与CD 相交于点O ，在AOD ∆与COE ∆中，CBD CAE ∆≅∆，ADO CEO ∴∠=∠，AOD COE ∠=∠，90OAD OCE ∴∠=∠=︒，AE BD ∴⊥．四．能力展示题（共3小题，第23、24每小题6分，25题8分，共20分）23．【解答】解：（1）70A ∠=︒，180110ABC ACB A ∴∠+∠=︒-∠=︒． BO 平分ABC ∠，CO 平分ACB ∠，12OBC ABC ∴∠=∠，12OCB ACB ∠=∠． 111()55222OBC OCB ABC ACB ABC ACB ∴∠+∠=∠+∠=∠+∠=︒． 180()125BOC OBC OCB ∴∠=︒-∠+∠=︒．故答案为：125︒．（2）DBC A ACB ∠=∠+∠，BCE A ABC ∠=∠+∠，18070250DBC BCE A ACB A ABC ∴∠+∠=∠+∠+∠+∠=︒+︒=︒． BO '平分DBC ∠，CO '平分BCE ∠，12O BC DBC ∴∠'=∠，12O CB ECB ∠'=∠． 111()125222O BC O CB DBC ECB DBC ECB ∴∠'+∠'=∠+∠=∠+∠=︒． 180()18012555BO C O BC O CB ∠'=︒-∠'+∠'=︒-︒=︒．故答案为：55︒．（3）BO 平分ABC ∠，CO 平分ACE ∠，2ABC OBC ∴∠=∠，2ACE OCE ∠=∠．A ACE ABC ∠=∠-∠，222()2A OCE OBC OCE OBC BOC ∴∠=∠-∠=∠-∠=∠．1122BOC A n ∴∠=∠=︒． 故答案为：12n ︒． 24．【解答】解：（1）①124+<，4cm ∴，2cm ，1cm 不能组成“不均衡三角形”； ②1813139->-，13cm ∴，18cm ，9cm 能组成“不均衡三角形”； ③1919=，19cm ∴，20cm ，19cm 不能组成“不均衡三角形”； ④9886-<-，9cm ∴，8cm ，6cm 不能组成“不均衡三角形”． 故答案为：②；（2）①16(22)22(26)x x x -+>+--，解得3x <，260x ->，解得3x >，故不合题意舍去；②221626x x +>>-，解得711x <<，221616(26)x x +->--，解得9x >，911x ∴<<， x 为整数，10x ∴=，经检验，当10x =时，22，16，14可构成三角形； ③2616x ->，解得11x >，22(26)2616x x x +-->--，解得15x <，1115∴<<，xx为整数，x∴=或13或14，都可以构成三角形．12综上所述，x的整数值为10或12或13或14．故答案为：10或12或13或14．25．【解答】证明：（1）90C∠=︒，∴∠+∠=︒．CAF AFC90⊥，FE AF∴∠+∠=︒．90DFE AFC∴∠=∠．CAF DFE（2）如图3，在AC上截取AG BF=，连接FG，=，AC BC=．AC AG BC BF∴-=-，即CG CF∠=︒，C90∴∠=∠=︒．CGF CFG45∴∠=︒-∠=︒．AGF CGF180135DBE∠=︒，45∴∠=︒-∠=︒．FBE DBE180135∴∠=∠．AGF FBE由（1）可得：CAF DFE∠=∠．∴∆≅∆．AGF FBE ASA()∴=．AF EF。

2020-2021学年北京市海淀区北京一零一中学八上期中数学模拟试卷一、选择题（共10小题；共40分）1. 下列平面图形中，不是轴对称图形的是A. B.C. D.2. 下列运算正确的是A. B. C. D.3. 如果等腰三角形的一个内角等于，则它的底角是A. B. C. D. 或4. 已知：，，则A. B. C. D.5. 如图，在中，，，下列结论不一定正确的是A. B.C. 平分D.6. 如图，，且，则度数为A. B. C. D.7. 如图，在的两边上分别取点，使得，将两个全等的直角三角板的直角顶点分别放在点，处，一条直角边分别落在的两边上，另一条直角边交于点，连接，则判定的依据是A. B. C. D.8. 点关于轴的对称点是A.9. 如图，为边上一点，，且，，则等于A. B. C. D.10. 如图，等腰中，，于．的平分线分别交，于点，两点，为的中点，延长交于点，连接．下列结论：① ；② ；③ 是等腰三角形；④ ．其中正确的结论个数是A. 个B. 个C. 个D. 个二、填空题（共10小题；共40分）11. 若，则．12. 已知等腰三角形的两边分别是和，则该等腰三角形的周长为．13. 如图，点，，，在同一条直线上，欲证，已知，，还可以添加的条件是．14. 将边长分别为和的两个正方形按如图的形式摆放，求图中阴影部分的面积．15. 如图，等边中，，分别是，边上的一点，且，则．16. 如图，在中，，，平分交于点，于点．若，则的周长为．17. 已知，则．18. 如图，已知三角形纸片，，，将其折叠，如图，使点与点重合，折痕为，点，分别在，上，求的大小．．19. 中，．设的面积为．①图中，为中点，，，，是上的四点；②图中，，，，，，，交于点；③图中，，为中点，．其中，阴影部分面积为的是（填序号）．20. 如图，在长方形的对称轴上找点，使得，均为等腰三角形，则满足条件的点有个．三、解答题（共8小题；共73分）21. 计算下列各题．（1）；（2）求的值，其中．22. 解方程或不等式．（1）；（2）．23. 如图，是线段的中点，，，求证：．24. 作图题：国庆节期间小红外出游玩时看到了映山红拼成的“”字样，还有两个花坛，，请帮小红找一处最佳观赏位置，满足观赏点到“”字样的两边距离都相等，并且到两个花坛，的距离也都相等（尺规作图，保留作图痕迹并写出结论）．结论为：．25. 已知：在中，，，分别是线段，上的一点，且．（1）如图，若，是中点，则的度数为．（2）借助图探究并直接写出和的数量关系．26. 在中，，，平分交于，，在，上，且．（1）求的度数；（2）求证：．27. 我们曾学过定理“在直角三角形中，如果一个锐角等于，那么它所对的直角边等于斜边的一半”，其逆命题也是成立的，即“在直角三角形中，如果一直角边等于斜边的一半，那么该直角边所对的角为”．如图，在中，，如果，那么．请你根据上述命题，解决下面的问题：（1）如图，，为格点，以为圆心，长为半径画弧交直线于点，则；（2）如图，，为格点，按要求在网格中作图（保留作图痕迹）．作，使点在直线上，并且，．（3）如图，在中，，，为内一点，，于，且．①求的度数；②求证：．28. 如图，是等边三角形的边所在直线上一点，是边所在直线上一点，且与不重合，若，则称为点关于等边三角形的反称点，点称为反称中心．在平面直角坐标系中．（1）已知等边三角形的顶点的坐标为，点在第一象限内，反称中心在直线上，反称点在直线上．①如图，若为边的中点，在图中作出点关于等边三角形的反称点，并直接写出点的坐标：；②若，求点关于等边三角形的反称点的坐标；（2）若等边三角形的顶点为，，反称中心在直线上，反称点在直线上，且．请直接写出点关于等边三角形的反称点的横坐标的取值范围：（用含的代数式表示）．答案第一部分1. A2. B 【解析】与不是同类项，所以不能合并，故选项A不合题意；，故选项B符合题意；，故选项C不合题意；，故选项D不合题意．3. A 【解析】等腰三角形的一个内角等于，等腰三角形的顶角为，等腰三角形的底角为．4. B 【解析】，．5. D【解析】在中，，为等腰三角形，，，，平分，不能得到，则无法证明．6. C 【解析】，，，即．7. D 【解析】，在与中，．8. A 【解析】根据“关于轴对称的点，横坐标相同，纵坐标互为相反数”，可知：点关于轴的对称点为．9. A 【解析】，，在和中，，，，则．10. D【解析】，，，，，，，平分，，，，，为的中点，，，，在和中．，，①正确；在和中，，，，，②正确；，，，四点共圆，，，④正确；，，，是等腰三角形，③正确．即正确的有个．第二部分11.【解析】．12.【解析】当为底时，其它两边都为，，，可以构成三角形，周长为；当为腰时，其它两边为和，因为，所以不能构成三角形，故舍去．13. （答案不唯一）【解析】还可以添加的条件是：，在与中．．【解析】由图可得阴影部分的面积等于两个正方形的面积的和减去一个直角三角形的面积．由图可得阴影部分的面积．15.【解析】为等边三角形，，．在和中，，．，，．16.【解析】平分交于，于，，，，，，，【解析】，，．，，．【解析】，，而，，使点与点重合，折痕为，，．19. ①②③【解析】如图，，点是中点，，垂直平分，，，，，，阴影部分面积为；如图，，，是等边三角形，且，，，垂直平分，垂直平分，垂直平分，，，，阴影部分面积为；如图，连接，，，为中点，，，，，且，，且，，．，阴影部分面积为．20.【解析】如图，作或的垂直平分线交于，如图，在上作点，使，同理，在上作点，使，如图，在长方形外上作点，使，同理，在长方形外上作点，使，故答案为．第三部分21. （1）．（2）当时，22. （1）（2）23. 是的中点，．在和中，．24. 如图，点即为所求25. （1）【解析】，，，，，，是中点，，，即，．（2）【解析】，，，，，，，即，．26. （1），，，平分，，．（2）由（）得：，，，，，，在和中，，，，．27. （1）【解析】如图中，作于．由作图可知：，．（2）如图即为所求．（3）① 于，且，．②作于．，，，，，，，，，，，，．28. （1）；② 等边三角形的两个顶点为，，．．是等边三角形的边所在直线上一点，且，点与坐标原点重合或点在边的延长线上，如图，若点与坐标原点重合，，，．是边所在直线上一点，且与不重合，点坐标为．如图，若点在边的延长线上，且，，．为等边三角形，．．．，点与点重合．这与题目条件中的与不重合矛盾，故这种情况不合题意，舍去．综上所述：．【解析】①如图，过点作，垂足为．，，，点的坐标为，，点是的中点，，，，，，，，，，点坐标．（2）或【解析】，，，．，点在的延长线上或在的延长线上，如图点在的延长线上，过点作，过点作．，，，，，．，若，，，，，，的横坐标为；若，，，，，，的横坐标为，点的横坐标的取值范围：，如图点在的延长线上，过点作，过点作，同理可求：点的横坐标的取值范围：．综上所述：点的横坐标的取值范围：或．。

2020-2021学年北京市海淀区北京一零一中学八上期中数学模拟试卷
一、选择题（共10小题；共40分）
1. 下列平面图形中，不是轴对称图形的是
A. B.
C. D.
2. 下列运算正确的是
A. B. C. D.
3. 如果等腰三角形的一个内角等于，则它的底角是
A. B. C. D. 或
4. 已知：，，则
A. B. C. D.
5. 如图，在中，，，下列结论不一定正确的是
A. B.
C. 平分
D.
6. 如图，，且，则度数为
A. B. C. D.
7. 如图，在的两边上分别取点，使得，将两个全等的直角三
角板的直角顶点分别放在点，处，一条直角边分别落在的两边上，另一条直角边交于点，连接，则判定的依据是
A. B. C. D.
8. 点关于轴的对称点是
A.
9. 如图，为边上一点，，且，，则
等于
A. B. C. D.
10. 如图，等腰中，，于．的平分线分
别交，于点，两点，为的中点，延长交于点，连接．下列结论：
① ；
② ；
③ 是等腰三角形；
④ ．
其中正确的结论个数是。

21EFACDABCDEF北京市海淀区2020—2021学年度八年级第一学期期中测试卷科 目：数学总分： 100 时间：90 分钟一、选择题：把正确的选项填在表格中相应的题号下（每小题3分，共24分） 题号 12345678答案1．在下图中，是轴对称图形．．．．．的是 （ ）2．下列运算结果正确的是（ ）A ． 3412a a a ⋅=B ．()236aa -= C ．235ab ab += D ．()236ab ab =3．点M （1，2）关于y 轴对称的点的坐标为（ ）A ．（－1，－2）B ．（－1，2）C ．（2，－1）D ．（1，－2） 4. 小芳画一个有两边长分别为5和6的等腰三角形，则它的周长是（ ）A ．16B ．17C ．11D ．16或17 5．适合条件∠A =∠B =2∠C 的△ABC 是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定6．如图，已知AB =D E ，∠1=∠2，要得到△ABC ≌△DEF ，还应给出的条件是（ ） A ．∠B =∠E B ．BC =ED C ．AB =EF D ．CD = AF第6题图 第7题图 第8题图第13图7. 如图，AD 是△ABC 的角平分线,从点D 向AB 、AC 两边作垂线段，垂足分别为E 、F ，那么下列结论中错误的是（ ）A ．DE =DF ;B ．AE =AF ;C ．BD =CD ; D ．∠ADE =∠ADF 8．如图：∠EAF =15°，AB =BC =CD =DE =EF ，则∠DEF 等于（ ） A ．90° B ．75° C ．70° D ．60° 二、选择题：（每小题2分，共16分）9．化简：（1）3a a ⋅= ； （2）22312x y ⎛⎫- ⎪⎝⎭= ．10．一个多边形的每个外角都是36°，那么这个多边形的内角和是 度，对角线的条数一共有 条．11. 已知点P （m ，2）与点Q （－4， n ）关于x 轴对称，则m+ n ＝__________.12．如图，△ABC 中，∠C =90°，BD 平分∠ABC 交AC 于点D ，若CD =3，则点D 到AB 的距离为 ．13．如图，在△ABC 中，DE ∥BC ，BD 为∠ABC 的平分线，若AB =10，AD =4，则△AED 的周长等于 ． 14．如图，∠A =90°，∠B=15°，BD =DC ，AC =4，则BD = ．15．如图，DE 是∆ABC 中AC 边的垂直平分线，若∠B =46°，∠BCE =20°，则∠ACE = °． 16．如图，直线l 过正方形ABCD 的顶点B ，点A 、C 到直线l 的距离分别是1和2，则EF 的长是 ． 三、解答题：（共60分） 17.计算： （1）（4分）()()1342+⋅-x x（2）（4分）()()y x y x 2352-+ （3）（4分） ()32126+33aa a a -÷ADBC第14题图CEBDA第15题图 第16题图DC第12题图NMOBA（4）（5分）已知：0432=--xx，求代数式2)3()1)(1(32++--+xxx的值.18．（5分）如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等.你能确定仓库P应该建在什么地方？请用尺规作图确定仓库P的位置.19．（5分）如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴对称的△A1B1C1．20．（5分）已知：如图，AB∥DE，∠A＝∠D，且BE＝CF，求证：AC＝DF．证明：AB CDFF EB DAC21．（5分）如图：在△ABC 中，∠B =90°，AB =BD ，AD =CD ，求∠CAD 的度数． 解：22．（5分）如图，AC ⊥CB , DB ⊥CB , AB =DC ．求证：∠ABD =∠ACD ． 证明：23. （5分）已知：如图：在ΔABC 中AB ＝AC ，D 在BC 的中点，DE ⊥AB 于E ，DF ⊥AC 于F.求证：DE=DF.24.（6分）如图，将两个一大、一小的等腰直角三角尺拼接 （A 、B 、D 三点共线，AB ＝CB ，EB ＝BADCDB，∠ABC＝∠EBD＝90°），连接AE、CD，试确定AE与CD的位置与数量关系，并证明你的结论．25.（7分）已知：如图，RtΔABC中，∠BAC＝90°，AB＝AC，D 是BC的中点，AE＝BF．求证：（1）DE＝DF；（2）ΔDEF为等腰直角三角形．证明：ECB D A选做题：26．（20分）在等边△ABC的两边AB、AC所在直线上分别有两点M、N，D为△ABC外一点，且∠MDN=60°,∠BDC=120°, BD=DC. 探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系．图1 图2 图3（I）如图1，当点M、N边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系Q；是；此时=L（II）如图2，点M、N边AB、AC上，且当DM≠DN时，猜想（I）问的两个结论还成立吗？写出你的猜想并加以证明；（III）如图3，当点M、N分别在边AB、CA的延长线上时，若AN=x，则Q= （用x、L表示）．试卷八上期中数学答案一．选择题二. 填空题11.4a、4614x y 12. 1440°、35 13. 等腰14. 615. 斜边、直角边(HL) 16. 8 17. 18 18. 3三．解答题19.角平分线、线段垂直平分线各2分，点出交点1分，答题1分。

北京市海淀区2020—2021年初二上期末统考数学试卷及答案数 学 试 卷（分数：100分 时刻：90分钟） 2020.1班级 姓名 学号 成绩 一、选择题（本题共30分，每小题3分）在下列各题的4个备选答案中，只有一个．．符合题意，请将正确选项前的字母填在表格中相应的位置． 题号 1 2 3 4 5 6 7 8 9 10 答案1．下列交通标志是轴对称图形的是（ ）A ．B ．C ．D ． 2．下列运算中正确的是（ ） A ． 532a a a =⋅ B ．()532a a = C ．326a a a =÷ D ．10552a a a =+3．下列长度的三条线段能组成直角三角形的是（ ）A ．1，2，3B ． 2，3，4C ． 3，4，5D ．4，5，6 4．下列二次根式中，是最简二次根式的是（ ） A ．21B ．3C ． 8D ． 9 5．在平面直角坐标系xOy 中，点P （2，1）关于y 轴对称的点的坐标是（ ） A ． （－2 ，1 ） B ． （ 2 ，1 ） C ． （－2 ，－1） D ． （2 ，－1） 6．已知图中的两个三角形全等，则∠1等于（ ） A ． 72° B ． 60° C ． 50° D ． 58°1b ab a72°50°7．若分式112--x x 的值为0，则x 的值为（ ）A ．1B ．－1C ．0D ． 1± 8．已知等腰三角形的一边长为4，另一边长为8，则它的周长是（ ）A ． 12B ． 16C ． 20D ． 16或20 9．从边长为a 的大正方形纸板中挖去一个边长为b 的小正方形后，将其裁成四个相同的等腰梯形（如图(1)），然后拼成一个平行四边形（如图(2)），那么通过运算两个图形阴影部分的面积，能够验证成立的公式为（ ）A ．222()a b a b -=-B ．222()2a b a ab b +=++C ．222()2a b a ab b -=-+D ．22()()a b a b a b -=+-10.如图(1)是长方形纸带，α=∠DEF ，将纸带沿EF 折叠成图(2)，再沿BF 折叠成图(3)， 则图(3)中的CFE ∠的度数是（ ）FGEGFFEE DDD CCCBBBA A A图(1) 图(2) 图(3)A ．α2B ． α290+︒C ．α2180-︒D ． α3180-︒ 二、填空题（本题共18分，每小题3分）11．若1-x 有意义，则x 的取值范畴是 ． 12．分解因式：=+-3632x x ．13．运算：222⎪⎭⎫⎝⎛÷a b b a = ．14．若实数a 、b 满足()0422=-++b a ，则=ba． 15．如图，等边△ABC 中，AB = 2, AD 平分∠BAC 交BC 于D ,则线段AD 的长为 ．16．下面是一个按某种规律排列的数阵：1 第1行2第2行3 11 32 第3行图（1） 图（2）DCBA13 14 15 4 17 23 19 52第4行依照数阵排列的规律，第5行从左向右数第3个数是 ，第n （3≥n 且n是整数）行从左向右数第2-n 个数是 （用含n 的代数式表示）． 三、解答题（本题共19分，第20题4分，其余每小题5分）17011(2013)()2---+18．如图,在△ABC 中，AB =AC , D 是BC 的中点，DE ⊥AB 于E ，DF ⊥AC 于F ．求证：DE =DF ．B19．已知0342=--x x ，求代数式()()()2232y y x y x x --+--的值．20．如图，电信部门要在公路m,n 之间的S 区域修建一座电视信号发射塔P ．按照设计要求,发射塔P 到区域S 内的两个城镇A ,B 的距离必须相等,到两条公路m ，n 的距离也必须相等．发射塔P 建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹) ．四、解答题（本题共20分，每小题5分） 21．解方程： 3221+=x x22．先化简，再求值：121112++÷⎪⎭⎫ ⎝⎛+-a a aa ，其中13-=a ．23．小明是学校图书馆A 书库的理想者，小伟是学校图书馆B 书库的理想者，他们各自负责本书库读者当天还回图书的整理工作．已知某天图书馆A 书库恰有120册图书需整理， 而B 书库恰有80册图书需整理，小明每小时整理图书的数量是小伟每小时整理图书数量的1.2倍，他们同时开始工作，结果小伟比小明提早15 分钟完成工作．求小明和小伟每小时分别能够整理多少册图书？24．在△ABC 中，AD 平分∠BAC ，BD ⊥AD ，垂足为D ，过D 作DE ∥AC ，交AB 于E ，若AB=5，求线段DE 的长．五、解答题（本题共13分，第25题6分，第26题7分） 25． 阅读材料1：关于两个正实数,a b ，由于()02≥-ba ，因此()()0222≥+⋅-b b a a ，即02≥+-b ab a ，因此得到ab b a 2≥+，同时当ab =时，a b +=． 阅读材料2：若0x >，则22111x x x x x x x +=+=+，因为10,0x x>>，因此由阅读材料1可得，2121=⋅≥+x x x x ，即21x x +的最小值是2，只有1x x=时，即1x =时取得最小值．依照以上阅读材料，请回答以下问题： （1）比较大小：21x + 2x （其中1x ≥）； 1x x+2-（其中1x <-）（2）已知代数式2331x x x +++变形为11x n x +++，求常数n 的值；（3）当x = 时，133+++x xx 有最小值，最小值为 . （直截了当写出答案）26．在四边形ABDE 中，C 是BD 边的中点．（1）如图(1)，若AC 平分BAE ∠，ACE ∠=90°,则线段AE 、AB 、DE 的长度满足的数量关系为 ；（直截了当写出答案）（2）如图（2），AC 平分BAE ∠， EC 平分AED ∠，若120ACE ∠=︒，则线段AB 、BD 、DE 、AE 的长度满足如何样的数量关系？写出结论并证明；（3）如图（3），BD = 8，AB =2，DE =8，135ACE ∠=︒，则线段AE 长度的最大值是____________（直截了当写出答案）．EDCBA图（3）EDC BA图（2）EDC BA图（1）海淀区八年级第一学期期末练习数学参考答案及评分标准 2020.1一、选择题（本题共30分，每小题3分）三、解答题（本题共19分，第20题4分，其余每小题5分） 17．解：原式=21332+-+----------------------------------4分=133+ ------------------------------------5分18．解法一：∵D 是BC 的中点，∴BD=CD . ------------------------------1分 ∵DE ⊥AB 于E ，DF ⊥AC 于F ，∴∠BED=∠CFD=90° . ---------------------------------------2分 ∵AB =AC ，∴ ∠B=∠C . ---------------------------------------3分∵ △BED 和△CFD 中⎪⎩⎪⎨⎧=∠=∠∠=∠CD BD C B CFDBED∴△BED ≌△CFD . ------------------------------------------------4分 ∴DE =DF . ----------------------------------------------------------5分解法二： 连接AD .∵在△ABC 中， AB =AC ，D 是BC 的中点，∴AD 平分∠BAC . --------------------------------------------------3分 ∵DE ⊥AB 于E ，DF ⊥AC 于F ，∴DE =DF . ----------------------------------------------------------5分 19．解：原式=()()22229124yyx x x ---+-=22229124y y x x x -+-+-=91232+-x x ------------------------------------------------------------------------------3分B∵0342=--x x ，∴342=-x x∴原式=()189339432=+⨯=+-x x ．----------------------------------------------------------5分20．作图痕迹：线段AB 的垂直平分线的作图痕迹2分覆盖区域S 的直线m 与n 的夹角的角平分线作图痕迹2分． （未标出点P 扣一分）四、解答题（本题共20分，每小题5分） 21．解：方程两边同乘()32+x x ，得：x x 43=+----------------------------------------------------------2分解那个整式方程，得：1=x --------------------------------------------------------------4分检验：当1=x 时，()()0311232≠+⨯⨯=+x x ,∴原方程的解是1=x ．------------------------------------------------------------5分 22．解：原式=1211112++÷⎪⎭⎫⎝⎛+-++a a a a a a =121112++÷+-+a a a a a =()a a a a 211+⋅+ =1+a ------------------------------------------------------------4分当13-=a 时，原式=3113=+-．---------------------------------------5分23．解：设小伟每小时能够整理x 册图书,则小明每小时能够整理1.2x 册图书.60158021120+=x x .-------------------------------------------------------2分 解得: 80=x ----------------------------------------------------3分 经检验80=x 是原方程的解且符合实际．-----------------------4分96802121=⨯=.x .答：小伟每小时能够整理80册图书,小明每小时能够整理96册图书. -----------5分24．解：∵AD 平分∠BAC ，∴∠1=∠2 .∵DE ∥AC ∴ ∠2=∠ADE .∴ ∠1=∠ADE .∴AE =DE .-------------------------------------------------------3分 ∵AD ⊥DB ，∴∠ADB =90°∴∠1+∠ABD =90°，∠ADE +∠BDE =∠ADB =90°，21<∴∠ABD =∠BDE .∴DE =BE .--------------------------------------------------------4分 ∵AB=5∴DE =BE= AE=5252121.AB =⨯=.------------------5分 五、解答题（本题共13分，第25题6分，第26题7分）25．（1）比较大小： 21x + ≥ 2x （其中1x ≥）； 1x x +____2-（其中1x <-）---------2分 （2）解： 111332+++=+++x n x x x x()()1111121+++=+++++x n x x x x x 11112+++=+++x n x x x ∴2=n --------------------------------------------4分 （3）当x = 0 时，133+++x xx 有最小值，最小值为 3 . （直截了当写出答案）---6分26．（1） AE=AB+DE ； ------------1分 （2）解：猜想：AE =AB+DE +BD 21．------------2分 证明：在AE 上取点F ，使AF =AB ，连结CF ， 在AE 上取点G ，使EG =ED ，连结CG ．∵C 是BD 边的中点，∴CB =CD=BD 21．∵AC 平分BAE ∠，∴∠BAC =∠F AC ．∵AF =AB ，AC =AC ，∴△ABC ≌△AFC .∴CF =CB ，∴∠BCA =∠FCA ．----------------------------4分同理可证：CD =CG ，∴∠DCE =∠GCE ． ∵CB =CD ，∴CG =CF∵120ACE ∠=︒，∴∠BCA +∠DCE=180°-120°=60°．图（2）∴∠FCA +∠GCE=60°．∴∠FCG=60°．∴△FGC 是等边三角形．-------------------------5分 ∴FG =FC=BD 21． ∵AE =AF+EG+FG ． ∴AE =AB+DE +BD 21．-----------------------6分 （3）2410+． ----------------7分说明：其它正确解法按相应步骤给分.EDCBA图（3）EDC BA图（1）G FEDCBA。

2020-2021学年北京市海淀实验中学八年级（上）期中数学试卷一、选择题（共10小题：共30分）1．（3分）第24届冬季奥林匹克运动会，将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）A．B．C．D．2．（3分）下列计算中，正确的是（）A．（a2）3＝a8B．a8÷a4＝a2C．a3+a2＝a5D．a2•a3＝a5 3．（3分）一个多边形的内角和是外角和的2倍，这个多边形是（）A．四边形B．五边形C．六边形D．八边形4．（3分）计算（x﹣k）（x+3）的结果中不含x的一次项，则k的值是（）A．0B．3C．﹣3D．﹣25．（3分）已知一个等腰三角形两边长分别为5，6，那么它的周长为（）A．16B．17C．16或17D．10或126．（3分）一副三角板，如图所示叠放在一起，则图中∠α的度数为（）A．75°B．60°C．65°D．55°7．（3分）如图，已知△ABC是等边三角形，点O是BC上任意一点，OE，OF分别于两边垂直，等边三角形的高为2，则OE+OF的值为（）A．1B．3C．2D．48．（3分）从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（）A．a2﹣b2＝（a﹣b）2B．（a+b）2＝a2+2ab+b2C．（a﹣b）2＝a2﹣2ab+b2D．a2﹣b2＝（a+b）（a﹣b）9．（3分）如图，在平面直角坐标系xOy中，△ABC的顶点C（3，﹣1），则点C关于x 轴、y轴对称的点的坐标分别为（）A．（3，1），（﹣3，﹣1）B．（﹣3，1），（﹣3，﹣1）C．（3，1），（1，3）D．（﹣3，﹣1），（3，1）10．（3分）在等边三角形ABC中，D，E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在（）A．△ABC的重心处B．AD的中点处C．A点处D．D点处二、填空题（共8小题；共24分）11．（3分）计算：（ab2）2÷（﹣ab）2＝．12．（3分）等式（a+b）2＝a2+b2成立的条件为．13．（3分）已知：如图，在△ABC中，点D在BC上，∠B＝40°，∠B＝∠BAD，∠C＝∠ADC，则∠DAC的度数为．14．（3分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝15°，AB的垂直平分线与AC交于点D，与AB交于点E，连接BD．若AD＝12cm，则BC的长为cm．15．（3分）若x2﹣（m﹣1）x+36是一个完全平方式，则m的值为．16．（3分）如果实数a，b满足a+b＝6，ab＝8，那么a2+b2＝．17．（3分）教材中有如下一段文字：思考如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC，固定住长木棍，转动短木棍，得到△ABD，这个实验说明了什么？如图中的△ABC与△ABD满足两边和其中一边的对角分别相等，即AB＝AB，AC＝AD ，∠B＝∠B，但△ABC与△ABD不全等．这说明，有两边和其中一边的对角分别相等的两个三角形不一定全等．小明通过对上述问题的再思考，提出：两边分别相等且这两边中较大边所对的角相等的两个三角形全等．请你判断小明的说法．（填“正确”或“不正确”）18．（3分）在数学课上，老师提出用尺规作图解决问题．已知：线段AB、线段AC，AB＞AC，在AB上求作点D，使△ACD的周长等于线段AB 的长．小左同学的作法如下：（1）在线段AB上截取BE＝AC；（2）连接CE，作线段CE的垂直平分线交AB于点D．老师说：“小左同学的作法正确．”请回答：小左同学的作图依据是．三、解答题（共7小题：共46分，第19题10分，第20-22题，每题5分）.19．（10分）计算：（1）（4a3b+6a2b2﹣ab3）÷2ab．（2）（3x+2）（2x2﹣x+1）．20．（5分）如图，点D、E在△ABC的BC边上，AB＝AC，AD＝AE．求证：BD＝CE．21．（5分）已知x2﹣4x﹣1＝0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．22．（5分）在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB 于E，若AB＝5，求线段DE的长．23．（7分）如图1，我们在2016年1月的日历中标出一个十字星，并计算它的“十字差”（将十字星左右两数，上下两数分别相乘再将所得的积作差，称为该十字星的“十字差”）．该十字星的十字差为12×14﹣6×20＝48，再选择其它位置的十字星，可以发现“十字差”仍为48．（1）如图2，将正整数依次填入5列的长方形数表中，探究不同位置十字星的“十字差”，可以发现相应的“十字差”也是一个定值，则这个定值为．（2）若将正整数依次填入k列的长方形数表中（k≥3），继续前面的探究，可以发现相应“十字差”为与列数k有关的定值，请用k表示出这个定值，并证明你的结论．（3）如图3，将正整数依次填入三角形的数表中，探究不同十字星的“十字差”，若某个十字星中心的数在第32行，且其相应的“十字差”为2015，则这个十字星中心的数为（直接写出结果）．24．（7分）如图，已知等腰三角形ABC中，∠BAC＝30°，AB＝AC，∠P AB＝α，作点B 关于直线AP的对称点为点D，连接AD，连接BD交AP于点G，连接CD交AP于点E ，交AB于点F．（1）如图（1）当α＝15°时，①按要求画出图形，②求出∠ACD的度数，③探究DE与BF的倍数关系并加以证明；（2）在直线AP绕点A顺时针旋转的过程中（0°＜a＜75°），当△AEF为等腰三角形时，利用下页备用图直接求出α的值为．25．（7分）我们把正n边形（n≥3）的各边三等分，分别以居中的那条线段为一边向外作正n边形，并去掉居中的那条线段，得到一个新的图形叫做正n边形的“扩展图形”，并将它的边数记为a n．如图1，将正三角形进行上述操作后得到其“扩展图形”，且a3＝12．图3、图4分别是正五边形、正六边形的“扩展图形”．（1）如图2，在5×5的正方形网格中用较粗的虚线画有一个正方形，请在图2中用实线画出此正方形的“扩展图形”；（2）已知a3＝12，a4＝20，a5＝30，则图4中a6＝，根据以上规律，正n边形的“扩展图形”中a n＝；（用含n的式子表示）（3）已知＝﹣，＝﹣，＝﹣，…，且+++…+＝，则n＝．2020-2021学年北京市海淀实验中学八年级（上）期中数学试卷参考答案与试题解析一、选择题（共10小题：共30分）1．（3分）第24届冬季奥林匹克运动会，将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）A．B．C．D．【解答】解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项正确；故选：D．2．（3分）下列计算中，正确的是（）A．（a2）3＝a8B．a8÷a4＝a2C．a3+a2＝a5D．a2•a3＝a5【解答】解：A、幂的乘方底数不变指数相乘，故A错误；B、同底数幂的除法底数不变指数相减，故B错误；C、不是同底数幂的乘法指数不能相加，故C错误；D、同底数幂的乘法底数不变指数相加，故D正确；故选：D．3．（3分）一个多边形的内角和是外角和的2倍，这个多边形是（）A．四边形B．五边形C．六边形D．八边形【解答】解：设所求多边形边数为n，由题意得（n﹣2）•180°＝360°×2解得n＝6．则这个多边形是六边形．故选：C．4．（3分）计算（x﹣k）（x+3）的结果中不含x的一次项，则k的值是（）A．0B．3C．﹣3D．﹣2【解答】解：（x﹣k）（x+3）＝x2﹣kx+3x﹣3k＝x2+（3﹣k）x﹣3k．∵（x﹣k）（x+3）的结果中不含x的一次项，∴3﹣k＝0．∴k＝3．故选：B．5．（3分）已知一个等腰三角形两边长分别为5，6，那么它的周长为（）A．16B．17C．16或17D．10或12【解答】解：当腰为6时，则三角形的三边长分别为6、6、5，满足三角形的三边关系，周长为17；当腰为5时，则三角形的三边长分别为5、5、6，满足三角形的三边关系，周长为16；综上可知，等腰三角形的周长为16或17．故选：C．6．（3分）一副三角板，如图所示叠放在一起，则图中∠α的度数为（）A．75°B．60°C．65°D．55°【解答】解：如图，∵∠1＝60°，∠2＝45°，∴∠α＝180°﹣45°﹣60°＝75°，故选：A．7．（3分）如图，已知△ABC是等边三角形，点O是BC上任意一点，OE，OF分别于两边垂直，等边三角形的高为2，则OE+OF的值为（）A．1B．3C．2D．4【解答】解：∵△ABC是等边三角形，∴AB＝BC＝AC，∠A＝∠B＝∠C＝60°又∵OE⊥AB，OF⊥AC，∠B＝∠C＝60°，∴OE＝OB•sin60°＝OB，同理OF＝OC．∴OE+OF＝（OB+OC）＝BC．在等边△ABC中，高h＝AB＝BC．∴OE+OF＝h．又∵等边三角形的高为2，∴OE+OF＝2，解法二：三角形ABC的面积等于三角形AOB的面积+三角形AOC的面积，三角形ABC 是等边三角形，所以三个三角形是等底，高OF+高OE等于三角形ABC的高2．故选：C．8．（3分）从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（）A．a2﹣b2＝（a﹣b）2B．（a+b）2＝a2+2ab+b2C．（a﹣b）2＝a2﹣2ab+b2D．a2﹣b2＝（a+b）（a﹣b）【解答】解：由图1将小正方形一边向两方延长，得到两个梯形的高，两条高的和为a ﹣b，即平行四边形的高为a﹣b，∵两个图中的阴影部分的面积相等，即甲的面积＝a2﹣b2，乙的面积＝（a+b）（a﹣b）．即：a2﹣b2＝（a+b）（a﹣b）．所以验证成立的公式为：a2﹣b2＝（a+b）（a﹣b）．故选：D．9．（3分）如图，在平面直角坐标系xOy中，△ABC的顶点C（3，﹣1），则点C关于x 轴、y轴对称的点的坐标分别为（）A．（3，1），（﹣3，﹣1）B．（﹣3，1），（﹣3，﹣1）C．（3，1），（1，3）D．（﹣3，﹣1），（3，1）【解答】解：∵在平面直角坐标系xOy中，△ABC的顶点C（3，﹣1），∴点C关于x轴、y轴对称的点的坐标分别为（3，1），（﹣3，﹣1）．故选：A．10．（3分）在等边三角形ABC中，D，E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在（）A．△ABC的重心处B．AD的中点处C．A点处D．D点处【解答】解：连接BP，∵△ABC是等边三角形，D是BC的中点，∴AD是BC的垂直平分线，∴PB＝PC，△PCE的周长＝EC+EP+PC＝EC+EP+BP，当B、P、E在同一直线上时，△PCE的周长最小，∵BE为中线，∴点P为△ABC的重心，故选：A．二、填空题（共8小题；共24分）11．（3分）计算：（ab2）2÷（﹣ab）2＝b2．【解答】解：（ab2）2÷（﹣ab）2＝a2b4÷a2b2＝b2．故答案为：b2．12．（3分）等式（a+b）2＝a2+b2成立的条件为ab＝0．【解答】解：∵（a+b）2＝a2+2ab+b2，∴等式（a+b）2＝a2+b2成立的条件为ab＝0，故答案为：ab＝0．13．（3分）已知：如图，在△ABC中，点D在BC上，∠B＝40°，∠B＝∠BAD，∠C＝∠ADC，则∠DAC的度数为20°．【解答】解：∵∠B＝∠BAD＝40°，∠ADC＝∠B+∠BAD，∴∠ADC＝80°，∴∠C＝∠ADC＝80°，∴∠DAC＝180°﹣160°＝20°，故答案为20°．14．（3分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝15°，AB的垂直平分线与AC交于点D，与AB交于点E，连接BD．若AD＝12cm，则BC的长为6cm．【解答】解：∵DE是AB的垂直平分线，∴AD＝BD＝12cm，∴∠A＝∠ABD＝15°，∴∠BDC＝∠A+∠ABD＝15°+15°＝30°，在Rt△BCD中，BC＝BD＝×12＝6cm．故答案为：6．15．（3分）若x2﹣（m﹣1）x+36是一个完全平方式，则m的值为﹣11或13．【解答】解：∵x2﹣（m﹣1）x+36是一个完全平方式，∴m﹣1＝±12，故m的值为﹣11或13，故答案为：﹣11或1316．（3分）如果实数a，b满足a+b＝6，ab＝8，那么a2+b2＝20．【解答】解：∵a+b＝6，ab＝8，∴a2+b2＝（a+b）2﹣2ab＝36﹣16＝20，故答案为：2017．（3分）教材中有如下一段文字：思考如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC，固定住长木棍，转动短木棍，得到△ABD，这个实验说明了什么？如图中的△ABC与△ABD满足两边和其中一边的对角分别相等，即AB＝AB，AC＝AD ，∠B＝∠B，但△ABC与△ABD不全等．这说明，有两边和其中一边的对角分别相等的两个三角形不一定全等．小明通过对上述问题的再思考，提出：两边分别相等且这两边中较大边所对的角相等的两个三角形全等．请你判断小明的说法正确．（填“正确”或“不正确”）【解答】解：小明的说法正确．理由：如图，△ABC和△DEF中，AB＞AC，ED＞DF，AB＝DE，AC＝DF，∠ACB＝∠DFE，作AG⊥BC于G，DH⊥EF于H．∵∠ACB＝∠DFE，∴∠ACG＝∠DFH，在△ACG和△DFH中，，∴△ACG≌△DFH，∴AG＝DH，在Rt△ABG和Rt△DEH中，，∴△ABG≌△DEH，∴∠B＝∠E，在△ABC和△DEF中，，∴△ABC≌△DEF．（当△ABC和△DEF是锐角三角形时，证明方法类似）．故答案为正确．18．（3分）在数学课上，老师提出用尺规作图解决问题．已知：线段AB、线段AC，AB＞AC，在AB上求作点D，使△ACD的周长等于线段AB 的长．小左同学的作法如下：（1）在线段AB上截取BE＝AC；（2）连接CE，作线段CE的垂直平分线交AB于点D．老师说：“小左同学的作法正确．”请回答：小左同学的作图依据是线段垂直平分线上的点到这条线段两端点的距离相等．【解答】解：由作法得D点线段CE的垂直平分线上，根据线段垂直平分线上的点到这条线段两端点的距离相等，∴DE＝DC，而BE＝AC，∴△ACD的周长＝AC+AD+CD＝AC+AD+DE＝BE+AE＝AB．故答案为线段垂直平分线上的点到这条线段两端点的距离相等．三、解答题（共7小题：共46分，第19题10分，第20-22题，每题5分）.19．（10分）计算：（1）（4a3b+6a2b2﹣ab3）÷2ab．（2）（3x+2）（2x2﹣x+1）．【解答】解：（1）原式＝2a2+3ab﹣b2；（2）原式＝6x3﹣3x2+3x+4x2﹣2x+2＝6x3+x2+x+2．20．（5分）如图，点D、E在△ABC的BC边上，AB＝AC，AD＝AE．求证：BD＝CE．【解答】证明：如图，过点A作AP⊥BC于P．∵AB＝AC，∴BP＝PC；∵AD＝AE，∴DP＝PE，∴BP﹣DP＝PC﹣PE，∴BD＝CE．21．（5分）已知x2﹣4x﹣1＝0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．【解答】解：∵x2﹣4x﹣1＝0，即x2﹣4x＝1，∴原式＝4x2﹣12x+9﹣x2+y2﹣y2＝3x2﹣12x+9＝3（x2﹣4x）+9＝3+9＝12．22．（5分）在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB 于E，若AB＝5，求线段DE的长．【解答】解：∵AD平分∠BAC，∴∠BAD＝∠CAD，∵DE∥AC，∴∠CAD＝∠ADE，∴∠BAD＝∠ADE，∴AE＝DE，∵AD⊥DB，∴∠ADB＝90°，∴∠EAD+∠ABD＝90°，∠ADE+∠BDE＝∠ADB＝90°，∴∠ABD＝∠BDE，∴DE＝BE，∵AB＝5，∴DE＝BE＝AE＝AB＝2.5．23．（7分）如图1，我们在2016年1月的日历中标出一个十字星，并计算它的“十字差”（将十字星左右两数，上下两数分别相乘再将所得的积作差，称为该十字星的“十字差”）．该十字星的十字差为12×14﹣6×20＝48，再选择其它位置的十字星，可以发现“十字差”仍为48．（1）如图2，将正整数依次填入5列的长方形数表中，探究不同位置十字星的“十字差”，可以发现相应的“十字差”也是一个定值，则这个定值为24．（2）若将正整数依次填入k列的长方形数表中（k≥3），继续前面的探究，可以发现相应“十字差”为与列数k有关的定值，请用k表示出这个定值，并证明你的结论．（3）如图3，将正整数依次填入三角形的数表中，探究不同十字星的“十字差”，若某个十字星中心的数在第32行，且其相应的“十字差”为2015，则这个十字星中心的数为976（直接写出结果）．【解答】解：（1）根据题意得：6×8﹣2×12＝48﹣24＝24；故答案为：24；（2）定值为k2﹣1＝（k+1）（k﹣1）；证明：设十字星中心的数为x，则十字星左右两数分别为x﹣1，x+1，上下两数分别为x ﹣k，x+k（k≥3），十字差为（x﹣1）（x+1）﹣（x﹣k）（x+k）＝x2﹣1﹣x2+k2＝k2﹣1，故这个定值为k2﹣1＝（k+1）（k﹣1）；（3）设正中间的数为a，则上下两个数为a﹣62，a+64，左右两个数为a﹣1，a+1，根据题意得：（a﹣1）（a+1）﹣（a﹣62）（a+64）＝2015，解得：a＝976．故答案为：976．24．（7分）如图，已知等腰三角形ABC中，∠BAC＝30°，AB＝AC，∠P AB＝α，作点B 关于直线AP的对称点为点D，连接AD，连接BD交AP于点G，连接CD交AP于点E ，交AB于点F．（1）如图（1）当α＝15°时，①按要求画出图形，②求出∠ACD的度数，③探究DE与BF的倍数关系并加以证明；（2）在直线AP绕点A顺时针旋转的过程中（0°＜a＜75°），当△AEF为等腰三角形时，利用下页备用图直接求出α的值为30°或52.5°．【解答】解：（1）①如图1：②∵B、D关于AP对称，∴AP垂直平分BD，a＝15°，∴AD＝AB，∠1＝∠2＝15°，∵∠BAC＝30°，∴∠DAC＝∠1+∠2+∠BAC＝60°，∵AC＝AB，∴AC＝AD，∴△ACD为等边三角形∴∠ACD＝60°．③DE＝2BF，证明：连接EB，∵AP垂直平分BD，∴ED＝EB，∴∠3＝∠4，∵AB＝AD，∠DAB＝30°，∴∠ADB＝75°，又∠ADC＝60°，∴∠3＝∠4＝15°，∴∠5＝30°，又AD＝AC，AB平分∠DAC，∴AB⊥DC，∴EB＝2BF，∴ED＝2BF．（2）如图2，∵AD＝AC，∴△DAC是等腰三角形∴∠ADC＝（180°﹣2a﹣30°）÷2＝75°﹣a，∴∠AEF＝∠ADC+∠DAE＝75°﹣a+a＝75°，当AE＝AF时，∠EAF＝a＝180°﹣75°×2＝180°﹣150°＝30°；当AE＝EF时，∠EAF＝a＝（180°﹣75°）÷2＝52.5°；当EF＝AF时，∠AEF＝∠EAF＝a＝75°（舍去）．故答案为：30°或52.5°．25．（7分）我们把正n边形（n≥3）的各边三等分，分别以居中的那条线段为一边向外作正n边形，并去掉居中的那条线段，得到一个新的图形叫做正n边形的“扩展图形”，并将它的边数记为a n．如图1，将正三角形进行上述操作后得到其“扩展图形”，且a3＝12．图3、图4分别是正五边形、正六边形的“扩展图形”．（1）如图2，在5×5的正方形网格中用较粗的虚线画有一个正方形，请在图2中用实线画出此正方形的“扩展图形”；（2）已知a3＝12，a4＝20，a5＝30，则图4中a6＝42，根据以上规律，正n边形的“扩展图形”中a n＝n（n+1）；（用含n的式子表示）（3）已知＝﹣，＝﹣，＝﹣，…，且+++…+＝，则n＝99．【解答】解：（1）如图所示：（2）图4中a6＝6×7＝42，根据以上规律，正n边形的“扩展图形”中a n＝n（n+1）；（用含n的式子表示）（3）∵＝﹣，＝﹣，＝﹣，…，且+++…+＝，∴﹣＝，解得n＝99．故答案为：42，n（n+1）；99．。