知识点4-4 基带传输的常用码型.
- 格式:ppt
- 大小:365.50 KB
- 文档页数:7
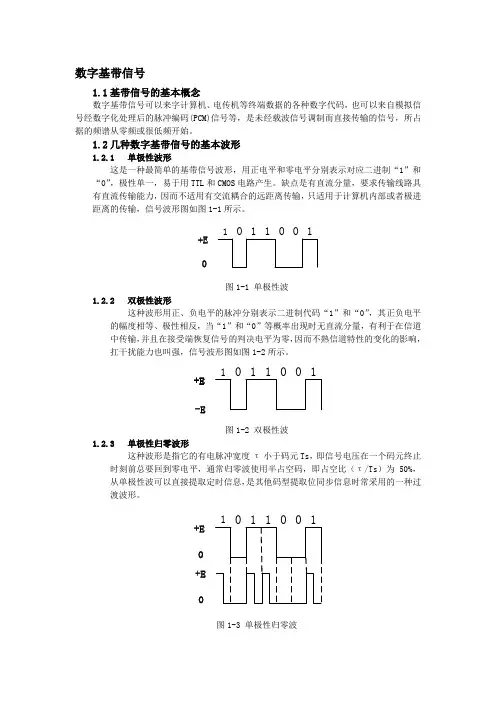
数字基带信号1.1 基带信号的基本概念数字基带信号可以来字计算机、电传机等终端数据的各种数字代码,也可以来自模拟信号经数字化处理后的脉冲编码(PCM)信号等,是未经载波信号调制而直接传输的信号,所占据的频谱从零频或很低频开始。
1.2 几种数字基带信号的基本波形1.2.1 单极性波形这是一种最简单的基带信号波形,用正电平和零电平分别表示对应二进制“1”和“0”,极性单一,易于用TTL 和CMOS 电路产生。
缺点是有直流分量,要求传输线路具有直流传输能力,因而不适用有交流耦合的远距离传输,只适用于计算机内部或者极进距离的传输,信号波形图如图1-1所示。
1 011100+E图1-1 单极性波1.2.2 双极性波形这种波形用正、负电平的脉冲分别表示二进制代码“1”和“0”,其正负电平的幅度相等、极性相反,当“1”和“0”等概率出现时无直流分量,有利于在信道中传输,并且在接受端恢复信号的判决电平为零,因而不熟信道特性的变化的影响,扛干扰能力也叫强,信号波形图如图1-2所示。
1 011100+E-E图1-2 双极性波1.2.3 单极性归零波形这种波形是指它的有电脉冲宽度τ小于码元Ts ,即信号电压在一个码元终止时刻前总要回到零电平,通常归零波使用半占空码,即占空比(τ/Ts )为50%,从单极性波可以直接提取定时信息,是其他码型提取位同步信息时常采用的一种过渡波形。
1 011100+E+E图1-3 单极性归零波1.2.4 双极性归零波形这种波形兼有双极性和归零波形的特点,由于其相邻脉冲之间存在零电位的间隔,是的接受端很容易识别出每个码元的起止时间,从而使收发双方能保持位的同步。
波形如图1-4所示。
1 011100+E-E+E-E图1-4 双极性归零波1.2.5 差分波形这种波形是用相邻码元的电平的跳变和不变来表示消息代码,而与码元本身的点位或极性无关,电平跳变表示“1”,电平的不变表示“0”,当然这种规定也可以反过来,也称为相对码波形,而相应地称前面的单极性或双极性波形为绝对码波形,这种波形传输代码可以消除设备初始状态的影响。

基带信号的常见码型实验代码引言随着通信技术的发展和应用的普及,基带信号的处理变得越来越重要。
在通信领域中,基带信号是指未经过调制的信号,是数字数据或模拟信号的直接表达。
基带信号的常见码型是指在数字通信中常用的信号编码方式。
本文将详细探讨基带信号的常见码型实验代码。
1. 基带信号概述基带信号是指信号通过低通滤波器之后的信号。
它是一种携带有用信息的波形信号,可以表示为一个成对的实数或复数函数。
基带信号常用于数字通信系统中的数据传输和调制解调过程。
2. 基带信号的编码方式基带信号的编码方式有很多种,其中常见的包括:2.1 单极性非归零码(Unipolar Non-Return-to-Zero,UNRZ)单极性非归零码是一种简单的基带信号编码方式。
它的特点是使用一个电平表示数据位,0表示低电平,1表示高电平。
UNRZ码的优点是编码简单,缺点是抗干扰能力较差。
2.2 双极性非归零码(Bipolar Non-Return-to-Zero,BNRZ)双极性非归零码是一种使用正负电平表示数据位的基带信号编码方式。
它的特点是0表示低电平,1表示正负两种高电平。
BNRZ码的优点是抗干扰能力较好,缺点是在传输过程中可能产生直流分量。
2.3 单极性归零码(Unipolar Return-to-Zero,URZ)单极性归零码是一种使用正电平和零电平表示数据位的基带信号编码方式。
它的特点是每个数据位的中间位置都有一个归零点,以实现数据位的识别。
URZ码的优点是抗干扰能力较好,缺点是传输速率较低。
2.4 曼彻斯特编码(Manchester Coding)曼彻斯特编码是一种使用电平转变来表示数据位的基带信号编码方式。
它的特点是每个数据位都包含一个电平转变,0表示电平下降,1表示电平上升。
曼彻斯特编码的优点是时钟恢复容易,缺点是带宽利用率较低。
3. 基带信号码型实验代码为了实现基带信号的编码方式,我们可以使用编程语言编写相应的实验代码。



数字基带信号1.1 基带信号的基本概念数字基带信号可以来字计算机、电传机等终端数据的各种数字代码,也可以来自模拟信号经数字化处理后的脉冲编码(PCM)信号等,是未经载波信号调制而直接传输的信号,所占据的频谱从零频或很低频开始。
1.2 几种数字基带信号的基本波形1.2.1 单极性波形这是一种最简单的基带信号波形,用正电平和零电平分别表示对应二进制“1”和“0”,极性单一,易于用TTL 和CMOS 电路产生。
缺点是有直流分量,要求传输线路具有直流传输能力,因而不适用有交流耦合的远距离传输,只适用于计算机内部或者极进距离的传输,信号波形图如图1-1所示。
1 011100+E图1-1 单极性波1.2.2 双极性波形这种波形用正、负电平的脉冲分别表示二进制代码“1”和“0”,其正负电平的幅度相等、极性相反,当“1”和“0”等概率出现时无直流分量,有利于在信道中传输,并且在接受端恢复信号的判决电平为零,因而不熟信道特性的变化的影响,扛干扰能力也叫强,信号波形图如图1-2所示。
1 011100+E-E图1-2 双极性波1.2.3 单极性归零波形这种波形是指它的有电脉冲宽度τ小于码元Ts ,即信号电压在一个码元终止时刻前总要回到零电平,通常归零波使用半占空码,即占空比(τ/Ts )为50%,从单极性波可以直接提取定时信息,是其他码型提取位同步信息时常采用的一种过渡波形。
1 011100+E+E图1-3 单极性归零波1.2.4 双极性归零波形这种波形兼有双极性和归零波形的特点,由于其相邻脉冲之间存在零电位的间隔,是的接受端很容易识别出每个码元的起止时间,从而使收发双方能保持位的同步。
波形如图1-4所示。
1 011100+E-E+E-E图1-4 双极性归零波1.2.5 差分波形这种波形是用相邻码元的电平的跳变和不变来表示消息代码,而与码元本身的点位或极性无关,电平跳变表示“1”,电平的不变表示“0”,当然这种规定也可以反过来,也称为相对码波形,而相应地称前面的单极性或双极性波形为绝对码波形,这种波形传输代码可以消除设备初始状态的影响。
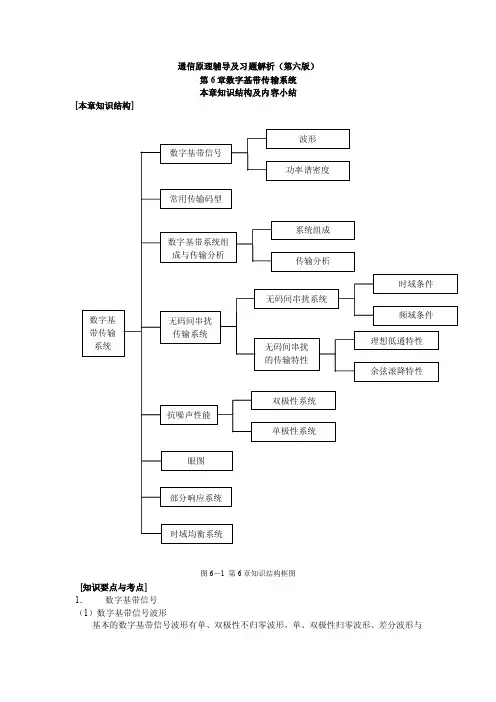
通信原理辅导及习题解析(第六版)第6章数字基带传输系统本章知识结构及内容小结[本章知识结构]图6-1 第6章知识结构框图[知识要点与考点]1.数字基带信号(1)数字基带信号波形基本的数字基带信号波形有单、双极性不归零波形,单、双极性归零波形、差分波形与多电平波形。
(2)数字基带信号的数学表达式 ①()()nsn s t a g t nT ∞=-∞=-∑式中,()s t 为单极性时,n a 取0或+1;()s t 为双极性时,n a 取+1或-1。
()g t 可取矩形 ②()()nn s t s t ∞=-∞=∑(3)数字基带信号的功率谱密度[]212212()(1)()()()(1)()()s s s s s s m P f f P P G f G f f PG mf P G mf f mf δ∞=-∞=--++--∑① 二进制数字基带信号的功率谱密度可能包含连续谱与离散谱。
其中,连续谱总是存在,根据连续谱确定信号带宽;在双极性等概信号时,离散谱不存在,根据离散谱确定直流分量与定时分量;② 二进制不归零基带信号的带宽为s f (1/s s f T =);二进制归零基带信号的带宽为1/τ。
2.常用传输码型常用传输码型有三电平码(AMI 码、HDB3码)与二电平码(双相码、差分双相码、密勒码、CMI 码、块编码)。
其中,AMI 码与HDB3码需要重点掌握。
(1)AMI 码将消息码的“1”(传号)交替地变换为“+1”和“-1”,而“0”(空号)保持不变。
(2)HDB3码 ① 编码规则:当连0数目不超过3个时,同AMI 码;连0数目超过3时,将每4个连“0”化作一小节,定义为B00V ;V 与前一个相邻的非0脉冲极性相同,相邻的V 码之间极性交替。
V 的取值为+1或-1;B 的取值可选0、+1或-1;V 码后面的传号码极性也要交替。
② 译码规则:寻找破坏脉冲V 码,即寻找两个相邻的同极性码,后一个码为V 码;V 码与其之前的3个码一起为4个连0码;将所有-1变成+1后便得到原消息代码。

基带传输编码的几种类型及特点概述及解释说明1. 引言1.1 概述基带传输编码是一种将数字数据转化为模拟形式以进行有效传输的技术。
它在通信领域被广泛应用,尤其是在信息传输和存储中起到关键的作用。
基带传输编码根据不同的需求和条件,可以采用多种类型,并且每种类型都具有不同的特点和适用情况。
1.2 文章结构本文将分为五个部分来介绍基带传输编码的几种类型及其特点。
首先,在引言部分我们将对基带传输编码进行简要介绍,并给出本文的目录结构。
接下来,在第二、三、四部分,我们将详细介绍基带传输编码类型一、二、三,并分析每种类型的特点。
最后,在结论部分,我们将对各种基带传输编码类型及其特点进行总结,并进行应用场景分析与比较,同时展望未来发展趋势。
1.3 目的本文主要旨在通过对基带传输编码不同类型及其特点进行综合概述和解释说明,为读者提供一个全面了解基带传输编码的指南。
通过阅读本文,读者能够掌握各种基带传输编码类型的基本原理和特点,以及它们在实际应用中的优缺点。
并且,本文还将通过分析不同编码类型的应用场景和比较优劣来帮助读者选择适合自己需求的基带传输编码方式。
最后,我们还将对基带传输编码未来的发展趋势进行展望,为读者提供一些思考和参考。
2. 基带传输编码类型一2.1 类型说明基带传输编码是一种将数字信号转换为模拟信号的技术,用于在通信系统中将数字数据进行传输。
基带传输编码类型主要包括非归零码和曼彻斯特编码。
非归零码是一种通过改变信号电平来表示二进制数据值的编码方式。
它的特点是在一个位周期内只有一次电平变换,而其他时间则保持固定的电平。
常见的非归零码有无反向非归零码(NRZ)和反向不归零码(RZ)两种。
其中,无反向非归零码将0表示为低电平、1表示为高电平,而反向不归零码则相反。
曼彻斯特编码是一种通过在一个位周期内进行两次电平变换来表示二进制数据值的编码方式。
它的特点是每个时钟周期都包含一个过渡点,从而提供了时钟同步机制。



基带传输中数据的表示方法
基带传输是指在数字通信中传输数据信号时,所采用的一种信号传输方式,也称为基本频带传输。
在基带传输中,数据信号直接在信道中传输,没有经过调制处理。
因此,在进行基带传输时,需要采用一种合适的数据表示方法,以便正确地传输数据信号。
数据的表示方法有很多种,其中常见的有二进制表示法、十进制表示法、十六进制表示法等。
在基带传输中,通常采用二进制表示法,因为数字信号只有两个状态,即0和1,与二进制的0和1相对应。
二进制表示法是将数据转换成由0和1组成的二进制数码来表示。
例如,数字7可以用二进制数码111来表示,数字0可以用二进制数码000来表示。
除了二进制表示法外,还有一种常用的数据表示方法叫做曼彻斯特编码。
曼彻斯特编码是一种线路编码方式,它将每个二进制位分为两个时隙,分别代表0和1。
具体来说,在曼彻斯特编码中,若数据位为0,则在时隙1中发送高电平,在时隙2中发送低电平;若数据位为1,则在时隙1中发送低电平,在时隙2中发送高电平。
曼彻斯特编码可以有效地降低误码率和时钟同步错误的发生概率,因此在基带传输中被广泛使用。
总之,在进行基带传输时,数据的表示方法是十分重要的。
不同的数
据表示方法具有不同的优缺点,需要根据实际情况选择合适的方法来进行数据传输。

基带传输的常用码型有:
1. 双极性不归零码:“1”码和“0”码都有电流,“1”为正电流,“0”为负电流,正和负的幅度相等,判决门限为零电平。
其优点是抗噪能力强一些,缺点是生成电路需要正负双电源供电。
2. 单极性不归零码:无电压表示“0”,恒定正电压表示“1”,每个码元时间的中间点是采样时间,判决门限为半幅电平。
单极性的优点是可以采用单电源供电,缺点是具有直流分量,只能在直流耦合的电路中使用。
3. 双极性归零码:在每一码元时间间隔内,当发“1”时,发出正向窄脉冲;当发“0”时,则发出负向窄脉冲。
两个码元的时间间隔可以大于每一个窄脉冲的宽度,取样时间是对准脉冲的中心。
4. 单极性归零码:在每一码元时间间隔内,有一半的时间发出正电流,而另一半时间则不发出电流表示二进制数“1”。
整个码元时间间隔内无电流发出表示二进制数“0”。
5. 曼彻斯特编码:在曼彻斯特编码中,每个二进制位(码元)的中间都有电压跳变。
用电压的正跳变表示“0”,电压的负跳变表示“1”。
此外,还有差分码、密勒码、CMI码、AMI码、HDB3码等基带传输的常用码型。
您可以咨询专业人士获取详细信息。
基带传输的常用码型1.传输码的码型选择原则(1)不含直流,低频分量尽量少;(2)含有丰富的定时信息,便于从接收码流中提取定时信号;(3)功率谱主瓣宽度窄,节省传输频带;(4)不受信息源统计特性的影响,能适应信息源的变化;(5)具有内在的检错能力,即码型应具有一定规律性;(6)编译码简单,以降低通信延时和成本。
2.几种常用的传输码型(1)AMI码①编码规则将消息码的“1”交替地变换为“+1”和“-1”,而“0”保持不变。
例如:②码型特点a.优点无直流成分,且高、低频分量少;能量集中在频率为码速处;编解码电路简单,可利用传号极性交替这一规律观察误码情况。
b.缺点当原信码出现长连“0”串时,信号的电平长时间不跳变,提取定时信号困难。
(2)HDB3码①编码规则a.检查消息码的连“0”个数。
当连“0”数小于等于3时,则利用AMI码编码规则;b.连“0”数目超过3个时,将第4个“0”改为非“0”脉冲,记为“+V”或“-V”,称为破坏脉冲;c.相邻V码的极性必须交替出现(确保无直流);d.满足(c)的条件下检查V的极性是否与前面一个非“0”脉冲的极性相同,若不同,将原连0码“0000”的第一个0改为B,B的取值与后面的V一致,B称为调节脉冲;e.V码后面的传号码极性也要交替。
例如:②码型特点a.HDB3码除具备AMI码的优点外,同时还将连“0”码限制在3个以内,保证接收端定时信息的提取;b.HDB3码的编码比较复杂,解码比较简单。
(3)双相码(曼彻斯特码)①编码规则“0”码用“01”两位码表示,“1”码用“10”两位码表示。
例如:例如:②码型特点优点:含丰富的位定时信息,无直流分量,编码过程简单。
缺点:占用带宽加倍,频带利用率降低,多适用于近距离的传输。
(4)差分双相码①编码规则每个码元的开始处是否存在跳变来确定信码。
有跳变则表示二进制“1”,无跳变则表示二进制“0”。
②码型特点解决双相码因极性反转引起的译码错误,适用于局域网中。
基带传输码型的基本要求
基带传输码型是一种数字通信中常用的编码方式,其基本要求包括以
下几个方面:
1. 可靠性:基带传输码型的编码方式应该能够保证数据的可靠传输,
即在传输过程中不会出现误码或丢失数据的情况。
为了实现可靠性,
通常会采用纠错码或者检错码等技术来进行数据的校验和纠错。
2. 带宽效率:基带传输码型的编码方式应该能够在保证可靠性的前提下,尽可能地提高数据传输的带宽效率。
为了实现带宽效率,通常会
采用压缩编码或者多级编码等技术来减少数据传输所需的带宽。
3. 实时性:基带传输码型的编码方式应该能够满足实时传输的要求,
即在传输过程中能够及时地传输数据,避免出现数据延迟或者卡顿的
情况。
为了实现实时性,通常会采用流控制或者缓存技术来控制数据
的传输速度和缓存数据的大小。
4. 兼容性:基带传输码型的编码方式应该能够兼容不同的传输媒介和
设备,以便在不同的环境下进行数据传输。
为了实现兼容性,通常会
采用标准化的编码方式和协议,以便不同的设备和系统能够进行互通。
总的来说,基带传输码型的基本要求是在保证数据可靠传输的前提下,尽可能地提高数据传输的带宽效率和实时性,同时兼容不同的传输媒
介和设备。
这些要求在数字通信中都是非常重要的,对于保障数据传
输的质量和效率都有着至关重要的作用。
一.基带传输截图及主要代码:2.主要代码主函数:#include "cmi.h"#include "hdb3.h"void main(){FILE *fs,*fami,*fmanchester,*fcmi,*fhdb3,*fdeami,*fdecmi,*fdemanchester;fs=fopen("code.cds","r");fami=fopen("ami.cds","w+r");fmanchester=fopen("manchester.cds","w+r");fhdb3=fopen("hdb3.cds","w+r");fcmi=fopen("cmi.cds","w+r");fdeami=fopen("deami.cds","w+r");fdecmi=fopen("decmi.cds","w+r");fdemanchester=fopen("demanchester.cds","w+r");fseek(fs,0,SEEK_END);amistream(fs,fami);fseek(fami,0,SEEK_SET);deamistream(fami,fdeami);fseek(fs,0,SEEK_SET);cmistream(fs,fcmi);fseek(fcmi,0,SEEK_SET);decmistream(fcmi,fdecmi);fseek(fs,0,SEEK_SET);manchstream(fs,fmanchester);fseek(fmanchester,0,SEEK_SET);demanchstream(fmanchester,fdemanchester);fclose(fs);fclose(fmanchester);fclose(fcmi);fclose(fami);fclose(fdeami);fclose(fdecmi);fclose(fdemanchester);}Ami函数部分:#include "ami.h"void ami(int n,FILE *file){if(n==0)fwrite("0",sizeof(char),1,file);else{t++;if(t%2==1)fwrite("2",sizeof(char),1,file);elsefwrite("1",sizeof(char),1,file);}}void deami(int n,FILE *file){if(n==0)fwrite("0",sizeof(char),1,file);if(n==1)fwrite("1",sizeof(char),1,file);if(n==2)fwrite("1",sizeof(char),1,file);}void amistream(FILE *filein,FILE *fileout) {long fstr;int i,k;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);ami(k,fileout);}}void deamistream(FILE *filein,FILE *fileout) {long fstr;int i,k;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);deami(k,fileout);}}Cmi函数部分:#include "cmi.h"void cmi(int n,FILE *file){if(n==0){fwrite("01",sizeof(char),2,file);}else{cmi_t++;if(cmi_t%2==0)fwrite("11",sizeof(char),2,file);elsefwrite("00",sizeof(char),2,file);}}void decmi(int m,int n,FILE *file){if((m+n)==2||(m+n)==0)fwrite("1",sizeof(char),1,file);if((m+n)==1)fwrite("0",sizeof(char),1,file);}void cmistream(FILE *filein,FILE *fileout){long fstr;int i,k;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);cmi(k,fileout);}}void decmistream(FILE *filein,FILE *fileout){long fstr;int i,k,l;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr/2;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);l=atoi(&ch);decmi(k,l,fileout);}}Manchester函数部分:#include "manchester.h"void manchester(int n,FILE *file){if(n==0){fwrite("0",sizeof(char),1,file);fwrite("1",sizeof(char),1,file);}else{fwrite("1",sizeof(char),1,file);fwrite("0",sizeof(char),1,file);}}void demanchester(int m,int n,FILE *file){if(m==1&&n==0)fwrite("1",sizeof(char),1,file);elsefwrite("0",sizeof(char),1,file);}void manchstream(FILE *filein,FILE *fileout) {long fstr;int i,k;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);manchester(k,fileout);}}void demanchstream(FILE *filein,FILE *fileout) {long fstr;int i,k,l;char ch;fseek(filein,0,SEEK_END);fstr=ftell(filein);fseek(filein,0,SEEK_SET);for(i=0;i<fstr/2;i++){memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);k=atoi(&ch);memset(&ch,NULL,sizeof(char));fread(&ch,1,1,filein);l=atoi(&ch);demanchester(k,l,fileout);}}二.DIF_FFT截图及主要代码:DIF_FFT结果截图2.主要代码:主函数:#include <iostream.h>#include <memory.h>#include "bichange.h"#include "reorder.h"#include "wchange.h"#include "bfchange.h"#include "linecal.h"#define N 1<<3void main(){int i,l,j,n,p;int d;/*int a[N];int b[N],c[N];int temp=0;a[0]=temp;cout<<a[0]<<" ";for(i=1;i<N;i++)//倒序测试{a[i]=reorder(temp,3);temp=a[i];cout<<a[i]<<" ";}cds x,y,z,w;x.i=1;x.j=0;y.i=1;y.j=0;z.i=0;z.j=8;wchange(0,8,&w.i,&w.j);//蝴蝶交换测试bfchange(&x,&y,w);memset(b,0,8);memset(c,0,8);*/cds A[N];cds temp;for(i=0;i<N;i++){A[i].i=A[i].j=1;}for(l=1;l<=3;l++){for(i=0;i<(1<<(3-l));i++){d=i*(1<<l);for(j=0;j<(1<<(l-1));j++){p=j;wchange(p,N,&temp.i,&temp.j);bfchange(&A[d],&A[d+(1<<(l-1))],temp);}}}}倒序主要代码:#include "reorder.h"int reorder(int n,int m){int temp,re;temp=bichange(n,m);temp++;re=bichange(temp,m);return re;}int bichange(int n,int m){int sum=0;int i;int a,b;for(i=1;i<m;i++){a=n/2;b=n%2;sum+=(1<<(m-i))*b;n=a;}sum=sum+n;return sum;}旋转因子:#include "wchange.h"void wchange(float p,float n,float *a,float *b)//a为实部,b为虚部{*a=(float)cos(2*pie*p/n);*b=(float)sin(2*pie*p/n);//cout<<*a<<" "<<*b;}蝴蝶运算:#include "bfchange.h"void bfchange(cds *x,cds *y,cds w){cds temp1,temp2;temp1.i=x->i+(y->i)*w.i-(y->j)*w.j;temp1.j=x->j+(y->i)*w.j+(y->j)*w.i;temp2.i=x->i-(y->i)*w.i+(y->j)*w.j;temp2.j=x->j-(y->i)*w.j-(y->j)*w.i;x->i=temp1.i;x->j=temp1.j;y->i=temp2.i;y->j=temp2.j;cout<<x->i<<x->j<<endl;cout<<y->i<<y->j<<endl;}。