第6章matlab数据分析与多项式计算_习题答案
- 格式：doc
- 大小：53.50 KB
- 文档页数：4
下载文档原格式
合集下载
《计量经济学》与MATLAB编程-第六章多项式回归与非线性回归
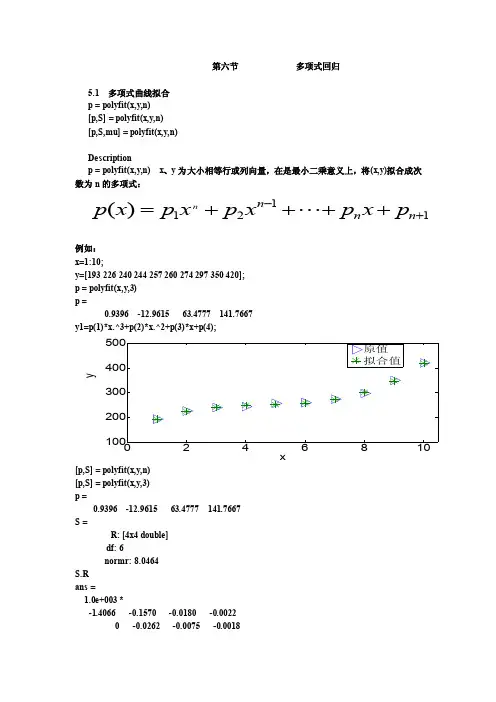
第六节 多项式回归5.1 多项式曲线拟合 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)Descriptionp = polyfit(x,y,n) x 、y 为大小相等行或列向量，在是最小二乘意义上，将(x,y)拟合成次数为n 的多项式：1121)(+-++++=n n n p x p x p x p x p n例如： x=1:10;y=[193 226 240 244 257 260 274 297 350 420]; p = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667y1=p(1)*x.^3+p(2)*x.^2+p(3)*x+p(4);xy[p,S] = polyfit(x,y,n) [p,S] = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667 S =R: [4x4 double] df: 6normr: 8.0464 S.R ans =1.0e+003 *-1.4066 -0.1570 -0.0180 -0.0022 0 -0.0262 -0.0075 -0.00180 0 -0.0019 -0.00140 0 0 0.0005normr是残差的模，即：norm(y-y1)ans =8.0464[p,S,MU] = polyfit(x,y,n)[p,S,MU] = polyfit(x,y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464MU =5.50003.0277MU是x均值和x的标准差即std(x)S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.0901P它等于：[p,S] = polyfit((x-mean(x))./std(x),y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464>> S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.09015.2 多项式估计y= polyval(p,x)[y,DELT A] = polyval(p,x,S)y= polyval(p,x) 返回给定系数p和变量x值的多项式的预测y = P(1)*x^N + P(2)*x^(N-1) + ... + P(N)*x + P(N+1)x=1:10;y= polyval([3 2],x)y =5 8 11 14 17 20 23 26 29 32[3 2]有两个数，因此为一次多项式，即y=3x+2如：x=1:10;y=[193 226 240 244 257 260 274 297 350 420];p=polyfit(x,3)y1= polyval(p,x)norm(y-y1)ans =8.0464如果是矩阵，则polyval(p,x)为对应x的每一个预测值。
第六章MATLAB数据分析与功能函数
第六章MATLAB数据分析与功能函数在MATLAB中，有很多强大的数据分析和功能函数，可以帮助我们对数据进行处理、分析和可视化。
本章将介绍一些常用的数据分析和功能函数，并使用实例来介绍它们的用法。
1.统计函数MATLAB提供了丰富的统计函数，可以进行各种统计计算，例如平均值、标准差、中位数等。
- mean函数用于计算数组的平均值，例如：mean([1, 2, 3])的结果是2- std函数用于计算数组的标准差，例如：std([1, 2, 3])的结果是0.8165- median函数用于计算数组的中位数，例如：median([1, 2, 3])的结果是22.数据拟合函数MATLAB提供了拟合函数，可以用来对数据进行曲线拟合，从而得到数据的数学模型。
- polyfit函数用于进行多项式拟合，例如：x = [1, 2, 3, 4, 5]; y = [1, 4, 9, 16, 25]; p = polyfit(x, y, 2);表示对数据点进行二次多项式拟合，并返回拟合的系数。
3.数据聚类函数MATLAB提供了强大的数据聚类函数，可以将数据集分成多个不同的类别。
- kmeans函数用于进行k-means聚类，例如：x = [1, 1.5, 3, 3.5, 4, 6]; idx = kmeans(x, 2);表示对数据进行2类聚类，并返回每个数据点所属的类别。
- gmdistribution函数用于进行高斯混合模型聚类，例如：x = [1, 1.5, 3, 3.5, 4, 6]; gm = gmdistribution.fit(x', 2);表示对数据进行高斯混合模型聚类，并返回聚类结果。
4.数据可视化函数MATLAB提供了各种数据可视化函数，可以将数据以图表的形式展示出来，便于数据分析和理解。
- plot函数用于绘制折线图，例如：x = [1, 2, 3, 4, 5]; y = [1, 4, 9, 16, 25]; plot(x, y);表示将x和y的数据点用折线连接起来。
最新第6章 MATLAB数据分析与多项式计算_习题答案
精品好文档，推荐学习交流第6章 MATLAB数据分析与多项式计算习题6一、选择题1．设A=[1,2,3,4,5;3,4,5,6,7]，则min(max(A))的值是（）。
BA．1 B．3 C．5 D．72．已知a为3×3矩阵，则运行mean(a)命令是（）。
BA．计算a每行的平均值B．计算a每列的平均值C．a增加一行平均值D．a增加一列平均值3．在MA TLAB命令行窗口输入下列命令：>> x=[1,2,3,4];>> y=polyval(x,1);则y的值为（）。
DA．5 B．8 C．24 D．104．设P是多项式系数向量，A为方阵，则函数polyval(P,A)与函数polyvalm(P,A)的值（）。
DA．一个是标量，一个是方阵B．都是标量C．值相等D．值不相等5．在MA TLAB命令行窗口输入下列命令：>> A=[1,0,-2];>> x=roots(A);则x(1)的值为（）。
CA．1 B．-2 C．1.4142 D．-1.41426．关于数据插值与曲线拟合，下列说法不正确的是（）。
AA．3次样条方法的插值结果肯定比线性插值方法精度高。
B．插值函数是必须满足原始数据点坐标，而拟合函数则是整体最接近原始数据点，而不一定要必须经过原始数据点。
C．曲线拟合常常采用最小二乘原理，即要求拟合函数与原始数据的均方误差达到极小。
D．插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题1．设A=[1,2,3;10 20 30;4 5 6]，则sum(A)= ，median(A)= 。
[15 27 39]，[4 5 6[2．向量[2,0,-1]所代表的多项式是。
2x2-1仅供学习与交流，如有侵权请联系网站删除谢谢1精品好文档，推荐学习交流3．为了求ax2+bx+c=0的根，相应的命令是（假定a、b、c已经赋值）。
为了将求得的根代回方程进行验证，相应的命令是。
第6章 MATLAB数据分析与多项式计算
3．两个向量或矩阵对应元素的比较 ． U=max(A,B) A,B是两个同型的向量或矩阵，结果 是与 是两个同型的向量或矩阵， 是两个同型的向量或矩阵 结果U是与 A,B同型的向量或矩阵，U的每个元素等于 同型的向量或矩阵， 的每个元素等于 的每个元素等于A,B 同型的向量或矩阵 对应元素的较大者。 对应元素的较大者。 (2) U=max(A,n) n是一个标量，结果 是与 同型的向量或 是一个标量， 是与A同型的向量或 是一个标量 结果U是与 矩阵， 的每个元素等于 对应元素和n中的较 的每个元素等于A对应元素和 矩阵，U的每个元素等于 对应元素和 中的较 大者。 大者。 min函数的用法和 函数的用法和max完全相同。 完全相同。 函数的用法和 完全相同 求两个2× 矩阵 矩阵x, 所有同一位置上的较大 例6-3 求两个 ×3矩阵 y所有同一位置上的较大 元素构成的新矩阵p。 元素构成的新矩阵 。
6.1.3 平均值和中值 mean(X) 返回向量X的算术平均值 的算术平均值。 返回向量 的算术平均值。 median(X) 返回向量 的中值。 返回向量X的中值 的中值。 mean(A) 返回一个行向量，其第i个元素是 的第i列 个元素是A的第 返回一个行向量，其第 个元素是 的第 列 的算术平均值。 的算术平均值。 median(A) 返回一个行向量，其第 个元素是 的第 返回一个行向量，其第i个元素是 的第i 个元素是A的第 列的中值。 列的中值。 mean(A,dim) 当dim为1时，该函数等同于 为 时 该函数等同于mean(A)；当 ； dim为2时，返回一个列向量，其第 个元素是 的第 个元素是A的第 为 时 返回一个列向量，其第i个元素是 的第i 行的算术平均值。 行的算术平均值。 median(A,dim) 当dim为1时，该函数等同于 为 时 该函数等同于median(A)； ； 个元素是A的 当dim为2时，返回一个列向量，其第 个元素是 的 为 时 返回一个列向量，其第i个元素是 行的中值。 第i行的中值。 行的中值 分别求向量x与 的平均值和中值 的平均值和中值。 例6-5 分别求向量 与y的平均值和中值。
第6章MATLAB数据分析与多项式计算
第6章MATLAB数据分析与多项式计算MATLAB是一种面向科学和工程计算的计算机语言和环境。
它具有强大的数据分析和多项式计算功能，可以用于数据处理、统计分析、曲线拟合、插值计算、解方程等多种应用。
数据分析是从数据中提取有用信息的过程，其中使用MATLAB可以轻松地进行各种数据操作和分析。
MATLAB提供了各种统计分析函数，可以计算数据的统计特征，如均值、方差、标准差、相关系数等。
同时，它还提供了数据绘图功能，可以将数据以直方图、散点图、折线图等形式展示出来，帮助用户更好地理解数据。
多项式计算是利用多项式进行数值计算的过程。
在MATLAB中，可以使用多种方法进行多项式计算，如多项式加减乘除、多项式求值、多项式插值等。
MATLAB提供了丰富的多项式操作函数，可以方便地进行多项式运算和计算。
在数据分析中，多项式计算经常用于曲线拟合和插值计算。
曲线拟合是根据给定的数据点，找出一个与之最接近的曲线。
MATLAB提供了polyfit函数，可以根据给定的数据点和多项式阶数，自动拟合出最优的多项式曲线。
此外，MATLAB还提供了curvefit函数，可以进行更加复杂的曲线拟合，如指数曲线拟合、对数曲线拟合等。
插值计算是根据已知的数据点，通过插值方法找出在这些数据点之间的未知点的近似值。
MATLAB提供了interp1函数，可以根据给定的数据点和插值方法，自动进行插值计算。
此外，MATLAB还提供了interp2函数，可以进行二维插值计算。
除了数据分析和多项式计算功能，MATLAB还具有其他强大的数值计算功能，如数值积分、数值微分、解线性方程组等。
这些功能使得MATLAB成为科学与工程领域中常用的计算工具。
在使用MATLAB进行数据分析和多项式计算时，需要注意数据的有效性和合理性。
数据分析的结果只能作为参考，不能作为绝对的判断依据。
多项式计算的结果也可能存在误差，需要进行适当的精度控制。
总之，MATLAB是一款功能强大的数据分析和多项式计算工具，可以帮助科学家和工程师快速、准确地进行各种数值计算和分析任务。
第6章 MATLAB数据分析与多项式计算_习题答案教学提纲
第6章M A T L A B数据分析与多项式计算_习题答案精品资料第6章 MATLAB数据分析与多项式计算习题6一、选择题1．设A=[1,2,3,4,5;3,4,5,6,7]，则min(max(A))的值是（）。
BA．1 B．3 C．5 D．72．已知a为3×3矩阵，则运行mean(a)命令是（）。
BA．计算a每行的平均值 B．计算a每列的平均值C．a增加一行平均值 D．a增加一列平均值3．在MATLAB命令行窗口输入下列命令：>> x=[1,2,3,4];>> y=polyval(x,1);则y的值为（）。
DA．5 B．8 C．24 D．104．设P是多项式系数向量，A为方阵，则函数polyval(P,A)与函数polyvalm(P,A)的值（）。
DA．一个是标量，一个是方阵 B．都是标量C．值相等 D．值不相等5．在MATLAB命令行窗口输入下列命令：>> A=[1,0,-2];>> x=roots(A);则x(1)的值为（）。
CA．1 B．-2 C．1.4142 D．-1.41426．关于数据插值与曲线拟合，下列说法不正确的是（）。
AA．3次样条方法的插值结果肯定比线性插值方法精度高。
B．插值函数是必须满足原始数据点坐标，而拟合函数则是整体最接近原始数据点，而不一定要必须经过原始数据点。
C．曲线拟合常常采用最小二乘原理，即要求拟合函数与原始数据的均方误差达到极小。
D．插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题1．设A=[1,2,3;10 20 30;4 5 6]，则sum(A)= ，median(A)= 。
[15 27 39]，[4 5 6[2．向量[2,0,-1]所代表的多项式是。
2x2-1仅供学习与交流，如有侵权请联系网站删除谢谢2精品资料3．为了求ax2+bx+c=0的根，相应的命令是（假定a、b、c已经赋值）。
matlab课后习题答案1到6章
欢迎共阅习题二1.如何理解“矩阵是MATLAB 最基本的数据对象”？ 答：因为向量可以看成是仅有一行或一列的矩阵，单个数据（标量）可以看成是仅含一个元素的矩阵，故向量和单个数据都可以作为矩阵的特例来处理。
(2) 删除矩阵A 的第7号元素。
答：A(7)=[](3) 将矩阵A 的每个元素值加30。
答：A=A+30;(4) 求矩阵A 的大小和维数。
答：size(A);ndims(A);(5) 将向量 t 的0元素用机器零来代替。
答：t(find(t==0))=eps; (6) 将含有12个元素的向量 x 转换成34⨯矩阵。
答：reshape(x,3,4); (7) 求一个字符串的ASCII码。
答：abs(‘123’); 或E 。
答：B=A(1:3,:); C=A(:,1:2); D=A(2:4,3:4);E=B*C;(2) 分别求E<D 、E&D 、E|D 、~E|~D 和find(A>=10&A<25)。
答：E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，11⎡⎤⎢⎥答：student(1).id='0001';student(1).name='Tom'; student(1).major='computer';student(1).grade=[89,78,67,90,86,85]; 8.建立单元矩阵B 并回答有关问题。
B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3); B{2,2}={12,34,2;54,21,3;4 ,23,67};(1)size(B)和ndims(B)的值分别是多少？答：size(B) 的值为2, 2。
ndims(B) 的值为2。
(2)B(2)和B(4)的值分别是(2)建立5×6随机矩阵A，其元素为[100,200]范围内的随机整数。
第6章_MATLAB数值计算_part2
6.2.2 数值积分
b a b
f ( x)dx p1 ( x)dx (b a )
a
b
f (a ) f (b) 2 ab
( f (a) 4 f ( ) f (b)) 数值积分方法 6 2 n 1 求解定积分的数值方法多种多样， h T f ( a ) f ( b ) 2 f ( a kh ) n 如简单的梯形法、辛普生 2 k 1 (Simpson)• 法、牛顿－柯特斯 h S ( f (x ) 4 f (x ) f ( x 1)) (Newton-Cotes)法等都是经常采 6 用的方法。 h f (a) 4 f ( x ) 2 f ( x ) f (b) 基本思想 6
第6章 MATLAB数值计算
6.1 6.2 6.3 6.4 6.5 数据处理与多项式计算 数值微积分 线性方程组求解 最优化问.1 数值微分（导数） 不关心微分的形式和性质，只关心该微分在一串离散点 的近似值以及所计算的近似值有多大的误差。 MATLAB下求数值导数的两种方法：
I e
0
1
x2
dx
2 被积函数由一个表格定义
在科学实验和工程应用中，函数关系往往是不知道 的，只有实验测定的一组样本点和样本值，这时， 就无法使用quad函数计算其定积分。 在MATLAB中，对由表格形式定义的函数关系的求 定积分问题用trapz(X,Y)函数。 其中向量X、Y定义函数关系Y=f(X)。
值得一提的是，当已知给出的样本数N0不是2 的幂次时，可以取一个N使它大于N0且是2 的幂次，然后利用函数格式fft(X,N)或 fft(X,N,dim)便可进行快速傅立叶变换。这 样，计算速度将大大加快。 相应地，一维离散傅立叶逆变换函数是ifft。 ifft(F)返回F的一维离散傅立叶逆变换； ifft(F,N)为N点逆变换；ifft(F,[],dim)或 ifft(F,N,dim)则由N或dim确定逆变换的点数 或操作方向。
第六章MATLAB数据分析与功能函数
A=
8
1
6
3
5
7
4
9
2
>> [Y,I]=sort(A,2,'descend') Y=
861 753 942 I= 132 321 213
10 点击图形窗口的Tool\Data Statistics，对数据进行分析
6.1.2 用于场论的数据分析函数
1.两个向量点积运算dot 2. 两个向量叉积运算cross
7. 求积与累乘积 (和前面所有的数相乘放在现在的位置)
prod(X)：返回向量X各元素的乘积。 prod(A)：返回一个行向量，其第i个元素是A的第i列的元素乘积。 prod(A,dim)：当dim为1时，该函数等同于prod(A)；当dim为2时，返回一个 列向量，其第i个元素是A的第i行的各元素乘积。 cumprod(X)：返回向量X累乘积向量。 cumprod(A)：返回一个矩阵，其第i列是A的第i列的累乘积向量。 cumprod(A,dim)：当dim为1时，该函数等同于cumprod(A)；当dim为2时， 返回一个向量，其第i行是A的第i行的累乘积向量。
数据序列求和与求积的函数是sum和prod，其使用方法类似。设X是 一个向量，A是一个矩阵，函数的调用格式为： sum(X)：返回向量X各元素的和。 sum(A)：返回一个行向量，其第i个元素是A第i列的元素和。 sum(A,dim)：当dim为1时，该函数等同于sum(A)；当dim为2时，返回一 个列向量，其第i个元素是A的第i行的各元素之和。 cumsum(X)：返回向量X累加和向量。 cumsum(A)：返回一个矩阵，其第i列是A的第i列的累加和向量。 cumsum(A,dim)：当dim为1时，该函数等同于cumsum(A)；当dim为2时 ，返回一个矩阵，其第i行是A的第i行的累加和向量。
matlab习题6答案
matlab习题6答案Matlab习题6答案Matlab是一种广泛应用于科学计算和工程领域的高级编程语言和环境。
它以其强大的数值计算和数据可视化功能而闻名于世。
在Matlab的学习过程中，习题是提高编程技能和理解语言特性的重要方式。
在本文中，我将为大家提供Matlab习题6的答案，帮助大家更好地理解和掌握Matlab编程。
习题1：编写一个Matlab函数，计算给定向量的均值和标准差。
函数的输入参数为一个向量，输出为该向量的均值和标准差。
解答：```matlabfunction [mean_value, std_value] = calculate_stats(vector)mean_value = mean(vector);std_value = std(vector);end```习题2：编写一个Matlab函数，计算给定矩阵的特征值和特征向量。
函数的输入参数为一个矩阵，输出为该矩阵的特征值和特征向量。
解答：```matlabfunction [eigenvalues, eigenvectors] = calculate_eigen(matrix)[eigenvectors, eigenvalues] = eig(matrix);end```习题3：编写一个Matlab函数，计算给定矩阵的逆矩阵。
函数的输入参数为一个矩阵，输出为该矩阵的逆矩阵。
解答：```matlabfunction inverse_matrix = calculate_inverse(matrix)inverse_matrix = inv(matrix);end```习题4：编写一个Matlab函数，实现矩阵的转置操作。
函数的输入参数为一个矩阵，输出为该矩阵的转置矩阵。
解答：```matlabfunction transpose_matrix = calculate_transpose(matrix)transpose_matrix = matrix';end```习题5：编写一个Matlab函数，计算给定向量的累积和。
第6章 MATLAB数据分析与多项式计算_习题答案
第6章 MATLAB数据分析与多项式计算习题6一、选择题1．设A=[1,2,3,4,5;3,4,5,6,7]，则min(max(A))的值是（）。
BA．1 B．3 C．5 D．72．已知a为3×3矩阵，则运行mean(a)命令是（）。
BA．计算a每行的平均值B．计算a每列的平均值C．a增加一行平均值D．a增加一列平均值3．在MA TLAB命令行窗口输入下列命令：>> x=[1,2,3,4];>> y=polyval(x,1);则y的值为（）。
DA．5 B．8 C．24 D．104．设P是多项式系数向量，A为方阵，则函数polyval(P,A)与函数polyvalm(P,A)的值（）。
DA．一个是标量，一个是方阵B．都是标量C．值相等D．值不相等5．在MA TLAB命令行窗口输入下列命令：>> A=[1,0,-2];>> x=roots(A);则x(1)的值为（）。
CA．1 B．-2 C．1.4142 D．-1.41426．关于数据插值与曲线拟合，下列说法不正确的是（）。
AA．3次样条方法的插值结果肯定比线性插值方法精度高。
B．插值函数是必须满足原始数据点坐标，而拟合函数则是整体最接近原始数据点，而不一定要必须经过原始数据点。
C．曲线拟合常常采用最小二乘原理，即要求拟合函数与原始数据的均方误差达到极小。
D．插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题1．设A=[1,2,3;10 20 30;4 5 6]，则sum(A)= ，median(A)= 。
[15 27 39]，[4 5 6[2．向量[2,0,-1]所代表的多项式是。
2x2-13．为了求ax2+bx+c=0的根，相应的命令是（假定a、b、c已经赋值）。
为了将求得的根代回方程进行验证，相应的命令是。
x=roots([a,b,c])，polyval([a,b,c],x)4．如果被插值函数是一个单变量函数，则称为插值，相应的MA TLAB函数是。
MATLAB编程与工程应用——第6章 MATLAB数据分析与多项式计算
MATLAB数据分析与多项式计算
二、二维数据插值
某实验对一根长10 10米的钢轨进行热源的温度传播测 例6.10 某实验对一根长10米的钢轨进行热源的温度传播测 表示测量点0:2.5:10( 0:2.5:10(米 试。用x表示测量点0:2.5:10(米)，用h表示测量时间 0:30:60(秒 表示测试所得各点的温度(℃) (℃)。 0:30:60(秒)，用T表示测试所得各点的温度(℃)。试用 线性插值求出在一分钟内每隔20 20秒 钢轨每隔1 线性插值求出在一分钟内每隔20秒、钢轨每隔1米处的温 TI。 度TI。 命令如下： x=0:2.5:10; h=[0:30:60]'; T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; xi=[0:10]; hi=[0:20:60]'; TI=interp2(x,h,T,xi,hi) exp6_10.m
MATLAB数据分析与多项式计算
6.2 数据插值
二、二维数据插值
z1=interp2(x,y,z,x1,y1,'method') 其中x,y是两个向量，分别描述两个参数的采样点， z是与参数采样点对应的函数值， x1,y1是两个向量或标量，描述欲插值的点。 z1是根据相应的插值方法得到的插值结果。 method的取值与一维插值函数相同。 x,y,z也可以是矩阵形式。 x1,y1的取值范围不能超出x,y的给定范围，否则，会给 出“NaN”错误。
MATLAB数据分析与多项式计算
MATLAB数据分析与多项式计算
一、最大值和最小值
格式3 3. 格式3 U=max(x,y) U=min(x,y) 如果x为标量，则y可为标量、向量或矩阵 如果x为向量或矩阵，则y可为标量或与x同维的向量或 矩阵 x,y是两个同型的向量或矩阵，结果U是与x,y同型的向 量或矩阵，U的每个元素等于x,y对应元素的较大/小者。 如果y是一个标量，结果U是与x同型的向量或矩阵，U 的每个元素等于x对应元素和y中的较大/小者。 例6.3 求两个2×3矩阵x, y所有同一位置上的较大元素 求两个2 矩阵x, y所有同一位置上的较大元素 构成的新矩阵p 构成的新矩阵p。exp6_3.m
第6章 MATLAB数值计算_part2
k =0
k +1/ 2
k =1
k
公式： 公式：
数值积分的实现
1.被积函数是一个解析式 被积函数是一个解析式
quad(filename,a,b,tol,trace) quadl(filename,a,b,tol,trace)
filename:被积函数名；a, b积分区间 被积函数名； 被积函数名 积分区间 tol：积分精度；trace：控制是否展现积分过程 ：积分精度； ：
DX=diff(X)：计算向量X的向前差分，DX(i)=X(i+1)-X(i)， ：计算向量 的向前差分 的向前差分， ， i=1,2,…,n-1。 。 DX=diff(X,n)：计算 的n阶向前差分。例如， 阶向前差分。 ：计算X的 阶向前差分 例如， diff(X,2)=diff(diff(X))。 。 DX=diff(A,n,dim)：计算矩阵 的n阶差分，dim=1时(缺省状态 ， 阶差分， 缺省状态)， ：计算矩阵A的 阶差分 时 缺省状态 计算差分； 计算差分。 按列计算差分；dim=2，按行计算差分。 ，
(1) 建立一个函数文件 建立一个函数文件fxy.m： ： function f=fxy(x,y) global ki; ki=ki+1; %ki用于统计被积函数的调用次数 用于统计被积函数的调用次数 f=exp(-x.^2/2).*sin(x.^2+y); (2) 调用dblquad函数求解。 调用dblquad函数求解 函数求解。 global ki;ki=0; I=dblquad('fxy',-2,2,-1,1) ki I= 1.57449318974494 ki = 1038
X、Y是两个等长的向量：X=(x1,x2,…,xn)， 、 是两个等长的向量 是两个等长的向量： ， Y=(y1,y2,…,yn)， ， x1<x2<…<xn 积分区间是[x1， 。 积分区间是 ，xn]。
第6章MATLAB数据分析与多项式计算_习题答案
第6章MATLAB数据分析与多项式计算习题6一、选择题1．设A=[1,2,3,4,5;3,4,5,6,7]，则min(max(A))的值是（）。
BA．1B．3C．5D．72．已知a为3×3矩阵，则运行mean(a)命令是（）。
BA．计算a每行的平均值B．计算a每列的平均值C．a增加一行平均值D．a增加一列平均值3．在MATLAB命令行窗口输入下列命令：>>x=[1,2,3,4];>>y=polyval(x,1);则y的值为（）。
DA．5B．8C．24D．104．设P是多项式系数向量，A为方阵，则函数polyval(P,A)与函数polyvalm(P,A)的值（）。
DA．一个是标量，一个是方阵B．都是标量C．值相等D．值不相等5．在MATLAB命令行窗口输入下列命令：>>A=[1,0,-2];>>x=roots(A);则x(1)的值为（）。
CA．1B．-2C．1.4142D．-1.41426．关于数据插值与曲线拟合，下列说法不正确的是（）。
AA．3次样条方法的插值结果肯定比线性插值方法精度高。
B．插值函数是必须满足原始数据点坐标，而拟合函数则是整体最接近原始数据点，而不一定要必须经过原始数据点。
C．曲线拟合常常采用最小二乘原理，即要求拟合函数与原始数据的均方误差达到极小。
D．插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题1．设A=[1,2,3;102030;456]，则sum(A)=，median(A)=。
[152739]，[456[2．向量[2,0,-1]所代表的多项式是。
2x 2-123．为了求a x +b x +c =0的根，相应的命令是（假定a 、b 、c 值）。
为了 将求得的根代回方程进行验证，相应的命令是。
x=roots([a,b,c])，polyval([a,b,c],x)4．如果被插值函数是一个单变量函插值，相应的MATLAB 函数 是。
MATLAB课件--第六章：数据分析与多项式计算
第六章 MATLAB数据分析 数据分析 与多项式计算 6.1 数据统计处理 6.2 插值 6.3 曲线拟合 6.4 多项式计算
6.1 数据统计处理
6.1.1 最大值和最小值
MATLAB提供的求数据序列的最大值和最小值的函数 MATLAB提供的求数据序列的最大值和最小值的函数 分别为max min， max和 分别为max和min，两个函数的调用格式和操作过程 类似。 类似。
费马 目录 上页 下页 返回 结束
3．两个向量或矩阵对应元素的比较 ．
函数max和min还能对两个同型的向量或矩阵进行比 和 函数 还能对两个同型的向量或矩阵进行比 调用格式为： 较，调用格式为： 是两个同型的向量或矩阵， (1) U=max(A,B)：A,B是两个同型的向量或矩阵， ：A,B是两个同型的向量或矩阵 结果U是与A,B同型的向量或矩阵， A,B同型的向量或矩阵 结果U是与A,B同型的向量或矩阵，U的每个元素等 A,B对应元素的较大者 对应元素的较大者。 于A,B对应元素的较大者。 (2) U=max(A,n)：n是一个标量，结果 是与 同型的 是一个标量， 是与A同型的 ： 是一个标量 结果U是与 向量或矩阵， 的每个元素等于 对应元素和n中的 的每个元素等于A对应元素和 向量或矩阵，U的每个元素等于 对应元素和 中的 较大者。 较大者。 min函数的用法和 函数的用法和max完全相同。 完全相同。 函数的用法和 完全相同
费马
目录
上页
下页
返回
结束
mean(A,dim)：当dim为1时，该函数等同于 ： 为 时 mean(A)；当dim为2时，返回一个列向量，其 ； 为 时 返回一个列向量， 个元素是A的第 行的算术平均值。 第i个元素是 的第 行的算术平均值。 个元素是 的第i行的算术平均值 median(A,dim)：当dim为1时，该函数等同于 ： 为 时 median(A)；当dim为2时，返回一个列向量， ； 为 时 返回一个列向量， 其第i个元素是 的第i行的中值 个元素是A的第 行的中值。 其第 个元素是 的第 行的中值。
6.1 数据统计处理
6.1.1 最大值和最小值
MATLAB提供的求数据序列的最大值和最小值的函数 MATLAB提供的求数据序列的最大值和最小值的函数 分别为max min， max和 分别为max和min，两个函数的调用格式和操作过程 类似。 类似。
费马 目录 上页 下页 返回 结束
3．两个向量或矩阵对应元素的比较 ．
函数max和min还能对两个同型的向量或矩阵进行比 和 函数 还能对两个同型的向量或矩阵进行比 调用格式为： 较，调用格式为： 是两个同型的向量或矩阵， (1) U=max(A,B)：A,B是两个同型的向量或矩阵， ：A,B是两个同型的向量或矩阵 结果U是与A,B同型的向量或矩阵， A,B同型的向量或矩阵 结果U是与A,B同型的向量或矩阵，U的每个元素等 A,B对应元素的较大者 对应元素的较大者。 于A,B对应元素的较大者。 (2) U=max(A,n)：n是一个标量，结果 是与 同型的 是一个标量， 是与A同型的 ： 是一个标量 结果U是与 向量或矩阵， 的每个元素等于 对应元素和n中的 的每个元素等于A对应元素和 向量或矩阵，U的每个元素等于 对应元素和 中的 较大者。 较大者。 min函数的用法和 函数的用法和max完全相同。 完全相同。 函数的用法和 完全相同
费马
目录
上页
下页
返回
结束
mean(A,dim)：当dim为1时，该函数等同于 ： 为 时 mean(A)；当dim为2时，返回一个列向量，其 ； 为 时 返回一个列向量， 个元素是A的第 行的算术平均值。 第i个元素是 的第 行的算术平均值。 个元素是 的第i行的算术平均值 median(A,dim)：当dim为1时，该函数等同于 ： 为 时 median(A)；当dim为2时，返回一个列向量， ； 为 时 返回一个列向量， 其第i个元素是 的第i行的中值 个元素是A的第 行的中值。 其第 个元素是 的第 行的中值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第6章 MATLAB数据分析与多项式计算
习题6
一、选择题
1．设A=[1,2,3,4,5;3,4,5,6,7]，则min(max(A))的值是（）。
B A．1 B．3 C．5 D．7
2．已知a为3×3矩阵，则运行mean(a)命令是（）。
B
A．计算a每行的平均值 B．计算a每列的平均值
C．a增加一行平均值 D．a增加一列平均值
3．在MATLAB命令行窗口输入下列命令：
>> x=[1,2,3,4];
>> y=polyval(x,1);
则y的值为（）。
D
A．5 B．8 C．24 D．10
4．设P是多项式系数向量，A为方阵，则函数polyval(P,A)与函数polyvalm(P,A)的值（）。
D
A．一个是标量，一个是方阵 B．都是标量
C．值相等 D．值不相等
5．在MATLAB命令行窗口输入下列命令：
>> A=[1,0,-2];
>> x=roots(A);
则x(1)的值为（）。
C
A．1 B．-2 C． D．
6．关于数据插值与曲线拟合，下列说法不正确的是（）。
A
A．3次样条方法的插值结果肯定比线性插值方法精度高。
B．插值函数是必须满足原始数据点坐标，而拟合函数则是整体最接近原始数据点，而不一定要必须经过原始数据点。
C．曲线拟合常常采用最小二乘原理，即要求拟合函数与原始数据的均方误差达到极小。
D．插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题
1．设A=[1,2,3;10 20 30;4 5 6]，则sum(A)= ，median(A)= 。
[15 27 39]，[4 5 6[
2．向量[2,0,-1]所代表的多项式是。
2x2-1
3．为了求ax2+bx+c=0的根，相应的命令是（假定a、b、c已经赋值）。
为了
将求得的根代回方程进行验证，相应的命令是。
x=roots([a,b,c])，polyval([a,b,c],x)
4．如果被插值函数是一个单变量函数，则称为插值，相应的MATLAB函数是。
一维，interp1
5．求曲线拟合多项式系数的函数是，计算多项式在给定点上函数值的函数是。
polyfit，polyval
三、应用题
1．利用MATLAB提供的randn函数生成符合正态分布的10×5随机矩阵A，进行如下操作：
（1）A各列元素的均值和标准方差。
（2）A的最大元素和最小元素。
（3）求A每行元素的和以及全部元素之和。
（4）分别对A的每列元素按升序、每行元素按降序排序。
第一题:
(1):
A=randn(10,5)
B=mean(A)
C=std(A)
(2):
mx=max(max(A))
mn=min(min(A))
(3):
sm=sum(A,2)
sz=sum(sum(A))
(4):
[Y,I]=sort(A,1)
[Z,J]=sort(A,2)；
rot90(Z,1)'%旋转90度后，再转置便可得到每行按降序排列
2．已知多项式P1(x)=3x+2，P2(x)=5x2-x+2，P3(x)=，求：
（1）P(x)=P1(x) P2(x)P3(x)。
（2）P(x)=0的全部根。
（3）计算x i=(i=0，1，2，…，10)各点上的P(x i)。
第二题：
(1):
p1=[0,3,2];
p2=[5,-1,2];
p3=[1,0,];
p=conv(conv(p1,p2),p3)%先将p1与p2乘，再与p3乘，conv函数只能有两个
(2):
x=roots(p)
(3):
a=0:10;
b=*a;
y=polyval(p,b)
3．按表6-4用3次样条方法插值计算0~90º内整数点的正弦值和0~75º内整数点的正切值，然后用5次多项式拟合方法计算相同的函数值，并将两种计算结果进行比较。
表6-4 特殊角的正弦与正切值表
第三题：
(1):
sin(x)函数：
三次样条方法：
x=0:90;
a=[0,15,30,45,60,75,90];
f=[0,,,,,,1];
interp1(a,f,x,'spline')%spline要加单引号，否则错误；还可以用spline(a,f,x)函数
5次多项式拟合方法：
x=0:90;
a=[0,15,30,45,60,75,90];
f=[0,,,,,,1];
q=polyfit(a,f,5);
y=polyval(q,x);
plot(x,p,':o',x,y,'-*')
tan(x)函数：
三次样条方法：
x=0:75;
a=[0,15,30,45,60,75];
f=[0,,,1,,];
interp1(a,f,x,'spline')%spline要加单引号，否则错误
5次多项式拟合方法：
x=0:75;
a=[0,15,30,45,60,75];
f=[0,,,1,,];
p=polyfit(a,f,5);
y=polyval(p,x);
plot(x,ans,':o',x,y,'-*')
4．已知一组实验数据如表6-5所示。
表6-5 一组实验数据
求它的线性拟合曲线。
第三题：
x=[165,123,150,123,141];
y=[187,126,172,125,148];
p=polyfit(x,y,1);
q=polyval(p,x);
plot(x,q)。