当前位置：文档之家 › 方波信号f(t)展开为傅里叶级数.ppt

方波信号f(t)展开为傅里叶级数.ppt

  • 格式：ppt
  • 大小：1.60 MB
  • 文档页数：84

下载文档原格式

  / 84

合集下载

方波信号的傅里叶变换

方波信号的傅里叶变换

例4―3 求矩形脉冲信号gτ(t)的频谱。
g (t) F()
1
－ 2/
2/
－/ 2 0 / 2
(a)
t
0 (b )

图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
1 g r (t ) 0 gτ(t)的傅里叶变换为 t t
f (t ) 1

t
F ( j ) 1 e jt dt
单位直流信号的频谱
例4―6 求单位直流信号的频谱。 解 幅度为1的单位直流信号可表示为 f(t)=1,-∞<t<∞ (4―44) 它可以看作是双边指数信号在α取极限趋近0时的一个 特例,即
1 lim e
0
t
u (t ), 0 u( t )] lim[ e
0
t
(4―45)
[1] [lim e
0
t
2a u( t )] lim 2 0 a 2
(4―46)
0 0 0
lim

0
2 2 d lim d( ) 2 2 0 1 ( )2
(4―50)
f (t)
F()
1
0 －1 (a )
t
0

(b )
图4.10 符号函数及其频谱
符号函数sgn(t)也可看作是下述函数在α取极限趋近0时的一 个特例: t e t0 (其中α>0) f ( t ) t t0 e
F [ f (t )]
F(j ) 1
f (t )
积分变换第1讲----傅里叶(Fourier)级数展开

积分变换第1讲----傅里叶(Fourier)级数展开

方波
4个正弦波的逼近
100个正弦波的逼近
5
研究周期函数实际上只须研究其中的一个周期内
的情况即可, 通常研究在闭区间[-T/2,T/2]内函
数变化的情况. 并非理论上的所有周期函数都可 以用傅里叶级数逼近, 而是要满足狄利克雷
(Dirichlet)条件, 即在区间[-T/2,T/2]上
1, 连续或只有有限个第一类间断点 2, 只有有限个极值点 这两个条件实际上就是要保证函数是可积函
cn
=
1 8
sinc( wn )
(n
=
0,1,2,)
wn
=
nw
=
n 2p
16
=
np
8
, 再将cn以竖线标在频率图上
w
32
一般地, 对于周期T
cn
=
1 T
T
2 -T
fT (t)e- jwnt dt
2
= 1 1 e- jwnt dt
T -1
1
= 1 e- jwnt
= 1 e jwn - e- jwn
mwt cos nwt d t
=
m=1
2
= an
T
2 cos2 nwt d t
-T 2
=
an
T 2
即
an
=
2 T
T 2 -T 2
fT (t) cos nwt d t
16
同理, 为求bn, 计算[fT(t), sin nwt], 即
T 2 -T 2
fT (t) sin nwt d t =
T 2
T
2 -T
fT (t)e- jnwt d t
2
21
而
方波信号的傅里叶变换_图文

方波信号的傅里叶变换_图文


(4―45)
(4―46)
(4―47)
(4―48) (4―49)
图4.9 单位直流信号及其频谱
符号函数Sgn(t)的频谱函数
例 3.4-7 求符号函数Sgn(t)的频谱函数。
考察例 3.4-4 所示信号f(t)
当α→0时，其极限为符号函数Sgn(t)。因而可以用求f(t)的频 谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
图 3.8-2 例 3.8-2 (a) 系统组成； (b) s(t)的波形
先求f(t)的傅里叶变换F(jω)，由于
再求s(t)的傅里叶变换S(jω)。由于s(t)为周期信号，T=1ms，则 , 因而有
图 3.8-3 y(t)的求解
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
解 图示信号f(t)可表示为
(a>0)
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
Байду номын сангаас
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
gτ(t)的傅里叶变换为
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
傅里叶变化例题

傅里叶变化例题


2 T
0 T
2
(1)sin(2 nft)dt 2
T
T 2 0
1 sin(2 nft)dt
2 T
1
2 nft
[ cos(2 nft)]
0 T
2
2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
4
n
n 2, 4,6, n 1,3,5,
c 2 T
T
2 T
2
试画出f(t)的振幅谱和相位谱。 解 f(t)为周期信号，题中所给的f(t)表达式可视为f(t)的傅里叶级数展开式。据
f
(t)
A0 2
n1
An cos(nt
n )
可知，其基波频率Ω=π(rad/s)，基本周期T=2 s，ω=2π、3π、 6 π分别为二、 三、六 次谐波频率。且有
A0 1 2 A1 3
jt dt
1
可见，冲激函数δ(t)的频谱是常数1。也就是说，δ(t)中包含了所有的频率分量， 而各频率分量的频谱密度都相等。 显然， 信号δ(t)实际上是无法实现的。
f (t) 1 1e jtd
2
根据分配函数关于δ(t)的定义， 有
冲激信号Δ(T)的频谱
例4―2求冲激信号δ(t)的频谱。 解 由频谱函数的定义式有
例 3.4-4 所示信号的频谱函数为
，从而有
2 j2 2
Sg n(t)
X( )
1
o
t
o
－1
(a) (b)
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形； (b) 频谱
符号函数的频谱
例4―7求符号函数的频谱。 解 符号函数简记为sgn(t),它的定义为
方波信号f展开为傅里叶级数

方波信号f展开为傅里叶级数

2
f (t)sin(2nft)dt
2
T
0 T
2
(1)sin(2nft)dt 2
T
T 2 0
1 sin(2nft)dt

2 T
1 [cos(2nft)] 2 nft
0 T
2

2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,


2

－4
－
2
o
4

(b )
F( )
( )

－4 －2 o
2 4


－4 －2
o 2 4

－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
15 °
10 °
o

2
3
4 5
6

(b )
图 3.3-1 例 3.3-1
(a) 振幅谱； (b) (b) 相位谱
|F n |
2
1 .5
1 .5
1
1
1

0 .4 0 .2
0 .4 0 .2
－ 6－ 5 － 4－ 3－ 2 － o
2 3 4 5 6
(a )
n 45°

li m0 a2
2a
2

0
0 0
(4―45) (4―46)

lim
0
2
信号与系统周期信号的傅立叶级数展开

信号与系统周期信号的傅立叶级数展开


满足一定条件的周期函数 f ( t ) 可用三角函数集表示为
狄里 赫利
f(t)a 0 a nco sn0 tb nsinn0 t
n 1
0
2 T
条件
a0
1 T
t1T t1
f(t)dt
a n , bn
称为傅立叶系
数
an
t0 T t0
f (t) cos n0tdt
t0 T t0
cos2
n0tdt
信P87号图与4系-2-2统f( t) 4 [ s in0 t 1 3 s in 3 0 t 1 5 s in 5 0 t L 1 n s in n 0 t L ]
f1
(t)
4
sin
0tfLeabharlann 2(t)4
(sin 0t
1 3
sin
30t)
2
0
2 t
2
0
2 t
(a)
f
3
(t)
4
(sin
周期信号
周期信号的特点：
（1）它是一个无穷无尽变化的信号，从理论上也是无始无终的，时间
范围为(, )
（2）如果将周期信号第一个周期内的函数写成 f 0 ( t )，则周期信号 f ( t )
可以写成
f (t) f0(t nT) n
（3）周期信号在任意一个周期内的积分保持不变，即有
aT
bT
T
f(t)dt f(t)dtf(t)dt
f(t)A0Ancon s0tn
n1
两种形式之间系数有如下关系:
A0 a0
An an2 bn2
n 1, 2, L
或
n
arctg
方波信号的傅里叶变换

方波信号的傅里叶变换


信号的滤波
滤波器设计
通过傅里叶变换，可以将信号分解为 不同频率的分量，从而根据需要设计 滤波器，滤除特定频率范围的分量。
噪声抑制
在信号中混入噪声时，傅里叶变换可 以帮助识别和分离噪声分量，从而降 低噪声对信号的影响。
信号的压缩与扩展
压缩编码
通过对方波信号进行傅里叶变换，可 以将信号压缩为较小的数据量，便于 存储和传输。
方波信号的性质
01
方波信号具有明确的频率成分，其傅里叶变换可以 解析为简单的正弦和余弦函数。
02
方波信号的频率成分与其周期T有关，可以通过傅里 叶变换得到。
03
方波信号的波形因子a决定了其频谱的宽度和峰值。
方波信号的应用
1
方波信号在通信、控制、测量等领域有广泛应用 。
2
方波信号可以用于产生电磁波、调制载波等。
方波的频谱幅度随着谐波次数增 加而减小，呈现快速衰减的趋势 。
方波信号的频域特性周期性来自方波信号在频域内表现为一系列离散的谐波分量，这 些分量具有周期性重复的特点。
带宽有限
方波信号的频域特性表明其带宽是有限的，即其最高 频率分量是有限的。
能量集中
方波信号的能量主要集中在基频和较低次谐波上，高 次谐波携带的能量逐渐减少。
3
方波信号在数字电路中常被用作时钟信号。
02
CATALOGUE
傅里叶变换基础
傅里叶变换的定义
01
傅里叶变换是一种将时域信号转换为频域信号的方法。
02
对于给定的时域信号，通过傅里叶变换，可以得到该信号的频
谱。
傅里叶变换的基本公式为：(X(f) = int_{-infty}^{infty} x(t)
方波信号的傅里叶变换
方波信号傅里叶变换

方波信号傅里叶变换

从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
g r (t)
1
0
t 2
t 2
gτ(t)的傅里叶变换为
[ g r (t)]
2
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
An 3 3
2 2
1
0.8
0.4
o
2 3 4 5 6
(a )
n
45 °
45 °
30 ° 30 °
20 °
15 °
10 °
o
2
3
4
5
6
(b )
图 3.3-1 例 3.3-1
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
通信原理第7版第2章PPT课件(樊昌信版)

通信原理第7版第2章PPT课件(樊昌信版)


上式表明：周期信号可分解为直流和许多余弦分量。 其中， ● A0/2为直流分量； ● A1cos(t+1)称为基波或一次谐波，它的角频率（基频）与原周期信号相同 （ 2 ）； T
● A2cos(2t+2)称为二次谐波，它的频率是基波的2倍； ● 一般而言，Ancos(nt+n)称为n次谐波。
信号的正交分解
设有n个函数 1(t)， 2(t)，…， n(t)在区间 (t1，t2)构成一个正交函数空间。将任一函数f(t)用这 n个正交函数的线性组合来近似，可表示为 f(t)≈C11+ C22+…+ Cnn 问题：如何选择各系数Cj使f(t)与近似函数之间误差 在区间(t1，t2)内为最小？
为使上式最小（系数Cj变化时），有
2 Ci Ci

t2 t1
[ f (t ) C j j (t )]2 d t 0
j 1
n
展开上式中的被积函数，并求导。上式中只有两项 不为0，写为： t2 2 2 [ 2 C f ( t ) ( t ) C i i i i (t )]d t 0 Ci t1 即： 2
信号的正交分解
问题：如何选择各系数Cj使f(t)与近似函数之间误差 在区间(t1，t2)内为最小。
f(t)≈C11+ C22+…+ Cnn
通常两个函数误差最小，是指这两个函数在区间(t1， t2)内的的方均值（均方误差）最小。均方误差为：
n t2 1 2 2 [ f ( t ) C ( t ) ] dt j j t 2 t1 t1 j 18t源自 例2不满足条件2的一个函数是
2π f t sin , 0 t 1 t
方波信号的傅里叶级数

方波信号的傅里叶级数

方波信号的傅里叶级数方波信号是一种典型的周期性信号，可以通过傅里叶级数来进行分析和描述。

傅里叶级数是将一个周期性函数表示为各个正弦和余弦函数的线性组合，可以将复杂的周期性信号分解为简单的正弦和余弦函数的和。

本文将介绍方波信号的傅里叶级数及其应用。

让我们来了解一下什么是方波信号。

方波信号是一种在等间隔时间内交替出现两个不同幅值的信号。

它的特点是在每个周期内，信号的幅值从一个固定值突然跳变到另一个固定值，而且跳变的时间瞬间完成。

这种信号常见于数字电路中，也常用于信号处理和通信领域。

方波信号的傅里叶级数是将方波信号分解为各个正弦和余弦函数的和。

根据傅里叶级数的理论，任何一个周期性函数都可以表示为正弦和余弦函数的线性组合。

对于方波信号而言，它可以表示为各个奇次谐波的正弦函数的和。

通过逐渐增加奇次谐波的幅值和频率，可以逼近得到一个趋近于方波信号的函数。

傅里叶级数的应用非常广泛。

在通信领域，傅里叶级数可以用于信号的调制和解调。

通过将原始信号进行傅里叶级数分解，可以得到信号的频谱信息，从而实现信号的调制和解调。

在信号处理领域，傅里叶级数也被广泛应用于信号的滤波和谱分析。

通过对信号的傅里叶级数进行滤波操作，可以实现对信号频率的选择性处理。

而谱分析则可以通过对信号的傅里叶级数进行频谱分析，得到信号的频率分布情况，从而了解信号的特性和结构。

除了通信和信号处理领域，傅里叶级数还在其他领域有着广泛的应用。

在物理学中，傅里叶级数被用于描述波动现象和振动现象。

在工程学中，傅里叶级数可以用于描述动力系统的响应特性和频率响应。

在经济学和金融学中，傅里叶级数可以用于时间序列的分析和预测。

总结一下，方波信号的傅里叶级数是将方波信号表示为各个正弦和余弦函数的线性组合。

傅里叶级数的应用非常广泛，涉及到通信、信号处理、物理学、工程学、经济学等多个领域。

通过傅里叶级数的分析，可以深入理解和研究周期性信号的特性和结构。

傅里叶级数的研究和应用将为我们带来更深入的认识和理解，推动科学技术的进步和发展。

电子信号课件 4.4 三角形式的傅里叶级数

电子信号课件 4.4 三角形式的傅里叶级数

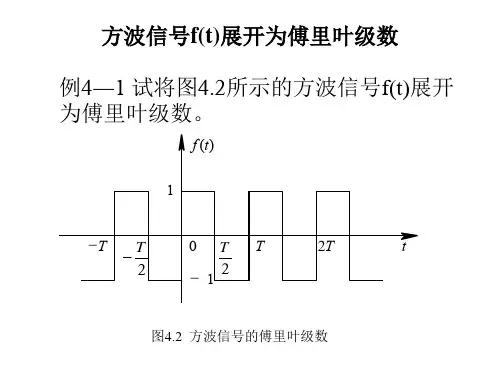
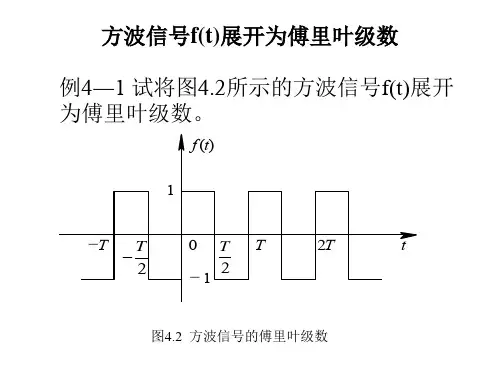
主要内容：1.周期信号三角形式的傅里叶级数2.狄里赫利条件3.吉布斯现象基本要求：1.掌握周期信号三角形式傅里叶级数和谐波的基本概念2.了解狄里赫利条件3.了解吉布斯现象的原理知识点Z4.4三角形式的傅里叶级数第四章 傅里叶变换与频域分析4.2周期信号的傅里叶级数Z4.4周期信号三角形式的傅里叶级数三角函数集{1，cos(nΩt)，sin(nΩt)，n=1,2,…}设周期信号f(t)，其周期为T，角频率Ω=2π/T，当满足狄里赫利(Dirichlet)条件时，可展开为三角形式的傅里叶级数。

系数an , bn称为傅里叶系数。

11()cos()sin() 2n nn naf t a n t b n t∞∞===+Ω+Ω∑∑1.三角形式的傅里叶级数11()cos()sin()2n n n n a f t a n t b n t ∞∞===+Ω+Ω∑∑222()cos()d T T n a f t n t tT-=Ω⎰余弦分量系数： 222()sin()d TT n b f t n t tT -=Ω⎰正弦分量系数：0221()d 2T T a f t tT-=⎰直流分量： 直流 n 次余弦分量n 次正弦分量2.狄里赫利(Dirichlet)条件：条件1：在一个周期内，函数连续或只有有限个第一类间断点；条件2：在一个周期内，函数极大值和极小值的数目应为有限个； 条件3：在一个周期内，函数绝对可积。

()f t O 18-t8212()sin(),(01)t f t t t=<≤O11-t1O121-2-t11(),(01)f t t t=<≤[]1()cos()sin()2n n n a f t a n t b n t ∞==+Ω+Ω∑合并n 次正余弦分量22arctann n n n n n A a b b a ϕ⎧=+⎪⎨=-⎪⎩cos sin n n nn n na Ab A ϕϕ=⎧⎨=-⎩01()cos()2n n n A f t A n t ϕ∞==+Ω+∑3.余弦形式的傅里叶级数A0/2 为直流分量；A 1cos(Ωt+ϕ1) 称为基波或一次谐波，角频率与原周期信号相同；A 2cos(2Ωt+ϕ2) 称为二次谐波；…A n cos(nΩt+ϕn) 称为n次谐波。

傅里叶变化例题


1
j
0
(4―40) (4―41)
F ( )
1
12
－ 0
(a)
argF()
2
4
－ 0
－
4
－
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
t
(a)
F(j )
2
o
解 门函数gτ(t)可表示为
g(t) 1
－τ2o
τ 2
t
(a)
F(j )
2
－4 －2 o
4
(b)
F( )
( )
－ 4
－
2
o
2 4
－4
－
2
o 2 4
－
(c)
(d)
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号GΤ(T)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
e( j )t
( j)
0
1
j
1
j arctan
e
a
a2 2
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t), a 0
F ( ) f (t)e jtdt eat e jtdt
f (t) 1
t
F ( j ) 1 e jtdt

方波信号的傅里叶变换

方波信号的傅里叶 变换
目录
• 方波信号概述 • 方波信号的傅里叶变换原理 • 方波信号的频谱分析 • 方波信号的滤波处理 • 方波信号的合成与调制 • 方波信号的傅里叶变换实例分析
01
CATALOGUE
方波信号概述
方波信号的定义
• 方波信号是一种常见的周期性信号，其特点是信 号在一定周期内以矩形波的形式重复。方波信号 在时间轴上的一个周期内，波形的最大值为1，最 小值为-1，波形在最大值和最小值之间以线性方 式变化。
03
CATALOGUE
方波信号的频谱分析
频谱的概念与计算
频谱定义
01
频谱是函数f(t)的傅里叶变换后的结果，它描述了函
数在各个频率下的强度和相位。
频谱计算
02 频谱可以通过将函数展开成无穷级数的方式进行计算
，即对函数进行傅里叶变换。
离散频谱
03
在实际应用中，我们通常处理的是离散频谱，即对连
续的频率取样后得到的频谱。
• 方波信号在通信系统中得到广泛应用，例如在数字通信中， 方波信号可以作为基带信号使用。此外，方波信号也常用于 模拟电路和数字电路的测试中，用于检测电路的响应和性能 。
02
CATALOGUE
方波信号的傅里叶变换原理
傅里叶变换的定义
01
02
03
傅里叶变换是一种数学 工具，可以将一个时域 信号转化为频域信号。 它可以将一个复杂的信 号分解为简单的正弦波 和余弦波的组合。
方波信号的基本性质
方波信号具有对称性，即在一个周期内，波形上升和下降的速度是相同的。这种对称性使得方波信号具有很好的直流分量， 即在一个周期内，信号的平均值为零。
方波信号的频谱具有离散性，即信号的频谱是由一些特定的频率分量组成的。这些频率分量对应于方波信号的基本周期和其 整数倍。

傅里叶级数


得信号的傅立叶展开式为： 得信号的傅立叶展开式为：
f (t ) = 1 4 1 1 sin(Ωt ) + sin(3Ωt ) + sin(5Ωt ) + ⋯ + sin( nΩt ) + ⋯, n = 1,3,5,⋯ π 3 5 n
它只含一、 奇次谐波分量。 它只含一、三、五、…奇次谐波分量。
n
因为傅里叶系数 将
an b 和
n
Fn =
1 1 1 An e jϕn = ( An cos ϕ n + jAn sin ϕ n ) = (an + jbn ) 2 2 2
系数公式带入上式得
1 Fn = T
∫
T 2
−T 2
1 f (t ) cos(nΩt )dt − j T
∫
T 2
−T 2
f (t ) sin(nΩt )dt
0, 2 = [1 − cos(nπ )] = 4 nπ nπ ,
n = 2,4,6,⋯ n = 1,3,5,⋯
将系数代入下面的式子： 将系数代入下面的式子：
∞ a0 ∞ f (t ) = + ∑ an cos(nΩt ) + ∑ bn sin( nΩt ) 2 n =1 n =1
某函数是否为奇（或偶）函数不仅与周期函数 某函数是否为奇（或偶）函数不仅与周期函数 的波形有关 而且与时间坐标原点的选择 有关， 时间坐标原点的选择有关 的波形有关，而且与时间坐标原点的选择有关 如下图是三角波的偶函数。 。如下图是三角波的偶函数。 f (t )
T 1 − 2 T 2
0
f (t )
坐标原点左移
∑Aeϕe
n
n

§4.3 周期信号的傅里叶级数

5
例4-3-1：将图示方波信号f(t)展开为傅里叶级数。
f (t )
1


T

T 2
0
1
T 2
T
3T 2
t
T 0 2 T 2 2 an 2T f (t ) cos(nt )dt T (1) cos(nt )dt 2 1 cos(nt )dt T 2 T 2 T 0 0 T 2 1 2 1 [ sin(nt )] T [sin(nt )] 2 T n T n 0 2
1 1 1 j n Fn An e ( An cos n jAn sin n ) (a n jbn ) 2 2 2
1 T

T 2 T 2
1 f (t ) cos( nt ) d t j T

T 2 T 2
1 f (t ) sin( nt ) d t T
2
2．级数形式
2 周期信号 f t , 周期为 T , 基波角频率为 2F T
n =1基波分量 直流分量
在满足狄氏条件时，可展成

f ( t ) a0 an cos nt bn sin nt
n 1
1
n >1谐波分量
称为三角形式的傅里叶级数，其系数
14
三．两种系数之间的关系及频谱图
1 Fn T
0
T
f (t )e j nt d t
利用欧拉公式
1 T 1 f (t ) cos nt d t j T 0 T 1 a n jbn 2
0
T
f (t ) sin nt d t
Fn
1 T
1 T
0

方波 傅里叶变换

方波傅里叶变换
方波是一种特殊的周期方波形，其周期为T，每个周期内的波形由一个矩形函数组成。

可以用傅里叶级数展开为：
f(t) = (4/pi) * [sin(w0t) + (1/3)sin(3w0t) + (1/5)sin(5w0t) + ...]。

其中，w0为基频，w0 = 2*pi/T。

傅里叶变换是将一个信号分解成不同频率的正弦和余弦信号的过程。

对于方波信号，它的频谱图是一系列的峰值，每个峰代表一个正弦或余弦信号的频率，并且峰值的高度与信号中该频率分量的相对强度成正比。

在频域中，方波信号的频谱具有奇函数性质，即其频谱图关于零点对称。

这是由于方波信号为奇函数，在傅里叶变换中只有正弦成分，没有余弦成分。

因此，它的频谱必须是奇函数。

通信原理第7版第2章樊昌信版

条件2：在一周期内，极大值和极小值的数目应是有 限个。
条件3:在一周期内，信号绝对可积。
例1
不满足条件1的例子如下图所示，这个信号的周期为8，它是这样 组成的：后一个阶梯的高度和宽度是前一个阶梯的一半。可见在 一个周期内它的面积不会超过8，但不连续点的数目是无穷多个。
8
f t
1
1 2
O
8t

3
5
n
基波 1.5
1
0.5
0
-0.5
-1
-1.5
0
1
2
3
4
5
6
t
基波＋三次谐波
1 0.5
0 -0.5
-1
0
1
2
3
4
5
6
t
基波＋三次谐波＋五次谐波
1 0.5
0 -0.5
-1
0
1
2
3
4
5
6
t
基波＋三次谐波＋五次谐波＋七次谐波
1 0.5
0 -0.5
-1
0
1
2
3
4
5
6
t
傅里叶级数的指数形式
三角形式的傅里叶级数，含义比较明确，但运算常感 不便，因而经常采用指数形式的傅里叶级数。
● A0/2为直流分量； ● A1cos(t+1)称为基波或一次谐波，它的角频率（基频）与原周期信号相同 （ 2 ）；
T
● A2cos(2t+2)称为二次谐波，它的频率是基波的2倍； ● 一般而言，Ancos(nt+n)称为n次谐波。
例：将图示方波信号f(t)展开为傅里叶级数。
e j t cos t j sin t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(j)
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
－
4
－
2
o
4
(b )
F( )
( )
－
4
－
2
o
2 4
－
4
－
2
o 2 4
－
(c)
(d )
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
g r (t)
1
0
t 2
t 2
gτ(t)的傅里叶变换为
[ g r (t)]
2
2
e jtdt sin( / 2) /2
方波信号f(t)展开为傅里叶级数
例4―1 试将图4.2所示的方波信号f(t)展开 为傅里叶级数。
f (t)
1
－T T
0T T
2T
t
2
－1 2
图4.2 方波信号的傅里叶级数
解 我们将信号按式(4―6)分解成傅里叶级数,
并按式(4 及c。
―
7)、(4―8)、(4―9)分别计算an,
bn
an
2 T
T
双边指数信号的频谱。 解 双边指数信号是指
f(t)etu(t), 0 (4―42)
从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
An 3 3
2 2
1
0.8
0.4
o
2 3 4 5 6
(a )
n
45 °
45 °
30 ° 30 °
20 °
15 °
10 °
o
2
3
4 5
6
(b )
图 3.3-1 例 3.3-1
(a) 振幅谱； (b) (b) 相位谱
|F n |
2
1 .5
1 .5
1
1
1
0 .4 0 .2
0 .4 0 .2
－ 6－ 5 － 4－ 3－ 2 － o
0
(4―40) (4―41)
F()
1
12
－ 0
(a)
argF()
2 4
－ 0
－
4
－
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
t
(a)
F(j)
2
o
(b)
图 3.4-3 (a) 双边指数函数； (b) 频谱
0 T
2
(1)sin(2nft)dt 2
T
T 2 0
1 sin(2nft)dt
2 T
1
2 nft
[ cos(2 nft)]
0 T
2
2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
4
n
n 2,4,6, n 1,3,5,
c2 T
T
2 T
2
f(t)dt0
f(t)4[sin2ft13sin6ft15sin10f
f(t)A 20n 1Ancon st(n)
可知，其基波频率Ω=π(rad/s)，基本周期T=2 s，ω=2π、3π、 6 π分别为二、 三、六次谐波频率。且有
A0 1 2
A1 3
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
2 3 4 5 6
(a )
n 45°
45°
30° 30°
20°
15° 10°
－ 6－ 5 － 4－ 3 － 2 － o
2 3 4 5 6
－ 10° － 15°
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
单边指数函数f(t)的频谱函数
(a>0)
t 0
F(j) 0eaet jtdt etejtdt
0
1 1
j j
j
2 a2 2
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
g (t ) 1
－τ
1sin2ft]
n
n1,3,5,
振幅谱和相位谱例题
例 3.3-1 f(t)13cots1 (0 )2co2st (20 ) 0.4co3st (45 )0.8co6st (30 ),
试画出f(t)的振幅谱和相位谱。 解 f(t)为周期信号，题中所给的f(t)表达式可视为f(t)的傅里
叶级数展开式。据
例 3.4-2 求指数函数f(t)的频谱函数。
f
(t)
e at
t 0
0
t 0
f (t)
1 e－t (＞0)
(0)
F()
1
o
t
o
(a)
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F(j) f(t)ejtdt etejtdt
e(j)t
解
F(j) (t)ejtd t1
Sa(x) sin( x) x
[
g
r
(t)]
Sa(
2
)
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
f (t)
F(j)
1
(t)
o
t
(a)
o
(b)
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
X( )
1
o
t
－ et
o
－1 (a)
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
－
1
(b)
解 图示信号f(t)可表示为
f
(t)
e at
e at
t 0