苏教版五年级上册图形面积计算

苏教版五年级数学上册核心考点专项评价2. 规则图形的面积计算一、认真填空。

(每空 2 分，共 22 分)1．把一个平行四边形沿高剪开，拼成一个长方形(如下图) ，它的面积与原来平行四边形的面积( )，长方形的长相当于平行四边形的 ( )，长方形的宽相当于平行四边形的( )，所以平行四边形的面积等于( )，用字母表示是( )。

2．如图，一个长方形的长为 8 分米，宽为 4 分米，把四条边的中点顺次连接起来，阴影部分的面积是( )平方分米。

3．一个等边三角形的周长是 21 分米，高约是 6 分米，它的面积约是( )平方分米。

4．一个平行四边形，相邻两边的长度分别是12厘米和 9 厘米，其中一边上的高是 10厘米，这个平行四边形的面积是( )平方厘米。

5．【南京市】用长 4 分米、宽 25 厘米的长方形彩纸做成直角三角形小旗，每面小旗的两条直角边分别长 10 厘米、12 厘米，最多可以做( )面这样的小旗，每面小旗的面积是 ( )平方厘米。

6．如图，一个长方形ABCD的长是10厘米，宽是 6 厘米，那么平行四边形BEFD的面积是( )平方厘米。

二、慎重选择。

(每题 3 分，共 18 分)1．如图，已知涂色部分的面积是 10 平方分米，则空白部分的面积是( )平方分米。

A．12 B．15C．18 D．202．两个完全一样的平行四边形中，阴影部分①的面积( )阴影部分②的面积。

A．大于B．等于C．小于D．无法确定3．如图，一块腰长是 8 分米的等腰直角三角形玻璃被打碎了，这块玻璃原来的面积是( )平方分米。

A．64B．32C．16D．1284．如果平行四边形的面积是 42 平方厘米，将底平均分成 3 份，那么图中阴影部分的面积是( )平方厘米。

A．14B．42C．28D．75．如图，每个小正方形的面积是 2cm2，涂色部分的面积是 ( )cm2。

A．32B．34C．20D．406．下面四个图形中，面积相等的是( )。

五年级上册数学教案-第二单元组合图形面积的计算-苏教版一、教学目标1.掌握组合图形面积的计算方法。

2.能够根据所给条件计算组合图形的面积。

3.培养学生的空间想象力和计算能力。

二、教学重点1.理解组合图形的概念及构成。

2.掌握组合图形面积的计算方法。

三、教学难点1.解决组合图形的面积计算问题。

2.发现组合图形中的规律。

四、教学准备1.教师准备：教学教材、黑板笔、教学PPT。

2.学生准备：学习用书、笔记本、尺子、铅笔、橡皮。

五、教学过程1. 导入1.通过教学PPT展示几种组合图形（如长方形与半圆组成图形等）。

2.讲解组合图形的定义，并让学生进行回答互动。

2. 推导组合图形面积计算公式1.以长方形与半圆组成的图形为例，提问学生对它的面积计算方法。

2.对答案进行讲解后，用黑板进行图形的细化，让学生自行进行计算。

3.汇总结果，推导出组合图形面积计算公式。

3. 练习1.在黑板上展示几个组合图形，要求学生自行计算它们的面积。

2.让学生交流并互相检验答案，及时纠错。

4. 总结1.让学生得出本节课的知识点和难点，并通过PPT进行展示。

2.总结教学内容，强化学生的记忆。

六、作业1.完成课堂练习题。

2.课后作业：纸上练习，巩固相关知识点。

七、教学反思通过本节课的教学，我发现学生比较容易在理解组合图形的过程中犯错误，导致面积计算的答案出错。

针对这一问题，我增加了对组合图形的细化步骤，并在课堂练习中加强了学生的相互检验。

此外，我还结合实际情况，引入了一些有趣的案例，增强了学生的兴趣，提升了教学效果。

苏教版五年级上册《平行四边形面积计算》说课稿一. 教材分析苏教版五年级上册《平行四边形面积计算》这一课，是在学生已经掌握了四边形的特征，长方形、正方形的面积计算的基础上进行教学的。

通过这一课的学习，使学生掌握平行四边形的面积计算方法，发展学生的空间观念，培养学生的抽象思维能力。

二. 学情分析五年级的学生已经具备了一定的几何图形知识，对四边形有了一定的认识，同时也掌握了长方形和正方形的面积计算方法。

但学生在学习过程中，可能对于平行四边形面积计算公式的推导过程，还存在一定的困难。

因此，在教学过程中，我将以学生为主体，引导学生通过观察、操作、思考、讨论等方式，自主探索平行四边形的面积计算方法。

三. 说教学目标1.知识与技能目标：学生能够理解平行四边形的面积计算公式，并能够运用公式计算平行四边形的面积。

2.过程与方法目标：通过学生的自主探究、合作交流，培养学生的观察能力、操作能力、思考能力。

3.情感态度与价值观目标：培养学生对数学的兴趣，培养学生勇于探索、积极思考的精神。

四. 说教学重难点1.教学重点：学生能够掌握平行四边形的面积计算公式，并能够运用公式计算平行四边形的面积。

2.教学难点：学生能够理解并推导出平行四边形的面积计算公式。

五. 说教学方法与手段在本节课的教学过程中，我将采用引导发现法、合作交流法、操作实验法等教学方法，以多媒体课件为辅助教学手段，引导学生观察、操作、思考、讨论，从而自主探索出平行四边形的面积计算方法。

六. 说教学过程1.导入新课：通过多媒体课件展示生活中的平行四边形物体，引导学生回顾平行四边形的特征，为新课的学习做好铺垫。

2.自主探究：让学生通过剪、移、拼等操作，将平行四边形转化为已知的图形，从而推导出平行四边形的面积计算公式。

3.合作交流：学生分小组进行讨论，分享自己的探究过程和结果，互相学习，互相启发。

4.教师讲解：教师根据学生的探究结果，进行总结讲解，使学生明确平行四边形的面积计算公式。

苏教版五年级数学上册《平行四边形面积的计算》公开课说课稿一. 教材分析苏教版五年级数学上册《平行四边形面积的计算》这一节课，主要让学生掌握平行四边形的面积计算方法。

教材通过简单的实例和具体的操作，引导学生探究平行四边形面积的计算公式，并能够运用该公式解决实际问题。

教材还注重培养学生的空间观念和动手操作能力，提高他们解决实际问题的能力。

二. 学情分析五年级的学生已经掌握了四边形的性质，具备了一定的观察和操作能力。

他们对平行四边形的概念有一定的了解，但是对平行四边形面积的计算方法还不够熟悉。

因此，在教学过程中，我将以学生为主体，引导学生通过观察、操作、思考、交流等方式，自主探索平行四边形面积的计算方法。

三. 说教学目标1.知识与技能目标：让学生掌握平行四边形的面积计算方法，能够运用该公式解决实际问题。

2.过程与方法目标：通过观察、操作、思考、交流等过程，培养学生的空间观念和动手操作能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养他们独立思考、合作交流的良好习惯。

四. 说教学重难点1.教学重点：平行四边形的面积计算方法。

2.教学难点：理解平行四边形面积计算的原理，能够灵活运用公式解决实际问题。

五. 说教学方法与手段1.教学方法：采用问题驱动法、启发式教学法、合作交流法等。

2.教学手段：利用多媒体课件、实物模型、操作卡片等辅助教学。

六. 说教学过程1.导入新课：通过展示平行四边形的图片，引导学生回顾平行四边形的性质，为新课的学习做好铺垫。

2.探究平行四边形面积计算方法：（1）观察实例：展示平行四边形的实物模型，引导学生观察并思考平行四边形的面积如何计算。

（2）小组讨论：让学生分组讨论，分享各自的思考和见解。

（3）总结公式：引导学生通过观察、操作、思考等过程，总结出平行四边形面积的计算公式。

3.实践操作：让学生利用操作卡片，亲自动手操作，验证平行四边形面积的计算公式。

4.解决问题：运用所学的平行四边形面积计算方法，解决实际问题。

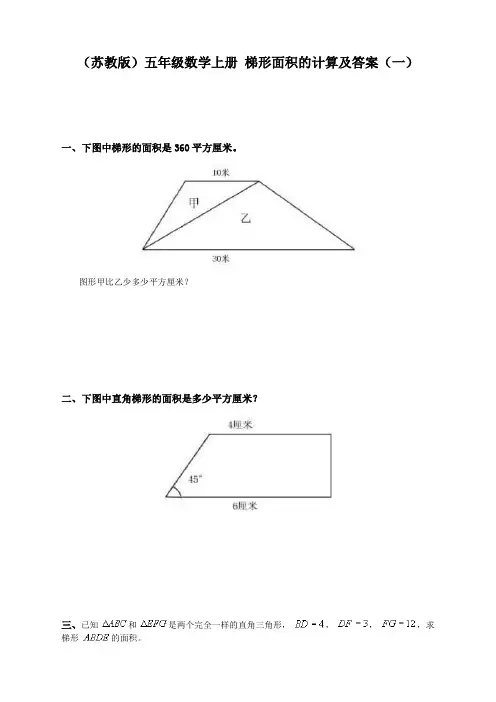
（苏教版）五年级数学上册梯形面积的计算及答案（一）一、下图中梯形的面积是360平方厘米。

图形甲比乙少多少平方厘米？二、下图中直角梯形的面积是多少平方厘米？三、已知和是两个完全一样的直角三角形，，，，求梯形的面积。

四、一个梯形，它的高与上底的乘积是15平方厘米，高与下底的乘积是21平方厘米，这个梯形的面积是多少平方厘米？五、一个直角梯形，若下底增加1.5米，则面积就增加3.15平方米，上底增加1.2米，就得到一个正方形。

这个直角梯形的面积是多少平方米？参考答案一、解：360×2÷（10＋30）＝18（厘米）10×18÷2＝90（平方厘米）30×18÷2＝270（平方厘米）270－90＝180（平方厘米）思路二：根据梯形的性质，上底和下底平行，所以甲和乙这两个三角形的高相等。

由已知条件乙三角形的底是甲三角形底的3倍（30÷10），所以乙的面积是甲的3倍，即乙的面积比甲多2倍。

梯形面积一共是360平方米，一共分成4份，一份是90平方米，所以甲比乙少90×2＝180平方米。

解：30÷10＝3360÷（3＋1）×（3－1）＝90×2＝180（平方米）答：甲的面积比乙少180平方厘米。

二、连出的三角形为等腰直角三角形，这就得出梯形的高就是2厘米，解决了关键问题。

解：（4＋6）×2÷2＝10（平方厘米）。

三、解：在梯形中，，，（8＋12）×3÷2＝30答：梯形的面积是30。

四、分析：根据题意可知：高×上底＝15，高×下底＝21，所以高×上底＋高×下底＝（上底＋下底）×高（乘法分配率）又因为（上底＋下底）×高＝梯形面积×2即15＋21＝36是梯形面积的2倍解：（15＋21）÷2＝18（平方厘米）答：梯形面积是18平方厘米。

苏教版五年级上多边形的面积整理与练习在五年级上册的数学学习中，多边形的面积是一个重要的知识点。

它不仅帮助我们更好地理解几何图形，还为解决实际问题提供了有力的工具。

接下来，让我们一起对这部分内容进行整理和练习。

一、多边形的分类及特点我们首先来了解一下常见的多边形。

多边形是由若干条线段首尾顺次相连组成的封闭图形。

1、三角形三角形是最基本的多边形，它具有稳定性。

按角分类，可以分为锐角三角形、直角三角形和钝角三角形；按边分类，可以分为等边三角形、等腰三角形和不等边三角形。

2、平行四边形平行四边形的两组对边分别平行且相等，它具有不稳定性。

3、梯形梯形只有一组对边平行。

二、多边形面积的计算公式1、三角形的面积三角形的面积＝底×高÷2，如果用字母表示，即 S ＝ ah÷2（其中 a 表示底，h 表示高）。

例如，一个三角形的底是 6 厘米，高是 4 厘米，那么它的面积就是6×4÷2 ＝ 12（平方厘米）。

2、平行四边形的面积平行四边形的面积＝底×高，用字母表示为 S ＝ ah。

比如，一个平行四边形的底是 8 厘米，高是 5 厘米，面积就是 8×5 ＝ 40（平方厘米）。

3、梯形的面积梯形的面积＝（上底＋下底）×高÷2，用字母表示为 S ＝（a ＋b）h÷2（其中 a 表示上底，b 表示下底，h 表示高）。

假设一个梯形的上底是 3 厘米，下底是 7 厘米，高是 5 厘米，其面积为（3 ＋ 7）×5÷2 ＝ 25（平方厘米）。

三、多边形面积公式的推导1、三角形面积公式的推导我们可以通过将两个完全一样的三角形拼成一个平行四边形，因为平行四边形的面积＝底×高，所以一个三角形的面积就是这个平行四边形面积的一半，即三角形的面积＝底×高÷2。

2、平行四边形面积公式的推导通过沿着平行四边形的高剪开，然后平移拼成一个长方形。

第6讲简单几何图形的面积【知识要点】平行四边形的面积公式：底×高S=a⨯h三角形的面积公式：底×高÷2=h⨯2aS÷梯形的面积公式：梯形的面积＝（上底＋下底）×高÷2+=h（bS÷⨯)2a【经典例题】【例1】(★)把下面的图形分成已经学过的图形.【练习1】（★）下面各图形是什么图形缺少了一部分.【例2】(★★)计算下面图形的面积.【练习2】（★★）计算下面图形的面积.【例3】（★★）计算下面图形的面积，你有几种方法？【练习3】（★★）计算下面图形的面积，你有几种方法？【例4】（★★）“六一”儿童节那天，英华小学在校门口用花盆摆成如下图所示的图案，你能算出这个图案的面积吗？【练习4】（★★）某块菜地的形状如图，这块菜地的占地面积是多少平方米？【例5】（★★）一块梯形草地中间有一条长8米，宽1米的长方形小路(如图，单位：m)，这块草地的面积是多少平方米？【练习5】（★★）下图是一块长方形的草地，长是16米，宽是10米，中间有两条道路，一条是长方形，一条是平行四边形，那么有草部分的面积有多大？【例6】（★★）从下面的梯形中剪去一个最大的三角形，剩下部分的面积是多少？【练习6】（★★）美术课上，黄老师让小雯在一张上底是30厘米、下底是40厘米、高是30厘米的直角梯形白纸上，画一幅最大的正方形水彩画，剩下的白纸的面积是多少？【例7】（★★）下图中梯形的面积是9平方米，求阴影部分的面积.【练习7】（★★）求下面图形中阴影部分的面积.（梯形面积为8平方米）【例8】（★★★）如图是一个平行四边形，它包含了三个三角形，其中两个白三角形的面积15平方厘米和25平方厘米，中间涂色的三角形面积是____平方厘米.【练习8】（★★★）如图，AD=DC，AE=EB.若阴影部分的面积是20cm2，则三角形ABC的面积是( ) cm2.【课后练习】1.（★）计算下面图形的面积.2.（★★）求阴影部分的面积(单位：米).3.（★★）图中长方形的面积是220cm，那么，空白的两个三角形①、②面积的和是( ) 2cm.4.（★★）如图，边长相等的两个正方形中，画了甲、乙两个三角形(用阴影表示)，它们的面积相比：甲乙.（填“大于”“小于”或“等于”）5.（★★）一把雨伞的伞面是由8块相同的三角形布料拼成的.每个三角形的底是37厘米，高是48厘米.做这把雨伞至少要用多少平方米的布料？(得数保留两位小数)6.（★★）一块平行四边形麦田，中间有一条宽1.5m的小路.（1）这块麦田的面积是多少平方米？（2）如果每平方米收小麦约0.75kg，这块地大约能收小麦多少千克？7.（★★）公园里有两块空地，计划分别种玫瑰和牡丹.占地面积价格①②（1）玫瑰园占地多少平方米？种玫瑰一共需要多少元？（2）你还能提出什么数学问题？并尝试解答.8.（★★）这是小东在计算下面图形的面积的方法，请你判断下：他做的对吗？如果不对，请改正过来.9.（★★★）如图，是一张长方形卡纸和一张三角形卡纸重叠在一起的图形.已知长方形卡纸的面积比三角形卡纸的面积小16cm2，三角形底边CE的长是多少厘米？(单位：cm)10.（★★★）如图，直角梯形的上下底分别是6cm、10cm，高为8cm，如果用虚线把梯形分成面积相等的两部分，那么AB的长度是多少cm？cm. 11.（★★★）大正方形的边长是9cm，小正方形的边长是5cm.阴影部分的面积是____212.（★★★）计算下图阴影部分的面积.。

9图形的面积例1、如图，已知三角形ABC的面积是24平方厘米，AD=DB，CE=2BE，求三角形BDF的面积。

例2、如图△ABC与△ADE都是等腰直角三角形，BC长8厘米，D E长4厘米，求阴影部分的面积。

例3、如图，边长为10和15厘米的两个正方形并排放在一起，求三角形ABC（阴影部分）的面积。

例4、如图，AD=EC=4厘米，BD=BE=6厘米，那么图中阴影部分的面积是多少平方厘米？例5、如图，正方形ABCD的面积为1，E是BC边上的中点，求图中阴影部分的面积。

练习1、如图，BE=3AB，BC=CD，三角形ABC的面积是15平方厘米，求三角形BDE的面积。

2、如图，三角形ABC的面积是10平方厘米，将AB、BC、CA分别延长一倍到点D、E、F，两两连结D、E、F、，得到一个新的三角形DEF，求三角形DEF的面积。

3、如图，三角形ABC的面积是72平方分米，BD=2DC，AE=ED，两个阴影三角形的面积是多少平方分米？4、如图，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长9厘米，下底长5厘米的等腰梯形（阴影部分），求这个等腰梯形的面积。

5、两块等腰直角三角形的塑料板，按如图所示的位置那样重叠，求重叠部分（阴影部分）的面积。

（单位：厘米）6、如图，AE=12厘米，BC=6厘米，ED=3厘米，∠C=135°，四边形ABCD的面积是多少平方厘米？7、如图，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等。

如果AB=9厘米，FB=FE，求三角形AFE的面积。

8、如图，线段BG将一个边长10分米的正方形分成两个高相等（AF=FD）的直角梯形和一个直角三角形，已知线段EF分成两个梯形面积的差是10平方分米，则图中的x的长是多少分米？9、如图，四边形ABCD是一个正方形，边长是6厘米，E、F分别是CD、BC的中点，求阴影部分的面积。

10、如图，四边形ABCD是一个梯形，E是AD的中点，CE把梯形分成一个三角形甲和一个四边形乙，甲的面积是3，乙的面积是5，则下底CD长度是上底AB长度的几倍？图形的面积——练习1、如图两个等腰直角三角形ABC和DEF的直角边分别长16厘米和12厘米。