五年级上册图形面积计算
- 格式:docx
- 大小:140.49 KB
- 文档页数:4

多边形的面积一、计算公式注:S表示面积,a表示底,h表示高,底和高必须对应!在梯形的面积公式里,a表示上底,b表示下底,一般来说,短的是上底,长的是下底。
在计算面积时,要找准对应的量。
求三角形和梯形的面积时,不要忘了除以2。
二、其他知识点1、计算多边形的面积,要代入公式计算。
2、推导平行四边形的面积,将平行四边形转化成长方形。
(割补法)3、平行四边形的周长=相邻两边长之和×2 三角形的周长=三条边之和梯形的周长=上底+下底+两条腰4、把一个长方形拉成平行四边形,周长不变,面积变小(平行四边形的高比原来长方形的宽小)。
反之,把平行四边形拉成一个长方形,周长不变,面积变大。
5、两个完全一样的三角形可以拼成一个平行四边形。
(拼摆法)6、等底等高的平行四边形和三角形,平行四边形的面积是三角形面积的2倍,三角形面积是平行四边形面积的一半。
等面积等底的平行四边形和三角形,三角形的高是平行四边形的高的2倍,平行四边形的高是三角形的高的一半。
7、在直角三角形里,两条直角边就是对应的底和高,斜边最长。
8、两个完全一样的梯形可以拼成一个平行四边形。
(拼摆法)9、计算堆成梯形形状的圆木、钢管等的个数,通常用下面的方法:(顶层个数+底层个数)×层数÷2=总个数。
注意:只有下一层物体比上一层物体数多1时,才有“层数=底层个数-顶层个数+1”10、求组合图形的面积时,一定要找准所分成的图形的相关数据。
11、不规则图形的面积可以转化成学过的图形来估算,也可以通过数方格的方法来估算。
三、解答方法1、计算面积时,分清是算哪种图形的面积,直接利用相应的面积公式,一定要找准公式里所需的每个量,注意单位是否一致,算出结果后记得写单位,面积单位有“平方”两个字。
2、计算底、高、上底或下底时,同样看清是哪种图形,直接利用相应面积公式的变式。
(熟记和熟练运用上面表格的计算公式。
)3、计算组合图形的面积时,利用割补法,看清组合图形是由哪几个简单图形(所谓简单图形,就是我们学过的长方形、正方形、平行四边形、三角形、梯形)组成的,分别算出每个简单图形的面积,最后不要忘了再相加(分割法,图形是凸的)或相减(添补法,图形是凹的)。

人教版五年级上册《多边形的面积》要点知识及易错点解析《多边形的面积》要点知识一、公式:多边形面积公式面积公式的变式说明正方形正方形的面积=边长X边长S正=aXa=a2已知:正方形的面积,求边长长方形长方形的面积=长X宽S长=aXb已知:长方形的面积和长,求宽平行四边形平行四边形的面积=底X高S平=aXh已知:平行四边形的面积和底,求高h=S平÷a三角形三角形的面积=底X宽高÷2S三=aXh÷2已知:三角形的面积和底,求高H=S三X2÷a梯形梯形形的面积=(上底+下底)X高÷2S梯=(a+b)X2已知:梯形的面积与上下底之和,求高高=面积×2÷(上底+下底)上底=面积×2÷高-下底组合图形当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。
当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
二、平行四边形面积公式推导:剪拼、平移平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底;长方形的宽相当于平行四边形的高;长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
三、三角形面积公式推导:旋转两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2四、梯形面积公式推导:旋转两个完全一样的梯形可以拼成一个平行四边形。
平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷2五、等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍。


小学五年级上册数学《三角形面积的计算》教案(精选7篇)小学五年级上册数学《三角形面积的计算》篇1教学内容:教材第9—10页例4、例5及“练一练”、“试一试”、“练习二”第6-9题。
教学目标:1.通过操作、观察、填表、讨论、归纳等数学活动,探索并掌握三角形的面积公式,能正确地计算三角形的面积,并应用公式解决简单的实际问题。
2.进一步体会转化方法的价值,培养自己应用已有知识解决新问题的能力,发展自己的空间观念和初步的推理能力。
教学重点:经历探究三角形面积计算公式的过程,理解并掌握三角形的面积计算公式。
教学难点:理解三角形面积公式的推导过程。
教学准备:多媒体、教材第115页的三角形。
探究方案:一、自主准备1.说一说:下面每个小方格表示1平方厘米,你知道涂色三角形的面积各是多少平方厘米吗?你是怎么想的?()()()2.思考:(1)三角形的面积与它拼成的平行四边形的面积有什么关系?(2)有没有直接计算三角形面积的方法呢?(3)假如要你探究三角形的面积,你打算把它转化成什么图形进行研究?我想转化成二、自主探究1.拼一拼:从课本第115页上选两个完全一样的三角形剪下来,看看能不能拼成平行四边形。
2.填一填:你剪下的两个完全一样的三角形能拼成平行四边形吗?如果能,拼成的平行四边形的面积和每个三角形的面积各是多少?请填写下表。
3.想一想(1)拼成平行四边形的两个三角形有什么关系?(2)拼成的平行四边形的底和高与原三角形的底和高有什么关系?每个三角形的面积与拼成的平行四边形的面积呢?(3)根据平行四边形的面积公式,怎样求三角形的面积?三、自主应用试一试:完成书上第10页的“试一试”。
四、自主质疑说一说:(1)三角形的面积公式是怎么推导的?你还有什么疑问?(2)你认为本节课应学会什么?教学过程:一、明确目标提问:同学们,通过自主学习,你知道今天的学习内容吗?(揭示课题)你认为本节课应学会什么?二、交流提升1.出示例4的方格图及其中的平行四边形。
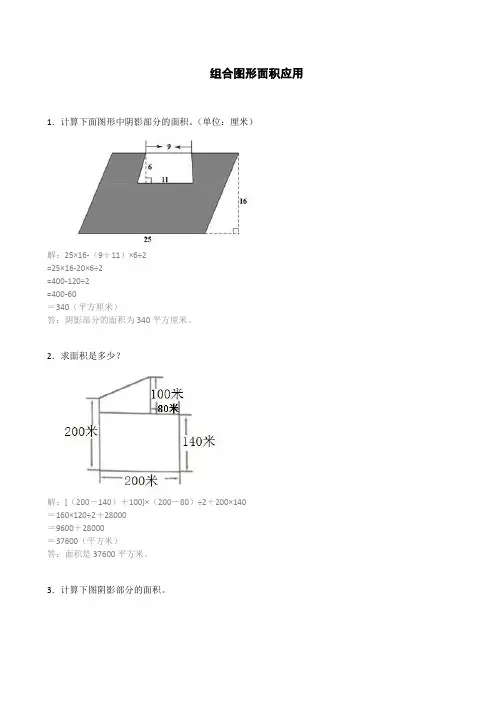
组合图形面积应用1.计算下面图形中阴影部分的面积。
(单位:厘米)解:25×16-(9+11)×6÷2=25×16-20×6÷2=400-120÷2=400-60=340(平方厘米)答:阴影部分的面积为340平方厘米。
2.求面积是多少?解:[(200-140)+100]×(200-80)÷2+200×140=160×120÷2+28000=9600+28000=37600(平方米)答:面积是37600平方米。
3.计算下图阴影部分的面积。
解:阴影部分的面积=(10+15)×10÷2-10×10÷2 =25×10÷2-100÷2=250÷2-50=125-50=75(平方米)。
4.计算阴影部分的面积。
(单位:cm)解:60×40-60×40÷2=2400-2400÷2=2400-1200=1200(平方厘米)5.求下面组合图形的面积。
(单位:cm)解:8×4+8×4÷2=32+32÷2=32+16=48(平方厘米)6.计算下面阴影部分的面积。
(1)(2)(1)解:阴影部分的面积=14×12÷2=168÷2=84(平方厘米)(2)解:阴影部分的面积=12×10-12×6÷2=120-72÷2=120-36=84(平方分米)(2)阴影部分的面积=平行四边形的面积-三角形的面积,平行四边形的底是20dm,高是10dm;三角形的底是20dm,高是6dm,再根据平行四边形的面积=底×高,三角形的面积=底×高÷2,代入数值计算即可。
7.计算下面图形的面积。

小学数学五年级上册图形计算公式Prepared on 21 November 2021五年级上册图形计算公式 正方形的面积=S=正方形的周长=c =长方形的面积=S= 长方形的周长=c = 平行四边形的面积=S= 底=a = 高=h =三角形形的面积=S= 底=a =高=h =梯形形的面积=S=(上底+下底)=(a+b )=上底=a =下底=b =高=h =5、梯形面积公式的推导过程:把两个完全一样的梯形可以拼成一个平形四边形,拼成平形四边形的底等于梯形的上底加下底的和,平行四边形的高与梯形的高相等,每个梯形的面积是拼成平形四边形面积的一半,因为平形四边形面积等于底乘以高,所以梯形等于(上底+下底)×高÷2.如果用S 表示梯形的面积,用a 、b 和h 分别表示梯形的上底和高,面积公式可以写成S=(a+b)h÷2梯形的面积=(上底+下底)×高÷2?S 梯=(a+b )h÷2梯形的高=面积×2÷(上底+下底)h 梯=S×2÷(a+b )上底+下底=面积×2÷高?a+b=S×2÷h梯形的上底=面积×2÷高-下底?a 梯=S×2÷h-b梯形的下底=面积×2÷高-上底?b 梯=S×2÷h-a1.长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米 aa aba hah2.面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米?l平方厘米=100平方毫米3.重量单位换算1吨=1000千克1千克=1000克1千克=1公斤4.人民币单位换算‘1元=10角1角=10分1元=100分5.时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月?平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时?1时=6O分1分=60秒1时=3600秒6.数量关系式(1)、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数(2)、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数(3)、速度×时间=路程路程÷速度=时间路程÷时间=速度(4)、单价×数量=总价总价÷单价=数量总价÷数量=单价(5)、工作效率×工作时间=工作总量?工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率(6)、加数+加数=和?和-一个加数=另一个加数(7)、被减数-减数=差?被减数-差=减数?差+减数=被减数(8)、因数×因数=积?积÷一个因数=另一个因数(9)、被除数÷除数=商被除数÷商=除数商×除数=被除数7.角和三角形(1)角的大小分类,从小到大是:锐角、直角、钝角、平角、周角(2)锐角是小于90度的角,直角是90度,钝角是大于90度而小于平角的角,平角是180度的角,周角是360度的角。



五年级上册图形面积专项训练题库及答案研究必备,欢迎下载!以下是一些计算题和图形面积专项训练题。
1.计算下列图形的面积(单位:cm):长4cm,宽5cm的矩形:4 × 5 = 20平方厘米底边长3cm,高8cm的三角形:3 × 8 ÷ 2 = 12平方厘米底边长8cm,高10cm的三角形:8 × 10 ÷ 2 = 40平方厘米底边长8cm,高7cm的梯形:(8 + 10) × 7 ÷ 2 = 56平方厘米底边长9cm,高8cm的梯形:(9 + 7) × 8 ÷ 2 = 64平方厘米2.计算下列图形的面积:长10m,宽24m的矩形:10m × 24m = 240平方米底边长40m,高12m的三角形:40m × 12m ÷ 2 = 240平方米一个由两个矩形组成的图形,其中一个矩形的长是14cm,宽是16cm,另一个矩形的长是18cm,宽是25cm,它们的高都是12cm:(14 × 12 ÷ 2 + 16 × 12 ÷ 2) + (18 × 12 ÷ 2 + 25 × 12 ÷ 2) = 180 + 252 = 432平方厘米3.计算下列三角形的面积:底边长8.6m,高2.7m:8.6m × 2.7m ÷ 2 = 11.61平方米底边长10dm,高7.3dm:10dm × 7.3dm ÷ 2 = 36.5平方分米4.根据已知条件填表:底为6cm,高为5cm的三角形面积为4.2平方厘米底为4cm,高为1.2cm的三角形面积为2.4平方厘米底为12cm,高为3cm的三角形面积为18平方厘米5.一个停车场是平行四边形,底边长为63米,高为25米,每辆车平均占地15平方米。

小学数学五年级上册
《组合图形的面积》资料计算公式
长方形:
{长方形面积=长×宽}
正方形:
{正方形面积=边长×边长}
平行四边形:
{平行四边形面积=底×高}
三角形:
{三角形面积=底×高÷2}
梯形:
{梯形面积=(上底+下底)×高÷2}
圆形(正圆):
{圆形(正圆)面积=圆周率×半径×半径}
圆环:
{圆形(外环)面积={圆周率×(外环半径^2-内环半径^2)} 扇形:
{圆形(扇形)面积=圆周率×半径×半径×扇形角度/360}
长方体表面积:
{长方体表面积=(长×宽+长×高+宽×高)×2}
正方体表面积:
{正方体表面积=棱长×棱长×6}
球体(正球)表面积:
{球体(正球)表面积=圆周率×半径×半径×4}
椭圆
(其中π(圆周率,a,b分别是椭圆的长半轴,短半轴的长). 半圆:
(半圆形的面积公式=圆周率×半径的平方÷2)。
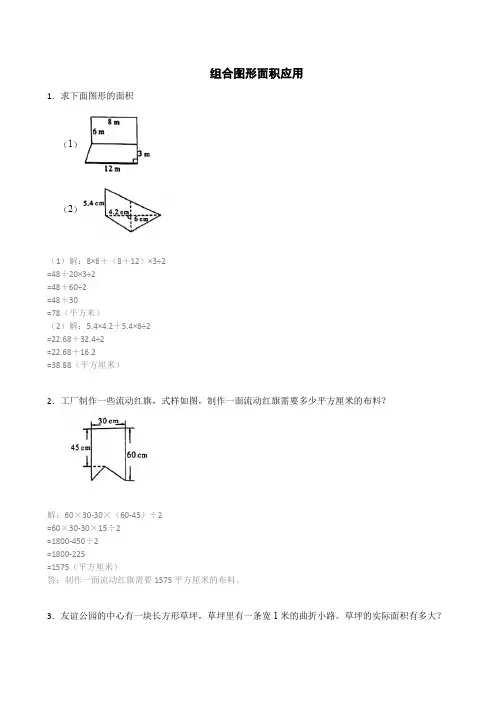
组合图形面积应用1.求下面图形的面积(1)(2)(1)解:8×6+(8+12)×3÷2=48+20×3÷2=48+60÷2=48+30=78(平方米)(2)解:5.4×4.2+5.4×6÷2=22.68+32.4÷2=22.68+16.2=38.88(平方厘米)2.工厂制作一些流动红旗,式样如图,制作一面流动红旗需要多少平方厘米的布料?解:60×30-30×(60-45)÷2=60×30-30×15÷2=1800-450÷2=1800-225=1575(平方厘米)答:制作一面流动红旗需要1575平方厘米的布料。
3.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。
草坪的实际面积有多大?解:(12-1)×(10-1)=11×9=99(平方米)答:草坪的实际面积有99平方米。
4.李叔叔家原来有一块边长12米的正方形菜地,今年他将这块菜地进行了扩建(如图中的涂色部分)。
(1)原来这块菜地的面积是多少平方米?(2)李叔叔今年扩建了多少平方米的菜地?(1)解:12×12=144(平方米)答:原来这块菜地的面积是144平方米。
(2)解:(12+7)×(12+2)-144=19×14-144=266-144=122(平方米)答:李叔叔今年扩建了122平方米的菜地。
5.求出下面图形的面积。
(1)如图,已知梯形的面积是60米2,那么,阴影部分(三角形)的面积是多少米"?(2)求出下面组合图形的面积。
(单位:厘米)(1)解:(60×2)÷(8+12)=120÷20=6(米)8×6÷2=48÷2=24(平方米)答:阴影部分(三角形)的面积是24平方米。
五年级上册数学专项拔高1.计算下面“箭头”的面积【分析】做一条辅助线将“箭头”分为一个长方形和一个三角形两部分,然后根据长方形面积=长×宽,三角形面积=底×高÷2分别计算出两部分的面积,再将这两部分面积相加即可求出“箭头”的面积。
长方形面积:18×9=162(平方厘米)三角形面积:20×15÷2=300÷2=150(平方厘米)162+150=312(平方厘米)答:“箭头”的面积是312平方厘米。
2.计算下面组合图形的面积。
【分析】组合图形的面积=长方形的长×宽+(梯形的上底+下底)×高÷2。
解:6×4+(4+6)×5÷2=24+50÷2=24+25=493.把面积是102c²的梯形分成一个平行四边形和一个三角形,计算三角形的面积。
【分析】三角形的高=梯形的高=梯形的面积×2÷上下底的和,三角形的底=梯形的下底-梯形的上底,所以三角形的面积=底×高÷2,据此代入数值作答即可。
解:102×2÷(7+10)=204÷17=12(cm)(10-7)×12÷2=3×12÷24.计算下图的面积。
①【分析】①组合图形的面积=左边梯形的面积+右边长方形的面积;其中,梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽;解:①16-10=6(厘米)(8+14)×6÷2+10×8=22×6÷2+10×8=66+80=146(平方厘米)②【分析】②平行四边形的面积=底×高;②12×8=96(平方厘米)③【分析】③梯形的面积=(上底+下底)×高÷2。
组合图形面积应用1.求图中相连的三个正方形内阴影部分的面积(单位:厘米)。
解:15-6-4=5(厘米)(5+4)×5÷2=9×5÷2=22.5(cm2)2.一块近似平行四边形的菜地,中间有一条石子路(如图)。
这块菜地的面积多少平方米?解:20×8-8×1=160-8=152(平方米)答:这块菜地的面积152平方米。
3.本次簕杜鹃花展有许多展台供市民参观,其中一个展台把展区精心布置成一个如下图所示的图形。
这个展台占地面积一共有多少平方米?解:(4+6)×(8-5)÷2+5×4=10×3÷2+5×4=15+20=35(平方米)答:这个展台占地面积一共有35平方米。
4.赵小军在一张平行四边形的硬纸板上剪下了一个三角形(如下图),剩下图形的面积是多少平方分米?解:8×6-(8-3-2)×4÷2=48-3×4÷2=48-6=42(平方分米)答:剩下图形的面积是42平方分米。
5.某农场开辟一块新的菜地(如图),一条水渠穿过这块菜地,若每平方米菜地一年可收入12元,那么这块菜地一年可收入多少元?解:18-3=15(米)23-3=20(米)(15+20)×23÷2×12=402.5×12=4830(元)答:这块菜地一年可收入3360元。
6.学校修建了一个艺术广场(平面图如下),这个艺术广场的占地面积是多少平方米?解:(15+30)×8÷2+30×20=180+600=780(平方米)答:这个艺术广场的占地面积是780平方米。
7.如图是某种植果园基地的示意图。
(1)求这个果园的面积是多少m2?(2)如果每棵果树占地10m2,这个果园共有多少棵果树?(1)解:90×40÷2+90×50=1800+4500=6300(平方米)答:这个果园的面积是6300平方米。
【重点】五年级数学“图形求面积”10法!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下——例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
人教版五年级上册《多边形的面积》要点知识及易错点解析《多边形的面积》要点知识一、公式:多边形面积公式面积公式的变式说明正方形正方形的面积=边长X边长S正=aXa=a2已知:正方形的面积,求边长长方形长方形的面积=长X宽S长=aXb已知:长方形的面积和长,求宽平行四边形平行四边形的面积=底X高S平=aXh已知:平行四边形的面积和底,求高h=S平÷a三角形三角形的面积=底X宽高÷2S三=aXh÷2已知:三角形的面积和底,求高H=S三X2÷a梯形梯形形的面积=(上底+下底)X高÷2S梯=(a+b)X2已知:梯形的面积与上下底之和,求高高=面积×2÷(上底+下底)上底=面积×2÷高-下底组合图形当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。
当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
二、平行四边形面积公式推导:剪拼、平移平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底;长方形的宽相当于平行四边形的高;长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
三、三角形面积公式推导:旋转两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2四、梯形面积公式推导:旋转两个完全一样的梯形可以拼成一个平行四边形。
平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷2五、等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍。
一、看图计算下列图形的面积。
①②
③④
3dm
5dm 8dm
25m
14m
32dm
26dm
34dm
34dm
10cm
7cm
8cm
8cm
二、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24 ④求S 阴。
平方厘米,求梯形的面积。
三、解决问题。
1、一个平行四边形的停车场,底是65米,高是24米。
平均每辆车占地15平方米,这个停车场可停车多少辆?
2、公园里有两块空地,计划分别种玫瑰和牡丹。
玫 瑰
每棵占地1m 2
每棵6元
13cm
16cm
8dm
3dm
12cm 7cm
4dm
8dm
①玫瑰园占地多少平方米?种玫瑰一共需要多少钱?
②你还能提出什么问题?
3、梯形菜园的面积是多少?
4、计算下面每个平行四边形的面积,你能发现什么?
5、竹篱笆全长84米。
这个花园面积有多大?
6、一个三角形的底是5米。
如果将底延长1米,面积就增加2平方米,原来三角形的面积是多少平方米?
7、小明家一面外墙墙皮脱落,要重新粉刷,每平方米需要用0.5千克涂料。
如
果涂料的价格是每千克10元,粉刷这面墙需要多少元?
8、每平方米放养甲鱼苗200只,可放养甲鱼苗多少只?
9、小明用红纸做直角三角形形状的小红旗,已知红纸长12分米,宽8分米,小红旗的两条直角边分别是2分米和3分米,一张红纸可做多少面小红旗?
10、①这堆钢管一共有多少根?
②这根钢管在使用前,最上面一层只有1根,而且下一层总比上一层多1根,使用前,这堆钢管一共有多少根?
30米
80米
90米
40米
2号甲鱼池平面示意。